числа фибоначчи на практике

Число Фибоначчи. Почему оно так популярно в природе?

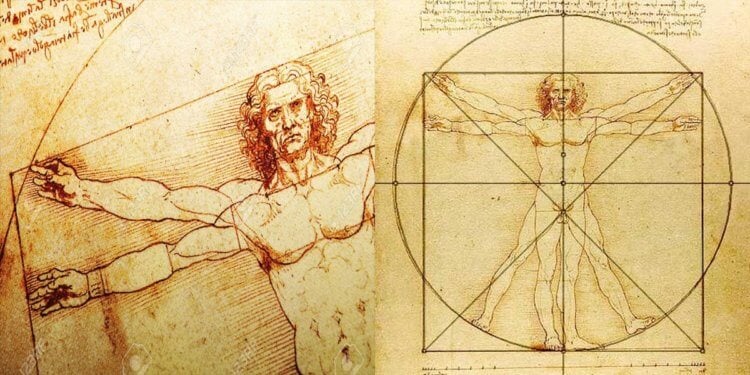
Таинственное число Фибоначчи, равное 1,618, будоражит умы ученых уже на протяжении нескольких тысячелетий. Кто-то считает это число строителем мироздания, кто-то называет его числом Бога, а кто-то, не мудрствуя лукаво, просто применяет его на практике и получает невероятные архитектурные, художественные и математические творения. Число Фибоначчи было обнаружено даже в пропорциях знаменитого «Витрувианского человека» Леонардо Да Винчи, который утверждал, что знаменитое число, пришедшее из математики, руководит всей Вселенной.

«Витрувианский человек» Леонардо да Винчи обладает идеальными пропорциями, основанными на знании свойств числа Фибоначчи

Кто такой Фибоначчи?

Леонардо Пизанский считается самым первым крупным математиком в истории средневековой Европы. Несмотря на это, свое знаменитое прозвище «Фибоначчи» ученый получил далеко не из-за своих экстраординарных математических способностей, но из-за своего везения, так как «боначчи» по-итальянски означает «удачливый». Перед тем как стать одним из самых известных математиков раннего Средневековья, Леонардо Пизанский изучал точные науки у самых продвинутых учителей своего времени, которыми считались арабы. Именно благодаря этой деятельности Фибоначчи, в Европе появились десятичная система счисления и арабские цифры, которыми мы пользуемся до сих пор.

В одном из своих самых известных трудов под названием «Liber abaci», Леонардо Пизанский приводит уникальную закономерность чисел, которые при постановке в ряд образуют линию цифр, каждая из которых является суммой двух предыдущих чисел.

Последовательность Фибоначчи

Иными словами, последовательность Фибоначчи выглядит так:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 и так далее.

Каждое число из ряда Фибоначчи, разделенное на последующее, имеет значение, стремящееся к уникальному показателю, которое составляет 1,618. Первые числа ряда Фибоначчи не дают настолько точное значение, однако по мере нарастания, соотношение постепенно выравнивается и становится все более точным.

Леонардо Пизанский — тот самый создатель числа Фибоначчи

Где используется число Фибоначчи

Из-за своего повсеместного применения в природе, золотое сечение (именно так число Фибоначчи иногда называют в искусстве и математике) считается одним из самых гармонизирующих законов мироздания, который упорядочивает структуру окружающего нас мира и направляет жизнь на развитие. Так, правило золотого сечения применяется природой для образования траекторий движения вихревых потоков в ураганах, при образовании эллиптических галактик, к которым относится и наш Млечный Путь, при «строительстве» раковины улитки или ушной раковины человека, направляет движение косяка рыб и показывает траекторию движения испуганной стаи оленей, врассыпную убегающую от хищника.

Проявление золотого сечения в природе

Эстетичность такой гармонизации мироздания воспринимается человеком, который всегда стремился улучшить окружающую его действительность, в качестве стабилизирующего природу закона. Находя золотое сечение в лице того или иного человека, мы инстинктивно воспринимаем собеседника в качестве гармоничной личности, чье развитие происходит без сбоев и нарушений. Этим можно объяснить то, почему иногда нам по непонятным причинам больше нравится одно лицо, чем другое. Оказывается, о наших возможных симпатиях позаботилась природа!

Как вы считаете, является ли повсеместное применение числа Фибоначчи в природе совпадением или свидетельством наличия некоего вселенского разума? Давайте попробуем обсудить этот вопрос в нашем Telegram-чате.

Наиболее распространенное определение золотого сечения гласит, что меньшая часть так относится к большей, как большая часть относится ко всему целому. Уникальное правило встречается во всех областях природы, науки и искусства, позволив некоторым именитым исследователям Средних Веков сделать предположение, что три основные части золотого сечения олицетворяют собой христианских Отца, Сына и Святого Духа.

Правилу золотого сечения следуют даже галактики. Наш Млечный Путь в этом плане не является исключением

Что такое золотое сечение

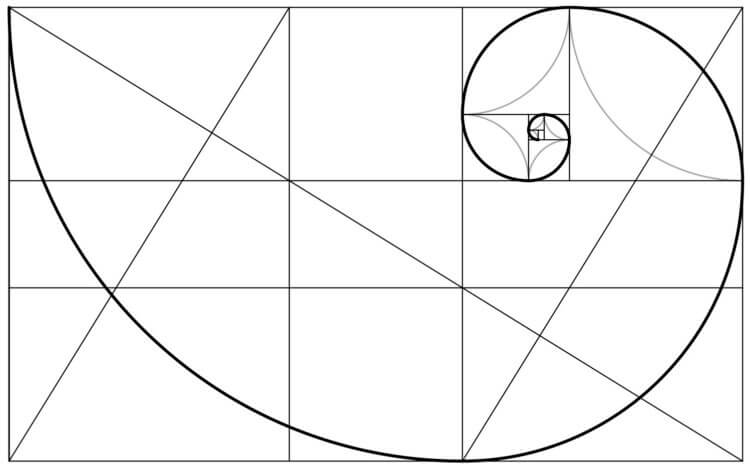
С точки зрения математики, золотое сечение представляет собой некую идеальную пропорцию, к которой каким-то образом стремится все живое и неживое в природе.

Так выглядит «золотое сечение»

Используя основные принципы ряда Фибоначчи, растут семечки в центре подсолнуха, движется спираль ДНК, был построен Парфенон и написана самая знаменитая картина в мире — «Джоконда» Леонардо Да Винчи.

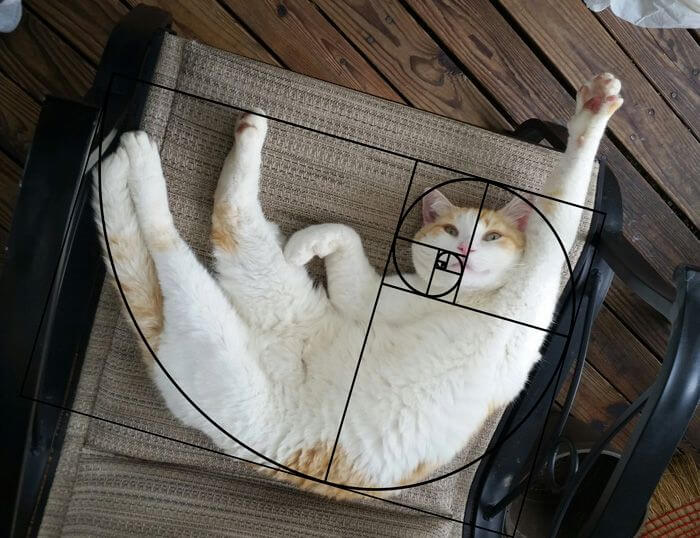
Даже коты неосознанно (хотя, кто знает?) следуют принципу золотого сечения, становясь любимцами большей части населения планеты

Есть ли в природе гармония? Несомненно, есть. А ее доказательством служит число Фибоначчи, происхождение которого нам еще только предстоит отыскать.

Новости, статьи и анонсы публикаций

Свободное общение и обсуждение материалов

Китай строит самый большой радиотелескоп на Земле. И это строительство в буквальном смысле потребовало человеческих жертв. Нет, к счастью, речь идет не о чел…

«В Долине мы сделали невероятное открытие; великолепная гробница с нетронутыми печатями останется такой же к вашему прибытию с поздравлениями», — такое сообщ…

Некоторые типы сверхновых, или взрывающихся звезд, более распространены, чем считалось раньше, обнаружили астрономы Университета Аризоны. Результаты были опу…

Источник

5 способов вычисления чисел Фибоначчи: реализация и сравнение

Введение

Программистам числа Фибоначчи должны уже поднадоесть. Примеры их вычисления используются везде. Всё от того, что эти числа предоставляют простейший пример рекурсии. А ещё они являются хорошим примером динамического программирования. Но надо ли вычислять их так в реальном проекте? Не надо. Ни рекурсия, ни динамическое программирование не являются идеальными вариантами. И не замкнутая формула, использующая числа с плавающей запятой. Сейчас я расскажу, как правильно. Но сначала пройдёмся по всем известным вариантам решения.

Код предназначен для Python 3, хотя должен идти и на Python 2.

Для начала – напомню определение:

Замкнутая формула

Решаем квадратное уравнение:

Откуда и растёт «золотое сечение» ϕ=(1+√5)/2. Подставив исходные значения и проделав ещё вычисления, мы получаем:

что и используем для вычисления F_n.

Хорошее:
Быстро и просто для малых n
Плохое:
Требуются операции с плавающей запятой. Для больших n потребуется большая точность.
Злое:
Использование комплексных чисел для вычисления F_n красиво с математической точки зрения, но уродливо — с компьютерной.

Рекурсия

Самое очевидное решение, которое вы уже много раз видели – скорее всего, в качестве примера того, что такое рекурсия. Повторю его ещё раз, для полноты. В Python её можно записать в одну строку:

Хорошее:
Очень простая реализация, повторяющая математическое определение
Плохое:
Экспоненциальное время выполнения. Для больших n очень медленно
Злое:
Переполнение стека

Запоминание

У решения с рекурсией есть большая проблема: пересекающиеся вычисления. Когда вызывается fib(n), то подсчитываются fib(n-1) и fib(n-2). Но когда считается fib(n-1), она снова независимо подсчитает fib(n-2) – то есть, fib(n-2) подсчитается дважды. Если продолжить рассуждения, будет видно, что fib(n-3) будет подсчитана трижды, и т.д. Слишком много пересечений.

Поэтому надо просто запоминать результаты, чтобы не подсчитывать их снова. Время и память у этого решения расходуются линейным образом. В решении я использую словарь, но можно было бы использовать и простой массив.

(В Python это можно также сделать при помощи декоратора, functools.lru_cache.)

Хорошее:
Просто превратить рекурсию в решение с запоминанием. Превращает экспоненциальное время выполнение в линейное, для чего тратит больше памяти.
Плохое:
Тратит много памяти
Злое:
Возможно переполнение стека, как и у рекурсии

Динамическое программирование

После решения с запоминанием становится понятно, что нам нужны не все предыдущие результаты, а только два последних. Кроме этого, вместо того, чтобы начинать с fib(n) и идти назад, можно начать с fib(0) и идти вперёд. У следующего кода линейное время выполнение, а использование памяти – фиксированное. На практике скорость решения будет ещё выше, поскольку тут отсутствуют рекурсивные вызовы функций и связанная с этим работа. И код выглядит проще.

Это решение часто приводится в качестве примера динамического программирования.

Хорошее:
Быстро работает для малых n, простой код
Плохое:
Всё ещё линейное время выполнения
Злое:
Да особо ничего.

Матричная алгебра

И, наконец, наименее освещаемое, но наиболее правильное решение, грамотно использующее как время, так и память. Его также можно расширить на любую гомогенную линейную последовательность. Идея в использовании матриц. Достаточно просто видеть, что

А обобщение этого говорит о том, что

Два значения для x, полученных нами ранее, из которых одно представляло собою золотое сечение, являются собственными значениями матрицы. Поэтому, ещё одним способом вывода замкнутой формулы является использование матричного уравнения и линейной алгебры.

Так чем же полезна такая формулировка? Тем, что возведение в степень можно произвести за логарифмическое время. Это делается через возведения в квадрат. Суть в том, что

где первое выражение используется для чётных A, второе для нечётных. Осталось только организовать перемножения матриц, и всё готово. Получается следующий код. Я организовал рекурсивную реализацию pow, поскольку её проще понять. Итеративную версию смотрите тут.

Хорошее:
Фиксированный объём памяти, логарифмическое время
Плохое:
Код посложнее
Злое:
Приходится работать с матрицами, хотя они не так уж и плохи

Сравнение быстродействия

Сравнивать стоит только вариант динамического программирования и матрицы. Если сравнивать их по количеству знаков в числе n, то получится, что матричное решение линейно, а решение с динамическим программированием – экспоненциально. Практический пример – вычисление fib(10 ** 6), числа, у которого будет больше двухсот тысяч знаков.

n = 10 ** 6
Вычисляем fib_matrix: у fib(n) всего 208988 цифр, расчёт занял 0.24993 секунд.
Вычисляем fib_dynamic: у fib(n) всего 208988 цифр, расчёт занял 11.83377 секунд.

Теоретические замечания

Не напрямую касаясь приведённого выше кода, данное замечание всё-таки имеет определённый интерес. Рассмотрим следующий граф:

Подсчитаем количество путей длины n от A до B. Например, для n = 1 у нас есть один путь, 1. Для n = 2 у нас опять есть один путь, 01. Для n = 3 у нас есть два пути, 001 и 101. Довольно просто можно показать, что количество путей длины n от А до В равно в точности F_n. Записав матрицу смежности для графа, мы получим такую же матрицу, которая была описана выше. Это известный результат из теории графов, что при заданной матрице смежности А, вхождения в А n — это количество путей длины n в графе (одна из задач, упоминавшихся в фильме «Умница Уилл Хантинг»).

Почему на рёбрах стоят такие обозначения? Оказывается, что при рассмотрении бесконечной последовательности символов на бесконечной в обе стороны последовательности путей на графе, вы получите нечто под названием «подсдвиги конечного типа», представляющее собой тип системы символической динамики. Конкретно этот подсдвиг конечного типа известен, как «сдвиг золотого сечения», и задаётся набором «запрещённых слов» <11>. Иными словами, мы получим бесконечные в обе стороны двоичные последовательности и никакие пары из них не будут смежными. Топологическая энтропия этой динамической системы равна золотому сечению ϕ. Интересно, как это число периодически появляется в разных областях математики.

Источник

Золотое сечение и числа Фибоначчи

Человек стремится к знаниям, пытается изучить мир, который его окружает. В процессе наблюдений появляются многочисленные вопросы, на которые, соответственно, требуется найти ответы. Человек ищет эти ответы, а находя их, появляются другие вопросы.

Оказывается, закономерность явлений природы, строение и многообразие живых организмов на нашей планете, всё, что нас окружает, поражая воображение своей гармонией и упорядоченностью, законы мироздания, движение человеческой мысли и достижения науки – всё это можно объяснить последовательностью Фибоначчи.

Леонардо был рожден в Пизе. Впоследствии получил прозвище Фибоначчи, что означает «хорошо рожденный сын». Когда Леонардо жил со своим отцом в странах Северной Африки, он изучал математику с арабскими учителями. Получив весь необходимый материал, он создал собственную книгу – «Книгу абака». Именно этот человек становится первым средневековым учёным, познакомившим Европу с арабской системой счисления, которой мы пользуемся всю нашу жизнь[1].

Основная задача, поясняющая возникновение ряда чисел Фибоначчи – задача о кроликах. Вопрос задачи звучит так: «Сколько пар кроликов в один год рождается от одной пары?». К задаче дано пояснение, что пара через месяц рождает ещё одну пару, а по природе кролики начинают объектом рождать потомство на второй месяц после своего рождения. Автор даёт нам решение задачи. Получается, что в первый месяц первая пара родит ещё одну. Во второй месяц первая пара родит ещё одну – будет три пары. В третий месяц родят две пары — изначально данная и рождённая в первый месяц. Получается пять пар. И так далее. Используя такую же логику в рассуждении, мы получим, что в четвёртый месяц будет 8 пар, в пятый– 13, в шестой – 21, в седьмой 34, в восьмой — 55, в девятый — 89, в десятый 144, в одиннадцатый – 233, в двенадцатый — 377[2](рис. 1).

Из этой задачи и можно вывести саму последовательность чисел Фибоначчи: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,… В основе этой последовательности лежит алгоритм: начиная с «1, 1» следующим числом будет сумма двух предыдущих чисел. Разделив любой член данной последовательности на член, который стоит перед ним, мы получим величину, называемую «пропорцией Золотого сечения» — примерно 1, 618[3].

В эпоху Возрождения художники открыли некие зрительные центры, которые, влияя на психику человека, невольно приковывают наше внимание. Данные точки не зависят от формата картины. Их всего четыре, они делят картину в пропорциях Золотого сечения- примерно 3/8 и 5/8 (рис.2).

Для того чтобы привлечь внимание зрителя к определенному элементу картины, необходимо совместить его с одним из зрительных центров. Данное открытие назвали «золотое сечение картины»[4].

Правило золотого сечения используется в стоматологии, именно они используются при художественной реставрации зубов, их восстановлении. Рассмотрим эстетическое восстановление передних зубов, фронтального зубного ряда (рис. 3)[5].

Золотые пропорции включают в себя такие моменты:

— как ширина верхнего переднего зуба относится к ширине нижнего;

— как соотносятся между собой по ширине:

2 резца в нижнем фронтальном ряду;

двое резцов в верхнем ряду;

— какое имеется расстояние между премолярами и т.д.

Так же правило золотого сечения используется в косметологии и пластической хирургии. У людей с красивыми лицами существует идеальная пропорция между расстояниями от медиального угла глаза до крыла носа и от крыла носа до подбородка. Это явление называется «динамической симметрией» или «динамическим равновесием».

Расстояние от линии смыкания губ до крыльев носа пропорционально расстоянию от линии губ до низшей точки подбородка в соотношении 1: 1,618. Ещё существует множество соотношений на лице, которые представлены на рисунке 4[6].

Числа Фибоначчи и Золотое сечение чтобы также используется и в психологии. Например, чтобы выяснить, как развивается механизм творчества, В.В. Клименко воспользовался математикой, а именно законами чисел Фибоначчи и пропорцией «золотого сечения» — законами природы и жизни человека. Если развернуть в ряд числа Фибоначчи, то получим: 1,1, 2, 3, 5, 8, 13, 21, 34, 55, 89 и т.д. Отношение между числами Фибоначчи составляет 0,618. Развитие человека также происходит соответственно данной пропорции и подчиняется закону ее чисел, разделяя нашу жизнь на этапы с теми или иными доминантами механизма творчества [7].

Числа Фибоначчи делят нашу жизнь на этапы по количеству прожитых лет:

• 0 —начало отсчета — ребёнок родился. У него еще отсутствуют не только психомоторика, мышление, чувства, воображение, но и оперативный энергопотенциал. Он — начало новой жизни, новой гармонии;

• 1 — ребенок овладел ходьбой и осваивает ближайшее окружение;

• 2 — понимает речь и действует, пользуясь словесными указаниями;

• 3 — действует посредством слова, задаёт вопросы;

• 5 — «возраст грации» — гармония психомоторики, памяти, воображения и чувств, которые уже позволяют ребёнку охватить мир во всей его целостности;

• 8 — на передний план выходят чувства. Им служит воображение, а мышление силами своей критичности направлено на поддержку внутренней и внешней гармонии…

Закономерность явлений природы, строение и многообразие живых организмов на нашей планете, всё, что нас окружает, поражая воображение своей гармонией и упорядоченностью, законы мироздания, движение человеческой мысли и достижения науки – всё это можно объяснить последовательностью Фибоначчи.

В заключении отмечу, что данная работа является законченным исследованием и при этом имеет ряд перспектив. В дальнейшем возможно исследовать как числа Фибоначчи используются в биологии, химии, как это можно использовать и применять на практике в бытовых условиях.

1. Воробьев Н.Н. Числа Фибоначчи. – 5-е изд. – М.: Наука, 1978 – 144с.

Источник

Секреты Фибоначчи, о которых вы раньше не знали

Благодаря стараниям Леонардо Фибоначчи, в 13 веке мир увидел числовую последовательность, в которой каждое следующее число равнялось сумме двух предыдущих. Разница между числами составляет 1,618. Впоследствии числовая последовательность Фибоначчи получила название «золотое сечение».

Все в природе, и даже человеческое тело, представляет собой золотое сечение. Об этом написано достаточно книг, поэтому сейчас я не буду вдаваться в подробности. Целью написания этой статьи было обратить внимание трейдеров на эффективные методы применения чисел Фибоначчи в торговле на финансовых рынках. Речь пойдет о довольно простых для понимания стратегиях, однако их использование позволит добиться стабильного положительного результата в управлении капиталом.

Нанесение сетки

Линии золотого сечения являются популярным аналитическим инструментом, поэтому встречаются в любом терминале. В торговых платформах предусмотрено несколько технических инструментов, основанных на числовой последовательности Фибоначчи (зоны, веер и другие), но сегодня мы остановимся исключительно на линиях, как на самом эффективном из них.

Для нанесения линий Фибоначчи на график в MetaTrader потребуется открыть вкладку «Вставка» в верхнем меню терминала, выбрать пункт «Фибоначчи» и «Линии». Сетку следует растягивать от локального максимума к минимуму сверху вниз, или от минимума к максимуму снизу вверх. В результате должно получиться примерно следующее:

На скриншоте красным маркером отмечены точки (локальные уровни), на которые следует ориентироваться при нанесении сетки. Грубо говоря, это границы локального тренда. Наиболее значимыми в линиях Фибоначчи являются 100.0 и 0.0. Закрепление графика ниже/ выше упомянутых значений будет сигналом к формированию тренда. Движения цены в диапазоне между линиями 38,2 и 61,8 указывают на флэт. Во многих курсах по Форекс-трейдингу рекомендуют воздержаться от открытия ордеров в таких случаях.

Внимание! Большинство начинающих трейдеров стремятся найти или разработать стратегию, которая бы позволила зарабатывать на каждом трендовом движении. Практика опытных участников торгов свидетельствует о том, что это невозможно. В лучшем случае трейдер сможет заработать на 20% от тренда. На это следует ориентироваться при разработке торгового плана. Практика еще показывает, что стремление извлечь максимум прибыли из движений графика вопреки правилам применяемой стратегии приводит к значительным убыткам.

Зарабатываем на ГЭПах с помощью линий Фибоначчи

ГЭП – разрыв на ценовом графике, который, по статистике, отрабатывается в 70% случаев (зависит от выбранной валютной пары). Стратегия торговли предельно проста. Достаточно дождаться открытия торгов в ночь с воскресенья на понедельник, после чего, в случае формирования разрыва, открыть ордер с целевым значением в точке закрытия рынка в ночь пятницы.

Все выглядит просто, а результативность такого подхода к торговле несложно проверить на истории котировок. Однако при реальной торговле трейдеры сталкиваются с рядом сюрпризов:

Применение уровней Фибоначчи в торговле по гэпам позволит не только устранить упомянутые выше неприятности, но и значительно улучшить финансовый результат. Для этого потребуется растянуть сетку таким образом, чтобы уровни 38,2 и 61,8 соответствовали границам ценового разрыва. Например:

Если график преодолел уровень 23,6о Фибоначчи, то он продолжит движение в этом направлении в 80% случаев. Это правило работает только с высоколиквидными активами (EUR/USD, GBP/USD, JPY/USD и другими). Средняя дневная волатильность валютной пары не должна быть менее 150 пунктов.

На представленном выше примере ГЭП был отработан частично. Открывать ордер целесообразно тогда, когда график преодолеет небольшое расстояние в направлении ценового разрыва, после чего повторно вернется к границе (61,8 или 38,2, в зависимости от тренда). Проведенные с ориентиром на ГЭП линии допустимо использовать даже после отработки ценового разрыва и открывать новые сделки в случае их преодоления.

Важно! Для торговли по гэпам с применением уровней Фибоначчи открытие ордера целесообразно рассматривать только в том случае, если диапазон разрыва более 20 пунктов. В остальных случаях ГЭП можно использовать для прогнозирования дальнейшей тенденции ценообразования. На графиках H4 с помощью этого подхода возможно благодаря ценовому разрыву составить торговый план на неделю вперед, обозначив важные локальные уровни.

Рассмотрим еще один пример:

Внимание! Остерегайтесь ложных пробоев уровней. Важно всегда дожидаться закрытия сигнальной свечи и закрепления графика в новой плоскости. В противном случае в торговле будет большое число ложных сделок, что по итогу месяца/года приведет к убыткам.

Парабола 38,2 и 61,8

Ведение торговли в этом диапазоне не рекомендуется трейдерам, а очень зря. Ведь главное – правильно выбрать валютную пару. Если рассмотренный выше метод торговли по сетке «золотого сечения» универсален (может применяться на любом таймфрейме и с любым производным активом), то в охоте за параболой Фибоначчи мы будем обращать внимание только на трендовые финансовые инструменты (AUD/USD, GBP/USD и прочие).

Правила торговли просты:

Внимание! Более опытные трейдеры сейчас могли заметить, что потенциальный убыток превышает возможную прибыль. На практике это компенсируется тем, что сделки по Stop Loss закрываются крайне редко.

Теперь рассмотрим пару примеров:

В кружки обведены точки, взятые за основу при растягивании сетки Фибоначчи. Стрелка указывает точку входа и направление ордера. Третьим кругом отмечена точка закрытия сделки с фиксированием прибыли.

Важно! Ордера лучше открывать вручную. Рыночный шум никто не отменял даже на старших таймфреймах, поэтому ложные пробои, увы, не редкость.

Обратите внимание, что в этом примере точка открытия ордера немного ниже нужного уровня, поскольку именно на этом моменте график закрепился за линией 23,6 по Фибоначчи. Как видите, сделка закрылась по Take Profit.

Не стоит забывать о возможности частичного закрытия ордеров, что может очень пригодиться в ходе торговли по Фибоначчи сторонникам более агрессивных стратегий.

Важно! Уровни Фибоначчи можно назвать отличным фундаментом для создания собственной стратегии в силу их универсальности. Практически все успешные трейдеры используют этот инструмент в своей торговле, а инвестор Джек Сингер даже умудрился с помощью золотого сечения подбирать активы (включая счета ПАММ) для пассивного заработка.

Источник