cost function машинное обучение

Представление модели и функция стоимости Машинное обучение

Дата публикации Nov 13, 2019

Итак, я начал делать популярный курс машинного обучения от Coursera. И подумал, а почему бы не поделиться тем, что я изучаю? Итак, сегодня я собираюсь поговорить о двух фундаментальных темах машинного обучения.

Представление модели:

Гипотеза обычно представлена

Здесь theta1 и theta2 являются параметрами.

Давайте представим нашу гипотезу на примере со случайными значениями для theta1, theta2 и x:

давайте посмотрим на другой пример:

Функция стоимости:

Примечание: среднее значение уменьшено вдвое (1/2) для удобства вычисления градиентного спуска, поскольку производный член функции квадрата отменит член (1/2).

Мы хотим получить лучшую возможную линию. Когда среднеквадратические вертикальные расстояния рассеянных точек от линии будут минимальными, тогда мы получим наилучшую возможную линию. Давайте посмотрим примеры, где наша функция стоимости будет 0, и у нас будет лучшая возможная строка:

Когда theta1 = 1, мы получаем наклон 1, а наша функция стоимости равна 0.

Теперь давайте предположим, что theta1 = 0.5

Мы можем видеть, что это увеличивает нашу функцию стоимости до 0,5833

Теперь мы будем строить больше значений J (theta1):

отказЯ просто делюсь тем, что узнал из известного курса Эндрю Нг по машинному обучению. В следующей статье я буду говорить о градиентном спуске.

Прошу прощения за мой худший (!) Почерк.

Источник

Функция потерь (Loss Function)

Функция потерь (Loss Function, Cost Function, Error Function; J) – фрагмент программного кода, который используется для оптимизации Алгоритма (Algorithm) Машинного обучения (ML). Значение, вычисленное такой функцией, называется «потерей».

Функция (Function) потерь может дать бо́льшую практическую гибкость вашим Нейронным сетям (Neural Network) и будет определять, как именно выходные данные связаны с исходными.

Нейронные сети могут выполнять несколько задач: от прогнозирования непрерывных значений, таких как ежемесячные расходы, до Бинарной классификации (Binary Classification) на кошек и собак. Для каждой отдельной задачи потребуются разные типы функций, поскольку выходной формат индивидуален.

С очень упрощенной точки зрения Loss Function может быть определена как функция, которая принимает два параметра:

Эта функция, по сути, вычислит, насколько хорошо работает наша модель, сравнив то, что модель прогнозирует, с фактическим значением, которое она должна выдает. Если Y_pred очень далеко от Yi, значение потерь будет очень высоким. Однако, если оба значения почти одинаковы, значение потерь будет очень низким. Следовательно, нам нужно сохранить функцию потерь, которая может эффективно наказывать модель, пока та обучается на Тренировочных данных (Train Data).

Этот сценарий в чем-то аналогичен подготовке к экзаменам. Если кто-то плохо сдает экзамен, мы можем сказать, что потеря очень высока, и этому человеку придется многое изменить внутри себя, чтобы в следующий раз получить лучшую оценку. Однако, если экзамен пройдет хорошо, студент может вести себя подобным образом и в следующий раз.

Теперь давайте рассмотрим классификацию как задачу и поймем, как в этом случае работает функция потерь.

Классификационные потери

Когда нейронная сеть пытается предсказать дискретное значение, мы рассматриваем это как модель классификации. Это может быть сеть, пытающаяся предсказать, какое животное присутствует на изображении, или является ли электронное письмо спамом. Сначала давайте посмотрим, как представлены выходные данные классификационной нейронной сети.

Выходной формат данных нейросети бинарной классификации

Количество узлов выходного слоя будет зависеть от количества классов, присутствующих в данных. Каждый узел будет представлять один класс. Значение каждого выходного узла по существу представляет вероятность того, что этот класс является правильным.

Как только мы получим вероятности всех различных классов, рассмотрим тот, что имеет наибольшую вероятность. Посмотрим, как выполняется двоичная классификация.

Бинарная классификация

В двоичной классификации на выходном слое будет только один узел. Чтобы получить результат в формате вероятности, нам нужно применить Функцию активации (Activation Function). Поскольку для вероятности требуется значение от 0 до 1, мы будем использовать Сигмоид (Sigmoid), которая приведет любое реальное значение к диапазону значений от 0 до 1.

Визуализация преобразования значения сигмоидом

По мере того, как входные реальные данные становятся больше и стремятся к плюс бесконечности, выходные данные сигмоида будут стремиться к единице. А когда на входе значения становятся меньше и стремятся к отрицательной бесконечности, на выходе числа будут стремиться к нулю. Теперь мы гарантированно получаем значение от 0 до 1, и это именно то, что нам нужно, поскольку нам нужны вероятности.

Если выход выше 0,5 (вероятность 50%), мы будем считать, что он попадает в положительный класс, а если он ниже 0,5, мы будем считать, что он попадает в отрицательный класс. Например, если мы обучаем нейросеть для классификации кошек и собак, мы можем назначить собакам положительный класс, и выходное значение в наборе данных для собак будет равно 1, аналогично кошкам будет назначен отрицательный класс, а выходное значение для кошек будет быть 0.

Функция потерь, которую мы используем для двоичной классификации, называется Двоичной перекрестной энтропией (BCE). Эта функция эффективно наказывает нейронную сеть за Ошибки (Error) двоичной классификации. Давайте посмотрим, как она выглядит.

Графики потери бинарной кросс-энтропии

Как видите, есть две отдельные функции, по одной для каждого значения Y. Когда нам нужно предсказать положительный класс (Y = 1), мы будем использовать следующую формулу:

И когда нам нужно предсказать отрицательный класс (Y = 0), мы будем использовать немного трансформированный аналог:

Для первой функции, когда Y_pred равно 1, потеря равна 0, что имеет смысл, потому что Y_pred точно такое же, как Y. Когда значение Y_pred становится ближе к 0, мы можем наблюдать, как значение потери сильно увеличивается. Когда же Y_pred становится равным 0, потеря стремится к бесконечности. Это происходит, потому что с точки зрения классификации, 0 и 1 – полярные противоположности: каждый из них представляет совершенно разные классы. Поэтому, когда Y_pred равно 0, а Y равно 1, потери должны быть очень высокими, чтобы сеть могла более эффективно распознавать свои ошибки.

Сравнение потерь двоичной классификации

Полиномиальная классификация

Полиномиальная классификация (Multiclass Classification) подходит, когда нам нужно, чтобы наша модель каждый раз предсказывала один возможный класс. Теперь, поскольку мы все еще имеем дело с вероятностями, имеет смысл просто применить сигмоид ко всем выходным узлам, чтобы мы получали значения от 0 до 1 для всех выходных значений, но здесь кроется проблема. Когда мы рассматриваем вероятности для нескольких классов, нам необходимо убедиться, что сумма всех индивидуальных вероятностей равна единице, поскольку именно так определяется вероятность. Применение сигмоида не гарантирует, что сумма всегда равна единице, поэтому нам нужно использовать другую функцию активации.

В данном случае мы используем функцию активации Softmax. Эта функция гарантирует, что все выходные узлы имеют значения от 0 до 1, а сумма всех значений выходных узлов всегда равна 1. Вычисляется с помощью формулы:

Как видите, мы просто передаем все значения в экспоненциальную функцию. После этого, чтобы убедиться, что все они находятся в диапазоне от 0 до 1 и сумма всех выходных значений равна 1, мы просто делим каждую экспоненту на сумму экспонент.

Итак, почему мы должны передавать каждое значение через экспоненту перед их нормализацией? Почему мы не можем просто нормализовать сами значения? Это связано с тем, что цель Softmax – убедиться, что одно значение очень высокое (близко к 1), а все остальные значения очень низкие (близко к 0). Softmax использует экспоненту, чтобы убедиться, что это произойдет. А затем мы нормализуем результат, потому что нам нужны вероятности.

Теперь, когда наши выходные данные имеют правильный формат, давайте посмотрим, как мы настраиваем для этого функцию потерь. Хорошо то, что функция потерь по сути такая же, как у двоичной классификации. Мы просто применим Логарифмическую потерю (Log Loss) к каждому выходному узлу по отношению к его соответствующему целевому значению, а затем найдем сумму этих значений по всем выходным узлам.

Категориальная кросс-энтропия

Эта потеря называется категориальной Кросс-энтропией (Cross Entropy). Теперь перейдем к частному случаю классификации, называемому многозначной классификацией.

Классификация по нескольким меткам

Классификация по нескольким меткам (MLC) выполняется, когда нашей модели необходимо предсказать несколько классов в качестве выходных данных. Например, мы тренируем нейронную сеть, чтобы предсказывать ингредиенты, присутствующие на изображении какой-то еды. Нам нужно будет предсказать несколько ингредиентов, поэтому в Y будет несколько единиц.

Для этого мы не можем использовать Softmax, потому что он всегда заставляет только один класс «становиться единицей», а другие классы приводит к нулю. Вместо этого мы можем просто сохранить сигмоид на всех значениях выходных узлов, поскольку пытаемся предсказать индивидуальную вероятность каждого класса.

Что касается потерь, мы можем напрямую использовать логарифмические потери на каждом узле и суммировать их, аналогично тому, что мы делали в мультиклассовой классификации.

Теперь, когда мы рассмотрели классификацию, перейдем к регрессии.

Потеря регрессии

В Регрессии (Regression) наша модель пытается предсказать непрерывное значение, например, цены на жилье или возраст человека. Наша нейронная сеть будет иметь один выходной узел для каждого непрерывного значения, которое мы пытаемся предсказать. Потери регрессии рассчитываются путем прямого сравнения выходного и истинного значения.

Самая популярная функция потерь, которую мы используем для регрессионных моделей, – это Среднеквадратическая ошибка (MSE). Здесь мы просто вычисляем квадрат разницы между Y и Y_Pred и усредняем полученное значение.

Источник

Machine learning fundamentals (I): Cost functions and gradient descent

**This is part one of a series on machine learning fundamentals. ML fundamentals (II): Neural Networks can be found at https://towardsdatascience.com/machine-learning-fundamentals-ii-neural-networks-f1e7b2cb3eef**

Nov 27, 2017 · 8 min read

In this post I’ll use a simple linear regression model to explain two machine learning (ML) fundamentals; (1) cost functions and; (2) gradient descent. The linear regression isn’t the most powerful model in the ML tool kit, but due to its familiarity and interpretability, it is still in widespread use in research and industry. Simply, linear regression is used to estimate linear relationships between continuous or/and categorical data and a continuous output variable — you can see an example of this in a previous post of mine https://conorsdatablog.wordpress.com/2017/09/02/a-quick-and-tidy-data-analysis/.

As I go thro u gh this post, I’ll use X and y to refer to variables. If you prefer something more concrete (as I often do), you can imagine that y is sales, X is advertising spend and we want to estimate how advertising spend impacts sales. Visually, I’ll show how a linear regression learns the best line to fit through this data:

What does the machine learn?

One question that people often have when getting started in ML is:

“What does the machine (i.e. the statistical model) actually learn?”

This will vary from model to model, but in simple terms the model learns a function f such that f( X) maps to y. Put differentl y, the model learns how to take X (i.e. features, or, more traditionally, independent variable(s)) in order to predict y (the target, response or more traditionally the dependent variable).

In the case of the simple linear regression ( y

b0 + b1 * X where X is one column/variable) the model “learns” (read: estimates) two parameters;

The bias is the level of y when X is 0 (i.e. the value of sales when advertising spend is 0) and the slope is the rate of predicted increase or decrease in y for each unit increase in X (i.e. how much do sales increase per pound spent on advertising). Both parameters are scalars (single values).

Once the model learns these parameters they can be used to compute estimated values of y given new values of X. In other words, you can use these learned parameters to predict values of y when you don’t know what y is — hey presto, a predictive model!

Learning parameters: Cost functions

There are several ways to learn the parameters of a LR model, I will focus on the approach that best illustrates statistical learning; minimising a cost function.

Remember that in ML, the focus is on learning from data. This is perhaps better illustrated using a simple analogy. As children we typically learn what is “right” or “good” behaviour by being told NOT to do things or being punished for having done something we shouldn’t. For example, you can imagine a four year-old sitting by a fire to keep warm, but not knowing the danger of fire, she puts her finger into it and gets burned. The next time she sits by the fire, she doesn’t get burned, but she sits too close, gets too hot and has to move away. The third time she sits by the fire she finds the distance that keeps her warm without exposing her to any danger. In other words, through experience and feedback (getting burned, then getting too hot) the kid learns the optimal distance to sit from the fire. The heat from the fire in this example acts as a cost function — it helps the learner to correct / change behaviour to minimize mistakes.

In ML, cost functions are used to estimate how badly models are performing. Put simply, a cost function is a measure of how wrong the model is in terms of its ability to estimate the relationship between X and y. This is typically expressed as a difference or distance between the predicted value and the actual value. The cost function (you may also see this referred to as loss or error.) can be estimated by iteratively running the model to compare estimated predictions against “ground truth” — the known values of y.

The objective of a ML model, therefore, is to find parameters, weights or a structure that minimises the cost function.

Minimizing the cost function: Gradient descent

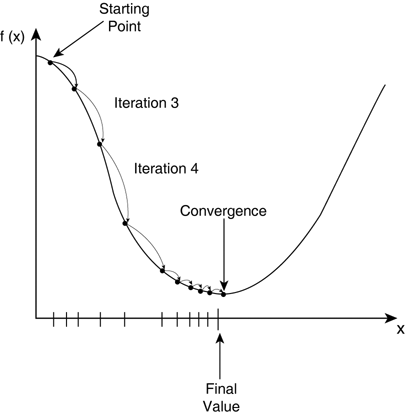
Now that we know that models learn by minimizing a cost function, you may naturally wonder how the cost function is minimized — enter gradient descent. Gradient descent is an efficient optimization algorithm that attempts to find a local or global minima of a function.

Gradient descent enables a model to learn the gradient or direction that the model should take in order to reduce errors (differences between actual y and predicted y). Direction in the simple linear regression example refers to how the model parameters b0 and b1 should be tweaked or corrected to further reduce the cost function. As the model iterates, it gradually converges towards a minimum where further tweaks to the parameters produce little or zero changes in the loss — also referred to as convergence.

Observing learning in a linear regression model

To observe learning in a linear regression, I will set the parameters b0 and b1 and will use a model to learn these parameters from the data. In other words, we know the ground truth of the relationship between X and y and can observe the model learning this relationship through iterative correction of the parameters in response to a cost (note: the code below is written in R).

Here I define the bias and slope (equal to 4 and 3.5 respectively). I also add a column of ones to X (for the purposes of enabling matrix multiplication). I also add some Gaussian noise to y to mask the true parameters — i.e. create errors that are purely random. Now we have a dataframe with two variables, X and y, that appear to have a positive linear trend (as X increases values of y increase).

Next I define the learning rate — this controls the size of the steps taken by each gradient. If this is too big, the model might miss the local minimum of the function. If it too small, the model will take a long time to converge (copy the code and try this out for yourself!). Theta stores the parameters b0 and b1, which are initialized with random values (I have set these these both to 20, which is suitably far away from the true parameters). The n_iterations value controls how many times the model will iterate and update values. That is, how many times the model will make predictions, calculate the cost and gradients and update the weights. Finally, I create some placeholders to catch the values of b0, b1 and the mean squared error (MSE) upon each iteration of the model (creating these placeholders avoids iteratively growing a vector, which is very inefficient in R).

The MSE in this case is the cost function. It is simply the mean of the squared differences between predicted y and actual y (i.e. the residuals)

Now, we run the loop. On each iteration the model will predict y given the values in theta, calculate the residuals, and then apply gradient descent to estimate corrective gradients, then will update the values of theta using these gradients — this process is repeated 100 times. When the loop is finished, I create a dataframe to store the learned parameters and loss per iteration.

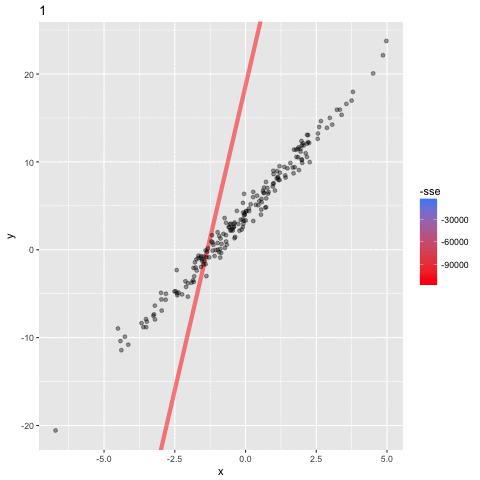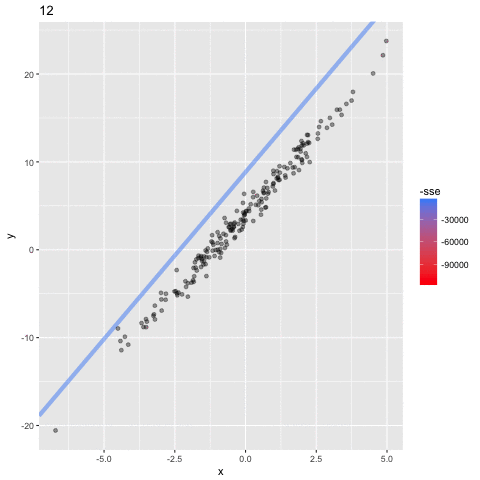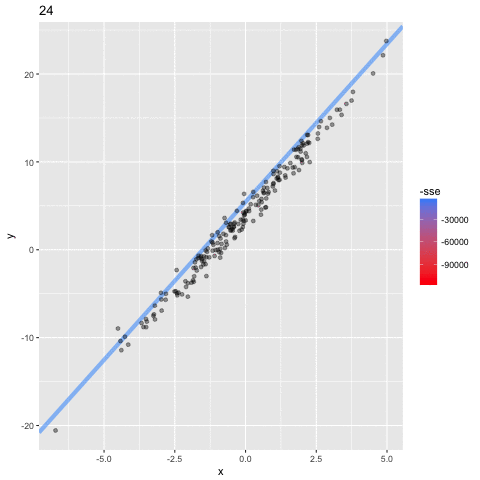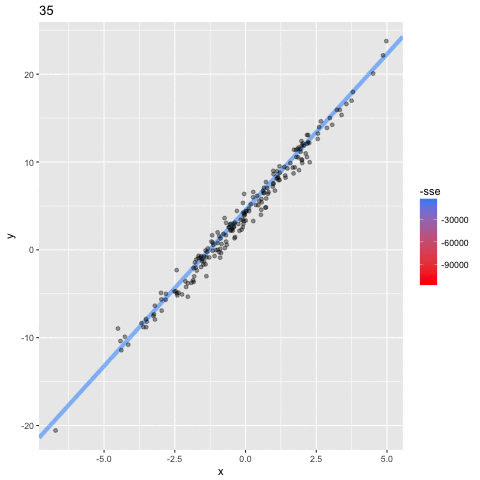
When the iterations have completed we can plot the lines than the model estimated.

The first thing to notice is the thick red line. This is the line estimated from the initial values of b0 and b1. You can see that this doesn’t fit the data points well at all and because of this it is has the highest error (MSE). However, you can see the lines gradually moving toward the data points until a line of best fit (the thick blue line) is identified. In other words, upon each iteration the model has learned better values for b0 and b1 until it finds the values that minimize the cost function. The final values that the model learns for b0 and b1 are 3.96 and 3.51 respectively — so very close the parameters 4 and 3.5 that we set!

Voilla! Our machine! it has learned!!

We can also visualize the decrease in the SSE across iterations of the model. This takes a steep decline in the early iterations before converging and stabilizing.

We can now use the learned values of b0 and b1 stored in theta to predict values y for new values of X.

Summary

This post presents a very simple way of understanding machine learning. It goes without saying that there is a lot more to ML, but gaining an initial intuition for the fundamentals of what is going on “underneath the hood” can go a long way toward improving your understanding of more complex models.

Источник

Cost Function is No Rocket Science!

This article was published as a part of the Data Science Blogathon.

The 2 main questions that popped up in my mind while working on this article were “Why am I writing this article?” & “How is my article different from other articles?” Well, the cost function is an important concept to understand in the fields of data science but while pursuing my post-graduation, I realized that the resources available online are too general and didn’t address my needs completely.

I had to refer to many articles & see some videos on YouTube to get an intuition behind cost functions. As a result, I wanted to put together the “What,” “When,” “How,” and “Why” of Cost functions that can help to explain this topic more clearly. I hope that my article acts as a one-stop-shop for cost functions!

Dummies guide to the Cost function 🤷‍♀️

Loss function: Used when we refer to the error for a single training example.
Cost function: Used to refer to an average of the loss functions over an entire training dataset.

But, like, *why* use a cost function?

Why on earth do we need a cost function? Consider a scenario where we wish to classify data. Suppose we have the height & weight details of some cats & dogs. Let us use these 2 features to classify them correctly. If we plot these records, we get the following scatterplot:

Fig 1: Scatter plot for height & weight of various dogs & cats

Blue dots are cats & red dots are dogs. Following are some solutions to the above classification problem.

Fig: Probable solutions to our classification problem

Essentially all three classifiers have very high accuracy but the third solution is the best because it does not misclassify any point. The reason why it classifies all the points perfectly is that the line is almost exactly in between the two groups, and not closer to any one of the groups. This is where the concept of cost function comes in. Cost function helps us reach the optimal solution. The cost function is the technique of evaluating “the performance of our algorithm/model”.

It takes both predicted outputs by the model and actual outputs and calculates how much wrong the model was in its prediction. It outputs a higher number if our predictions differ a lot from the actual values. As we tune our model to improve the predictions, the cost function acts as an indicator of how the model has improved. This is essentially an optimization problem. The optimization strategies always aim at “minimizing the cost function”.

Types of the cost function

There are many cost functions in machine learning and each has its use cases depending on whether it is a regression problem or classification problem.

1. Regression cost Function:

Regression models deal with predicting a continuous value for example salary of an employee, price of a car, loan prediction, etc. A cost function used in the regression problem is called “Regression Cost Function”. They are calculated on the distance-based error as follows:

Y’ – Predicted output

The most used Regression cost functions are below,

1.1 Mean Error (ME)

1.2 Mean Squared Error (MSE)

MSE = (sum of squared errors)/n

1.3 Mean Absolute Error (MAE)

So in this cost function, MAE is measured as the average of the sum of absolute differences between predictions and actual observations.

MAE = (sum of absolute errors)/n

It is robust to outliers thus it will give better results even when our dataset has noise or outliers.

2. Cost functions for Classification problems

Cost functions used in classification problems are different than what we use in the regression problem. A commonly used loss function for classification is the cross-entropy loss. Let us understand cross-entropy with a small example. Consider that we have a classification problem of 3 classes as follows.

Class(Orange,Apple,Tomato)

The machine learning model will give a probability distribution of these 3 classes as output for a given input data. The class with the highest probability is considered as a winner class for prediction.

The actual probability distribution for each class is shown below.

If during the training phase, the input class is Tomato, the predicted probability distribution should tend towards the actual probability distribution of Tomato. If the predicted probability distribution is not closer to the actual one, the model has to adjust its weight. This is where cross-entropy becomes a tool to calculate how much far the predicted probability distribution from the actual one is. In other words, Cross-entropy can be considered as a way to measure the distance between two probability distributions. The following image illustrates the intuition behind cross-entropy:

FIg 3: Intuition behind croos-entropy (credit – machinelearningknowledge.ai )

This was just an intuition behind cross-entropy. It has its origin in information theory. Now with this understanding of cross-entropy, let us now see the classification cost functions.

2.1 Multi-class Classification cost Functions

This cost function is used in the classification problems where there are multiple classes and input data belongs to only one class. Let us now understand how cross-entropy is calculated. Let us assume that the model gives the probability distribution as below for ‘n’ classes & for a particular input data D.

And the actual or target probability distribution of the data D is

Then cross-entropy for that particular data D is calculated as

Cross-entropy loss(y,p) = – y T log(p)

Cross-Entropy(y,P) = – (0*Log(0.1) + 0*Log(0.3)+1*Log(0.6)) = 0.51

The above formula just measures the cross-entropy for a single observation or input data. The error in classification for the complete model is given by categorical cross-entropy which is nothing but the mean of cross-entropy for all N training data.

Categorical Cross-Entropy = (Sum of Cross-Entropy for N data)/N

2.2 Binary Cross Entropy Cost Function

Binary cross-entropy is a special case of categorical cross-entropy when there is only one output that just assumes a binary value of 0 or 1 to denote negative and positive class respectively. For example-classification between cat & dog.

Let us assume that actual output is denoted by a single variable y, then cross-entropy for a particular data D is can be simplified as follows –

Cross-entropy(D) = – y*log(p) when y = 1

Cross-entropy(D) = – (1-y)*log(1-p) when y = 0

The error in binary classification for the complete model is given by binary cross-entropy which is nothing but the mean of cross-entropy for all N training data.

Binary Cross-Entropy = (Sum of Cross-Entropy for N data)/N

Conclusion

I hope you found this article helpful! Let me know what you think, especially if there are suggestions for improvement. You can connect with me on LinkedIn: https://www.linkedin.com/in/saily-shah/ and here’s my GitHub profile: https://github.com/sailyshah

The media shown in this article are not owned by Analytics Vidhya and is used at the Author’s discretion.

Источник