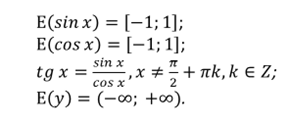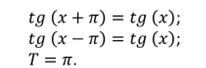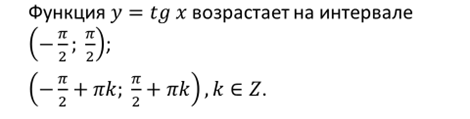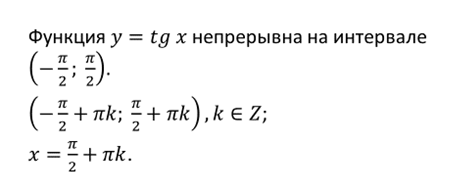Как начертить функцию y tgx

Презентация на тему «Функция y=tgx, её свойства и график»

Описание презентации по отдельным слайдам:

Функция y = tg x её свойства и график Автор: Брызгалова Наталья Юрьевна Преподаватель Архангельского техникума строительства и экономики

Цель: Изучить функцию y = tg x Задачи: 1. Изучить свойства функции у = tg x. 2. Уметь применять свойства функции у = tg x и читать график. 3. Формировать практические навыки построения графика функции у = tg x на основе изученного теоретического материала. 4. Закрепить понятия с помощью выполнения заданий.

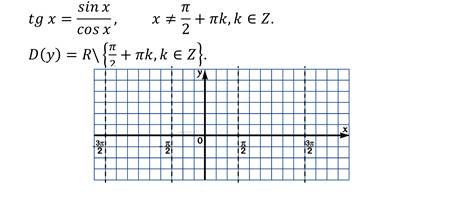
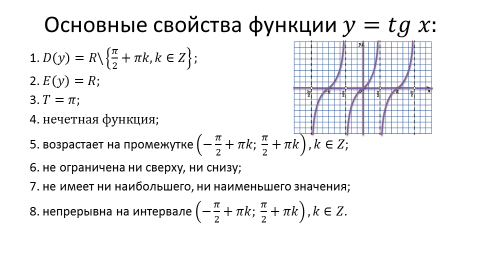
Функция y=tgx определена при x ≠ π/2+πn, n∈Z, является нечётной и периодической с периодом Т=π Поэтому достаточно построить её график на промежутке [0;π/2). Используя периодичность, строим график функции y=tg x на всей области определения. Затем, отобразив её симметрично относительно начала координат, получим график на интервале (−π/2;π/2).

Рассмотрим поведение функции и отметим важнейшие точки на промежутке [0;/2] Мы получили график функции на заданном промежутке.

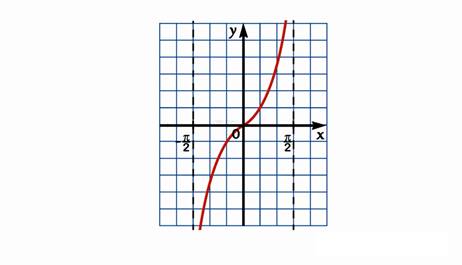
Ось тангенсов на тригонометрическом круге График y=tgx на промежутке (−π/2;π/2).

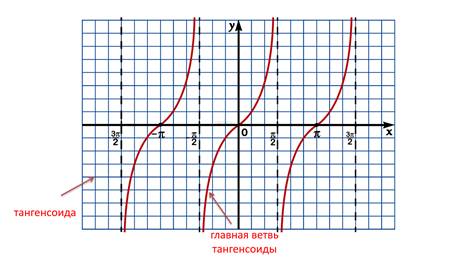
График функции y=tg x называют тангенсоидой. Главной ветвью графика функции y=tg x обычно называют ветвь, заключённую в полосе (−π/2;π/2). График функции y = tg x

8. Промежутки, на которых функция принимает положительные значения при x ∈ (πn; π/2+πn), n ∈ Z Промежутки, на которых функция принимает отрицательные значения при x ∈ (- π/2+πn; πn), n ∈ Z 9. Функция возрастает на x ∈ [−π/2 + πn; π/2+ πn], n ∈ Z

Решение задач Решить уравнение Задача №1 Решение На промежутке функция монотонно возрастает, значит, на этом промежутке значение достигается при единственном значении аргумента С учетом периодичности получаем

Задача №2 Найти все корни уравнения принадлежащие отрезку Решение Построим графики функций Графики пересекаются в трёх точках

Задача №3 Постройте график функций а) у = tg 2х; б) у = tgx; Решение а) б)

в) у = tg x + 2; г) у = tg (-x). Решение в) г)

Задача №4 Установить чётность или нечётность функции Решение Так как выполнено равенство y(-x) = у(х), то функция у(х) по определению четная.

Задания для самостоятельного решения 1) Постройте графики функций а) у = tg(x+ π/3); б) у = 3-tgx; в) у = tg (x + π/2) г) у = tg (x – π/3) д) у=tgx+5

2) Определить чётность или нечётность функции:

3) Решить графически уравнения:

4) Используя свойства функции у = tg x, сравните числа: 5) Используя свойства функции у = tg x, сравните числа:

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-1112703

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Хабаровске родители смогут заходить в школы и детсады только по QR-коду

Время чтения: 1 минута

В Липецкой области начинающие педагоги получат 120 тысяч рублей

Время чтения: 0 минут

В Минпросвещения рассказали о формате обучения школьников после праздников

Время чтения: 1 минута

В России утвердили новый порядок формирования федерального перечня учебников

Время чтения: 1 минута

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Петербургский Политех перевел студентов на дистанционку

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Урок «Функции y = tgx, y = ctgx, их свойства и графики»

Краткое описание документа:

В этом видеуроке рассмотрены свойства функций у = tgx, y = ctgx, показано, как построить их графики.

Видеоурок начинается с рассмотрения функции у = tgx.

Выделены свойства функции.

2) Функция у = tgxявляется периодической, где основной период равенπ. Это подтверждает равенство tg (x – π)=tg x = tg (x + π).Эти равенства изучались ранее, автор предлагает ученикам вспомнить их, указывая, что для любого допустимого значения tсправедливы равенства:

Далее перейдем к построению графика функции у = tgx. Как следует из свойств функции, описанных выше, функция у = tgx периодическая и нечетная. Поэтому достаточно построить часть графика – одну ветвь в одном промежутке, а затем воспользоваться симметрией для переноса. Автор приводит таблицу, в которой рассчитываются значения tgx при определенных значениях xдля более точного построения графика. Данные точки отмечаются на оси координат и соединяются плавной линией. Т.к. график симметричен относительно начала координат, то строится такая же ветвь, симметричная началу координат. В результате получаем одну ветвь графика у = tgx. Далее с помощью сдвига по оси х наπ, 2 πи так далее получается график у = tgx.

График функции у = tgx называется тангенсоида, а три ветви графика, показанные на рисунке – главные ветви тангенсоиды.

4) Функция у = tgx на каждом из промежутков (– + ; + ) возрастает.

5) График функции у = tgx не имеет ограничений сверху и снизу.

6) Функция у = tgx не имеет наибольшего и наименьшего значения.

7) Функция у = tgx непрерывна на любом промежутке (-–π/2+π;π/2+π). Прямая π/2+π называется асимптотой графика функции у = tgx, т.к. в этих точках график функции прерывается.

8) Множеством значений функции у = tgxназываются все действительные числа.

Далее в видеоуроке дается пример: решить уравнение с tgx. Для решения построим 2 графика функции у и найдем точки пересечения этих графиков: это бесконечное множество точек, абсциссы которых отличаются на πk. Корнем данного уравнения будет х = π/6 +πk.

Рассмотрим график функции у = ctgx. График функции можно построить двумя способами.

Первый способ предполагает построение графика аналогично построению графика функции у = tgx. Построим одну ветвь графика функции у = сtgxв промежутке между прямыми х = 0и х = π. Затем с помощью симметрии и периодичности построим другие ветви графика.

Второй способ более простой. График функции у = сtgxможно получить путем преобразования тангенсоиды с помощью формулы приведения сtgx = – tg (x + π/2). Для этого сдвинем одну ветвь графика функции у = tgxвдоль оси абсцисс на π/2вправо. Остальные ветви получаем путем сдвига этой ветви по оси х наπ, 2π и так далее. График функции у = ctgx называется также тангенсоида, а ветвь графика в промежутке (0;π) – главная ветвь тангенсоиды.

Мы рассмотрим свойства функции у = tg x ( игрек равно тангенс икс), у = ctg x( игрек равно котангенс икс), построим их графики. Рассмотрим функцию y = tgx

Прежде, чем строить график функции у = tg x, запишем свойства этой функции.

СВОЙСТВО 1. Областью определения функции у = tg x являются все действительные числа, кроме чисел вида х = + πk (икс равен сумме пи на два и пи ка).

СВОЙСТВО 2. Функция у = tg x является периодической с основным периодом π. (Так как справедливо двойное равенство

tg( x– π) = tgx = tg (x+π) тангенс от икс минус пи равен тангенсу икс и равен тангенсу от икс плюс пи). Это равенство мы рассматривали при изучении тангенса и котангенса. Напомним его:

Для любого допустимого значения t справедливы равенства:

Построим график функции у = tg x

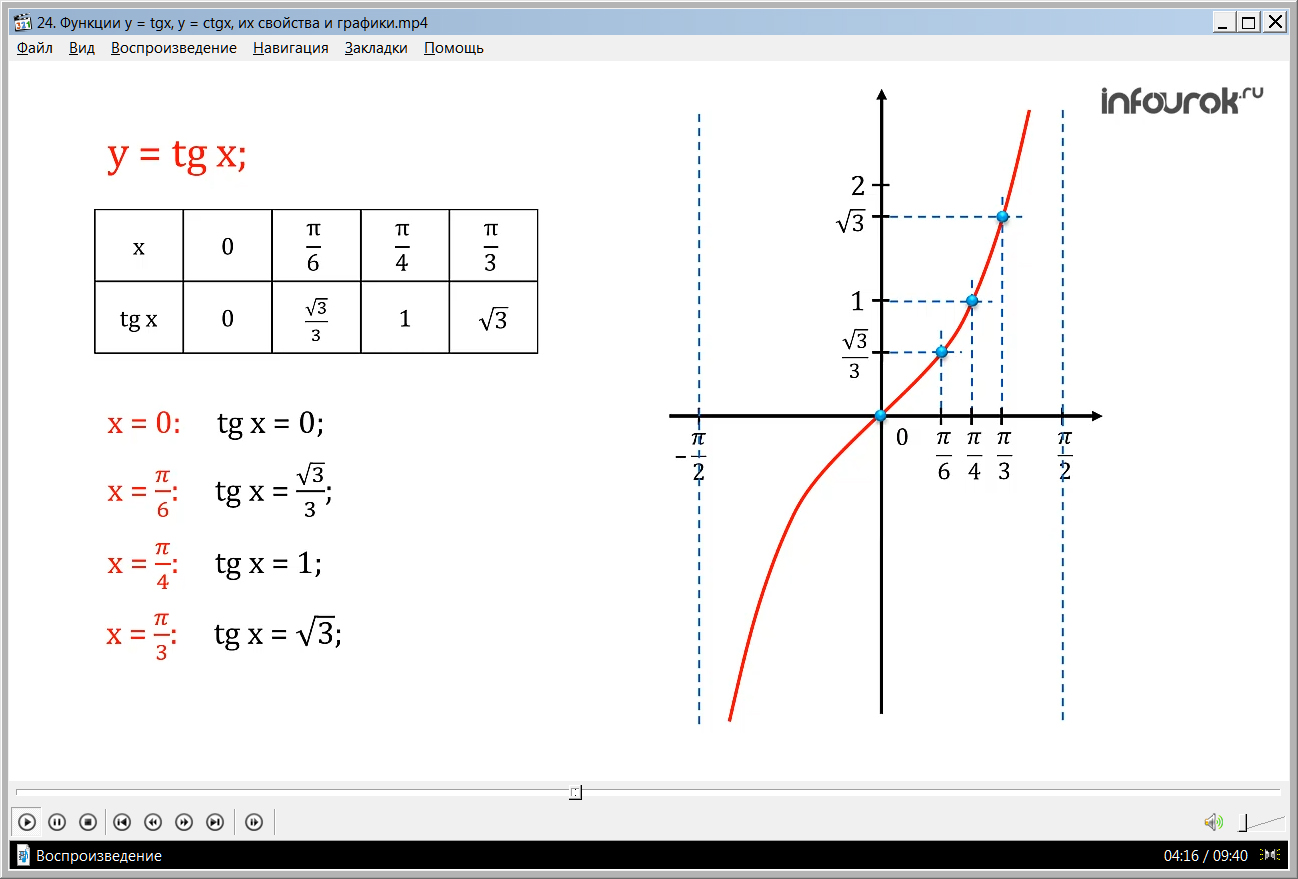
Построим таблицу значений тангенса для построения графика.

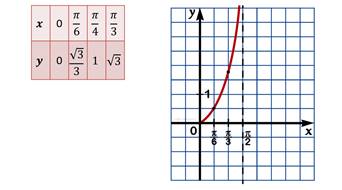
Находим первую точку: зная, что при х = 0 tg x = 0( икс равном нулю тангенс икс тоже равен нулю); следующая точка: при х = tg x = ( икс равном пи на шесть тангенс икс равен корень из трех на три); отметим следующие точки: при х = tg x = 1 (икс равном пи на четыре тангенс икс равен единице), а при х = tg x = ( икс равном пи на три тангенс икс равен корню квадратному из трех). Отметив полученные точки на координатной плоскости и соединим их плавной линией (рис. 2).

Так как график функции симметричен относительно начала координат, то построим такую же ветвь симметрично начала координат. (рис.3).

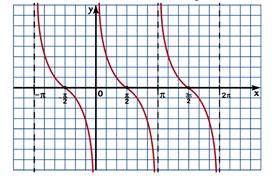
И, наконец, применив периодичность, получим график функции у = tg x.

Построенный график называется тангенсоида.

Изображенную на рисунке 3 часть тангенсоиды называют главной ветвью тангенсоиды.

На основании графика запишем еще свойства этой функции.

СВОЙСТВО 4. Функция у = tg x возрастает на каждом из промежутков (от минус пи на два плюс пи ка до пи на два плюс пи ка).

СВОЙСТВО 5. Функция у = tg x не ограничена ни сверху, ни снизу.

СВОЙСТВО 6. Функция у = tg x не имеет ни наибольшего, ни наименьшего значений.

СВОЙСТВО 7. Функция у = tg x непрерывна на любом интервале вида ( от минус пи на два плюс пи ка до пи на два плюс пи ка).

Прямая вида х = + πk (икс равно сумме пи на два и пи ка) является вертикальной асимптотой графика функции, так как в точках вида х = + πk функция терпит разрыв.

СВОЙСТВО 8. Множеством значений функции у = tg x являются все действительные числа, то есть ( е от эф равно промежутку от минус бесконечности до плюс бесконечности).

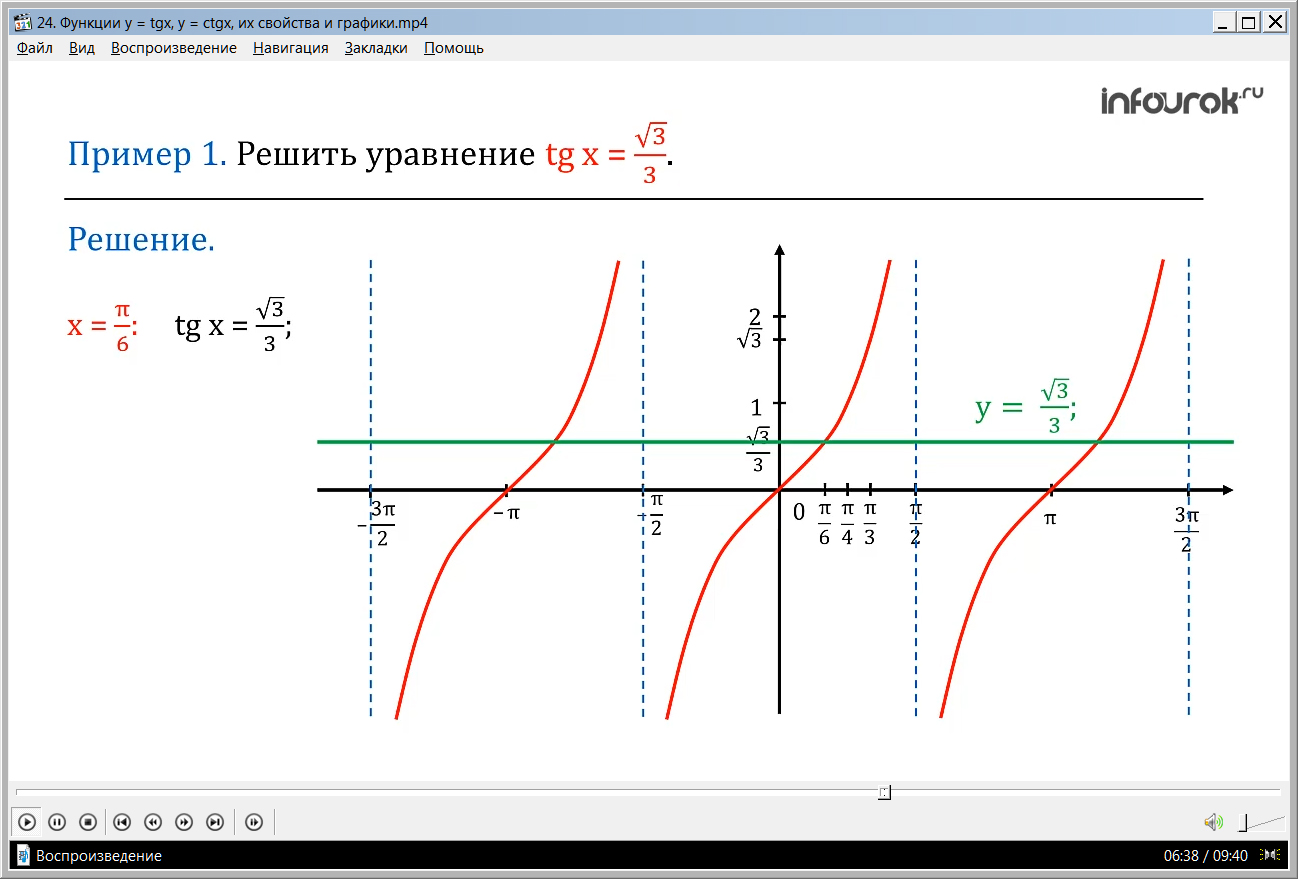
ПРИМЕР 1. Решить уравнение tg x = (тангенс икс равен корень из трех на три).

Решение. Построим в одной системе координат графики функций у = tg x

(игрек равен тангенсу икс) и у = ( игрек равен корню из трех, деленному на три).

Все решения данного уравнения запишем формулой х = + πk ( икс равно пи на шесть плюс пи ка).

Построим график функции у = сtg x.

Рассмотрим два способа построения.

Первый способ аналогичен построению графика функции у = tg x.

Воспользуемся таблицей значений котангенса для построения графика.

Отметив полученные точки на координатной плоскости и соединим их плавной линией.

Применим периодичность, получим график функции у = сtg x.

Мы построили ветвь графика функции у = сtg x в полосе от х = 0 и х =π. Строим остальные ветви путем сдвига построенной ветви по оси x на π, – π, 2π, – 2π и так далее.

Второй способ построения графика функции у =сtg x.

Получить график функции у =сtg x проще всего с помощью преобразования тангенсоиды, используя формулу приведения ( котангенс икс равно минус тангенс от суммы икс и пи на два).

При этом сначала, сдвинем ветвь графика функции у =tg x вдоль оси абсцисс на вправо, получим

у = tg (x+ ), а затем выполняем симметрию полученного графика относительно оси абсцисс. В результате получится ветвь графика функции у =сtg x (рис.4). Зная одну ветвь, можем построить весь график используя периодичность функции. Строим остальные ветви путем сдвига построенной ветви по оси x на π, 2π, и так далее.

График функции у =сtg x называется тоже тангенсоида, как и график функции у =tg x. Ветвь, которая заключена в промежутке от нуля до пи, называют главной ветвью графика функции у =сtg x.

Источник

Функции y=tgx, ctg x. Их свойства и графики

Урок 18. Алгебра 10 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Функции y=tgx, ctg x. Их свойства и графики»

· рассмотреть тангенс и котангенс как функции аргумента x;

· познакомиться с основным свойствам функций y=tg x, ctg x;

· построить графики функций y=tg x, ctg x.

Для того, чтобы найти область определения функции y = tg x давайте ещё раз вспомним определение тангенса x.

Найдём область значений функции y = tg x.

Найдём период функции y = tg x. И исследуем её на чётность.

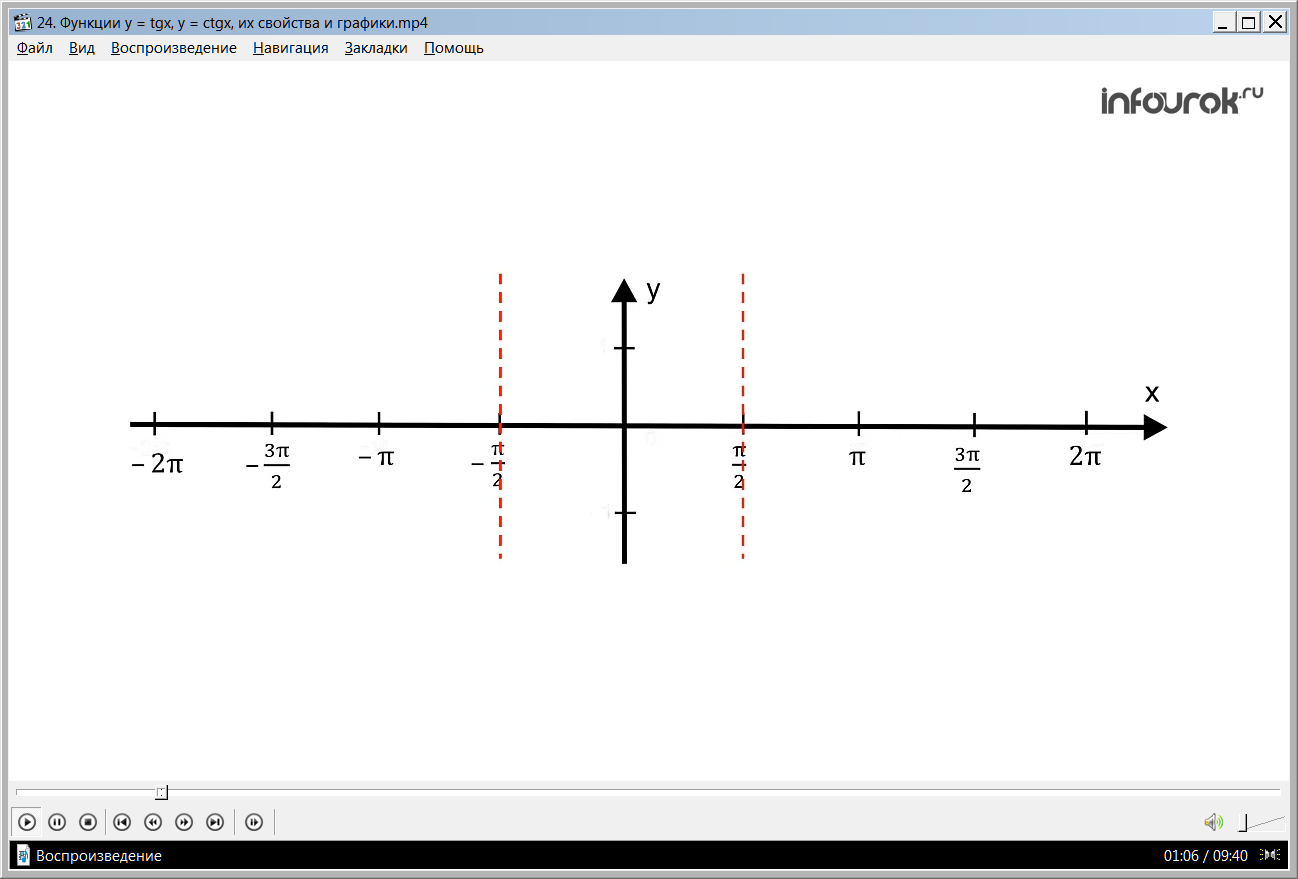
Поскольку функция y = tg x – периодичная функция с периодом π, то можно построить график функции на промежутке [-π/2; π/2], а затем сдвинуть построенную ветвь влево и вправо на π, 2π, 3π и так далее.

Поскольку функция нечётная, то можно построить на промежутке [0; π/2] и отобразить относительно начала координат.

Для построения графика на промежутке [0; π/2], составим таблицу значений тангенса для основных точек из этого промежутка. Отметим эти точки на координатной плоскости.

Отобразим полученную часть графика относительно начала координат.

Сдвинем построенную ветвь влево и вправо на π.

По построенному графику легко определить основные свойства функции y = tg x.

Исследование на монотонность.

Исследование на ограниченность.

Наибольшее и наименьшее значение функции.

Исследование на непрерывность.

Давайте, ещё раз перечислим все свойства функции y = tg x.

Проведя аналогичные рассуждения, можно построить график функции y = ctg x на промежутке [0; π], затем отразить симметрично относительно начала координат и сдвинуть получившуюся ветвь влево и вправо.

Давайте, перечислим все свойства функции y = ctg x.

Источник

Функция y = ctg x, её свойства и график

п.1. Развертка котангенса движения точки по числовой окружности в функцию от угла

При движении точки по числовой окружности на горизонтальной касательной, проведенной через точку (0;1), отображаются значения котангенсов соответствующих углов (см. §3 данного справочника).

Рассмотрим, как изменяется котангенс, если точка описывает полный круг, и угол x изменяется в пределах: 0≤x≤2π и построим график y=ctgx на этом отрезке.

Если мы продолжим движение по окружности для углов x > 2π, кривые продолжатся вправо; если будем обходить числовую окружность в отрицательном направлении (по часовой стрелке) для углов x главной ветвью графика котангенса.

п.2. Свойства функции y=ctgx⁡

2. Функция не ограничена сверху и снизу. Область значений \(y\in\mathbb\)

6. Функция убывает на всей области определения.

п.3. Примеры

Пример 2. Решите уравнение:
a) \(ctgx=-\sqrt<3>\)
Бесконечное множество решений: \(x=\frac<5\pi><6>+\pi k,\ k\in\mathbb\)

б) \(ctg\left(x+\frac\pi2\right)=0\)
\(x+\frac\pi2=\frac\pi2+\pi k\)
Бесконечное множество решений: \(x=\pi k,\ k\in\mathbb\)

в) \(ctg(2x)=1\)
\(2x=\frac\pi4+\pi k\)
Бесконечное множество решений: \(x=\frac<\pi><8>+\frac<\pi k><2>,\ k\in\mathbb\)

Пример 3. Постройте графики функций: a) \(y(x)=x^2-2tgx\cdot ctgx\)

Произведение \(tgx\cdot ctgx=1\). При этом ограничивается область определения функции \(y(x)\), т.к. \(tgx\) и \(ctgx\) имеют разрывы. Точки разрыва отмечены на числовой окружности: \(x\ne\frac<\pi k><2>\).

Сумма \(sin^2(tgx)+cos^2(tgx)=1\). При этом ограничивается область определения функции \(y(x)\), т.к. \(tgx\) имеeт разрывы. Точки разрыва отмечены на числовой окружности: \(x\ne\frac<\pi><2>+\pi k\).

Источник

Функция y = ctg x, её свойства и график

п.1. Развертка котангенса движения точки по числовой окружности в функцию от угла

При движении точки по числовой окружности на горизонтальной касательной, проведенной через точку (0;1), отображаются значения котангенсов соответствующих углов (см. §3 данного справочника).

Рассмотрим, как изменяется котангенс, если точка описывает полный круг, и угол x изменяется в пределах: 0≤x≤2π и построим график y=ctgx на этом отрезке.

Если мы продолжим движение по окружности для углов x > 2π, кривые продолжатся вправо; если будем обходить числовую окружность в отрицательном направлении (по часовой стрелке) для углов x главной ветвью графика котангенса.

п.2. Свойства функции y=ctgx⁡

2. Функция не ограничена сверху и снизу. Область значений \(y\in\mathbb\)

6. Функция убывает на всей области определения.

п.3. Примеры

Пример 2. Решите уравнение:
a) \(ctgx=-\sqrt<3>\)
Бесконечное множество решений: \(x=\frac<5\pi><6>+\pi k,\ k\in\mathbb\)

б) \(ctg\left(x+\frac\pi2\right)=0\)
\(x+\frac\pi2=\frac\pi2+\pi k\)
Бесконечное множество решений: \(x=\pi k,\ k\in\mathbb\)

в) \(ctg(2x)=1\)
\(2x=\frac\pi4+\pi k\)
Бесконечное множество решений: \(x=\frac<\pi><8>+\frac<\pi k><2>,\ k\in\mathbb\)

Пример 3. Постройте графики функций: a) \(y(x)=x^2-2tgx\cdot ctgx\)

Произведение \(tgx\cdot ctgx=1\). При этом ограничивается область определения функции \(y(x)\), т.к. \(tgx\) и \(ctgx\) имеют разрывы. Точки разрыва отмечены на числовой окружности: \(x\ne\frac<\pi k><2>\).

Сумма \(sin^2(tgx)+cos^2(tgx)=1\). При этом ограничивается область определения функции \(y(x)\), т.к. \(tgx\) имеeт разрывы. Точки разрыва отмечены на числовой окружности: \(x\ne\frac<\pi><2>+\pi k\).

Источник