Как начертить гиперболу инженерная графика
Отдельные участки овалов являются кривыми постоянной кривизны они могут быть начерчены с помощью циркуля, в связи с чем их называют циркульными кривыми. Кривые, имеющие переменную кривизну, вычерчивают с помощью лекал и называют лекальными кривыми. К лекальным кривым относятся: эллипс, парабола, гипербола, эвольвента окружности, различного вида циклоиды, синусоиды, различные спирали. Многие лекальные кривые образуются в результате плоски сечений различных поверхностей. Так, например, эллипс, парабола и гипербола образуются при пересечении поверхности конуса плоскостями различного наклона.
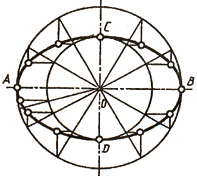
Эллипс. Геометрическое место точек плоскости, сумма расстояний от которых до двух заданных точек, называемых фокусами, есть величина постоянная, называется эллипсом. Существует много способов вычерчивания эллипса. Наиболее распространенным является способ двух окружностей, диаметры которых равны большой и малой осям эллипса. Если через центр О провести произвольный диаметр, то он пересечет окружности в точках Е, F и G, Н. Через полученные точки проводят-прямые, параллельные осям эллипса; пересечение этих прямых определит две точки эллипса К и L. Обычно диаметры проводят, деля одну из окружностей на 12 равных частей.
Пусть требуется вписать эллипс в параллелограмм. Принимают нижнюю сторону параллелограмма за сторону квадрата, строят на ней квадрат и вписывают в него окружность. Центру О окружности будет соответствовать центр О’ эллипса, диаметру АВ окружности будет соответствовать сопряженный диаметр А’В’ эллипса и т. д. Делят половину диаметра OD и половину сопряженного диаметра O’D’ на равные части (например, на четыре) и проводят через точки деления линии, параллельные АВ. На соответственных прямых будут находиться соответствующие точки окружности и эллипса, например Е и Е’. Получают эти точки с помощью ломаных прямых, параллельных ломаной ODO’. В технике эллипсы встречаются в спицах маховиков, в эллиптических зубчатых колесах.
Глава 3. Некоторые геометрические построения
§ 22. Лекальные кривые
Лекальными называют плоские кривые, вычерченные с помощью лекал по предварительно построенным точкам. К лекальным кривым относят: эллипс, параболу, гиперболу, циклоиду, синусоиду, эвольвенту и др.
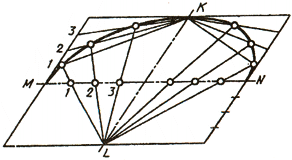
Можно привести пример построения эллипса по двум сопряженным диаметрам (рис. 37, б) MN и KL. Сопряженными два диаметра называют, если каждый из них делит пополам хорды, параллельные другому диаметру. На сопряженных диаметрах строят параллелограмм. Один из диаметров MN делят на равные Части; на такие же части делят и стороны параллелограмма, параллельные другому диаметру, нумеруя их, как показано на чертеже. Из концов второго сопряженного диаметра KL через точки деления проводят лучи, в пересечении которых получают точки эллипса.
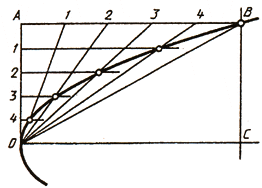
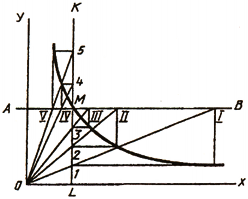
Рассмотрим пример построения параболы по ее вершине О и какой-либо точке В (рис. 38, а). С этой целью строят прямоугольник ОАВС и делят его стороны на равные части, из точек деления проводят лучи. В пересечении одноименных лучей получают точки параболы.
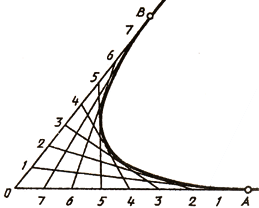
Можно привести пример построения параболы в виде кривой, касательной прямым с заданными на них точками А и В (рис. 38, б). Стороны угла, образованного этими прямыми, делят на равные части и нумеруют точки деления. Одноименные точки соединяют прямыми. Параболу вычерчивают как огибающую зтак прямых.
Гиперболой называют плоскую незамкнутую кривую второго порядка, состоящую из двух веток, концы которых удаляются в бесконечность, стремясь к своим ассимптотам. Гипербола отличается тем, что каждая точка ее обладает особым свойством: разность ее расстояний от двух данных точек-фокусов есть величина постоянная, равная расстоянию между вершинами кривой. Если ассимптоты гиперболы взаимно перпендикулярны, она называется равнобокой. Равнобокая гипербола широко применяется для построения различных диаграмм, когда задана своими координатами одна точка М (рис. 38, в). В этом случае через заданную точку проводят линии АВ и KL параллельно координатным осям. Из полученных точек пересечения проводят линии, параллельные координатным осям. В их пересечении получают точки гиперболы.
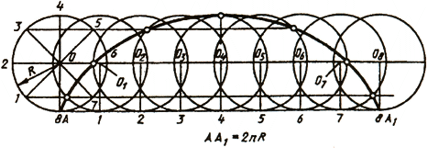
Циклоидой называют кривую линию, представляющую собой траекторию точки А при перекатывании окружности (рис. 39). Для построения циклоиды от исходного положения точки А откладывают отрезок АА1 отмечают промежуточное положение точки А. Так, в пересечении прямой, проходящей через точку l, окружностью, описанной из центра О1, получают первую точку циклоиды. Соединяя плавной прямой построенные точки, Получают циклоиду.
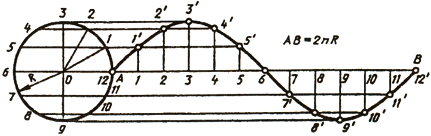
Синусоидой называют плоскую кривую, изображающую изменение синуса в зависимости от изменения его угла. Для построения синусоиды (рис. 40) нужно разделить окружность на равные части и на такое же количество равных частей разделить отрезок прямой АВ = 2nR. Из одноименных точек деления провести взаимно перпендикулярные линии, в пересечении которых получают точки, принадлежащие синусоиде.


© Красноярский государственный аграрный университет
© Управление информационных технологий
© Кафедра Технологии машиностроения
Глава 3. Некоторые геометрические построения
§ 22. Лекальные кривые
Лекальными называют плоские кривые, вычерченные с помощью лекал по предварительно построенным точкам. К лекальным кривым относят: эллипс, параболу, гиперболу, циклоиду, синусоиду, эвольвенту и др.
Можно привести пример построения эллипса по двум сопряженным диаметрам (рис. 37, б) MN и KL. Сопряженными два диаметра называют, если каждый из них делит пополам хорды, параллельные другому диаметру. На сопряженных диаметрах строят параллелограмм. Один из диаметров MN делят на равные Части; на такие же части делят и стороны параллелограмма, параллельные другому диаметру, нумеруя их, как показано на чертеже. Из концов второго сопряженного диаметра KL через точки деления проводят лучи, в пересечении которых получают точки эллипса.
Рассмотрим пример построения параболы по ее вершине О и какой-либо точке В (рис. 38, а). С этой целью строят прямоугольник ОАВС и делят его стороны на равные части, из точек деления проводят лучи. В пересечении одноименных лучей получают точки параболы.
Можно привести пример построения параболы в виде кривой, касательной прямым с заданными на них точками А и В (рис. 38, б). Стороны угла, образованного этими прямыми, делят на равные части и нумеруют точки деления. Одноименные точки соединяют прямыми. Параболу вычерчивают как огибающую зтак прямых.
Гиперболой называют плоскую незамкнутую кривую второго порядка, состоящую из двух веток, концы которых удаляются в бесконечность, стремясь к своим ассимптотам. Гипербола отличается тем, что каждая точка ее обладает особым свойством: разность ее расстояний от двух данных точек-фокусов есть величина постоянная, равная расстоянию между вершинами кривой. Если ассимптоты гиперболы взаимно перпендикулярны, она называется равнобокой. Равнобокая гипербола широко применяется для построения различных диаграмм, когда задана своими координатами одна точка М (рис. 38, в). В этом случае через заданную точку проводят линии АВ и KL параллельно координатным осям. Из полученных точек пересечения проводят линии, параллельные координатным осям. В их пересечении получают точки гиперболы.
Циклоидой называют кривую линию, представляющую собой траекторию точки А при перекатывании окружности (рис. 39). Для построения циклоиды от исходного положения точки А откладывают отрезок АА1 отмечают промежуточное положение точки А. Так, в пересечении прямой, проходящей через точку l, окружностью, описанной из центра О1, получают первую точку циклоиды. Соединяя плавной прямой построенные точки, Получают циклоиду.
Синусоидой называют плоскую кривую, изображающую изменение синуса в зависимости от изменения его угла. Для построения синусоиды (рис. 40) нужно разделить окружность на равные части и на такое же количество равных частей разделить отрезок прямой АВ = 2nR. Из одноименных точек деления провести взаимно перпендикулярные линии, в пересечении которых получают точки, принадлежащие синусоиде.


© Красноярский государственный аграрный университет
© Управление информационных технологий
© Кафедра Технологии машиностроения
Построение лекальных кривых
Коробовые кривые и овалы состоят из нескольких дуг различного радиуса. Это значит, что на всем протяжении каждой дуги кривизна кривой остается постоянной. Но есть много кривых, кривизна которых изменяется непрерывно на каждом элементе кривой, для их выполнения существуют так называемые лекала, поэтому и кривые называются лекальными кривыми. Для построения такой кривой сначала находят несколько точек (не менее трех), по которым проводят плавную линию.
К лекальным кривым, вычерчиваемым по точкам, относятся кривые различных диаграмм и так называемые плоские кривые второго порядка:
Эллипсом называется замкнутая кривая, сумма расстояний каждой точки которой от двух данных точек, называемых фокусами, постоянна (Рисунок 1) 1F1+1F2=2F1+2F2=. nF1+nF2=const.
Рассмотрим пример построения эллипса по заданному расстоянию между фокусами F1 и F и его большой оси АВ (Рисунок 2). Для этого откладываем от точек А и В по половине расстояния между фокусами и получаем точки Е и Е1 (таким же образом можно использовать любую точку, взятую на АВ между фокусами). Через точку О перпендикулярно АВ проводим линию, на которой будет расположена малая ось эллипса СD. Для этого делаем засечки на этой прямой из точки F1 или F радиусом, равным половине длины большой оси, и получаем малую ось эллипса CD.
Чтобы получить одну точку, принадлежащую эллипсу, необходимо из фокуса F2 провести дугу R=AE, а из фокуса F1 провести дугу R=BE, в пересечении дуг получим точку I, принадлежащую эллипсу, так как AE+BE=AB. Таким же способом определяют любую точку эллипса, например точку II, для чего на АВ надо взять точку К.
Параболой называется плоская кривая, каждая точка которой расположена на одинаковом расстоянии от заданной прямой, называемой директрисой, и от точки, называемой фокусом параболы (Рисунок 4): BK=KF, B1K1=K1F и т.д. Расстояние между фокусом и директрисой называется параметром параболы, от которого и зависит очертание этой кривой. С изменением параметра изменяется и парабола: чем меньше параметр, тем она уже, чем больше, тем парабола шире.











 Построение лекальных кривых осуществляют следующим образом:
Построение лекальных кривых осуществляют следующим образом: