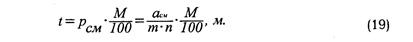Как начертить линейку поперечного масштаба

Поперечный масштаб

Поперечный масштаб, в отличие от линейного масштаба, позволяет измерять и переносить линии на карту или план с большей точностью.

Обычно поперечный масштаб наносят на металлическую пластину, но его также можно построить на бумаге.

Начало построения поперечного масштаба аналогично построению линейного масштаба.

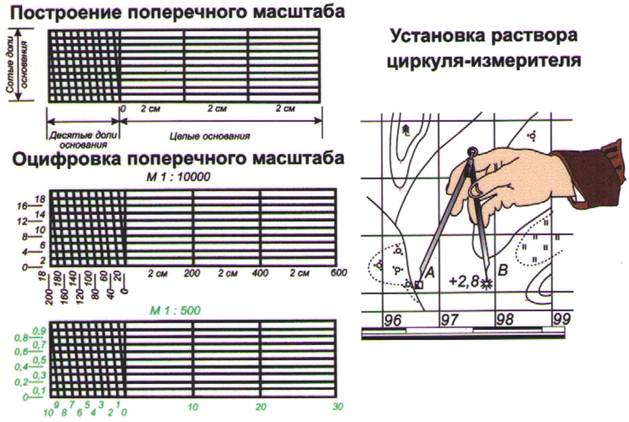
Далее с конца каждого основания линейного масштаба ставят перпендикуляры одинаковой длины (обычно длину перпендикуляров принимают равной 2 см).

Два крайних перпендикуляра делят на 10 равных частей и через полученные точки проводят линии, параллельные основанию масштаба.

Верхнее левое основание, также как и нижнее левое основание, делят на 10 равных частей.

Точки деления левого верхнего основания и нижнего левого основания соединяют наклонными линиями как показано на рисунке. Эти наклонные линии называют трансверсалями.

Возле трансверсалей подписывают деления, которые равны сотой доле основания масштаба (100 м / 100 = 1 м).

На рисунке изображен поперечный масштаб с основанием 2 см соответствующие численному масштабу 1:5000 (2 см * 5000 = 10000 см = 100 м).

Таким образом, поперечный масштаб позволяет измерять и откладывать линии на карте или плане с точностью до сотой доли основания масштаба (1 м для численного масштаба 1:5000).

Поперечный масштаб используют следующим образом:

1). в раствор циркуля-измерителя с карты или плана берут отрезок, длину которого необходимо определить;

2). прикладывают циркуль к поперечному масштабу таким образом, чтобы его правая иголка находилась на нулевом или другом находящимся справа от нуля перпендикуляре, а левая иголка была на одной горизонтальной линии с правой иголкой;

3). суммируют отсчеты по перпендикулярам на правой и левой иголках циркуля справа и слева от нулевого перпендикуляра.

На рисунке длины измеренных отрезков по плану масштаба 1:5000 равны 252 метра и 477 метров.

Источник

Поперечный масштаб

Размеры участков земной поверхности и предметов, на них расположенных, так велики, что они не могут быть изображены на бумаге без соответствующего уменьшения. Чтобы изображение местности на плане было подобно самой местности, все горизонтальные проекции линий местности изображают на плане уменьшенными в одинаковое число раз. Степень такого уменьшения называется масштабом плана.

Для повышения точности применяют поперечный масштаб, который представляет график, построенный на основании линейного масштаба.

Поперечный масштаб применяют для измерений и построений повышенной точности. Обычно поперечный масштаб гравируют на металлических пластинах, линейках, или на транспортирах, а также он может быть построен на чертеже для заданного числового масштаба.

Поперечный масштаб строят следующим образом. На прямой линии откладывают несколько раз основание масштаба равное 2 см, называемое основанием масштаба. Первое основание делят на 10 равных частей и на правом конце его пишут нуль, а на левом – то число метров или километров, которому на местности соответствует в данном масштабе основание. Вправо от нуля над каждым делением надписывают значения соответствующих расстояний на местности (рис. 19). Из каждой точки подписанного деления восставляют перпендикуляры, на которых откладывают десять отрезков, равных десятой доли основания.

Через точки, полученные на перпендикулярах, проводят прямые линии, параллельные основанию. Верхнюю линию над первым основанием делят также на десять равных частей. Полученные точки верхних и нижних делений на первом отрезке соединяют, как показано на рисунке 19. Полученные линии называются трансверсалями. Расстояние между смежными трансверсалями составляют десятую долю основания, а между нулевой вертикальной линией и смежной с ней трансверсалью – от одной сотой доли до десятой.

Рис. 19. Поперечный масштаб

Длину линии на плане берут в раствор циркуля и переносят его на нижнюю линию масштаба. Если иглы ножек циркуля точно совпадают с делениями масштаба, делают отсчет расстояния.

Если ножки циркуля не точно совпадают с делением масштаба, его перемещают вверх от одной параллели к другой, пока игла левой ножки будет точно лежать на наклонной прямой, а игла правой ножки – на вертикали справа от нуля или на нуле.

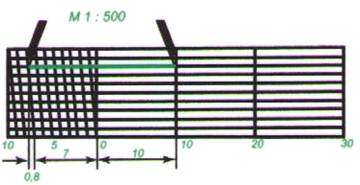
Длина отрезка на плане в мерах длины на местности (рис. 20) в масштабе 1: 500 составляет 17,8 м.

Рис. 20. Определение длин линий при помощи поперечного масштаба

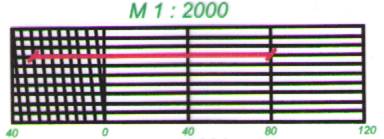
Требуется на план масштаба 1: 2000 наложить линию местности, равную 110,8 м (см. рис. 21). Рассуждаем так. Вправо от нуля до второй вертикали имеем 80 м, семь делений слева от нуля дают (7*4) 28 м; 2,8 м получим, поднимаясь вверх по наклонной прямой до седьмой горизонтали (7*0,4). Поставим на этой горизонтали иглы ножек циркуля, получим в растворе циркуля отрезок на плане, равный 110,8 м на местности. Не меняя раствора циркуля, этот отрезок и накладываем на план.

Рис. 21. Определение длин линий при помощи поперечного масштаба

При помощи поперечного масштаба можно взять отрезок с точностью 0,1 мм. Отрезок в 0,1 мм воспринимается невооруженным глазом в виде точки.

Длина линии местности, соответствующая 0,1 мм на плане, называется точностью масштаба и обозначается t_m. Она зависит от численного масштаба.

Точность масштаба имеет большое практическое значение.

По точности масштаба устанавливают, при изображении каких объектов на плане можно сохранить подобие, какие объекты в данном масштабе не изображаются.

Точность масштаба 1: 25000 равна 2,5 м.

Расчет можно вести следующим образом:

В 0,1 мм – 2,5 м или tm = 0,1 мм · 25000 = 2,5 м.

Источник

Как построить поперечный масштаб, если известны его основание и численный масштаб.

Поперечный масштаб, в отличие от линейного масштаба, позволяет измерять и переносить линии на карту или план с большей точностью.

Обычно поперечный масштаб наносят на металлическую пластину, но его также можно построить на бумаге.

Начало построения поперечного масштаба аналогично построению линейного масштаба.

Далее с конца каждого основания линейного масштаба ставят перпендикуляры одинаковой длины (обычно длину перпендикуляров принимают равной 2 см).

Два крайних перпендикуляра делят на 10 равных частей и через полученные точки проводят линии, параллельные основанию масштаба.

Верхнее левое основание, также как и нижнее левое основание, делят на 10 равных частей.

Точки деления левого верхнего основания и нижнего левого основания соединяют наклонными линиями как показано на рисунке. Эти наклонные линии называют трансверсалями.

Возле трансверсалей подписывают деления, которые равны сотой доле основания масштаба (100 м / 100 = 1 м).

На рисунке изображен поперечный масштаб с основанием 2 см соответствующие численному масштабу 1:5000 (2 см * 5000 = 10000 см = 100 м).

Таким образом, поперечный масштаб позволяет измерять и откладывать линии на карте или плане с точностью до сотой доли основания масштаба (1 м для численного масштаба 1:5000

11. Дайте определения и понятия плана, карты, профиля.

Топографическим планомназывают уменьшенное и подобное изображение на плоскости ( на листе бумаги ) в ортогональной проекции местных предметов и рельефа малых по размеру участков земной поверхности, принимаемых за плоскость ( размером 20х20 кв. км ). Иногда план составляют без изображения рельефа. В этом случае его называют ситуационным или контурным.

Участки земной поверхности изображаются на плане без учёта её кривизны, так как размеры этих участков малы.

Значительные по своим размерам участки земной поверхности невозможно получить непосредственно на плоскости без существенных искажений, т.е. с сохранением полного подобия. Такие участки проектируют ортогонально на поверхность земного эллипсоида, а с неё в какой-либо картографической проекции, переносят на плоскость. Полученное таким образом уменьшенное изображение земной поверхности на плоскости называется картой.

Таким образом, картой называют уменьшенное, подобное изображение земной поверхности на плоскости, построенное в какой-либо картографической проекции.

Участки земной поверхности изображаются на карте с учётом её кривизны вследствие больших размеров этих участков.

Карта, составленная в проекции Гаусса-Крюгера с изображением ситуации и рельефа называется топографической.

Кроме карт и планов к топографическим материалам относят профили.

Профили местности представляют собой уменьшенное изображение вертикального разреза земной поверхности вдоль выбранного или заданного направления. Они являются топографической основой при составлении проектно-технической документации, необходимой при строительстве подземных и наземных трубопроводов, дорог и других коммуникаций.

Источник

Решение задач по топографическим планам

Масштабы: численный, линейный и поперечный

Масштабом

горизонтальным проложением линии

Применяется три типа масштаба:

численный, линейный и поперечный.

Численным масштабом

Численный масштаб – величина неименованная. Он записывается так: 1:1000, 1:2000, 1: 5000 и т.д., причём в такой записи 1000, 2000 и 5000 называется знаменателем масштаба М.

Численный масштаб говорит о том, что в одной единице длины линии на плане (карте ) содержится точно столько же единиц длины на местности. Так, например, в одной единице длины линии на плане 1:5000 содержится точно 5000 таких же единиц длины на местности, а именно: один сантиметр длины линии на плане 1:5000 соответствует 5000 сантиметрам на местности (т.е. 50 метрам на местности); в одном миллиметре длины линии на плане 1:5000 содержится 5000 миллиметров на местности (т.е. в одном миллиметре длины линии на плане 1:5000 содержится 500 сантиметров или 5 метров на местности) и т.д.

При работе с планом в ряде случаев пользуются линейным масштабом.

Линейный масштаб

Рис.1

Основанием линейного масштаба называется отрезок АВ линейного масштаба (основная доля масштаба), равный обычно 2 см. Он переводится в соответствующую длину на местности и подписывается. Крайнее левое основание масштаба делят на 10 равных частей.

Наименьшее деление основания линейного масштаба равно 1/10 основания масштаба.

Пример: для линейного масштаба (использующегося при работе на топографическом плане масштаба 1:2000), показанного на рисунке 1, основание масштаба АВ равно 2 см (т.е. 40 метрам на местности), а наименьшее деление основания равно 2 мм, что в масштабе 1:2000 соответствует 4 м на местности.

Отрезок cd (рис. 1), взятый с топографического плана масштаба 1:2000, состоит из двух оснований масштаба и двух наименьших делений основания, что, в итоге, соответствует на местности 2х40м+2х2м = 88 м.

Поперечный масштаб

Основание AB нормального поперечного масштаба равно, как и в линейном масштабе, также 2 см. Наименьшее деление основания равно CD =1/10 АВ= 2мм. Наименьшее деление поперечного масштаба равно cd = 1/10 CD =1/100 АВ = 0,2мм (что следует из подобия треугольника BCD и треугольника Bcd).

Таким образом, для численного масштаба 1:2000 основание поперечного масштаба будет соответствовать 40 м, наименьшее деление основания (1/10 основания) равно 4 м, а наименьшее деление масштаба 1/100 АВ равно 0,4 м.

Остановимся на одной из важнейших характеристик понятия «масштаб».

Точностью масштаба называется горизонтальный отрезок на местности, который соответствует величине 0,1 мм на плане данного масштаба. Эта характеристика зависит от разрешающей способности невооруженного человеческого глаза, которая (разрешающая способность) позволяет рассмотреть минимальное расстояние на топографическом плане в 0.1мм. На местности эта величина будет уже равна 0.1 мм х М, где М – знаменатель масштаба.

Рис.2

Поперечный масштаб, в частности, позволяет измерить длину линии на плане (карте) масштаба 1:2000 именно с точностью данного масштаба.

Пример: в 1 мм плана 1:2000 содержится 2000 мм местности, а в 0,1мм, соответственно, 0,1 x М (мм) = 0.1 х 2000 мм = 200 мм = 20 см, т.е. 0,2 м.

Поэтому при измерении (построении) на плане длины линии ее значение следует округлить с точностью масштаба. Пример: при измерении (построении) линии длиной 58,37 м (рис. 3), ее значение в масштабе 1:2000 (с точностью масштаба 0,2 м) округляется до 58,4 м, а в масштабе 1:500 (точность масштаба 0,05 м) – длина линии округляется уже до 58,35 м.

Рис.3

Чтение
топографических планов

Для пользования топографическими планами необходимо изучить условные знаки, принятые для данного масштаба. Условные знаки – графические обозначения, которые показывают местоположение предметов и явлений, а также их количественные и качественные характеристики. Они издаются в виде отдельных таблиц или таблиц на учебных планах. Условные знаки делятся на масштабные (контурные), и внемасштабные.

Масштабными называются условные знаки, которыми местные предметы изображаются в масштабе данного плана, т.е. крупные объекты, например, пашни, луга, леса, моря, озера и т.п.

Внемасштабные условные знаки – знаки, показывающие предметы, которые вследствие своей малости не могут быть изображены в масштабе плана (ширина дорог, колодцы, родники, мосты, опоры ЛЭП, столбы электросети и т.д.). Величина этих знаков не соответствует истинным размерам изображаемых предметов.

Скачать условные знаки для топографических планов:

Задачи, решаемые
по топографическим планам

По топографическому плану можно решить ряд задач, в том числе определить: прямоугольные координаты точки; длину линии; дирекционный угол и румб линии; отметку точки; уклон, крутизну ската и др. Порядок решения этих задач показан на примере учебного плана масштаба 1:2000.

Определение прямоугольных
координат точек

Пример : запись 79,2 означает, что абсцисса линии сетки Х = 79,2 км, т.е. отстоит по оси Х от начала координат на 79200 м. Запись 66,2 означает, что ордината линии сетки Y = 66,2 км, т.е. отстоит по оси У от начала координат на 66200 м.

Для быстрого нахождения какой-нибудь точки на топографическом плане указывают нижний левый угол соответствующего квадрата сетки координат.

Сначала записывают в метрах абсциссу Х (южной) линии квадрата, в котором находится точка А, т.е. Х(южной линии сетки) =79200,0 м. Циркулем и поперечным масштабом определяют расстояние Δх = Y(а)-Y(А) также в метрах с точностью масштаба. Полученную величину Δх=64,8 м прибавляют к абсциссе нижней (южной) линии квадрата Х(южной линии сетки) =79200,0 м и находят абсциссу точки А: Х(А) = 79200,0 + 64,8 = 79264,8 м.

Рис.4

Аналогично определяют ординату точки А: к значению ординаты западной линии сетки квадрата У(западной линии сетки) =66200,0 м прибавляют длину отрезка Δy =y(A)-y(b), равную 141,6 м, и получают Y(А) = 66200,0 + 141,6 = 66341,6 м.

Измерение длин линий

Расстояние между точками А и В измеряется циркулем, значение длины линии АВ находится по поперечному масштабу и записывается с точностью масштаба.

Определение
дирекционного угла

Дирекционным углом α называется горизонтальный угол, отсчитываемый от северного направления осевого меридиана, по ходу часовой стрелки, до направления данной линии.

Дирекционный угол α линии АВ можно измерить с помощью транспортира. На рис. 5 представлены дирекционные углы α₁, α₂, α₃, и α₄ четырех линий М-1, М-2, М-3, М-4.

Рис.5

Рис.6

Связь между прямым и обратным дирекционными углами выглядит так:

Рис.7

Например, если прямой румб равен r _пр = СВ: 350º, то обратный румб равен r _обр= ЮЗ: 350º.

Рис.8

Таблица перехода от дирекционных углов α к румбам r приведена ниже.

Формулы перехода от дирекционных углов к румбам

Определение отметок точек
и крутизны ската линии местности

Высотой Н точки местности называется расстояние по направлению отвесной линии от точки до уровенной поверхности.

Отметкой точки местности называется численное значение высоты точки. Например, Н(А) = 150 м, Н(В) =149 м.

На топографическом плане рельеф изображается надписями отметок отдельных характерных точек, условными знаками (промоина, обрыв и т. п.) и горизонта-лями.

Горизонталями называются замкнутые кривые линии, со-единяющие точки местности с одинаковыми отметками. Горизонтали образуются путём пересечения поверхности местности секущими горизонтальными плоскостями, проведенными через заданное расстояние, которое называется высотой сечения рельефа h.

Заложением называется расстояние d на плане между двумя соседними горизонталями (рис. 9 – 11).

Рис.9

По отметкам двух смежных (соседних) горизонталей можно определить отметку точки, лежащей между ними. Например: отметка первой точки В на нижней (рис. 10) горизонтали H1 = 161 м, отметка второй точки А на верхней (рис. 10) горизонтали H2 = 162 м (т.е. высота сечения рельефа h = 1 м), заложение d = 16,8 м, расстояние от первой горизонтали до точки С равно с = 7,6 м (рис. 10). Тогда (с требуемой точностью до 0,1 м) вычисляем отметку НС точки С по формуле

Рис.11

Чем больше угол наклона, тем скат круче.

Для нашего примера уклон линии местности между горизонталями равен

Источник

Лекция № 5

ТОЧНОСТЬ КАРТ И ПЛАНОВ. МАСШТАБЫ

1. Понятие точности измерения и его отображения на карте и плане.

2. Понятие масштаба, виды масштабов.

3. Численный масштаб.

4. Линейный масштаб.

5. Поперечный масштаб

1. Предельная и графическая точности масштабов.При оценке точ­ности нанесения точек на план следует исходить из физиологических возможностей человеческого глаза. Как известно, глаз человека спосо­бен отчетливо различать две точки, если они располагаются под утлом не менее 60″ к наблюдателю. При меньшем угле зрения глаз восприни­мает две точки слившимися в одну. Расстоянию наилучшего зрения, равному 25 см, углу в 60 » соответствует отрезок, равный 0,1 мм. Таков, например, диаметр кружка от укола остро отточенной иглы. Отсюда следует, что на плане (карте) в самом благоприятном случае можно изобразить лишь такие горизонтальные проекции линий местности, которым в данном масштабе соответствует отрезок 0,1 мм и более.

Горизонтальное расстояние на местности, соответствующее в данном масштабе 0,1 мм (0,01см) на плане, называется предельной точностью масштаба.

Практически принимается, что длина отрезка на плане или карте может быть оценена с точностью 0,2 мм.

Горизонтальное расстояние на местности, соответствующее в данном масштабе 0,2 мм (0,02 см) на плане, называется графической точностью масштаба.

Значения предельной и графической точностей различных числен­ных масштабов, найденные по формулам (17) и (18), приведены ниже.

Такая точность определения расстояний на плане или карте не мо­жет быть достигнута при использовании линейного масштаба. Поэто­му для повышения точности измерений расстояний на плане или карте применяют поперечный (трансверсальный)масштаб.

2. Масштаб— это отношение длины линии на чертеже, плане, карте l к длине горизонтального проложения, соответствующей линии местности S:

М = l/ S.

При выполнении съемок, составлении геодезических чертежей и при работе с ними приходится пользоваться следующими видами масштабов: численным, пояснительным, линейным, поперечным, переводным.

Численным горизонтальным масштабом называется отношение длины линии, взятой на чертеже, к длине той же линии, взятой на проекции, т.е. на уровенной поверхности или на горизонтальной плоскости.

На профилях различают еще вертикальный численный масштаб, относящийся к высотным элементам проекции.

3. Численный масштаб записывают в виде правильной дроби, у которой числитель единица, а знаменатель показывает степень уменьшения линейных размеров на плане. В метрической системе мер пользуются такими масштабами: 1:500, 1:1000, 1:2000, 1:5000, 1:10 000 и т.д. При сравнении двух или нескольких масштабов между собой надо иметь в виду, что чем больше знаменатель, тем, крупнее масштаб плана, и на таком плане изобразится больше мелких деталей, а измерение линий по нему можно сделать с большей точностью. Следовательно, масштаб 1:5000 крупнее 1:10 000, но мельче 1:2000. Например, численный масштаб 1:1000 показывает, что все горизонтальные проложения линий местности при перенесении их на план уменьшены в 1000 раз, то есть отрезок в 1 см на плане соответствует линии в 1000 см (10 м) на местности

Пример 1: Длина линии на плане масштаба 1:5000 равна 4 см. Определить ее длину на местности. Решение: 4х5000=20000 см = 200 м.

Пример 2: Если горизонтальное проложение линии местности равно 283,7 м, масштаб 1:5000, т.е. в сантиметре 50 м, то длина линии на плане будет 283,7:50 = 5,67 см.

4. Линейный масштаб представляет собой шкалу, деления которой подписаны применительно к заданному численному масштабу. Им пользуются при нанесении проекции линий на чертеж, а также при измерении линий на чертеже с целью определения соответствующей им длины на проекции. Применение линейного масштаба избавляет от вычислений, выполняемых при пользовании численным масштабом. Хотя эти вычисления просты, но при большом их количестве становятся утомительными и отнимают много времени.

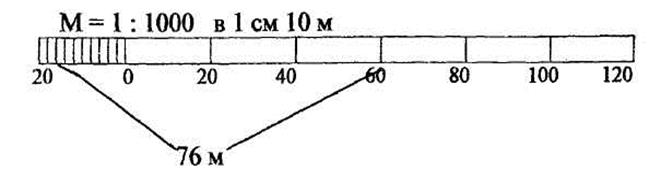
Рисунок 1 – Линейный масштаб

Для построения метрического линейного масштаба берут прямую линию и откладывают на ней несколько раз (четыре-пять) один и тот же отрезок (1-2 см), называемый основанием масштаба (рис.1). Первое основание делят на 10 равных частей и на правом конце его пишут нуль, а на левом – то число метров или километров, которое на проекции соответствует в заданном масштабе основанию. Вправо от нуля деления масштаба подписывают соответственно расстояниям на местности, выраженным отрезками от нуля до штриха с подписью. В качестве основания для метрических масштабов чаще всего берут отрезок в 2 см. При работе в масштабе 1:1000 и основании, равном 2 см, линейный масштаб подписывают так, как это указано на рис. 1.

При этом масштабе 2 см на бумаге соответствует 2000 см или 20 м на местности, а 1 см — соответственно 1000 см или 10 м.

При пользовании линейным масштабом правую ножку циркуля ставят на нулевое деление или на одно из делений справа от нуля в зависимости от того, меньше или больше одного основания нужно измерить или отложить линию. Левая ножка циркуля располагается либо на делении с нулевой подписью, если длина линии содержит целое число оснований, либо в пределах первого основания, имеющего мелкие деления, с оценкой на глаз десятых долей этих делений. По горизонтальным размерным линиям легко сообразить, где находились ножки циркуля, когда брали тот или иной отрезок. Видно также, что каждый отрезок составляется из двух частей: от нуля до правой ножки циркуля и от нуля до левой ножки его.

При откладывании с помощью измерителя круглых чисел 20, 40 м и т. д. одна ножка измерителя устанавливается на нулевое деление, а вторая — на деление с соответствующей надписью. Каждое деление первого основания слева равно: 20 м : 10 = 2 м. Чтобы отложить, например, 76 м, надо одну ножку измерителя поставить на деление 60, а вторую на восьмое деление от нуля слева (8 х 2 м = 16 м). В итоге получается: 60 м + 16 м = 76 м. Десятые доли метра определяются на глаз (рис. 1).

Применение простого линейного масштаба ограничено вследствие сравнительно небольшой его точности, поэтому для составления точных планов и карт пользуются преимущественно поперечным масштабом.

5. Поперечный масштаб применяют для того, чтобы избежать оценки на глаз долей делений первого основания и в результате повысить точность измерений и построений на чертежах. Обычно пользуются поперечными

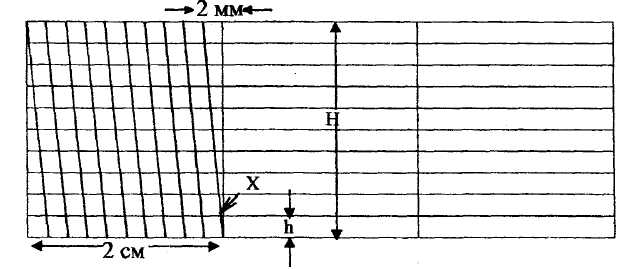Рисунок 2 – Поперечные масштаб

масштабами, награвированными на тонких металлических пластинках или на транспортирах. Поперечный масштаб строится в виде прямоугольника длиной 8-10 см и высотой 2-3 см. В случае надобности поперечный масштаб для заданного численного можно построить (рис.2) следующим образом.

На горизонтальной прямой, как и при построении линейного масштаба, откладывают несколько раз основание (6-10 отрезков, обычно 2 см) и первый отрезок делят на 10 равных частей (обычно в 2 мм). Полученные деления подписывают подобно тому, как это делалось при построении линейного масштаба. Из концов всех оснований проводят вверх вертикальные линии; на крайних линиях откладывают по 10 одинаковых отрезков, например, по 2 мм каждый; полученные в результате этого точки соединяют горизонтальными прямыми. Верхнюю линию первого основания делят на десять равных частей и к ранее нанесенным делениям внизу, на первом основании, проводят косые линии, называемые трансверсалями, как показано на рис.2. Между косыми параллельными линиями заключены горизонтальные отрезки, равные десятой доле основания каждой в отдельности. Между нулевой вертикальной линией и смежной с ней косой линией заключаются отрезки от одной до десяти десятых наименьшего деления основания или от одной до десяти сотых самого основания, т.е. как раз то, что приходится отсчитывать на глаз по линейному масштабу. Значение мелких делений подписано у крайней левой вертикальной линии масштаба, что облегчает пользование им.

Основание самого большого треугольника равно 2 мм. Основание (Х) самого маленького треугольника называется наименьшим делением поперечного масштаба.

Если высоту большого треугольника обозначить буквой Н, а маленького треугольника h, то из соотношения 2/Н=Х/h, получается, что

Х=(2· h)/Н; но h=Н/10,

тогда Х=(2·Н)/(Н·10)=0,2 мм

Каждая от откладываемых по масштабу линий слагается из трех частей:

1) количества целых основания, взятых от нулевой вертикальной линии до правой ножки циркуля;

2) десятых долей основания, взятых между косыми линиями от проходящей через нуль до левой ножки циркуля;

3) сотых долей основания, расположенных между вертикальной и косой линиями, выходящими из нулевой точки масштаба.

Пользуясь поперечным масштабом, нужно следить за тем, чтобы при отложении или измерении отрезка концы обеих ножек циркуля всегда находились на одной и той же горизонтальной линии масштаба.

Масштабы, награвированные на пластинках или на транспортирах, следует разметить соответственно тому численному масштабу, в котором составлен или будет составляться чертеж.

Предельной точностью масштаба называется отрезок на проекции местности, который соответствует наименьшему делению поперечного масштаба, т.е. одной сотой основания его. Наименьшее деление поперечного масштаба равно 0,2 мм или 1/100 основания масштаба.

Дата добавления: 2015-02-13 ; просмотров: 8571 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник