Как начертить наклонную пятиугольную призму
Как нарисовать пятиугольную призму? Объем и площадь поверхности фигуры
Пятиугольная призма при решении задач по геометрии встречается гораздо реже, чем такие призмы, как треугольная, четырехугольная или шестиугольная. Тем не менее полезно рассмотреть основные свойства этой фигуры, а также узнать, как ее можно нарисовать.
Что собой представляет пятиугольная призма?
Если пятиугольник будет правильным, то есть все его стороны и углы будут равны друг другу, тогда такая прямоугольная призма называется правильной. Далее в статье будем рассматривать свойства именно этой фигуры.
Элементы призмы
Для нее, как и для любой призмы, характерны следующие элементы:
Числа всех названных элементов связаны друг с другом следующим равенством:
Это выражение носит название формулы Эйлера для полиэдра.
В пятиугольной призме количество сторон равно семи (два основания + пять прямоугольников). Число вершин составляет 10 (по пять для каждого основания). Число ребер в таком случае будет равно:
Десять ребер принадлежат основаниям призмы, а пять ребер образованы прямоугольниками.
Как начертить пятиугольную призму?
Ответ на этот вопрос зависит от конкретной задачи. Если необходимо начертить произвольную призму, тогда следует изобразить любой пятиугольник. После этого провести пять параллельных отрезков равной длины из каждой вершины пятиугольника. Затем, соединить верхние концы отрезков. Получилась пятиугольная произвольная призма.
Если же следует начертить правильную призму, тогда вся сложность задачи сводится к получению правильного пятиугольника. Существует несколько способов начертить этот многоугольник. Здесь мы рассмотрим только два способа.
Первый способ заключается в построении окружности с помощью циркуля. Затем проводится произвольный диаметр окружности и от него отсчитывается с помощью транспортира пять углов по 72o (5*72o = 360o). При отсчете каждого угла делается насечка на окружности. Для построения прямоугольника остается соединить прямыми отрезками отмеченные насечки.
Второй способ предполагает использование только циркуля и линейки. Он является несколько сложным в сравнении с предыдущим. Ниже приводится видео, где подробно объясняется каждый шаг такого построения.
Заметим, что пятиугольник легко нарисовать, если соединить концы звезды. Если нет необходимости чертить точно правильный пятиугольник, тогда можно использовать способ со звездой, нарисованной от руки.
Как только пятиугольник изображен, следует из каждой его вершины провести пять одинаковых параллельных отрезков и соединить их вершины. Получится пятиугольная призма.
Площадь фигуры
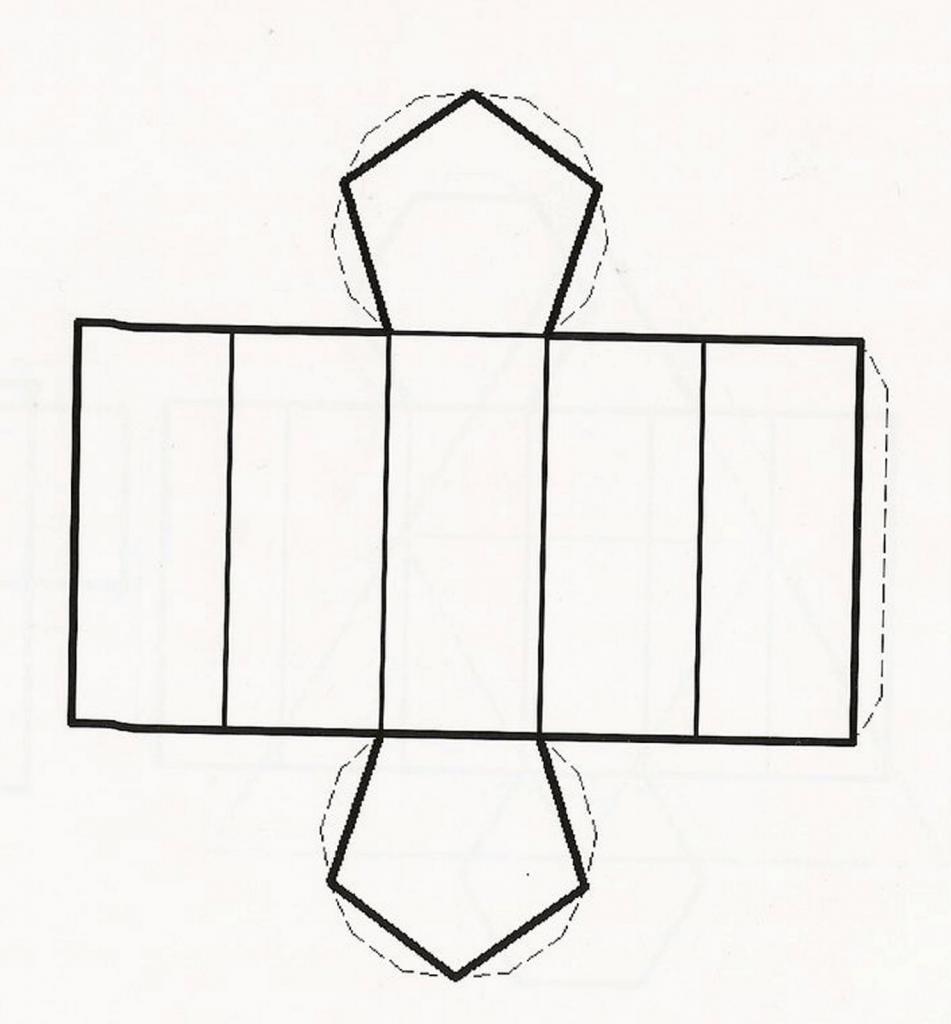
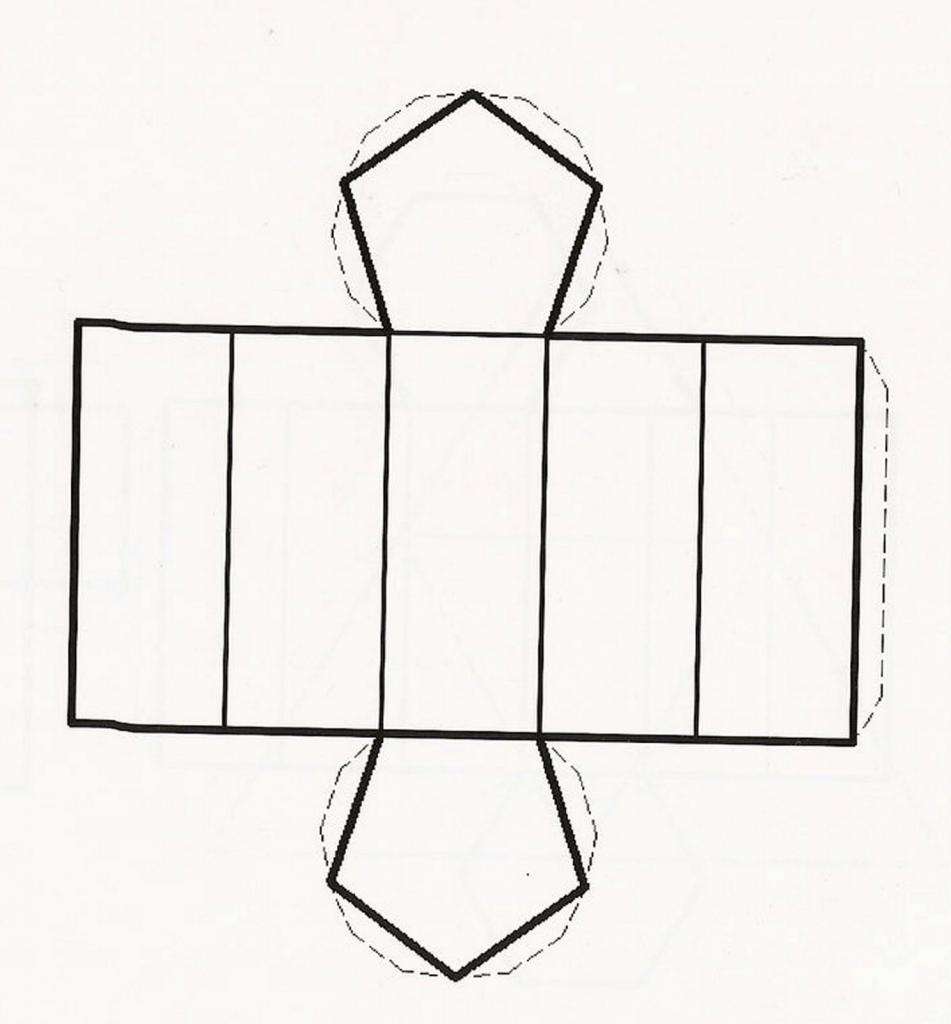
Теперь рассмотрим вопрос, как найти площадь пятиугольной призмы. На рисунке ниже приведена ее развертка. Видно, что искомая площадь образована двумя одинаковыми пятиугольниками и пятью равными друг другу прямоугольниками.
Площадь всей поверхности фигуры выразится формулой:
Здесь индексы o и p означают основание и прямоугольник соответственно. Обозначим длину стороны пятиугольника как a, а высоту фигуры как h. Тогда для прямоугольника запишем:
Чтобы вычислить площадь пятиугольника, воспользуемся универсальной формулой:
S5 = 5/4*a2*ctg(pi/5) ≈ 1,72*a2
Точность полученного равенства составляет 3 знака после запятой, что вполне достаточно для решения любых задач.
Теперь остается найти сумму полученных площадей основания и боковой поверхности. Имеем:
S = 2*1,72*a2 + 5*a*h = 3,44*a2 + 5*a*h
Следует помнить, что полученная формула справедлива только для прямоугольной призмы. В случае с косоугольной фигурой площадь ее боковой поверхности находят, исходя из знания периметра среза, который должен быть перпендикулярен всем параллелограммам.
Объем фигуры
Формула расчета объема пятиугольной призмы ничем не отличается от аналогичного выражения для любой другой призмы или цилиндра. Объем фигуры равен произведению ее высоты на площадь основания:
Если рассматриваемая призма является прямоугольной, тогда высота в ней является длиной ребра, образованного прямоугольниками. Площадь правильного пятиугольника была вычислена выше с высокой точностью. Подставим это значение в формулу для объема и получим необходимое выражение для пятиугольной правильной призмы:
Таким образом, вычисление объема и площади поверхности пятиугольной правильной призмы возможно, если известна сторона основания и высота фигуры.
Правильная пятиугольная призма
Пятиугольная призма — это многогранник, две грани которого являются равными пятиугольниками, лежащими в параллельных плоскостях, а остальные грани (боковые грани) — параллелограммами, имеющими общие стороны с этими пятиугольниками.
Основания призмы являются равными правильными пятиугольниками.
Боковые грани призмы являются прямоугольниками.
Боковые рёбра призмы параллельны и равны.
Размеры призмы можно выразить через длину стороны a и высоту h.
Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания.
Формула площади поверхности пятиугольной призмы:
Пятиугольная призма: характеристики, детали, вершины, ребра, объем
Содержание:
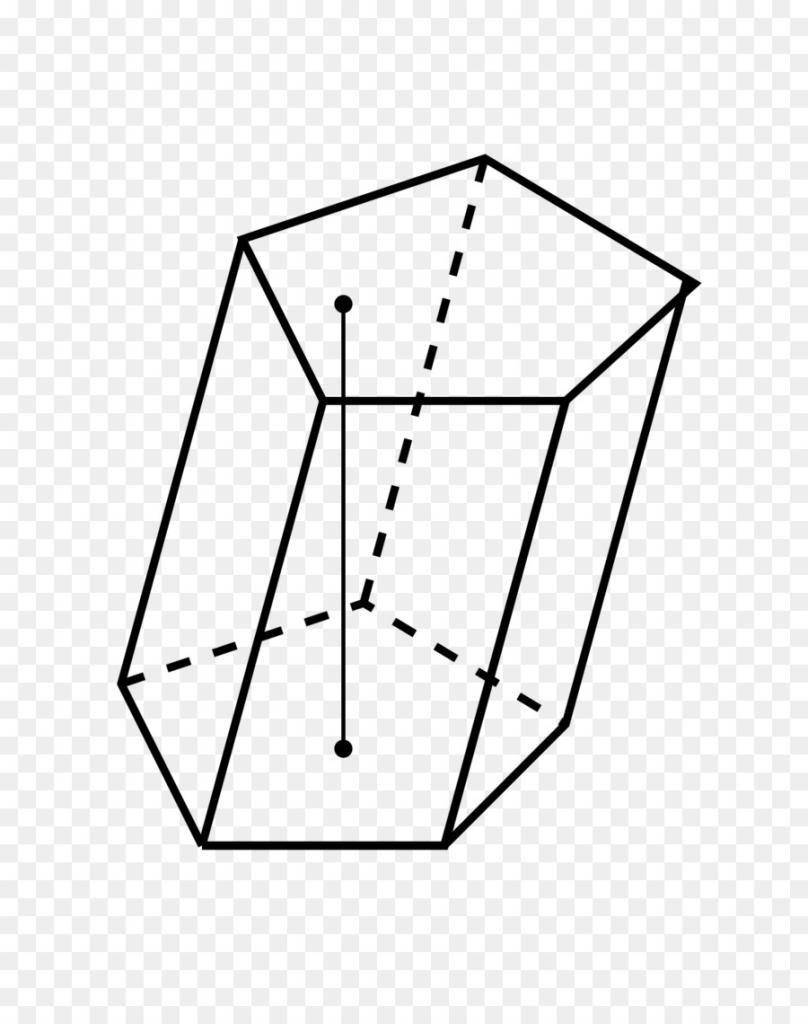
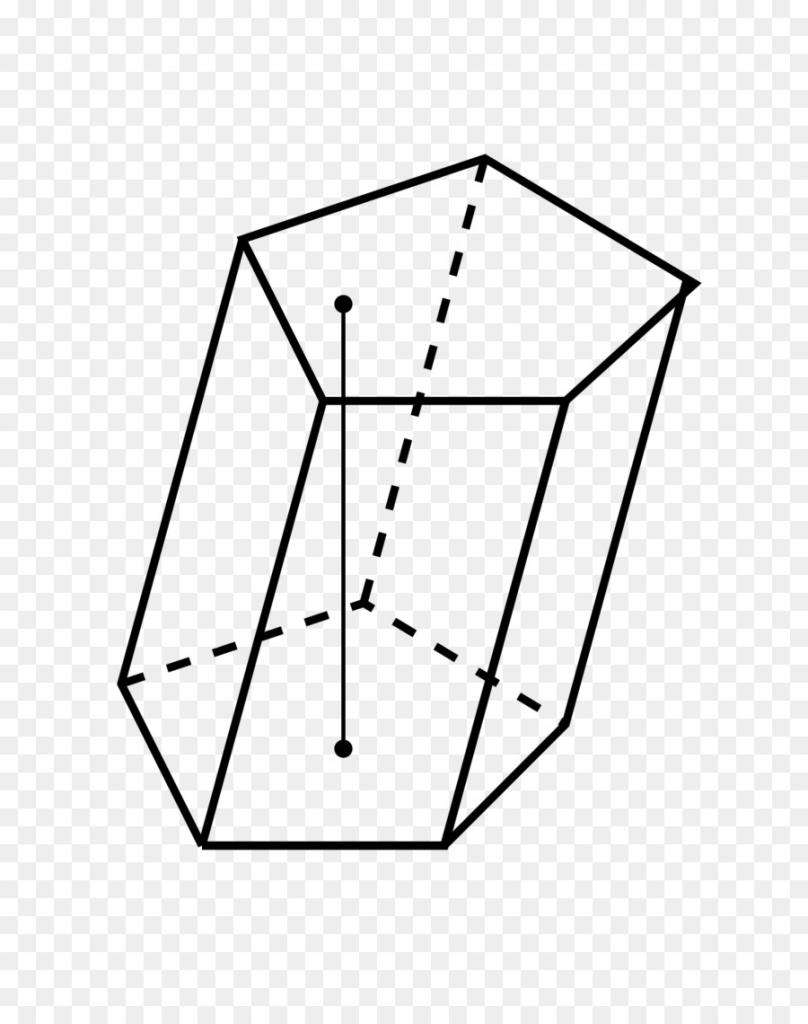
А пятиугольная призма Это трехмерная геометрическая фигура, основания которой идентичны, имеют форму пятиугольника, а также имеют в общей сложности 5 граней в форме параллелограмма.
Если грани прямоугольные, это называется правая пятиугольная призма, а если ребра наклонены относительно оснований, то это наклонная пятиугольная призма. На изображении ниже показан пример каждого из них.
Базовый пятиугольник может быть правильным, если его пять сторон имеют одинаковую меру, а также внутренние углы, в противном случае это неправильный пятиугольник. Если основание призмы правильное, оноправильная пятиугольная призма. В противном случае это призма пятиугольный неправильный.
Характеристики пятиугольной призмы
-Это трехмерная геометрическая фигура, поверхности, составляющие ее, заключают в себе определенный объем.
-У него есть вершины-углы призмы- и ребра-ребра или ребра-.
-Если кромки, соединяющие основания, перпендикулярны им, призма прямая, а если они наклонены, призма наклонная.
-Когда основание представляет собой пятиугольник с внутренними углами менее 180 °, призма выпуклый, но если один или несколько внутренних углов больше 180 °, это призма вогнутый.
Элементы пятиугольной призмы
–Лица: пятиугольная призма имеет в общей сложности 7 граней: два пятиугольных основания и пять параллелограммов, составляющих стороны.
–Край: сегмент, соединяющий две базы, показанный красным на рисунке 3, или тот, который соединяет две стороны.
–Высота: расстояние между гранями. Если призма прямая, это расстояние соответствует размеру края.
–Вершина: точка пересечения основания и двух боковых граней.
На рисунке ниже показана правая пятиугольная призма с правильным основанием, в которой сегменты, образующие основание, имеют одинаковую меру, называемую к.
Этот тип призмы также имеет следующие элементы, характерные для правильного пятиугольника:
–Радиус R: расстояние между центром пятиугольника и одной из вершин.
–Апофема LК: сегмент, соединяющий центр со средней точкой одной из сторон пятиугольника.
Сколько вершин у пятиугольной призмы?
В пятиугольнике 5 вершин, и поскольку у пятиугольной призмы есть два пятиугольника в качестве основания, у этого тела всего 10 вершин.
Сколько граней у пятиугольной призмы?
Теорема устанавливает связь между количеством граней, которые мы будем называть C, количеством вершин V и общим количеством ребер A следующим образом:
Для пятиугольной призмы имеем: C = 7 и V = 10. Решая относительно A, количество ребер:
Пятиугольная призма имеет 15 граней.
Как найти объем пятиугольной призмы?
Объем пятиугольной призмы измеряет пространство, ограниченное сторонами и основаниями. Это положительная величина, которая рассчитывается по следующему свойству:
Любая плоскость, которая разрезает призму перпендикулярно ее краям, создает пересечение той же формы, что и основание, то есть пятиугольник тех же размеров.
Следовательно, объем пятиугольной призмы является произведением площади основания и высоты призмы.
Быть КB площадь пятиугольного основания и час высота призмы, затем объем V это:
Эта формула носит общий характер и действительна для любой призмы, будь то правильная или неправильная, прямая или наклонная.
— Объем обычной пятиугольной призмы
В правильной пятиугольной призме основания представляют собой правильные пятиугольники, что означает, что стороны и внутренние углы равны. Учитывая симметрию тела, площадь пятиугольника и, следовательно, объем легко вычисляется несколькими способами:
Зная высоту и размер стороны
Быть к размер стороны пятиугольного основания. В этом случае площадь рассчитывается по:
Следовательно, объем правильной пятиугольной призмы высоты h равен:
Зная высоту и радиус измерения
Когда радиус R Пятиугольного основания, это другое уравнение можно использовать для площади основания:
А = (5/2) R 2 ⋅ грех 72º
Таким образом, объем пятиугольной призмы определяется как:
V = (5/2) R 2 ⋅ ч ⋅ грех 72º
куда час это высота призмы
Зная высоту, меру апофемы и значение периметра
Площадь пятиугольного основания может быть вычислена, если известен его периметр P, который представляет собой просто сумму сторон, а также меру апофемы L.К:
Умножая это выражение на значение высоты час, имеем объем призмы:
— Объем неправильной пятиугольной призмы
Формула, приведенная в начале, действительна даже тогда, когда основание призмы представляет собой неправильный пятиугольник:
Для расчета площади основания используются разные методы, например:
-Метод триангуляции, который состоит из деления пятиугольника на треугольники и четырехугольники, соответствующие площади которых легко вычисляются. Площадь пятиугольника будет суммой площадей этих более простых фигур.
-Метод определения гауссовских определителей, для которого необходимо знать вершины фигуры.
Как только значение площади определено, оно умножается на высоту призмы для получения объема.
Как нарисовать пятиугольную призму? Объем и площадь поверхности фигуры
Пятиугольная призма при решении задач по геометрии встречается гораздо реже, чем такие призмы, как треугольная, четырехугольная или шестиугольная. Тем не менее полезно рассмотреть основные свойства этой фигуры, а также узнать, как ее можно нарисовать.
Что собой представляет пятиугольная призма?
Если пятиугольник будет правильным, то есть все его стороны и углы будут равны друг другу, тогда такая прямоугольная призма называется правильной. Далее в статье будем рассматривать свойства именно этой фигуры.
Элементы призмы
Для нее, как и для любой призмы, характерны следующие элементы:
Числа всех названных элементов связаны друг с другом следующим равенством:
Это выражение носит название формулы Эйлера для полиэдра.
В пятиугольной призме количество сторон равно семи (два основания + пять прямоугольников). Число вершин составляет 10 (по пять для каждого основания). Число ребер в таком случае будет равно:
Десять ребер принадлежат основаниям призмы, а пять ребер образованы прямоугольниками.
Как начертить пятиугольную призму?
Ответ на этот вопрос зависит от конкретной задачи. Если необходимо начертить произвольную призму, тогда следует изобразить любой пятиугольник. После этого провести пять параллельных отрезков равной длины из каждой вершины пятиугольника. Затем, соединить верхние концы отрезков. Получилась пятиугольная произвольная призма.
Если же следует начертить правильную призму, тогда вся сложность задачи сводится к получению правильного пятиугольника. Существует несколько способов начертить этот многоугольник. Здесь мы рассмотрим только два способа.
Первый способ заключается в построении окружности с помощью циркуля. Затем проводится произвольный диаметр окружности и от него отсчитывается с помощью транспортира пять углов по 72o (5*72o = 360o). При отсчете каждого угла делается насечка на окружности. Для построения прямоугольника остается соединить прямыми отрезками отмеченные насечки.
Второй способ предполагает использование только циркуля и линейки. Он является несколько сложным в сравнении с предыдущим. Ниже приводится видео, где подробно объясняется каждый шаг такого построения.
Заметим, что пятиугольник легко нарисовать, если соединить концы звезды. Если нет необходимости чертить точно правильный пятиугольник, тогда можно использовать способ со звездой, нарисованной от руки.
Как только пятиугольник изображен, следует из каждой его вершины провести пять одинаковых параллельных отрезков и соединить их вершины. Получится пятиугольная призма.
Площадь фигуры
Теперь рассмотрим вопрос, как найти площадь пятиугольной призмы. На рисунке ниже приведена ее развертка. Видно, что искомая площадь образована двумя одинаковыми пятиугольниками и пятью равными друг другу прямоугольниками.
Площадь всей поверхности фигуры выразится формулой:
Здесь индексы o и p означают основание и прямоугольник соответственно. Обозначим длину стороны пятиугольника как a, а высоту фигуры как h. Тогда для прямоугольника запишем:
Чтобы вычислить площадь пятиугольника, воспользуемся универсальной формулой:
S5 = 5/4*a2*ctg(pi/5) ≈ 1,72*a2
Точность полученного равенства составляет 3 знака после запятой, что вполне достаточно для решения любых задач.
Теперь остается найти сумму полученных площадей основания и боковой поверхности. Имеем:
S = 2*1,72*a2 + 5*a*h = 3,44*a2 + 5*a*h
Следует помнить, что полученная формула справедлива только для прямоугольной призмы. В случае с косоугольной фигурой площадь ее боковой поверхности находят, исходя из знания периметра среза, который должен быть перпендикулярен всем параллелограммам.
Объем фигуры
Формула расчета объема пятиугольной призмы ничем не отличается от аналогичного выражения для любой другой призмы или цилиндра. Объем фигуры равен произведению ее высоты на площадь основания:
Если рассматриваемая призма является прямоугольной, тогда высота в ней является длиной ребра, образованного прямоугольниками. Площадь правильного пятиугольника была вычислена выше с высокой точностью. Подставим это значение в формулу для объема и получим необходимое выражение для пятиугольной правильной призмы:
Таким образом, вычисление объема и площади поверхности пятиугольной правильной призмы возможно, если известна сторона основания и высота фигуры.
Как научиться правильно изображать призму
Главная страница » Основы Академического рисунка » Как построить призму. Правильное изображение фигуры на рисунке
Овладеть базовыми знаниями в области рисунка необходимо каждому начинающему художнику, независимо от выбранного стиля живописи. Обучение рисунку происходит поэтапно, и одной из важнейших тем является построение геометрических фигур. Сначала ученики осваивают плоские объекты, а потом переходят к объемным – в частности, призмам.
В зависимости от фигуры, лежащей в основании, призма бывает треугольной, четырехугольной, пятиугольной и так далее. Рассмотрим процесс рисования на примере четырехгранной и шестигранной призмы.
Рисуем четырехгранную призму
Четырехгранная призма строится по тому же плану, что и куб, поэтому логично сначала освоить рисование этой фигуры. Обе они – это простые геометрические тела, имеющие прямые грани. Однако если у куба все грани являются квадратами, то у призмы квадраты – это только основания, а боковые грани – прямоугольники.
Объект рисуют в точности так же, как и куб, длина которого затем увеличивается по горизонтали или вертикали (в зависимости от положения предмета).
Как правило, длина увеличивается в полтора раза, однако это зависит от того, во сколько раз высота фигуры превышает ширину основания призмы.
Сначала нужно нанести на лист бумаги общие габариты фигуры при помощи легких линий карандашом.
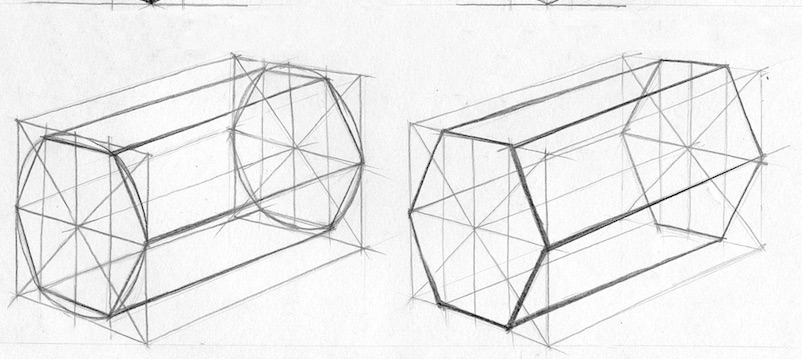
Шестигранная призма
Основой для построения шестигранной призмы является четырехгранная. Передняя поверхность делится пополам по вертикали и горизонтали с учетом перспективы, если тело изображено в ракурсе. Затем вписываем в поверхность эллипс. Горизонтальная ось, пересекающая поверхность, делится еще раз пополам с учетом перспективы. Ставим точки в местах пересечения получившихся вертикалей с окружностью. Соединяем их между собой и с углами.
Точно такой же шестиугольник нужно нарисовать на задней стороне четырехгранной призмы, а затем соединить его с первым нарисованным шестиугольником. Таким образом, у нас получится шестигранная призма, вписанная в четырехгранную.
Чтобы показать объем вашей призмы, нужно обозначить светотени. В первую очередь нужно заштриховать поверхности в тени и те, на которые тень падает. После этого нужно проработать самые освещенные поверхности.
Зачем уметь строить эту геометрическую фигуру?
Научиться изображать геометрические тела, в том числе и призмы, необходимо всем будущим художникам.
С построения этих объектов начинается учебный процесс во всех заведениях. А уже после этого студенты постепенно переходят к изображению розеток, капителей, портрета и фигуры человека.
Если вы освоите этот объект, то в дальнейшем вам будет проще изображать различные предметы, строящиеся на его основе. В частности, у вас не возникнет трудностей с различными коробками и упаковками, бытовой техникой, зданиями и так далее.
Рисование геометрических тел также входит и в экзаменационную программу для поступления в художественный вуз. Однако с первого раза построить правильную фигуру с соблюдением пропорции и перспективы получается далеко не у каждого. Поэтому будет лучше, если в процессе подготовки к экзаменам вы потратите на изображение призмы достаточно времени, тогда на самом вступительном испытании будете чувствовать себя уверенно. С каждым разом изображение призмы будет даваться все легче.
В школе-студии К.Э. Арутюновой «Мастер рисунка» учат работать с геометрическими телами. К каждому ученику применяется индивидуальный подход с учетом его уровня и времени до сдачи вступительного экзамена. Преподаватель подробно разбирает со студентами все работы, обращает внимание на ошибки и помогает их исправить.
Готовитесь ли вы к поступлению в художественный вуз или просто хотите научиться для себя, без основ вам не обойтись. Независимо от того, в каком стиле вы собираетесь работать позднее, начать изучение все равно необходимо с базовых знаний. Запишитесь на занятия по телефону в Москве или через специальную форму на сайте.