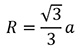Как начертить призму в геометрии
Как научиться правильно изображать призму
Старт освоения рисунка и живописи всегда начинается с академического рисунка. Именно это те основы, которые помогают потом создавать картины разной сложности и в разных техниках. Академический рисунок — длительный и постепенный процесс. Начало изучения заключается в рисовании простых геометрических фигур, чаще всего ими выступают гипсовые фигуры. Построение геометрических предметов помогают в дальнейшем реализовывать даже самые сложные задачи. Из простых форм всегда изучают куб, после чего переходят к призмам. Призмы бывают разные, форма зависит от того, как фигура лежит в основании — четырехугольник, пятиугольник и т.д. Сегодня мы расскажем, как правильно изображать призму на разных примерах.
Как правильно изобразить четырехгранную призму?
Процесс построения призмы схожий с построением куба, поэтому, если вы справились с данной фигурой, то рисунок четырехгранной призмы будет простым и легким. Схожесть этих фигур — у них обеих прямые грани. У куба все грани квадраты, а у призмы — только основы. Боковые грани — это прямоугольники.
Первым шагом намечаем композицию легкими линиями, затем рисуем основание призмы и уже от произвольной длины основы мы можем измерять высоту призмы. Для того, чтобы понять, какое соотношение сторон, мы можем использовать карандаш на вытянутой руке. Стоит помнить о том, что раскрытие верхнего квадрата будет меньше, нежели раскрытие ниже. Это правило работает, если предмет находится ниже линии горизонта. Нам следует рисовать точные линии, чтобы точки пересечения были четкими. Аккуратность построения будет влиять на то, насколько проработанным будет итоговое изображение.
Как правильно изобразить шестигранную призму?
Шестигранная призма строится уже значительно сложнее. Можно идти по принципу построения четырехгранной призмы, где сначала обозначается основа, а затем достраиваются боковые грани. Можно строить иначе. Для того, чтобы правильно построить шестигранную призму, мы должны построить четырехгранную.
При этом мы делим переднюю грань пополам, создавая дополнительные грани. Этот способ сложнее, так как ошибка на первом этапе может испортить итоговый результат. Шестигранную призму мы строим с применениями знаний о раскрытии эллипсов, что способствует правильному определению размеров граней. Как и любой предмет, объемность призмы создается с помощью светотени. Начинаем штриховку равномерно, после чего добираем тон в самых темных участках.
Для чего необходимо уметь строить призму?
Призма помогает закрепить знания по рисунку фигур с плоскими формами. При этом закрепляется целый ряд тем и техник. Происходит знакомство с понятием “раскрытие”, оттачивается мастерство аккуратного построения и измерения предметов.
Призма позволяет отработать умения, чтобы научиться изображать реальные предметы, здания, коробки.
Правильная треугольная призма
Треугольная призма — это многогранник,две грани которого являются равными треугольниками, лежащими в параллельных плоскостях, а остальные грани (боковые грани) — параллелограммами, имеющими общие стороны с этими треугольниками.
Основания призмы являются равными правильными треугольниками.
Боковые грани призмы являются прямоугольниками.
Боковые рёбра призмы параллельны и равны.
Размеры призмы можно выразить через длину стороны a и высоту h.
Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания.
Формула площади поверхности треугольной призмы:
Объём призмы равен произведению её высоты на площадь основания.
Формула объема правильной треугольной призмы:
Правильная треугольная призма может быть вписана в цилиндр.
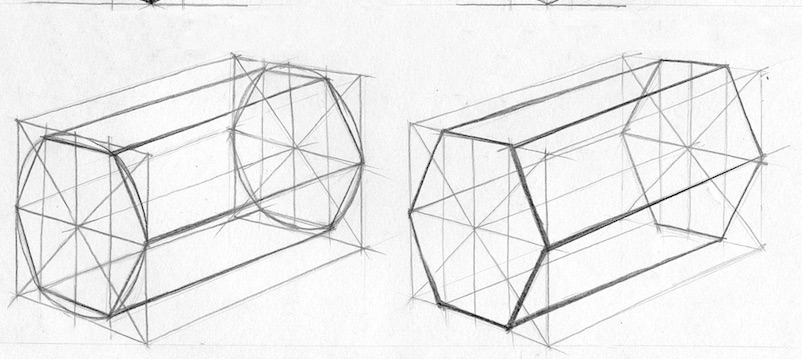
Формула радиуса цилиндра вписанной треугольной призмы:
Анимация демонстрирует как две параллельные плоскости отрезая лишнее формируют два основания призмы. Из одной заготовки можно получить как правильную призму, так и наклонную призму.
Как научиться правильно изображать призму
Главная страница » Основы Академического рисунка » Как построить призму. Правильное изображение фигуры на рисунке
Овладеть базовыми знаниями в области рисунка необходимо каждому начинающему художнику, независимо от выбранного стиля живописи. Обучение рисунку происходит поэтапно, и одной из важнейших тем является построение геометрических фигур. Сначала ученики осваивают плоские объекты, а потом переходят к объемным – в частности, призмам.
В зависимости от фигуры, лежащей в основании, призма бывает треугольной, четырехугольной, пятиугольной и так далее. Рассмотрим процесс рисования на примере четырехгранной и шестигранной призмы.
Рисуем четырехгранную призму
Четырехгранная призма строится по тому же плану, что и куб, поэтому логично сначала освоить рисование этой фигуры. Обе они – это простые геометрические тела, имеющие прямые грани. Однако если у куба все грани являются квадратами, то у призмы квадраты – это только основания, а боковые грани – прямоугольники.
Объект рисуют в точности так же, как и куб, длина которого затем увеличивается по горизонтали или вертикали (в зависимости от положения предмета).
Как правило, длина увеличивается в полтора раза, однако это зависит от того, во сколько раз высота фигуры превышает ширину основания призмы.
Сначала нужно нанести на лист бумаги общие габариты фигуры при помощи легких линий карандашом.
Шестигранная призма
Основой для построения шестигранной призмы является четырехгранная. Передняя поверхность делится пополам по вертикали и горизонтали с учетом перспективы, если тело изображено в ракурсе. Затем вписываем в поверхность эллипс. Горизонтальная ось, пересекающая поверхность, делится еще раз пополам с учетом перспективы. Ставим точки в местах пересечения получившихся вертикалей с окружностью. Соединяем их между собой и с углами.
Точно такой же шестиугольник нужно нарисовать на задней стороне четырехгранной призмы, а затем соединить его с первым нарисованным шестиугольником. Таким образом, у нас получится шестигранная призма, вписанная в четырехгранную.
Чтобы показать объем вашей призмы, нужно обозначить светотени. В первую очередь нужно заштриховать поверхности в тени и те, на которые тень падает. После этого нужно проработать самые освещенные поверхности.
Зачем уметь строить эту геометрическую фигуру?
Научиться изображать геометрические тела, в том числе и призмы, необходимо всем будущим художникам.
С построения этих объектов начинается учебный процесс во всех заведениях. А уже после этого студенты постепенно переходят к изображению розеток, капителей, портрета и фигуры человека.
Если вы освоите этот объект, то в дальнейшем вам будет проще изображать различные предметы, строящиеся на его основе. В частности, у вас не возникнет трудностей с различными коробками и упаковками, бытовой техникой, зданиями и так далее.
Рисование геометрических тел также входит и в экзаменационную программу для поступления в художественный вуз. Однако с первого раза построить правильную фигуру с соблюдением пропорции и перспективы получается далеко не у каждого. Поэтому будет лучше, если в процессе подготовки к экзаменам вы потратите на изображение призмы достаточно времени, тогда на самом вступительном испытании будете чувствовать себя уверенно. С каждым разом изображение призмы будет даваться все легче.
В школе-студии К.Э. Арутюновой «Мастер рисунка» учат работать с геометрическими телами. К каждому ученику применяется индивидуальный подход с учетом его уровня и времени до сдачи вступительного экзамена. Преподаватель подробно разбирает со студентами все работы, обращает внимание на ошибки и помогает их исправить.
Готовитесь ли вы к поступлению в художественный вуз или просто хотите научиться для себя, без основ вам не обойтись. Независимо от того, в каком стиле вы собираетесь работать позднее, начать изучение все равно необходимо с базовых знаний. Запишитесь на занятия по телефону в Москве или через специальную форму на сайте.
Линейно-конструктивный рисунок шестигранной призмы
ЦЕЛЬ ЗАДАНИЯ. Научиться изображать шестигранную призму в различных положениях.
ПОСТАНОВКА ЗАДАНИЯ. Изучите различные способы построения правильного шестиугольника, сделайте рисунки шестиугольников, проверьте правильность их построения. На основе шестиугольников постройте шестигранные призмы.
РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ ЗАДАНИЯ.
Рассмотрите шестигранную призму на рис. 3.52 и ее ортогональные проекции на рис. 3.53. В основании шестигранной призмы (шестигранника) лежат правильные шестиугольники, боковые грани — одинаковые прямоугольники. Для того, чтобы правильно изобразить шестигранник в перспективе, необходимо сначала научиться грамотно изображать в перспективе его основание (рис. 3.54). В шестиугольнике на рис. 3.55 вершины обозначены цифрами от одного до шести.
Если соединить точки 1 и 3, 4 и 6 вертикальными прямыми, можно заметить, что эти прямые вместе с точкой центра окружности делят диаметр 5— 2 на четыре равных отрезка (эти отрезки обозначены дугами). Противоположные стороны шестиугольника параллельны друг другу и прямой, проходящей через его центр и соединяющей две вершины (например, стороны 6— 1 и 4— 3 параллельны прямой 5— 2). Эти наблюдения помогут вам построить шестиугольник в перспективе, а также проверить правильность этого построения.
Построить правильный шестиугольник по представлению можно двумя способами: на основе описанной окружности и на основе квадрата.
На основе описанной окружности. Рассмотрите рис. 3.56. Все вершины правильного шестиугольника принадлежат описанной окружности, радиус которой равен стороне шестиугольника.
Горизонтальный шестиугольник
Изобразите горизонтальный эллипс произвольного раскрытия, т.е. описанную окружность в перспективе. Теперь необходимо найти на ней шесть точек, являющихся вершинами шестиугольника. Проведите любой диаметр данной окружности через ее центр (рис. 3.57).
Крайние точки диаметра — 5 и 2, лежащие на эллипсе, являются вершинами шестиугольника. Для нахождения остальных вершин необходимо разделить этот диаметр на четыре одинаковых отрезка. Диаметр уже разделен точкой центра окружности на два радиуса, остается разделить каждый радиус пополам. На перспективном рисунке все четыре отрезка равномерно сокращаются при удалении от зрителя (рис. 3.58). Теперь проведите через середины радиусов — точки А и В — прямые, перпендикулярные прямой 5— 2. Найти их направление можно при помощи касательных к эллипсу в точках 5 и 2 (рис. 3.59). Эти касательные будут перпендикулярны диаметру 5— 2, а прямые, проведенные через точки А и В параллельно этим касательным, будут также перпендикулярны прямой 5— 2. Обозначьте точки, полученные на пересечении этих прямых с эллипсом, как 1, 3, 4, 6 (рис. 3.60). Соедините все шесть вершин прямыми линиями (рис. 3.61).
Проверьте правильность вашего построения разными способами. Если построение верно, то линии, соединяющие противоположные вершины шестиугольника, пересекаются в центре окружности (рис. 3.62), а противоположные стороны шестиугольника параллельны соответствующим диаметрам (рис. 3.63). Еще один способ проверки показан на рис. 3.64.
Вертикальный шестиугольник
В таком шестиугольнике прямые, соединяющие точки 1 и 3, 6 и 4, а также касательные к описанной окружности в точках 5 и 2, имеют вертикальное направление и сохраняют его на перспективном рисунке. Таким образом, проведя две вертикальные касательные к эллипсу, найдем точки 5 и 2 (точки касания). Соедините их прямой линией, а затем разделите полученный диаметр 5— 2 на 4 равных отрезка, учитывая их перспективные сокращения (рис. 3.65). Проведите вертикальные прямые через точки А и В, а на их пересечении с эллипсом найдите точки 7, 3, 6 и 4. Затем последовательно соедините точки 1— 6 прямыми (рис. 3.66). Правильность построения шестиугольника проверьте аналогично предыдущему примеру.
Описанный способ построения шестиугольника позволяет получить эту фигуру на основе окружности, изобразить которую в перспективе проще, чем
квадрат заданных пропорций. Поэтому данный способ построения шестиугольника представляется наиболее точным и универсальным. Способ постро
ения на основе квадрата позволяет легко изобразить шестигранник в том случае, когда на рисунке уже есть куб, иными словами, когда пропорции квадрата и направление его сторон определены.
На основе квадрата. Рассмотрите рис. 3.67. Вписанный в квадрат шестиугольник по горизонтальному направлению 5— 2 равен стороне квадрата, а по вертикали — меньше ее длины.
Вертикальный шестиугольник
Нарисуйте вертикальный квадрат в перспективе. Проведите через пересечение диагоналей прямую, параллельную его горизонтальным сторонам. Разделите полученный отрезок 5— 2 на четыре равные части и проведите через точки А и В вертикальные прямые (рис. 3.68).
Линии, ограничивающие шестиугольник сверху и снизу, не совпадают со сторонами квадрата. Изобразите их на некотором расстоянии (1/14 а) от горизонтальных сторон квадрата и параллельно им. Соединив найденные таким образом точки 1 и 3 с точкой 2, а точки 6 и 4 — с точкой 5, получим шестиугольник (рис. 3.69).
Гэризонтальный шестиугольник строится в той же последовательности (рис. 3.70 и 3.71).
Этот способ построения уместен только для шестиугольников с достаточным раскрытием. В случае, если раскрытие шестиугольника незначительно, лучше воспользоваться способом на основе описанной окружности. Для проверки шестиугольника, построенного через квадрат, можно использовать уже известные вам методы.
Кроме того существует еще один — описать вокруг полученного шестиугольника окружность (на вашем рисунке — эллипс). Все вершины шестиугольника должны принадлежать этому эллипсу.
Овладев навыками изображения шестиугольника, вы свободно перейдете к изображению шестигранной призмы. Внимательно рассмотрите схему
на рис. 3.72, а также схемы построения шестигранных призм на основе описанной окружности (рис. 3.73; 3.74 и 3.75) и на основе квадрата (рис. 3.76; 3.77 и 3.78).
Изобразите вертикальные и горизонтальные шестигранники различными способами. На рисунке вертикального шестигранника длинные стороны боковых граней будут параллельными друг другу вертикальными прямыми, а шестиугольник
основания будет тем больше раскрыт, чем дальше он находится от линии горизонта. На рисунке горизонтального шестигранника длинные стороны боковых граней будут сходиться в точке схода на горизонте, а раскрытие шестиугольника основания будет тем больше, чем дальше от зрителя он находится. Изображая шестигранник, следите также за тем, чтобы параллельные грани обоих оснований сходились в перспективе (рис. 3.79; 3.80).
Ghenadie Sontu Fine Art
BLOG
Рисование геометрических тел. Рисование призмы
Продолжая рассматривать принципы построения конструкции объемных тел, необходимо ознакомиться с изображением геометрических форм гранных предметов (трехгранная и шестигранная призмы).
Трехгранная призма характеризуется шестью точками пространственных углов оснований и тремя линиями ребер. Ось призмы определяется линиями, проведенными от пространственных углов оснований перпендикулярно к ее противоположным сторонам. Из точек их пересечения проводят вертикальную линию, которая и будет осью призмы. При построении трехгранной призмы необходимо правильно выбрать точку зрения. Предмет должен быть изображен таким образом, чтобы он выглядел трехмерным, с двумя видимыми плоскостями и передним ребром, несколько смещенным в сторону. Трехгранная призма при таком повороте будет наиболее выразительна, объемна и целесообразна при условии, что предмет расположен в оптимальном перспективном ракурсе.
Большие трудности испытывают студенты при определении величин отрезков граней в перспективном ракурсе на основании призмы. Чтобы избежать ошибок, рекомендуется использовать дополнительную окружность (в плане, вид сверху), на которой, в соответствии с видимым положением предмета, точно определяются пространственные углы основания призмы. Таким образом, для правильного изображения призматических форм необходимо построить цилиндрическую схему с последующим построением в ней гранных форм.
Построение трехгранной призмы следует начинать с проведения горизонтальной линии (она должна быть проведена строго горизонтально). Это дает возможность правильно определить положение поверхности оснований призмы по отношению к оси тела. После чего следует провести вертикальную осевую линию. Отмечая радиус основания, нарисовать окружность (эллипс) в перспективном ракурсе (рис.39). Для правильного определения пространственных точек углов основания на эллипсе необходимо над ним, в соответствии с радиусом эллипса, по одной оси нарисовать круг. Рисуя его, проверить, насколько правильно он нарисован, так как на искаженном круге невозможно будет точно определить пространственные точки и величины отрезков граней. От того, как верно они определены на круге, во многом будет зависеть правильность изображения поверхности основания призмы и всего предмета в целом.
Точно определив на круге видимое положение точек пространственных углов основания призмы, перенесите их на эллипс. Для определения ее верхнего, основания следует повторить рисунок эллипса, после чего, соединяя вертикальными линиями ребер пространственные точки оснований, получают построение изображения трехгранной призмы. На перспективном изображении призмы окружность (эллипс) нижнего основания должна быть несколько шире верхней.
Производя построение предмета на плоскости, следует строго соблюдать пропорции и перспективу. Для большей выразительности ее объемно-пространственной характеристики следует выделить ближние края формы более контрастными линиями, ослабляя и смягчая их по мере удаления. Во время продолжительного, многочасового занятия рисунком можно постепенно избавиться от всех вспомогательных линий. Рисунок в процессе построения следует выполнять легким нажимом карандаша на бумагу, с тем, чтобы по мере уточнения изображения можно было корректировать и удалять ненужное.
Шестигранная призма характеризуется двенадцатью точками пространственных углов основания и шестью линиями ребер. Ее ось определяется линиями, проведенными от противоположных пространственных углов основания, где точка их пересечения будет центром, через который проходит ось призмы. Для правильного определения ее пространственных углов, так же, как и при построении трехгранной призмы, необходимо начинать работу с построения эллипса и окружности под ним. В соответствии с видимым положением предмета при данной точке зрения следует правильно определить на окружности точки пространственных углов правильного шестигранника. Необходимо обратить внимание на поворот призмы, не следует рисовать шестигранную призму при симметричном расположении ее плоскостей. Поэтому при выборе места рисования нужно сесть так, чтобы предмет выглядел наиболее выразительно, объемно, как, например, показано на рис.40.
Перспективное построение шестигранной призмы производят тем же способом, как и при изображении трехгранной призмы. Сложность состоит в правильном определении с видимого положения перспективно сокращенных граней, их пропорциональных отношений. В этом случае также следует пользоваться вспомогательной окружностью в плане у нижнего основания призмы, как показано на рис.40. Построив окружность основания призмы, нужно определить шесть пространственных углов по окружности. При этом важно правильно отложить равные отрезки с учетом поворота призмы, т.е. с видимого положения. Соединяя точки легкими линиями, необходимо проследить за параллельностью противоположных сторон. Получив точки пространственных углов основания, так же, как и в первом случае, следует перенести их на нижнее основание эллипса. Необходимо отметить, что при переносе пространственных углов на основание эллипса учитывают перспективное сокращение его дальней половины, хотя эти изменения и несущественны. Главное, не допустить обратной перспективы.
Трехгранная пирамида (рис.41) характеризуется тремя точками пространственных углов основания, точкой вершины и шестью линиями ребер.
Для правильного изображения пирамиды рисунок следует начинать с построения ее основания, что аналогично построению призматической формы. Соединив точки пространственных углов основания линиями, необходимо найти конструктивную ось пирамиды и точку ее вершины.
Положение конструктивной оси определяется линиями, проведенными от пространственных углов основания перпендикулярно к его сторонам. От точки пересечения проводят вертикальную линию. Затем необходимо определить положение точки вершины пирамиды на осевой линии, что осуществляется в соответствии с пропорциональной величиной высоты натурной модели. После чего следует соединить вершину с пространственными углами основания.