Как начертить шестеренку в автокаде
Подпишитесь на автора
Подпишитесь на автора, если вам нравятся его публикации. Тогда вы будете получать уведомления о его новых статьях.
Отписаться от уведомлений вы всегда сможете в профиле автора.
Про моделирование и печать шестеренок здесь написано достаточно. Однако, большинство статей предполагают использование спец. программ. Но, у каждого пользователя есть своя «любимая» программа для моделирования. Кроме того, не все хотят устанавливать и изучать дополнительный софт. Как же моделировать профиль зуба шестерни в программе, где не предусмотрено вычерчивание эвольвентного профиля? Очень просто! Но муторно… 🙂
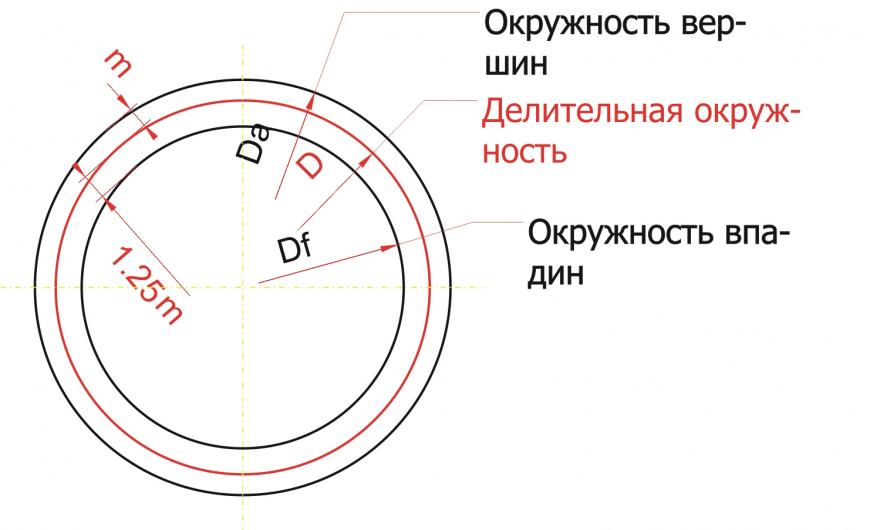
Определяем делительную окружность шестерни. Зачем это нужно? Чтобы определить межосевое расстояние. Т.е. где у вас будет располагаться одна шестерня, а где другая. Сложив диаметры делительных окружностей шестеренок и разделив сумму пополам, вы определите межосевое расстояние.
Чтобы определить диаметр делительной окружности нужно знать два параметра: модуль зуба и количество зубьев. Ну, с количеством зубьев – тут всем все понятно. Количеством зубьев на одной и другой шестерне определяется нужное нам передаточное отношение. Что такое модуль? Чтобы не связываться с числом «пи», инженеры придумали модуль. 🙂 Как вы знаете из курса школьной математики: D= 2 «Пи» R. Так вот, что касается шестеренок, там D = m* z, где D – это диаметр делительной окружности, m – модуль, z – количество зубьев. Модуль – величина, характеризующая размер зуба. Высота зуба равна 2,25 m. Модуль принято выбирать из стандартного ряда величин: 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16; 20; 25; 32 (ГОСТ-9563). Можно ли придумать «свой» модуль? Конечно! Но ваша шестеренка будет нестандартная! 😉
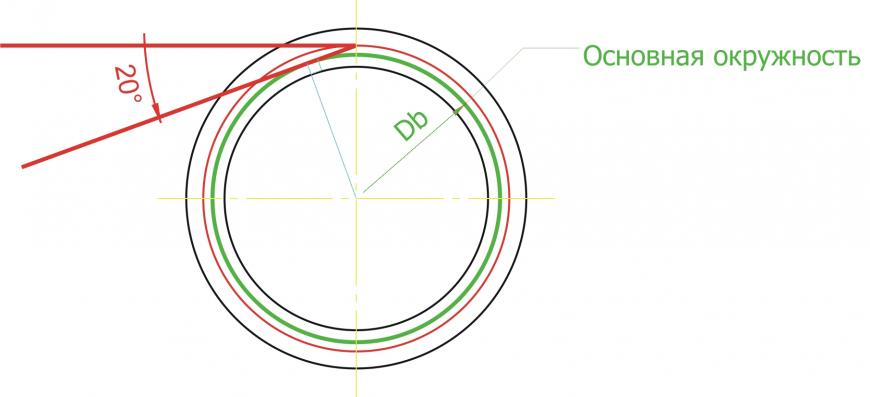
Строим основную окружность. Основная окружность – это окружность, по которой «перекатывается» прямая линия, своим концом вычерчивая эвольвенту. Формула для расчета диаметра основной окружности очень простая: Db = D * cos a, где а – угол рейки 20 градусов. Эта формула нам не нужна! Все гораздо проще. Строим прямую линию через любую точку делительной окружности. Удобнее взять самую высокую точку, на «12 часов». Тогда линия будет горизонтальная. Повернем эту линию на угол в 20 градусов против часовой стрелки. Можно ли повернуть на другой угол? Думаю, можно, но не нужно. 🙂 Кому интересно, ищем в литературе или интернете ответ на вопрос.
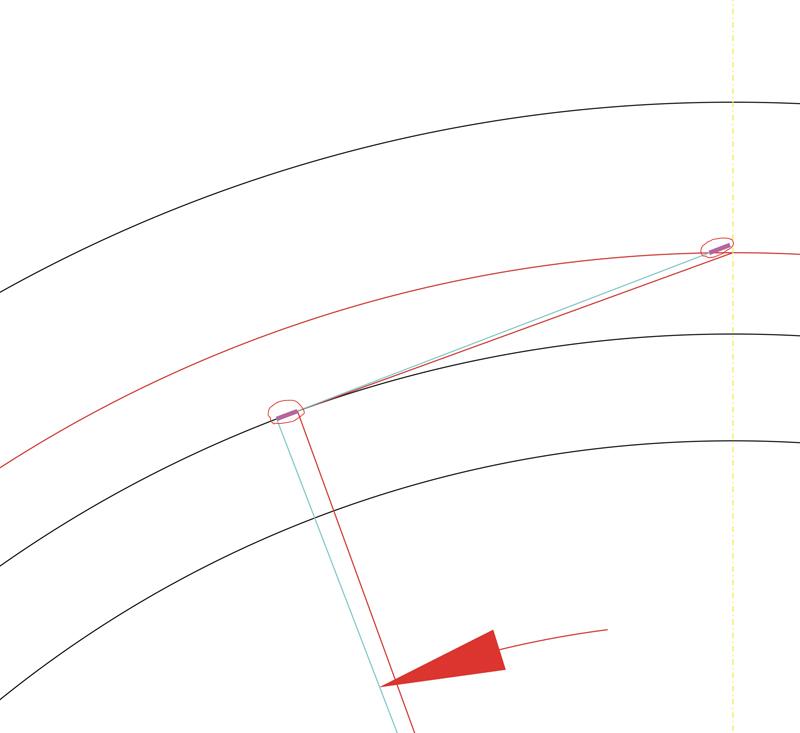
Прямую линию, которую мы получили, будем поворачивать вокруг центра шестерни маленькими угловыми шагами. Но, самое главное, при каждом повороте против часовой стрелки будем удлинять нашу линию на длину той дуги основной окружности, которую она прошла. А при повороте по часовой стрелки наша линия будет укорачиваться на ту же величину. Длину дуги или мерим в программе, или считаем по формуле: Длина дуги = (Пи * Db * угол поворота (в градусах)) / 360
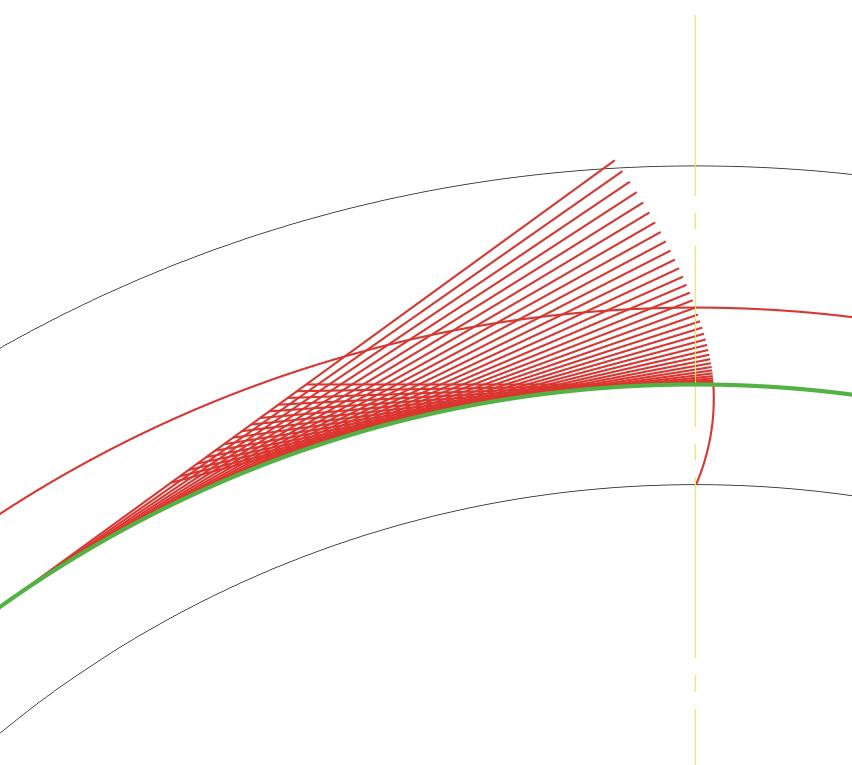
«Прокатываем» прямую линию по основной окружности с нужным угловым шагом. Получаем точки эвольвентного профиля. Чем точнее хотим строить эвольвенту, тем меньший угловой шаг выбираем.
К сожалению, в большинстве программ автоматического проектирования (CAD) не предусмотрено построение эвольвенты. Поэтому эвольвенту строим по точкам либо прямыми, либо дугами, либо сплайнами. При построении эвольвента заканчивается на основной окружности. Оставшуюся часть зуба до впадины можно построить дугой того же радиуса, который получается на трех последних точках. Для 3D печати я рисовал эвольвенту сплайнами. Для лазерной резки металла мне пришлось рисовать эвольвенту дугами. Для лазера нужно создать файл в формате dwg или dxf (для некоторых, почему-то, только dxf). «Понимает» лазер только прямые, дуги и окружности, сплайны не понимает. На лазере можно сделать только прямозубые шестерни.
Делим окружность на такое количество частей, которое в 4 раза больше количества зубьев шестерни. Эвольвенту отзеркаливаем относительно оси зуба и копируем с поворотом нужное количество раз.
Чтобы получить шестерню в объеме, то задаем толщину и получаем прямозубую цилиндрическую шестерню:
Если нужна косозубая шестерня, то вводим наклон зубьев и получаем:
Для получения шевронной шестерни, нужно отзеркалить косозубую шестерню относительно нужной торцевой поверхности:
Как смоделировать коническую шестерню, придумайте сами. 🙂
К вопросу о точности шестеренок. Те шестеренки, которые я распечатал на 3D принтере, сначала вращались, издавая легкое поскрипывание. Прошло некоторое время, и звук прекратился. Шестеренки «притерлись». 🙂
После модернизации принтера, шестеренки не печатал. Возможно, сейчас они напечатаются более точно, и не будут скрипеть.
Для вакуумной машины смоделировал пару – «шестерня-рейка». Их вырезали на лазере:
Подпишитесь на автора
Подпишитесь на автора, если вам нравятся его публикации. Тогда вы будете получать уведомления о его новых статьях.
Отписаться от уведомлений вы всегда сможете в профиле автора.