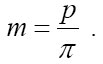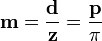Как начертить шестерню на бумаге

Подпишитесь на автора

Подпишитесь на автора, если вам нравятся его публикации. Тогда вы будете получать уведомления о его новых статьях.

Отписаться от уведомлений вы всегда сможете в профиле автора.

Про моделирование и печать шестеренок здесь написано достаточно. Однако, большинство статей предполагают использование спец. программ. Но, у каждого пользователя есть своя «любимая» программа для моделирования. Кроме того, не все хотят устанавливать и изучать дополнительный софт. Как же моделировать профиль зуба шестерни в программе, где не предусмотрено вычерчивание эвольвентного профиля? Очень просто! Но муторно… 🙂

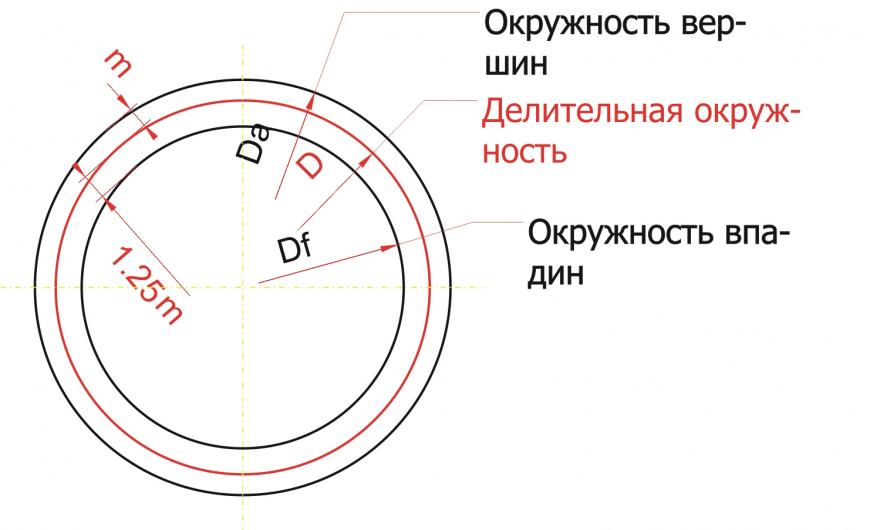
Определяем делительную окружность шестерни. Зачем это нужно? Чтобы определить межосевое расстояние. Т.е. где у вас будет располагаться одна шестерня, а где другая. Сложив диаметры делительных окружностей шестеренок и разделив сумму пополам, вы определите межосевое расстояние.

Чтобы определить диаметр делительной окружности нужно знать два параметра: модуль зуба и количество зубьев. Ну, с количеством зубьев – тут всем все понятно. Количеством зубьев на одной и другой шестерне определяется нужное нам передаточное отношение. Что такое модуль? Чтобы не связываться с числом «пи», инженеры придумали модуль. 🙂 Как вы знаете из курса школьной математики: D= 2 «Пи» R. Так вот, что касается шестеренок, там D = m* z, где D – это диаметр делительной окружности, m – модуль, z – количество зубьев. Модуль – величина, характеризующая размер зуба. Высота зуба равна 2,25 m. Модуль принято выбирать из стандартного ряда величин: 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16; 20; 25; 32 (ГОСТ-9563). Можно ли придумать «свой» модуль? Конечно! Но ваша шестеренка будет нестандартная! 😉

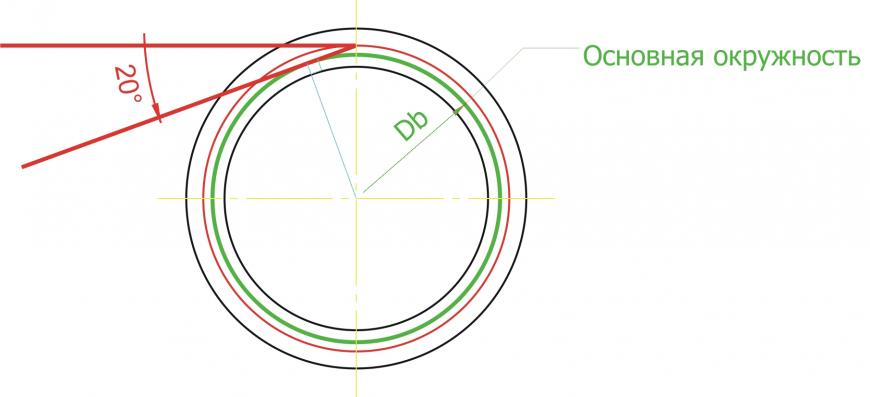
Строим основную окружность. Основная окружность – это окружность, по которой «перекатывается» прямая линия, своим концом вычерчивая эвольвенту. Формула для расчета диаметра основной окружности очень простая: Db = D * cos a, где а – угол рейки 20 градусов. Эта формула нам не нужна! Все гораздо проще. Строим прямую линию через любую точку делительной окружности. Удобнее взять самую высокую точку, на «12 часов». Тогда линия будет горизонтальная. Повернем эту линию на угол в 20 градусов против часовой стрелки. Можно ли повернуть на другой угол? Думаю, можно, но не нужно. 🙂 Кому интересно, ищем в литературе или интернете ответ на вопрос.

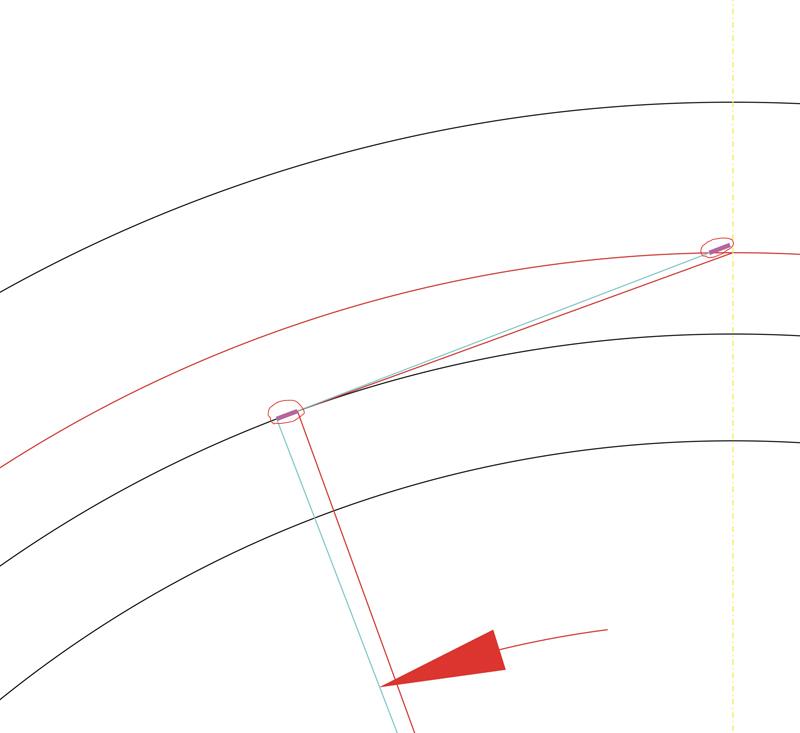
Прямую линию, которую мы получили, будем поворачивать вокруг центра шестерни маленькими угловыми шагами. Но, самое главное, при каждом повороте против часовой стрелки будем удлинять нашу линию на длину той дуги основной окружности, которую она прошла. А при повороте по часовой стрелки наша линия будет укорачиваться на ту же величину. Длину дуги или мерим в программе, или считаем по формуле: Длина дуги = (Пи * Db * угол поворота (в градусах)) / 360

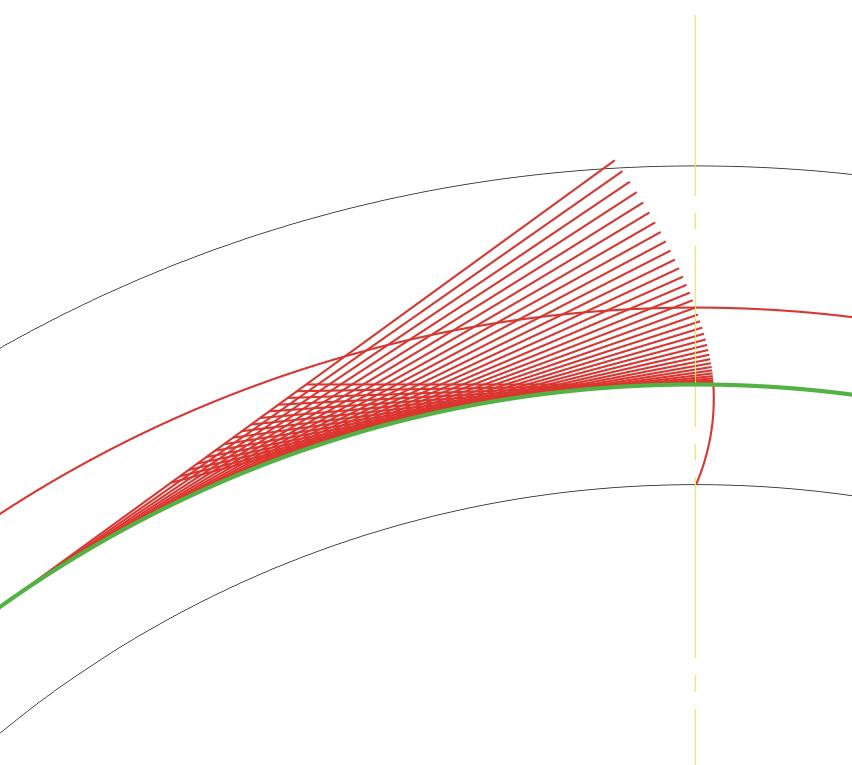
«Прокатываем» прямую линию по основной окружности с нужным угловым шагом. Получаем точки эвольвентного профиля. Чем точнее хотим строить эвольвенту, тем меньший угловой шаг выбираем.

К сожалению, в большинстве программ автоматического проектирования (CAD) не предусмотрено построение эвольвенты. Поэтому эвольвенту строим по точкам либо прямыми, либо дугами, либо сплайнами. При построении эвольвента заканчивается на основной окружности. Оставшуюся часть зуба до впадины можно построить дугой того же радиуса, который получается на трех последних точках. Для 3D печати я рисовал эвольвенту сплайнами. Для лазерной резки металла мне пришлось рисовать эвольвенту дугами. Для лазера нужно создать файл в формате dwg или dxf (для некоторых, почему-то, только dxf). «Понимает» лазер только прямые, дуги и окружности, сплайны не понимает. На лазере можно сделать только прямозубые шестерни.

Делим окружность на такое количество частей, которое в 4 раза больше количества зубьев шестерни. Эвольвенту отзеркаливаем относительно оси зуба и копируем с поворотом нужное количество раз.

Чтобы получить шестерню в объеме, то задаем толщину и получаем прямозубую цилиндрическую шестерню:

Если нужна косозубая шестерня, то вводим наклон зубьев и получаем:

Для получения шевронной шестерни, нужно отзеркалить косозубую шестерню относительно нужной торцевой поверхности:

Как смоделировать коническую шестерню, придумайте сами. 🙂

К вопросу о точности шестеренок. Те шестеренки, которые я распечатал на 3D принтере, сначала вращались, издавая легкое поскрипывание. Прошло некоторое время, и звук прекратился. Шестеренки «притерлись». 🙂

После модернизации принтера, шестеренки не печатал. Возможно, сейчас они напечатаются более точно, и не будут скрипеть.

Для вакуумной машины смоделировал пару – «шестерня-рейка». Их вырезали на лазере:

Подпишитесь на автора

Подпишитесь на автора, если вам нравятся его публикации. Тогда вы будете получать уведомления о его новых статьях.

Отписаться от уведомлений вы всегда сможете в профиле автора.

Источник

Уроки по SolidWorks

Урок посвящен построению зубчатого колеса с эвольвентным профилем зуба. Урок состоит из двух частей. В первой части выложена теория, формулы для расчета и один из способов графического построения эвольвентного профиля зуба.
Во второй части (видео) показан способ построения модели зубчатого колеса с использованием графических построений в первой части урока.

*Что такое эвольвента (эволюта)?
*Как построить эвольвенту?
*Как построить зубчатое колесо в программе SolidWorks?
*Формулы для расчета зубчатого колеса?
*Как нарисовать эвольвентный профиль зуба зубчатого колеса?

Итак, начнем с теории.

Параметры зубчатых колёс

Основной теореме зацепления удовлетворяют различные кривые, в том числе эвольвента и окружность, по которым чаще всего изготавливают профили зубьев зубчатого колеса.

В случае, если профиль зуба выполнен по эвольвенте, передача называется эвольвентной.

Для передачи больших усилий с помощью зубчатых механизмов используют зацепление Новикова, в котором профиль зуба выполнен по окружности.

Окружности, которые катятся в зацеплении без скольжения друг по другу, называются начальными (D).

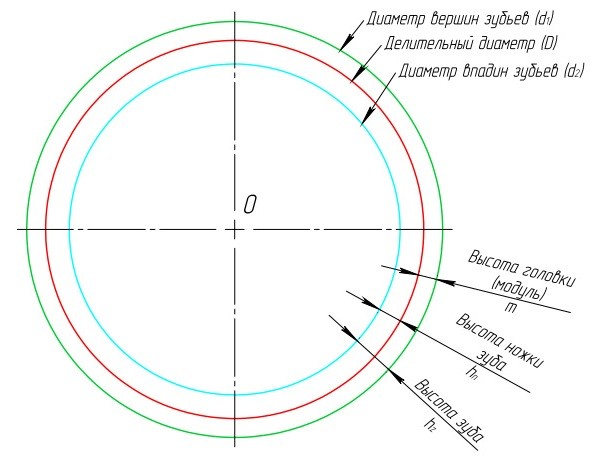
Окружности, огибающие головки зубьев зубчатых колёс, называются окружностями головок (d₁).

Окружности, огибающие ножки зубьев зубчатых колёс, называются окружностями ножек (d₂).

Окружности, по которым катятся прямые, образующие эвольвенты зубьев первого и второго колёс, называются основными окружностями.

Окружность, которая делит зуб на головку и ножку, называется делительной окружностью (D).

Для нулевых (некорригированных) колёс начальная и делительная окружности совпадают.

Расстояние между одноимёнными точками двух соседних профилей зубьев зубчатого колеса называется шагом по соответствующей окружности.

Шаг можно определить по любой из пяти окружностей. Чаще всего используют делительный шаг p =2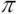r/z, где z – число зубьев зубчатого колеса. Чтобы уйти от иррациональности в расчётах параметров зубчатых колёс, в рассмотрение вводят модуль, измеряемый в миллиметрах, равный

Модуль зубчатого колеса, геометрический параметр зубчатых колёс. Для прямозубых цилиндрических зубчатых колёс модуль m равен отношению диаметра делительной окружности (D) к числу зубьев z или отношению шага p к числу «пи» .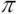

Модуль зубчатого колеса стандартизованы, что является основой для стандартизации других параметров зубчатых колёс.

Основные формулы для расчета эвольвентного зацепления:

Делительный диаметр рассчитывается по формуле:

Диаметр вершин зубьев рассчитывается по формуле:

d₁=D+2m

Диаметр впадин зубьев рассчитывается по формуле:

d₂=D-2*(c+m)

где с — радиальный зазор пары исходных контуров. Он определяется по формуле:

с = 0,25m

Диаметр основной окружности, развертка которой и будет составлять эвольвенту, определяется по формуле:

От автора. Я нашел в интернете полезную программку в Excel 2007. Это автоматизированная табличка для расчета всех параметров прямозубого зубчатого колеса.

Итак, приступим к графическому построению профиля зубчатого колеса.

Вот и готов профиль зуба прямозубого зубчатого колеса. В этом примере использовались следующие параметры:

На этом первая часть урока является завершенной. Во второй части (видео) мы рассмотрим как применить полученный профиль зуба для построения модели зубчатого колеса. Для полного ознакомления с данной темой («зубчатые колеса и зубчатые зацепления», а также «динамические сопряжения в SolidWorks») необходимо вместе с изучением этого урока изучать урок №24.

Еще скажу пару слов о специальной программе, производящей расчет зубчатых колес и генерацию модели зубчатого колеса для SolidWorks. Это программа Camnetics GearTrax.

P.S.(16.03.2010) Скачать Camnetics GearTrax

А теперь переходим с следующей части урока.

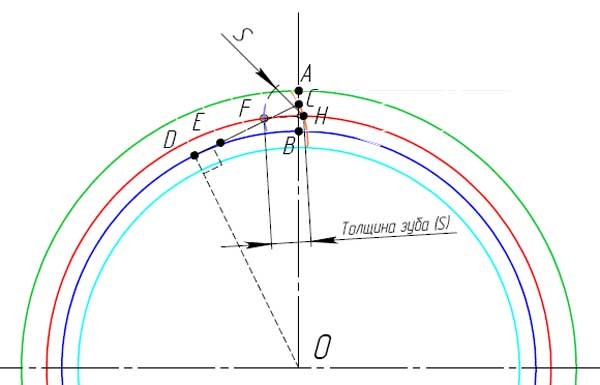
Толщина зуба по дуге делительной
окружности

s = Пи*m/2 = 1.57 m = 1.57 * 5 = 7.85

Я предыдущие удалю, чтобы не путать людей.

Даже колеса в библиотеке SolidWorks прорисованы упрощенно. При изготовлении
зубчатых колес (если Вы знаете) используется зуборезной инструмент (долбежка,
фрезеровка, шлифовка). Этот инструмент уже профилирован, тем более зубчатые шестерни
стандартизированы.

Высота головки нормальных зубчатых колес равна модулю.

Источник

Как изготовить шестерню по образцу своими руками

Одной из самых сложных и, тем не менее, распространенных механических систем является зубчатая передача. Это отличный способ передачи механической энергии из одного места в другое и способ увеличения или уменьшения мощности (крутящего момента), а также увеличения или уменьшения скорости чего-либо.

Как сделать шестеренку своими руками? Проблема всегда заключаются в том, что для создания эффективных зубчатых колес требуется достаточно много навыков рисования и знание математики, а также умение создавать сложные детали.

Для любительского нет необходимости иметь максимальную эффективность, поэтому мы можем получить намного более легкую в изготовлении систему, даже с подручными инструментами.

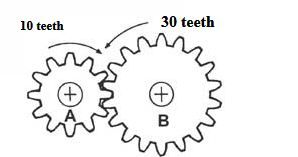
Шестерня — это ряд зубьев на колесе. (Обратите внимание на диаграмму выше, они пометили неправильное количество зубьев на шестернях — извините)

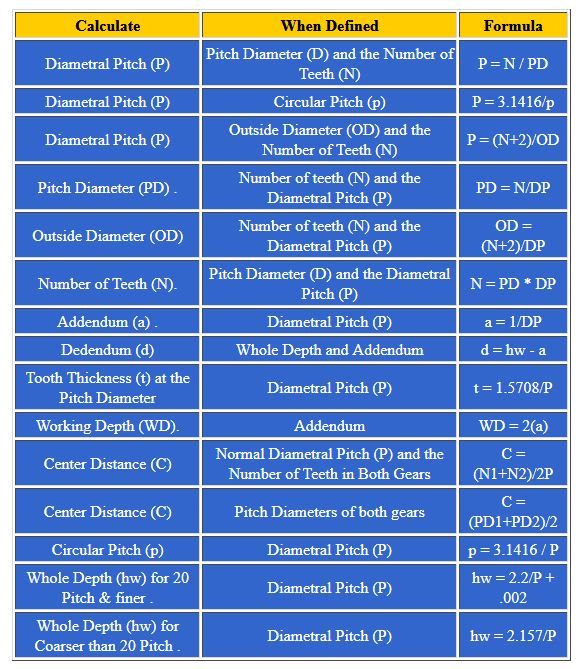
Шаг 1: Формулы и расчеты

Формулы для рисования и изготовления зубьев зубчатых колес в избытке можно найти в интернете, но для новичка они кажутся очень сложными.

Я решил упростить задачу, и решение очень хорошо работает как в больших, так и в малых масштабах. В небольших масштабах это лучше всего подходит для машинной резки с помощью лазерных резаков, например, очень маленькие зубчатые колеса могут быть успешно изготовлены таким образом.

Шаг 2: Простой способ

Итак, форма зубца, если говорить просто, может представлять собой полукруг.

Шаг 3: Определяем размеры

Теперь мы можем определить параметры, чтобы сделать шестерню:

Давайте начнем с зубьев размером 10 мм.

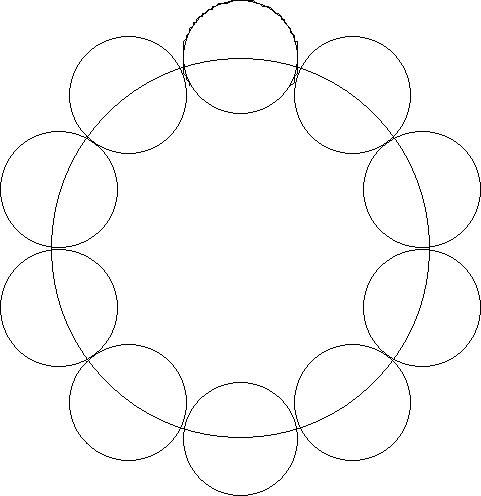
Я хочу шестерню с 5 зубьями, чтобы круг был 10х10 мм (в окружности) = 100 мм.

Чтобы нарисовать этот круг, мне нужно найти диаметр, поэтому я использую математику и калькулятор и делю окружность (100 мм) на Pi = 3,142.

Это дает мне диаметр 31,8 мм, и я могу нарисовать этот круг с помощью циркуля, а затем нарисовать с помощью циркуля на его окружности ровно 10 кругов диаметром 10 мм.

Если у вас есть такая возможность, то проще сделать все с помощью программного обеспечения для рисования. Если вы используете программное обеспечение, вы должны иметь возможность вращать круги зубьев вокруг основного круга, и вам нужно будет знать, как далеко повернуть каждый зуб. Это легко рассчитать: делите 360 градусов на количество кругов. Таким образом, для наших 10 кругов 360/10 = 36 градусов для каждого зуба.

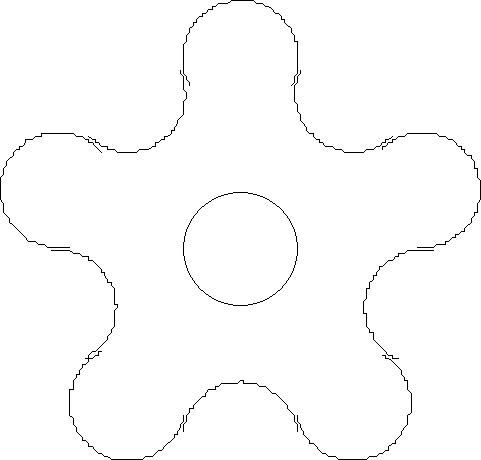
Шаг 4: Делаем зубчатую форму

Удалите верхнюю часть одного круга и нижнюю часть следующего круга. Чтобы сделать это, у вас должно быть четное количество зубьев

У нас есть первая шестерня. Она может быть вырезана из дерева или металла с помощью базовых подручных инструментов, пил и напильников.

Этот процесс легко повторить для любого количества шестеренок, которое вам нужно. Держите размер круга по образцу, и они будут соответствовать друг другу.

Шаг 5: Получите шестерёнку

Поскольку такие полукруглые шестеренки легко вырезать, вы можете сделать их с помощью подручного инструмента и лобзика или пилы.

Раньше я делал шаблон из 9 или 10 зубьев на фанере и использовал его в качестве ориентира для моего ручного фрезера и без проблем вырезал шестерни.

Если у вас есть доступ к лазерному резцу, они могут быть вырезаны из акрила 3 или 5 мм толщины и быть очень маленьких размеров.

Рассказываю как сделать какую-либо вещь с пошаговыми фото и видео инструкциями.

Источник

Чертежи зубчатого колеса

При создании технологического процесса производства и проведении других проектных работ зачастую создаются чертежи. Они отражают особенности геометрии изделия, а также его размеры и многие другие моменты. Чертежи зубчатого колеса или другого типа выполняются по упрощенной схеме с применением различных условных обозначений. Это связано с тем, что сложная форма изделия создает существенные трудности при ее полной детализации на момент создания чертежей. Оформить рассматриваемый документ с учетом всех требований достаточно сложно, для этого требуются определенные навыки и знания. Сегодня большинство чертежей создается в электронном виде при применении особых программ. Стоит учитывать, что они лишь частично упрощают процесс. Часто проектируется червячная зубчатая передача, чертежи которой можно встретить на самых различных сайтах.

Основные параметры зубчатого колеса

Создавать рассматриваемую конструкцию следует исключительно при заблаговременном создании чертежа, на котором отображаются основные параметры зубчатого колеса. Стоит отметить, что по создаваемой схеме некоторых механизмов также можно определить неправильный выбор основных параметров. В большинстве случае также делается упрощенный чертеж вала, за счет чего можно сразу определить принцип действия механизма.

Основными параметры, которые относятся к зубчатым колесам, являются:

Кроме этого, при создании технической документации уделяется внимание тому, в каких условиях происходит зацепление.

Если не учитывать основные параметры, то есть вероятность быстрого износа поверхности и появления многих других проблем.

Правила оформления чертежей

Довольно большое распространение получил чертеж цилиндрической зубчатой передачи. При его создании учитывается достаточно большое количество различных параметров. Правила выполнения рассматриваемой технической документации характеризуются следующими особенностями:

Следующий шаг заключается в создании вида слева. Госстандарт предусматривает наличие подобного вида, при создании самых различных технологических карт. Среди особенностей создания подобного вида отметим нижеприведенные моменты:

Таблица различных данных отображается в большинстве случаев справа в верхнем углу. Чтение подобной информации, как правило, не создает трудностей, так как она отображена числами.

Среди других особенностей отображения информации можно отметить следующие моменты:

В конструкторской документации ЕСКД указывается и некоторая другая информация, которая позволяет получить изделие с требуемыми параметрами. Примером можно назвать нанесение показателя шероховатости. Качественные изделия характеризуются довольно низким значение шероховатости, что достигается путем шлифования и полирования. Подобный показатель наносится на чертеж при помощи специальной полки.

Размер, ширина, габариты проставляются практически во всех случаях. Они позволяют сразу подобрать наиболее подходящую заготовку, в качестве которой часто применяется цилиндр. Не стоит забывать и про внутренний диаметр отверстия, которое предназначено для посадки на вал. Исключить вероятность прокручивания шестерни можно за счет создания шпоночного отверстия.

Чертеж, который применяется для изготовления пластмассового зубчатого колеса, несколько отличается от тех, по которым проводится производство стальных изделий. Это связано с эксплуатационными характеристиками изделия, особенностями применяемого материала при его изготовлении. Эскиз также изготавливается в соответствии со стандартами, в таблице указывается тип применяемого материала при изготовлении.

Довольно много внимания уделяется именно нанесению основных размеров. Часто встречается ситуация, когда из-за небольших размеров изделия или сложности отображаемого механизма нет достаточного количества свободного пространства. Инженер, которые занимается создание чертежа, должен предусмотреть правильное расположение всех размерных линий. Стоит учитывать, что определение размеров путем измерения линий на производстве не проводится, то есть все требуемые показатели для изготовления детали проставляются. В некоторых случаях проводится указание базовых размеров, от которых проводится вычисление других.

Довольно распространенным способом решения проблемы с большим количеством размерных линий можно назвать создание различных выносок.

Они существенно упрощают чтение информации.

При применении специальной программы для создания проектной документации следует учитывать, что в настройках указывается тип стрелок и многие другие моменты. В этом случае программ сама считает основные показатели между двумя указанными точками, за счет чего существенно упрощается поставленная задача.

В последнее время для создания чертежей зубчатых колес часто применяется программа автокад. Она встречается не только в бюро разработок, но и сборочном конвейере, так как позволяет открывать ранее созданные чертежи и проводить внесение различных изменений. Среди особенностей применения отметим следующие моменты:

На сегодняшний день в большинстве случаев применяются именно электронные чертежи. Это можно связать с простотой их использования, а также снижением вероятности допущения ошибок. Вся проектная документация должна создаваться исключительно с учетом масштаба. При применении рассматриваемой программы можно существенно повысить точность размеров.

В заключение отметим, что при работе в программе не стоит забывать о важности применения линий различной толщины и типа. Кроме этого, для их корректного отображения требуется более подходящее печатное оборудование, которое способно отображать линии различной толщины. В противном случае некоторые конструктивные элементы будет практически невозможно отобразить соответствующим образом.

Источник

1.2. Вычерчивание элементов зубчатого зацепления

Подсчитав все размеры элементов зацепления, приступаем к вычерчиванию зубчатого зацепления.

Размер в масштабе, мм

Пример расчета параметров зубчатого зацепления здесь.

Профили зубьев вычерчиваем в такой последовательности:

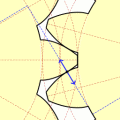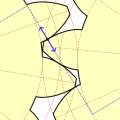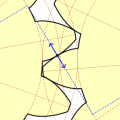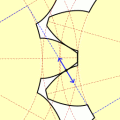
1. На чертеже под произвольным углом откладываем линию центров О₁О₂. Длина линии центров равна межосевому расстоянию О₁О₂=a_w.
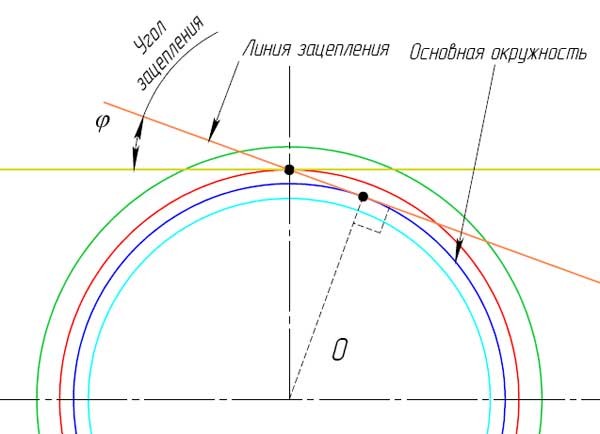
2. Из концов отрезка (линии центров) откладываем начальные окружности d_w1 и d_w2. Начальные окружности d_w1 и d_w2 касаются друг друга в полюсе P.
3. Откладываем и строим основные окружности d_в1 и d_в2.

4. Построение эвольвенты колеса 2.

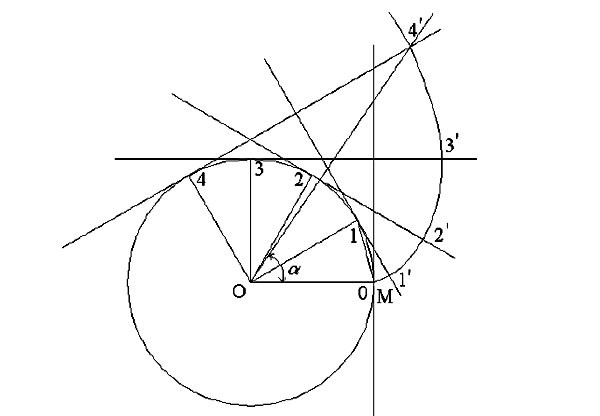
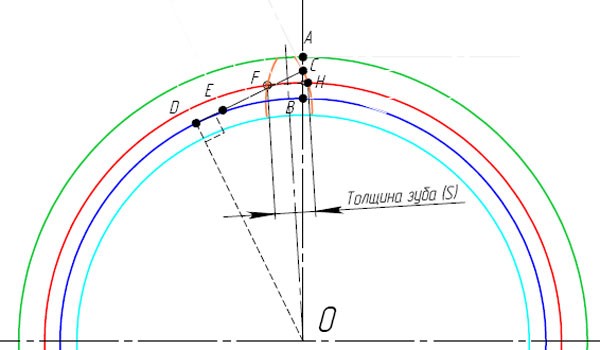
4.1. Из полюса P к основной окружности проводим касательную РА.
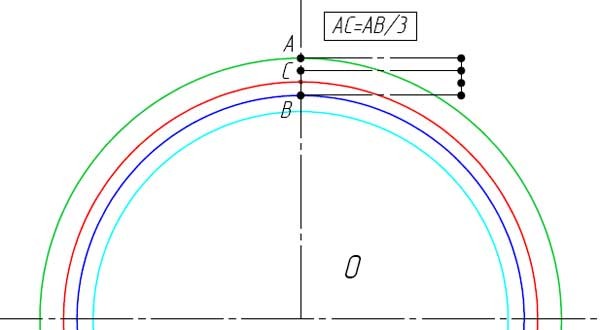
Отрезок АР (см. рис.) делим на четыре равные части (АВ = ВС = СD = DP) и из точки В проводим дугу радиуса r = ВР до пересечения в точке Р₁ с основной окружностью; тогда АР₁ = АР.

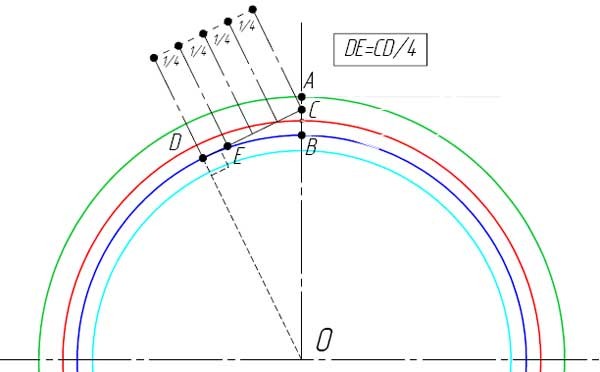
4.2. После этого, отрезок АР снова делим на произвольное число равных частей длиной 15…20мм (число делений целесообразно взять четным, например 8). Дугу АР₁ также делим на такое число равных частей (Р₁1’= 1′ 2′ = 2′ 3′ = …).

4.3. Точки 1′; 2′; 3’… соединяем с центром О₂.

4.4. Через точки 1′; 2′; 3’… проводим перпендикуляры к соответствующим радиусам О₂1′; О₂2′; О₂3’….
На перпендикулярах (они касаются основной окружности) откладываем отрезки 1’1»; 2’2»; 3’3»…, соответственно равные отрезкам Р1; Р2; Р3….

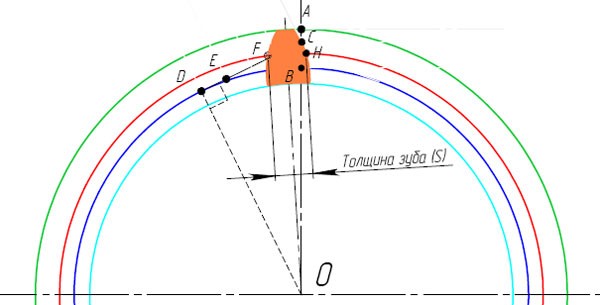
4.5. Соединяя точки Р₁; 1»; 2»; 3»… плавной кривой, получаем часть эвольвенты второго колеса.

4.6. Для продолжения построения профиля зуба второго колеса откладываем и строим окружности выступов и впадин зубьев второго колеса. Следует отметить, что радиус окружности впадин может быть больше, равен и меньше радиуса r_в основной окружности. Это зависит от числа Z зубьев колеса и от коэффициента смещения х. В нашем случае d_в2 > d_f2

4.6. Для завершения построения эвольвенты второго колеса вводим дополнительные точки 8 и 9. Точки 8 и 9 откладываем против часовой стрелки от точки А.
Пользуясь описанным выше методом, находим точки 8»и 9». Завершаем построение эвольвенты второго колеса.

4.7. Профиль ножки у основания зуба можно построить упрощенно. Если r_f

Источник