Как начертить треугольник в круге

Как начертить равносторонний треугольник

Из этого материала вы узнаете, как с помощью циркуля построить правильный треугольник. Напомним, что треугольник является правильным, если длина всех его сторон одинакова, а каждый из углов составляет 60°.

На листе бумаги отметьте произвольную точку. Установите в эту точку иглу циркуля и нарисуйте окружность.

Установите иглу циркуля в любую произвольную точку, лежащую на окружности, и нарисуйте вторую окружность с центром в этой точке.

При этом не меняйте раствор циркуля, то есть радиус первой окружности должен быть равен радиусу второй окружности.

Отметьте точки пересечения окружностей.

Соедините полученные точки линией. Полученный отрезок будет первой стороной треугольника.

Далее, через центры обеих окружностей нужно провести прямую линию.

Таким образом, у вас получилось три точки, которые будут тремя вершинами треугольника.

Соедините все три точки между собой.

Полученный треугольник имеет одинаковую длину сторон, а величина каждого его угла составляет 60°, а значит он правильный.

Источник

Как вписать треугольник в круг

Для любого треугольника всегда возможно построить описанную окружность, поскольку эта кривая однозначно определяется тремя заданными точками.

Чтобы это обнаружить, достаточно предположить, что треугольник задан декартовыми координатами своих вершин. В этом случае радиус и координаты центра окружности, проходящей через все три точки, должны быть решениями системы из трех уравнений второй степени с тремя неизвестными.

Эта система будет иметь единственное решение в том случае, если заданные точки не лежат на одной прямой (в этом последнем случае она вовсе не имеет решений). Но три точки, лежащие на одной прямой, не могут быть вершинами треугольника, следовательно, этот случай можно даже не рассматривать. Итак, решение заведомо существует.

Сторона вписанного треугольника будет являться хордой описанной окружности. Для любой такой хорды существует перпендикулярный к ней радиус, причем точка их пересечения делит хорду ровно пополам.

Следовательно, любой срединный перпендикуляр треугольника (то есть прямая, проходящая через середину его стороны и перпендикулярная ей) проходит через центр описанной окружности. Достаточно провести два таких перпендикуляра, и точка их пересечения будет центром. Радиус же описанной окружности однозначно определяется расстоянием до любой из вершин.

Источник

Треугольник вписанный в окружность

Определение

Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.

На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.

ВD = FC = AE — диаметры описанной около треугольника окружности.

O — центр вписанной в треугольник окружности.

Формулы

Радиус вписанной окружности в треугольник

r — радиус вписанной окружности.

Радиус описанной окружности около треугольника

R — радиус описанной окружности.

Площадь треугольника

S — площадь треугольника.

\[ S = \frac<1><2>ab \cdot \sin \angle C \]

Периметр треугольника

P — периметр треугольника.

Сторона треугольника

a — сторона треугольника.

Средняя линия треугольника

l — средняя линия треугольника.

Высота треугольника

h — высота треугольника.

\[ h = b \cdot \sin \alpha \]

Свойства

Доказательство

Около любого треугольника, можно
описать окружность притом только одну.

окружность и треугольник,
которые изображены на рисунке 2.

окружность описана
около треугольника.

окружность описана около треугольника,
что и требовалось доказать.

Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.

Источник

Как начертить треугольник в окружности?

Начертить при помощи циркуля окружность и выбрать на ней три любые точки. После чего при помощи линейки последовательно их соединить. Вот и все. В общем это очень легкое задание, если я его правильно понял

На самом деле с помощью циркуля есть смысл строить равносторонний треугольник. Любой треугольник можно построить пользуясь только линейкой. В данном случаи более интересно построить равносторонний треугольник. Итак, наши действия

Если быть точнее, то подключаются не фазы, а нагрузки, обмотки трансформаторов и генераторов. В трехфазной линии электропередач при включении обмоток источника электроэнергии треугольником линейное напряжение равно фазному. При включении обмоток источника электроэнергии звездой линейное напряжение больше фазного примерно в 1,73 раза. Кроме того, при включении питающего трансформатора звездой нулевая точка его обмоток заземляется на подстанции, что важно с точки зрения схемных решений по обеспечению электробезопасности.

Медиаторы бывают разные по толщине, форме. Есть даже металлические. Есть фирменные и именные. На концертных выступлениях разных групп, в микрофонной стойке они встроены в рядок, чтобы играющий мог брать, если потеряет, или уронит, или вдруг медиатор лопнет. Что бывает нередко.

В домашних условиях легко изготовить медиатор из старой кредитной карты. А раньше, в дикой молодости, мы вырезали их из крышек для банок. Дешево и сердито))

В продаже на али, я видел специальный компостер, или степлер, или корректнее, такой дырокол, позволяющий сразу пробивать медиатор из карты. Очень удобно, я считаю.

Кто-то даже коллекционирует медиаторы, покупая их в разных музыкальных магазинах мира.

Если ваша лучшая подружка пристает к вашему избраннику, то вы уверены, что она вам подружка, тем более лучшая? А делать ничего наверное не стоит,ну желательно конечно отдалить «подружку» от вашего дома и от вас, просто потому что это дружбой ну никак нельзя назвать. Если ваш избранник никак на это не реагирует, то замечательно, если реагирует, задам тот же вопрос, а вы уверенны, что он ваш избранник?

Источник

Построение с помощью циркуля и линейки – древнейший способ расчета в евклидовой геометрии. Известен со времен Древней Греции. Данная тема изучается в средних и старших классах на уроках геометрии.

Рассмотрим все случаи построения на конкретных примерах.

Построение отрезка, равного данному

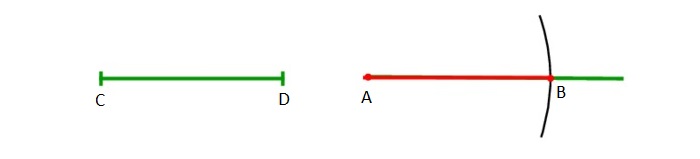
Строится луч, имеющий начало в т. A. Циркуль отмеряет существующий отрезок CD. Циркулем откладывается отрезок, равнозначный первому отрезку, на том же начерченном луче от его начала (A).

Для подобного чертежа ножку с иглой закрепляют в начале луча A, а с помощью части с грифелем проводится дуга до места соприкосновения с лучом. Данную точку можно обозначить т. B.

Отрезок AB будет равнозначен отрезку СD. Задача решена.

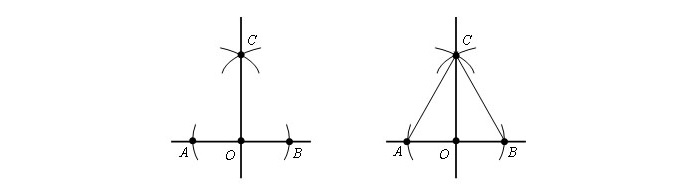
Деление отрезка пополам

Имеется отрезок AB.

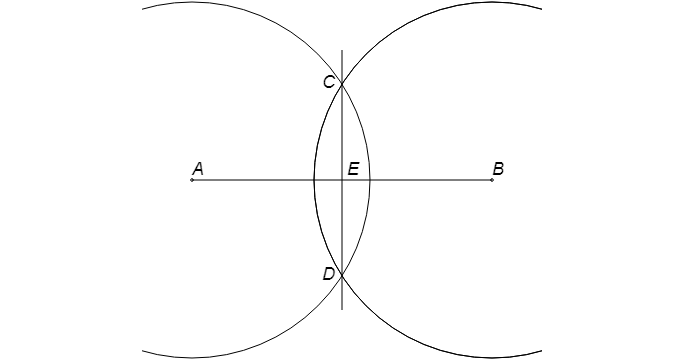
Сначала следует нарисовать окружность с радиусом больше половины отрезка AB с центром в т. A.

Далее чертится круг с тем же радиусом с серединой в т. B. В местах пересечения окружностей имеем т. C и т. D.

Сквозь эти точки требуется провести прямую линию. Получаем т. E, которая будет серединой отрезка AB.

Построение угла, равного данному

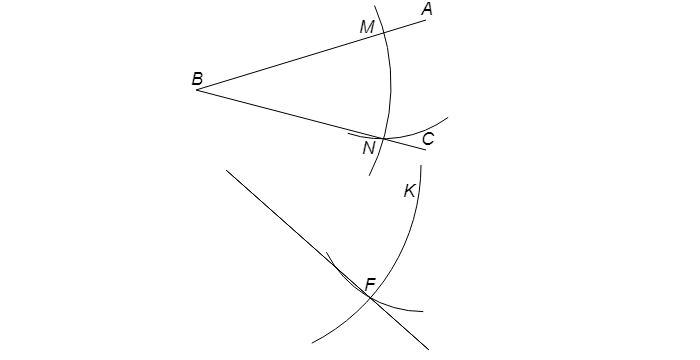
Вблизи угла проводится луч ED. Далее чертится окружность с серединой в т. B. В итоге имеем точки M и N.

Оставив раствор циркуля прежним, рисуют круг с серединой в т. E. В точке соприкосновения имеем т. K.

Поменяв раствор циркуля на длину расстояния между т. M и т. N, нужно провести окружность с серединой в т. K. В итоге получается т. F. После чертится прямая из т. E через т. F. Образуется угол DEF, который будет равнозначен углу ABC. Задача решена.

Построение перпендикулярных прямых

Пример 1

Точка O находится на прямой a.

Есть прямая и точка, находящаяся на ней. Нанести линию, идущую через существующую точку и находящуюся под прямым углом к имеющейся прямой.

Шаг 1. Чертим круг с рандомным радиусом r с серединой в т. O. Окружность соприкасается с прямой в т. A и т. B.

Шаг 2. Из имеющихся точек строится круг с радиусом AB. Точки С и D являются точками соприкосновения окружностей.

Приложив линейку, чертят прямую, сквозь т. O и одну из т. C или т. D, к примеру отрезок OC.

Доказательство, что прямая OC лежит перпендикулярно a.

Пример 2

Точка O находится вне прямой а.

Нарисовать окружность с радиусом r из т. O. Она должна проходить сквозь прямую a. A и B — точки её соприкосновения с прямой.

Рисуем линию, соединяющая т. O и т. O1.

Доказательство выглядит следующим образом.

Две прямые ОО₁ и AB пересекаются в т. C. Согласно третьему признаку равенства всех треугольников AOB = BO₁A. Из данного вывода следует, что угол OAC = O₁AC. Одноименные треугольники также будут равны (согласно первому признаку равенства всех треугольников).

Исходя из этого, выводим, что угол OCA = O₁CA, а, учитывая смежность углов, приходим к пониманию, что они прямые. А это означает, что OC – перпендикулярный отрезок, опущенный из т. O на прямую a. Задача решена.

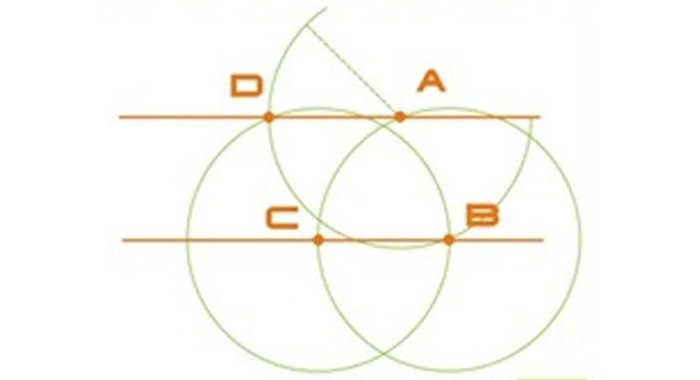
Построение параллельных (непересекающихся) прямых

Имеется прямая и т. А, не лежащая на этой прямой.

Нужно отметить прямую, проходящую через т. A, и параллельную имеющейся прямой.

Берется рандомная точка на имеющейся прямой и именуется B. С помощью циркуля строится окружность радиуса AB с серединой в т. B. В месте пересечения окружности и данной прямой отмечается т. C.

Оставив прежний радиус, рисуется еще одна окружность, теперь уже с центром в т. C. При правильных расчетах дуга должна пройти через т. B.

C тем же радиусом AB строится окружность с серединой в т. A. Точку соприкосновения второй и третьей окружностей назовем D. Третья окружность, учитывая верность расчетов, также пройдет через т. B.

Проводится прямая через т. A и т. D, которая станет параллельной первой. В итоге, получились две параллельные прямые, BC и AD.

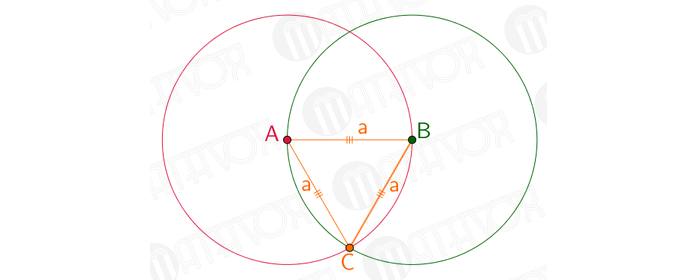
Построение правильного треугольника, вписанного в окружность

Правила построения правильного треугольника, вписанного в окружность:

Отметить отрезок AB, чья длина будет равняться а.

Взять циркуль. Часть с иголкой расположить на т. А, а часть с карандашом на т. B. Прочертить окружность. В итоге, радиус круга будет равнозначен длине отрезка AB.

Далее иглу размещают на т. B, а часть с грифелем на т. A. Чертится круг. В итоге, его радиус будет равнозначен длине отрезка AB.

На чертеже окружности пересеклись в двух точках. Далее нужно соединить т. A и т. B и одну из вышеупомянутых точек. В результате получится равносторонний треугольник.

Стороны такого треугольника равнозначны радиусам двух окружностей, которые равны длине а. Задача решена.

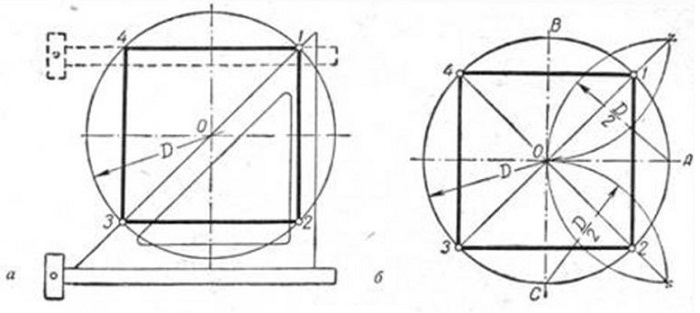
Построение правильного четырехугольника вписанного в окружность

Вариант 1

Исходя из данности, что диагонали любого квадрата пересекаются в середине окружности и находятся по отношению к его осям под углом 45 градусов, производят следующие действия. Пользуясь линейкой и уголком с углами 45 градусов (см. рисунок), размечают вершины т. 1 и т. 3.

Сквозь данные точки чертят отрезки, стороны четырехугольника, расположенные по горизонтали. Это т. 4 и т. 1, т. 3 и т. 2. В конце линейкой и уголком по его катету проводятся линии, расположенные по вертикали (высоты), отрезок т.1 — т. 2 и отрезок т. 4 — т. 3.

Вариант 2

Так как вершины правильного четырехугольника разделяют наполовину дуги окружностей, между точками диаметра (см. рисунок), то для достижения результата делают следующее: отмечают на точках перпендикулярных диаметров т. A, т. B и т. C и рисуют дуги до их соприкосновения.

После чертят прямые через места соприкосновения дуг, которые выделены на фигуре линиями. Точки соприкосновения с окружностью будут являться вершинами — это т. 1 и т. 3, т. 4 и т. 2. Данные вершины полученного квадрата соединяют друг с другом.

Задача выполнена двумя способами.

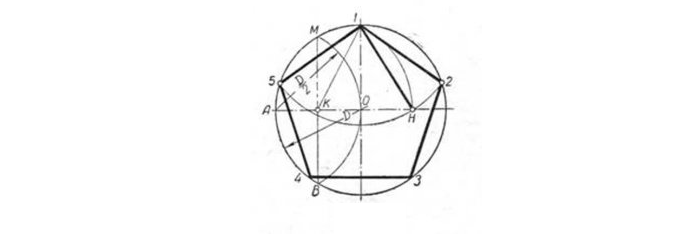
Построение вписанного в окружность правильного пятиугольника

Поместить на окружность т. 1, считая ее за вершину пятиугольника. Разделить отрезок AO пополам. Чтобы произвести подобную операцию, из т. A чертят дугу до места соприкосновения с окружностью в т. M и т. B.

Расположив конкретные точки на прямой, получаем т. K, и после совмещаем с т. 1. Радиусом, длина которого – отрезок А1, сделать изгиб из т. K до места соприкосновения с линией АО в т. H. После совместить т. 1 и т. H, образуя одну из пяти сторон пятиугольника.

Взять циркуль, величина раствора которого будет равна отрезку т.1 — т. H, нарисовать изгиб из т. 1 до соприкосновения с кругом. Так находят вершины 2 и 5. Отметив точки на вершинах 2 и 5, получают вершины 3 и 4. В конце все точки совмещают друг с другом.

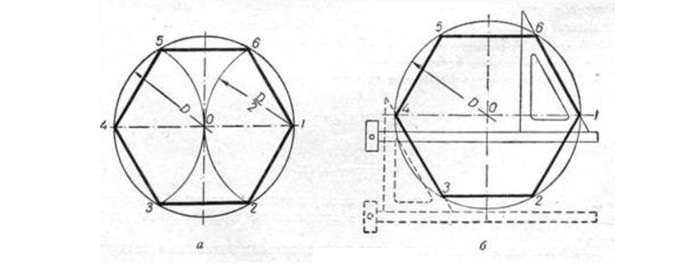
Построение правильного шестиугольника, вписанного в окружность

Решение подобной задачи строится на свойствах, где сторона шестиугольника равнозначна радиусу круга.

Для расчета разделяют круг на шесть ровных частей и последовательно совмещают все полученные точки (см. рисунок). Задача решена.

Источник