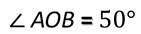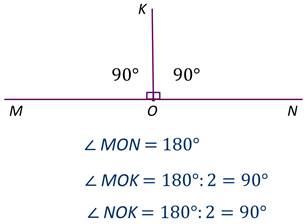Как начертить угол с минутами
Математика для блондинок
Страницы
воскресенье, 20 октября 2013 г.
Простое построение углов
Угол в тридцать градусов получается, когда по оси игрек мы возьмем половинку, а расстояние от центра системы координат до точки будет равно единице. При помощи циркуля и линейки такое построить можно, но.
 |
| Построение угла в 30 градусов |
Для подобного построения необходимо: построить декартову систему координат, нарисовать круг, по оси игрек разделить радиус пополам, через полученную точку провести линию, параллельную заданной. Фокус в том, что о декартовой системе координат древние люди не имели ни малейшего понятия. И ведь тысячелетиями как-то жили, и углы строили.
Теперь попробуем строить углы при помощи циркуля и линейки без всяких координатных систем. Проводим прямую линию, строим окружность с центром на построенной линии. Ставим циркуль в точки пересечения линии и окружности и строим две окружности того же радиуса. Соединяем линиями центр первой окружности точки пересечения окружностей. У нас получились углы в 60 градусов.
 |
| Построение угла в 60 градусов |
Почему возле углов я поставил циферки 1, 2, 3, 4, 5, 6? Я считаю, что именно такую единицу измерения углов использовали наши предки. Назовем эту единицу измерения углов «вавилонский угол». Дальше один угол делится на 60 градусов. Почему именно на 60? В те времена, в тех местах, использовалась шестидесятеричная система счисления. Вы такой системой счисления никогда не пользовались и понятия о ней не имеете? Ошибаетесь. Когда вы выражаете время в минутах и секундах, вы используете именно шестидесятеричное счисление. «Подожди пять минут» в переводе на десятичные дроби, если за единицу брать один час, будет звучать как «Подожди 0,083333333. часа». Дико звучит, не правда ли?
Давайте посмотрим на структуру вавилонских шестидесятеричных чисел. Единицу целого числа вавилоняне делили на шестьдесят частей. Потом каждую эту часть делили ещё на шестьдесят частей и так дальше. У шестидесятых долей были свои названия: минута, секунда, терция.
Но продолжим наши построения углов. Через центр первой окружности проводим перпендикуляр, затем строим ещё две окружности с центрами в точках пересечения перпендикуляра и первой окружности.
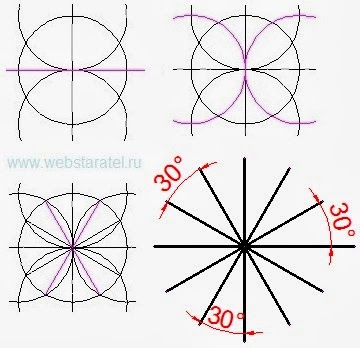 |
| Построение угла в 30 градусов |
Получился угол в 30 градусов. Как видите, построение очень простое, даже циркуль с переменным радиусом не нужен. Достаточно отрезать кусок разветвления ветки вместо циркуля и всё прекрасно получится. В этой первозданной простоте родились наши современные часы.
Как с помощью «жёлтого» угольника быстро размечать любые углы
На днях, знакомый профессиональный плотник показал мастерское применение угольника в качестве транспортира. Теперь я знаю, что обычным угольником можно построить не только углы 45° и 90°, а даже 10°, 20°, 30°, 40°, 50°, 60°, 70° и 80°.
Признаюсь, что перед написанием статьи я кучу времени уделил поиску этой темы в интернете — такого способа никто не предлагает, так что, эта статья является первоисточником.
Называется метод: «Правило одиннадцати».
Почему именно «одиннадцати»? В построении любого из углов, нам всегда требуется в первую очередь отложить 11 сантиметров. По данной технологии, угол будет строиться по прямоугольному треугольнику, а точнее — по двум его катетам, один из которых равен 11 см.
Самым первым делом, с помощью угольника — проводим перпендикуляр, удаленный от края заготовки на 11 см. На фото — перпендикуляр выделен красным цветом:
Теперь мы имеем отмеченный отрезок в 11 см. и перпендикуляр. Если любую точку этого перпендикуляра соединить с углом заготовки, то мы получим прямоугольный треугольник. А дальше, немного теории :-)))
Из школьного курса геометрии мы знаем, что именно отношение двух катетов прямоугольного треугольника и определяет тригонометрические функции угла (тангенса и котангенса)
Построение 20° и 70°
Смотрите! Откладывая 11 см. по горизонтали и 4 см. по вертикали мы получаем острый угол в 20°:
На фото, на построенном перпендикуляре отмечаю 4 см. и соединяю концы отрезков:
Измерение углов. Транспортир
Урок 43. Математика 5 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Измерение углов. Транспортир»
На этом уроке мы познакомимся с прибором для измерения углов – транспортиром. Научимся с помощью транспортира измерять и строить углы.
Коснёмся истории, чтобы узнать, как появился транспортир.
Понятие «градуса» и появление первых инструментов для измерения углов связывают с развитием цивилизации в древнем Вавилоне. Хотя само слово градус имеет латинское происхождение (градус – от лат. gradus – “шаг, ступень”). Предполагают, что создание транспортира было связано с созданием первого календаря.
Древние вавилонские математики и астрономы полный оборот (окружность) разделили на столько частей, сколько дней в году. Они думали, что в году 360 дней. Поэтому круг, обозначающий год, они разделили на 360 равных частей. Такое изображение было очень удобным. На нём можно было отмечать каждый прошедший день, и видеть, сколько дней осталось до конца года. Каждой части дали название – градус. Каждый градус разделили на 60 минут, а минуту – на 60 секунд. Градусная мера сохранилась и до наших дней.
Итак, для измерения углов применяют транспортир.
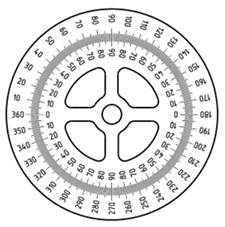
Транспортир состоит из линейки (прямолинейной шкалы) и полуокружности (угломерной шкалы). Центр этой полуокружности отмечен на транспортире или штрихом, или отверстием. Штрихи шкалы транспортира делят полуокружность на 180 долей. В некоторых моделях – на 360 долей – это круглые транспортиры.
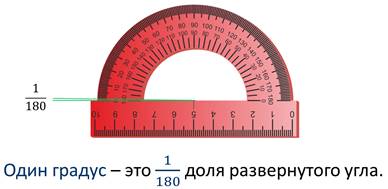
Если из центра этой полуокружности провести лучи через каждый штрих, то получится 180 углов. Каждый, из которых равен 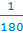
Такие углы принято называть градусами.
Градусы обозначают вот таким знаком °.
Каждое деление шкалы транспортира равно 1°. Кроме делений по 1° на шкале транспортира есть ещё деления по 5° и по 10°.
А теперь давайте разберёмся, как с помощью транспортира измерить угол. Запомните алгоритм измерения углов:
1) Совместить вершину угла с центром транспортира.
2) Расположить транспортир так, чтобы одна из сторон угла проходила через начало отсчёта на шкале транспортира; 0 – начало отсчёта.
3) Найдём штрих на шкале, через который пройдёт вторая сторона угла; (заметьте, используем ту шкалу для определения градусной меры угла, где располагается нулевой градус).
4) Смотрим, через какой штрих проходит вторая сторона и какой градус соответствует этому штриху.
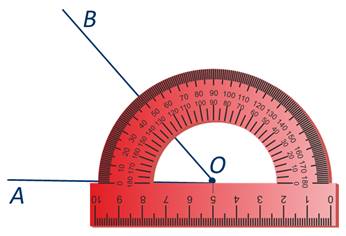
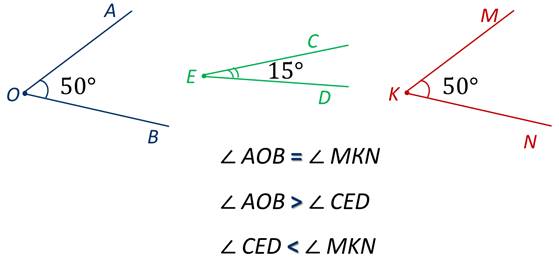
На нашем слайде угол АОВ равен 50°. Пишут так:
Развёрнутый угол равен 180°. Так как мы с вами выяснили, что прямой угол равен половине развёрнутого угла, то он равен
Прямой угол равен 90°.
Так как равные углы полностью совмещаются при наложении, то равные углы имеют равные градусные меры. Следовательно, больший угол имеет большую градусную меру, меньший угол имеет меньшую градусную меру.
Транспортир применяют и не только для измерения углов, а также и для их построения.
Запомним алгоритм построения углов.
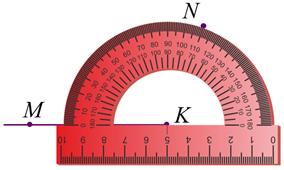
Алгоритм будем исследовать на конкретном примере: построить угол МКN равный 110°.
1. Отметим произвольную точку и обозначим её буквой К.
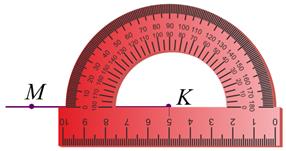
2. Начертим луч с началом в точке А и на нём отметим произвольную точку М. Получили луч КМ.
3. Наложим транспортир так, чтобы центр его совпал с точкой К, а луч КМ прошёл через начало отсчёта на шкале.
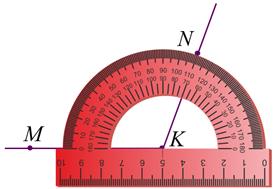
4. На этой же шкале транспортира найдём штрих, который соответствует 110°. Отметим на чертеже точку N против штриха с отметкой 110°.
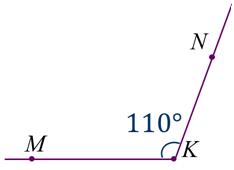
6. Не забудем записать
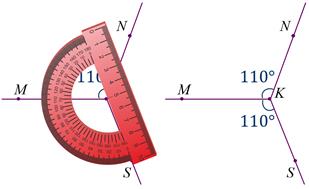
Такой же угол можно построить и по другую сторону от луча КМ.
Повсюду есть углы любые:
Прямые, острые, тупые,
Есть смежные, развёрнутые есть,
Их много, всех не перечесть.
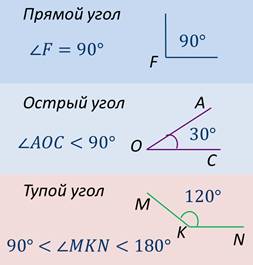
Если угол меньше 90°, то его называют острым углом.
Если угол больше 90°, но меньше 180°, то его называют тупым углом.
На экране изображены угол АОС – острый и угол МКN – тупой. Градусная мера угла АОС равна 30°, т.е. меньше 90°, следовательно, он острый. Градусная мера угла МКN равна 120°, т.е. больше 90°, но меньше 180°, следовательно, он тупой.
Итак, сегодня на уроке мы познакомились с прибором для измерения углов – транспортиром. Научились с помощью него измерять и строить углы.
Как начертить линию с заданным углом наклона?
А как Вы чертите вообще?
Используйте относительные координаты, то есть после запроса программы на указание следующей точки линии, в командной строке напечатайте: @(длина)
всё что связано с упорядоченным движением заряженных частиц
я ставлю первую точку затем пишу в диалоговом окне линии
Используйте относительные координаты, то есть после запроса программы на указание следующей точки линии, в командной строке напечатайте: @(длина)
я ставлю первую точку затем пишу в диалоговом окне линии

Таким же способом можно изменять и параметры уже построенного Отрезка и др. : активировать его крайнюю ручку ( она станет красной), переключением окон ТАБ выбрать корректируемый параметр и изменить.
Ну а общий случай построения отрезка под углом (второй его точки, когда первая указана мышью) в Автокаде с клавиатуры, конечно же:
Команда: _line Первая точка:
Следующая точка или [Отменить]: @150 *. И Случай, бог изобретатель. *
Как начертить линию с заданным углом наклона?
А как Вы чертите вообще?
Используйте относительные координаты, то есть после запроса программы на указание следующей точки линии, в командной строке напечатайте: @(длина)
всё что связано с упорядоченным движением заряженных частиц
я ставлю первую точку затем пишу в диалоговом окне линии
Используйте относительные координаты, то есть после запроса программы на указание следующей точки линии, в командной строке напечатайте: @(длина)
я ставлю первую точку затем пишу в диалоговом окне линии

Таким же способом можно изменять и параметры уже построенного Отрезка и др. : активировать его крайнюю ручку ( она станет красной), переключением окон ТАБ выбрать корректируемый параметр и изменить.
Ну а общий случай построения отрезка под углом (второй его точки, когда первая указана мышью) в Автокаде с клавиатуры, конечно же:
Команда: _line Первая точка:
Следующая точка или [Отменить]: @150 *. И Случай, бог изобретатель. *