Как начертить вписанную окружность в треугольник
Построение вписанной в треугольник окружности по точкам касания
По определению, вписанной в треугольник окружностью является окружность, касающаяся всех его сторон. Она наибольшая из тех, которые могут разместиться внутри треугольника. Центр этой окружности называется инцентром треугольника и расположен на пересечении его биссектрис. Перпендикуляры, восстановленные из сторон треугольника в точках касания вписанной окружности, тоже пересекаются в инцентре. На этом свойстве основан предлагаемый метод построения вписанной окружности.
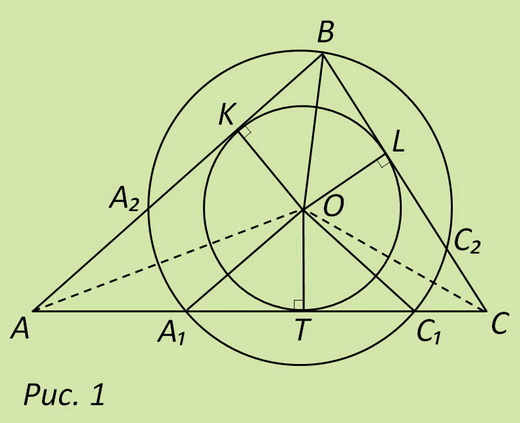
Второй вариант построения базируется на окружности, проведенной из инцентра треугольника через вершину одного из его углов, позволяющей определить местоположение точек касания вписанной окружности. Пусть в треугольник АВС (см. рис. 1) вписана окружность с центром О на пересечении биссектрис углов А и С. Соединим точки ее касания K, T и L сторон треугольника с инцентром. Согласно свойству касательной проведений к окружности, отрезки ОК, ОТ и ОL равны радиусу окружности и перпендикулярны сторонам треугольника.
Проведем дополнительно окружность из точки О радиусом ОВ т. е. проходящую через вершину наибольшего угла треугольника. Она отсекает три равные хорды А1С1, А2В и ВС2 на сторонах треугольника в виду концентричности вписанной окружности. Дополнительную окружность можно проводить через любую вершину треугольника. В этом случае придется продолжить его стороны (сторону), так как будем иметь дело с окружностью большего диаметра. Соединим инцентр треугольника с концами хорды А1С1. Прямоугольные треугольники А1ОТ и С1ОТ равны согласно тому, что гипотенузы А1О и С1О радиусы дополнительной окружности, а катет ОТ – общий. Следовательно точка Т середина, а ТО серединный перпендикуляр хорды А1С1. Аналогичным образом доказывается: ОК и ОL серединные перпендикуляры к двум другим хордам. Таким образом, середины хорд являются точками касания вписанной в треугольник окружности.
В треугольниках АОВ и АОС1 стороны ОВ и ОС1 радиусы дополнительной окружности, АО общая сторона и биссектриса угла ВАС. Тогда согласно равенству этих треугольников, отрезок АС†равен стороне АВ. В свою очередь отрезок А1С равен стороне ВС, ввиду сходного равенства треугольников А1ОС и ВОС.
Следствием вышеизложенного является возможность построения крайних точек хорды на стороне треугольника путем засечек дугами радиусами равными боковым сторонам из вершин прилежащих углов. Затем из вершины противолежащего стороне угла на одной из боковых стон откладывается длина второй хорды. Точка пересечения серединных перпендикуляров к полученным хордам – центр вписанной окружности.
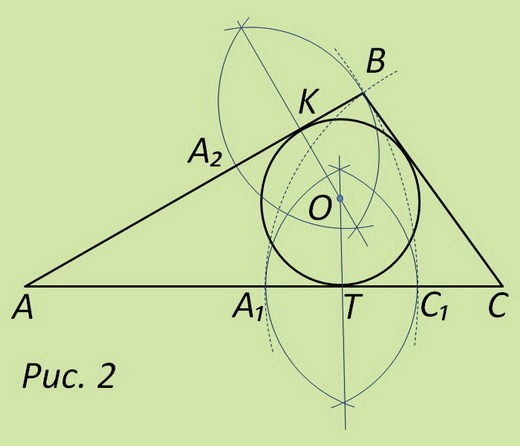
Построение в произвольно заданный треугольник АВС вписанной окружности изображено на рис. 2. На стороне АС (наибольшей, как на наиболее удобной) из вершины А дугой радиусом АВ делаем первую засечку в точке С1, а из вершины С дугой радиусом СВ – вторую в точке А1. К полученному отрезку А1С1 восстанавливаем серединный перпендикуляр. Раствором циркуля равным А1С1 из вершины В проводим дугу пересекающую например, сторону ВА в точке А2. Тем же раствором циркуля из точки А2 через вершину В опишем вторую дугу. Соединяем точки пересечения дуг прямой, получаем второй серединный перпендикуляр. Из точки пересечения перпендикуляров радиусом равным ОТ опишем искомую вписанную в треугольник окружность.
Определим количество линий примененных в данном построении. Пять на восстановление первого серединного перпендикуляра, три линии для второго и одну на проведение вписанной окружности. Всего девять. Если сравнивать два метода построения вписанной окружности по этому показателю – преимущество за последним.
Заключительный вывод: предлагаемое построение следует рассматривать в обучении наряду с общеизвестным методом.
13.04.2015 г. /Стрижак Василий Васильевич/ г. Речица, Гомельская обл.
Окружность, вписанная в треугольник. Теоремы и их рассмотрение

Формулировка теоремы об окружности, вписанной в треугольник выглядит следующим способом:
В треугольник можно вписать только одну окружность.
Формулировка теоремы о центре окружности, вписанной в треугольник, выглядит следующим образом:
Центральная точка окружности, вписанной в треугольник, есть точка пересечения биссектрис этого треугольника.
Окружность, вписанная в равнобедренный треугольник
Окружность считается вписанной в треугольник, если она хотя бы одной точкой касается всех его сторон.
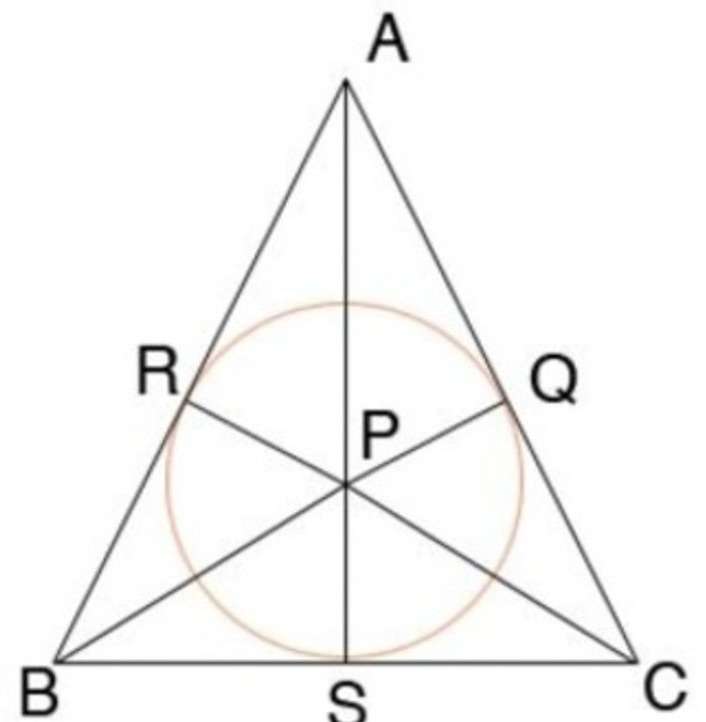
Одним из свойств равнобедренного треугольника является то, что вписанная окружность точкой касания делит основание пополам (BS = SC), а радиус вписанной окружности составляет треть высоты данного треугольника(SP=AS/3).
Свойства теоремы об окружности, вписанной в треугольник:
Окружность, вписанная в прямоугольный треугольник
Для треугольника с прямым углом действуют свойства теоремы об вписанной окружности в треугольник. И, кроме того, добавляется возможность решать задачи с постулатами теоремы Пифагора.
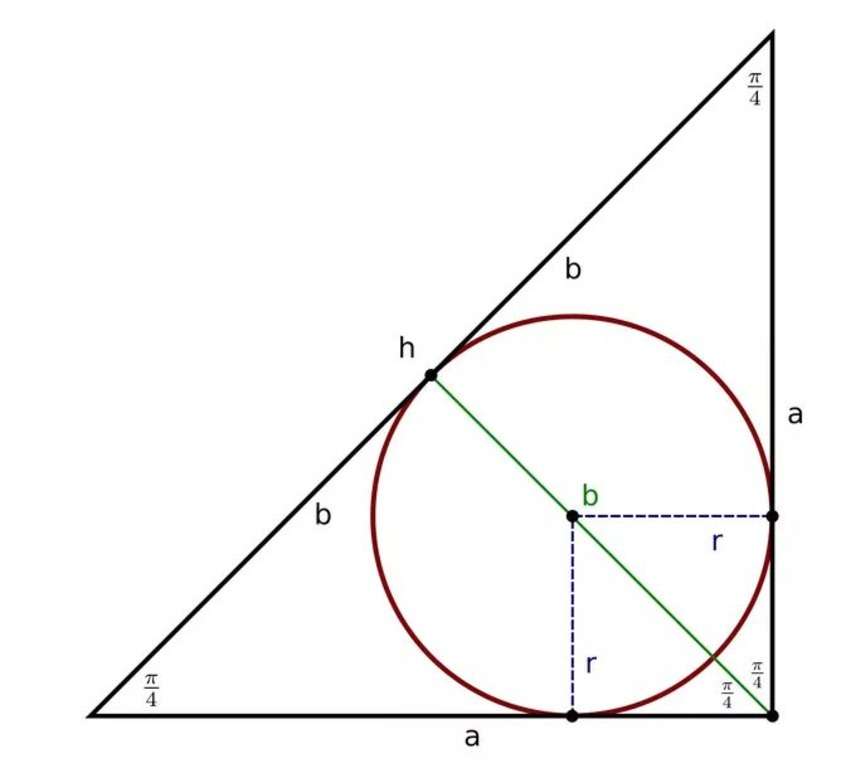
Радиус вписанной окружности в прямоугольный треугольник можно определить следующим образом: сложить длины катетов, вычесть значение гипотенузы и получившееся значение разделить на 2.
Формулировка теоремы о вписанной окружности
В планиметрии важны теоремы о вписанных и описанных фигурах. Одна из них звучит так:
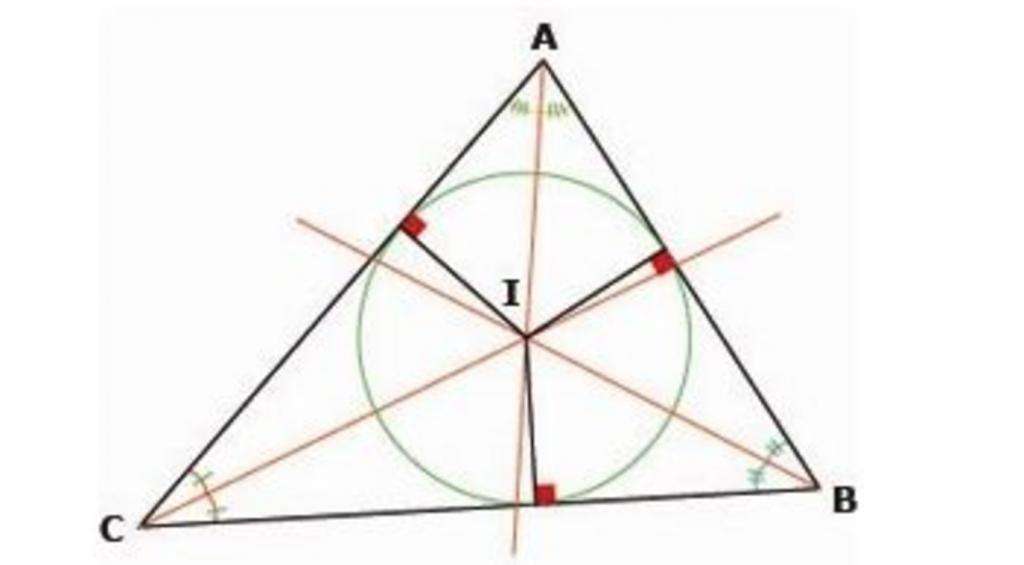
Центр окружности, вписанной в треугольник, является точкой пересечения биссектрис, проведенных из его углов.
На представленном рисунке показано доказательство данной теоремы. Показано равенство углов, и, соответственно, равенство прилегающих треугольников.
Теорема о центре окружности, вписанной в треугольник
Радиусы окружности, вписанной в треугольник, проведенные в точки касания перпендикулярны сторонам треугольника.
Задание «сформулируйте теорему об окружности вписанной в треугольник» не должно застать врасплох, потому что это одни из фундаментальных и простейших знаний в геометрии, которыми необходимо владеть в полной мере для решения многих практических задач в реальной жизни.
Окружность, вписанная в треугольник
Описание презентации по отдельным слайдам:
Окружность, вписанная в треугольник
Окружность называется вписанной в треугольник, если все стороны треугольника касаются окружности. A B C O
A B C D F E M N O K r r r Как вписать в окружность треугольник В треугольник можно вписать окружность, и притом только одну. Её центр – точка пересечения биссектрис треугольника. Проведём биссектрисы треугольника: АK, ВM, СN. Построим перпендикуляры ОD, OE, OF, которые равны между собой, т.к. равны соответствующие треугольники. Получаем ОD= OE= OF=r.
Задача №1 Построить вписанную окружность в: 1. остроугольный треугольник; 2. тупоугольный треугольник; 3. прямоугольный треугольник. Самостоятельная работа Построить вписанную окружность в: 1. остроугольный равнобедренный треугольник; 2. тупоугольный равнобедренный треугольник; 3. прямоугольный равнобедренный треугольник.
Положение центра вписанной окружности
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Номер материала: 278228
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В России утвердили новый порядок формирования федерального перечня учебников
Время чтения: 1 минута
Петербургский Политех перевел студентов на дистанционку
Время чтения: 1 минута
Московские школьники победили на международной олимпиаде по информатике
Время чтения: 1 минута
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Итоговое сочинение успешно написали более 97% выпускников школ
Время чтения: 2 минуты
В Минпросвещения рассказали о формате обучения школьников после праздников
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Треугольник вписанный в окружность
Определение
Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.
На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.
ВD = FC = AE — диаметры описанной около треугольника окружности.
O — центр вписанной в треугольник окружности.
Формулы
Радиус вписанной окружности в треугольник
r — радиус вписанной окружности.
Радиус описанной окружности около треугольника
R — радиус описанной окружности.
Площадь треугольника
S — площадь треугольника.
\[ S = \frac<1><2>ab \cdot \sin \angle C \]
Периметр треугольника
P — периметр треугольника.
Сторона треугольника
a — сторона треугольника.
Средняя линия треугольника
l — средняя линия треугольника.
Высота треугольника
h — высота треугольника.
\[ h = b \cdot \sin \alpha \]
Свойства
Доказательство
Около любого треугольника, можно
описать окружность притом только одну.
окружность и треугольник,
которые изображены на рисунке 2.
окружность описана
около треугольника.
окружность описана около треугольника,
что и требовалось доказать.
Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.
Как вписать треугольник в круг
Для любого треугольника всегда возможно построить описанную окружность, поскольку эта кривая однозначно определяется тремя заданными точками.
Чтобы это обнаружить, достаточно предположить, что треугольник задан декартовыми координатами своих вершин. В этом случае радиус и координаты центра окружности, проходящей через все три точки, должны быть решениями системы из трех уравнений второй степени с тремя неизвестными.
Эта система будет иметь единственное решение в том случае, если заданные точки не лежат на одной прямой (в этом последнем случае она вовсе не имеет решений). Но три точки, лежащие на одной прямой, не могут быть вершинами треугольника, следовательно, этот случай можно даже не рассматривать. Итак, решение заведомо существует.
Сторона вписанного треугольника будет являться хордой описанной окружности. Для любой такой хорды существует перпендикулярный к ней радиус, причем точка их пересечения делит хорду ровно пополам.
Следовательно, любой срединный перпендикуляр треугольника (то есть прямая, проходящая через середину его стороны и перпендикулярная ей) проходит через центр описанной окружности. Достаточно провести два таких перпендикуляра, и точка их пересечения будет центром. Радиус же описанной окружности однозначно определяется расстоянием до любой из вершин.