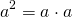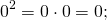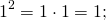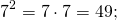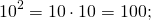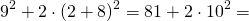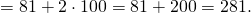Как находить числа в квадрате
Быстрое возведение чисел в квадрат без калькулятора
Сегодня мы научимся быстро без калькулятора возводить большие выражения в квадрат. Под большими я подразумеваю числа в пределах от десяти до ста. Большие выражения крайне редко встречаются в настоящих задачах, а значения меньше десяти вы и так умеете считать, потому что это обычная таблица умножения. Материал сегодняшнего урока будет полезен достаточно опытным ученикам, потому что начинающие ученики просто не оценят скорость и эффективность этого приема.
Для начала давайте разберемся вообще, о чем идет речь. Предлагаю для примера сделать возведение произвольного числового выражения, как мы обычно это делаем. Скажем, 34. Возводим его, умножив само на себя столбиком:
1156 — это и есть квадрат 34.
Проблему данного способа можно описать двумя пунктами:
1) он требует письменного оформления;
2) в процессе вычисления очень легко допустить ошибку.
Сегодня мы научимся быстрому умножению без калькулятора, устно и практически без ошибок.
Итак, приступим. Для работы нам потребуется формула квадрата суммы и разности. Давайте запишем их:
Например, 28 можно представить в следующем виде:
Аналогично представляем оставшиеся примеры:
Аналогично выбираем варианты и для остальных примеров:
Можете самостоятельно попробовать рассчитать оба разложения, и вы убедитесь, что разложение с наименьшим вторым слагаемым считается проще. А мы перейдем к примерам, которые посчитаем без калькулятора:
Вот так за три минуты мы сделали умножение восьми примеров. Это меньше 25 секунд на каждое выражение. В реальности после небольшой тренировки вы будете считать еще быстрее. На подсчет любого двухзначного выражения у вас будет уходить не более пяти-шести секунд.
Но и это еще не все. Для тех, кому показанный прием кажется недостаточно быстрым и недостаточно крутым, предлагаю еще более быстрый способ умножения, который однако работает не для всех заданий, а лишь для тех, которые на единицу отличаются от кратных 10. В нашем уроке таких значений четыре: 51, 21, 81 и 39.
Казалось бы, куда уж быстрее, мы и так считаем их буквально в пару строчек. Но, на самом деле, ускориться можно, и делается это следующим образом. Записываем значение, кратное десяти, которое наиболее близкое нужному. Например, возьмем 51. Поэтому для начала возведем пятьдесят:
Значения, кратные десяти, поддаются возведению в квадрат намного проще. А теперь к исходному выражению просто добавляем пятьдесят и 51. Ответ получится тот же самый:
И так со всеми числами, отличающимися на единицу.
Если значение, которое мы ищем, больше, чем то, которое мы считаем, то к полученному квадрату мы прибавляем числа. Если же искомое число меньше, как в случае с 39, то при выполнении действия, из квадрата нужно вычесть значение. Давайте потренируемся без использования калькулятора:
Как видите, во всех случаях ответы получаются одинаковыми. Более того, данный прием применим к любым смежным значениям. Например:
При этом нам совсем не нужно вспоминать выкладки квадратов суммы и разности и использовать калькулятор. Скорость работы выше всяких похвал. Поэтому запоминайте, тренируйтесь и используйте на практике.
Ключевые моменты
С помощью этого приема вы сможете легко делать умножение любых натуральных чисел в пределах от 10 до 100. Причем все расчеты выполняются устно, без калькулятора и даже без бумаги!
Для начала запомните квадраты значений, кратных 10:
Далее — выкладки квадрата суммы или разности, в зависимости от того, к какому опорному значению ближе наше искомое выражение. Например:
Как считать еще быстрее
Но это еще не все! С помощью данных выражений моментально можно сделать возведение в квадрат чисел, «смежных» с опорными. Например, мы знаем 152 (опорное значение), а надо найти 142 (смежное число, которое на единицу меньше опорного). Давайте запишем:
Обратите внимание: никакой мистики! Квадраты чисел, отличающиеся на 1, действительно получаются из умножения самих на себя опорных чисел, если вычесть или добавить два значения:
— это и есть формула.
— аналогичная формула для чисел, больших на 1.
Надеюсь, данный прием сэкономит вам время на всех ответственных контрольных и экзаменах по математике. А у меня на этом все. До встречи!
Квадрат числа
Что такое квадрат числа? Как найти квадрат числа?
Квадрат числа a — это произведение двух множителей, каждый из которых равен a.
Квадрат числа a обозначают a². Читают: «a в квадрате».
С помощью формулы определение квадрата числа a можно записать так:
Выражение a² назвали квадратом числа a, так как именно такой формулой выражается площадь квадрата со стороной a.
Таким образом, чтобы найти квадрат некоторого числа, надо это число взять множителем два раза и вычислить произведение.
Если числовое выражение содержит квадрат числа, значение квадрата вычисляют до выполнения остальных действий.
В математике находить квадраты чисел приходится достаточно часто. Для ускорения вычислений используется таблица квадратов.
Быстрое возведение чисел от 1 до 100 в квадрат
Вдохновленный этой статьей, решил поделиться с вами способом быстрого возведения в квадрат. Возведение в квадрат более редкая операция, нежели умножение чисел, но под нее существуют довольно интересные правила.

*квадраты до сотни
Для того, чтобы бездумно не возводить в квадрат по формуле все числа, нужно максимально упростить себе задачу следующими правилами.
Правило 1 (отсекает 10 чисел)
Для чисел, оканчивающихся на 0.
Если число заканчивается на 0, умножить его не сложнее, чем однозначное число. Стоит лишь дописать пару нулей.
В таблице отмечены красным.
Правило 2 (отсекает 10 чисел)
Для чисел, оканчивающихся на 5.
Чтобы возвести в квадрат двузначное число, оканчивающееся на 5, нужно умножить первую цифру (x) на (x+1) и дописать к результату “25”.
В таблице отмечены зеленым.
Правило 3 (отсекает 8 чисел)
Для чисел от 40 до 50.
Достаточно трудно, верно? Давайте разберем пример:
В таблице отмечены светло-оранжевым.
Правило 4 (отсекает 8 чисел)
Для чисел от 50 до 60.
Тоже достаточно трудно для восприятия. Давайте разберем пример:
В таблице отмечены темно-оранжевым.
Правило 5 (отсекает 8 чисел)
Для чисел от 90 до 100.
Похоже на правило 3, но с другими коэффициентами. Давайте разберем пример:
В таблице отмечены темно-темно-оранжевым.
Правило №6 (отсекает 32 числа)
Необходимо запомнить квадраты чисел до 40. Звучит дико и трудно, но на самом деле до 20 большинство людей знают квадраты. 25, 30, 35 и 40 поддаются формулам. И остается лишь 16 пар чисел. Их уже можно запомнить при помощи мнемоники (о которой я также хочу рассказать позднее) или любыми другими способами. Как таблицу умножения 🙂
В таблице отмечены синим.
Вы можете запомнить все правила, а можете запомнить выборочно, в любом случае все числа от 1 до 100 подчиняются двум формулам. Правила же помогут, не используя эти формулы, быстрее посчитать больше 70% вариантов. Вот эти две формулы:
Формулы (осталось 24 числа)
Для чисел от 25 до 50
Для чисел от 50 до 100
Конечно не стоит забывать про обычную формулу разложения квадрата суммы (частный случай бинома Ньютона):
UPDATE
Произведения чисел, близких к 100, и, в частности, их квадраты, также можно вычислять по принципу «недостатков до 100»: 
Словами: из первого числа вычитаем «недостаток» второго до сотни и приписываем двузначное произведение «недостатков».
Для квадратов, соответственно, еще проще.
Возведение в квадрат, возможно, не самая полезная в хозяйстве вещь. Не сразу вспомнишь случай, когда может понадобиться квадрат числа. Но умение быстро оперировать числами, применять подходящие правила под каждое из чисел отлично развивает память и «вычислительные способности» вашего мозга.
Кстати, думаю, все читатели хабры знают, что 64^2 = 4096, а 32^2 = 1024.
Многие квадраты чисел запоминаются на ассоциативном уровне. Например, я легко запомнил 88^2 = 7744, из-за одинаковых чисел. У каждого наверняка найдутся свои особенности.
Две уникальные формулы я впервые нашел в книге «13 steps to mentalism», которая мало связана с математикой. Дело в том, что раньше (возможно, и сейчас) уникальные вычислительные способности были одним из номеров в сценической магии: фокусник рассказывал байку о том, как он получил сверхспособности и в доказательство этого моментально возводит числа до сотни в квадрат. В книге так же указаны способы возведения в куб, способы вычитания корней и кубических корней.
Если тема быстрого счета интересна — буду писать еще.
Замечания об ошибках и правки прошу писать в лс, заранее спасибо.
Таблица квадратов натуральных чисел от 1 до 100
Таблица квадратов и таблица степеней.
Таблица квадратов представляет собой числа, которые возведены во вторую степень. Она используется для упрощения расчетов при возведении чисел во вторую степень.
Как пользоваться таблицей квадратов по схеме:
Чтобы возвести число в квадрат, нужно выбрать десятку и единицу числа, которое необходимо возвести во вторую степень, и на их пересечении будет число, которое получается за счет умножения этого числа на себя.
Например: рассмотрим на картинке ниже число 1849. Оно получилось за счет умножения числа 43 на 43 (43 во второй степени), в котором “4”- это десятка, а “3” – единица.
Или другой пример: число 4356 получилось за счет умножения числа 66 на 66 (66 во второй степени), в котором “6” сбоку – это десятка, а “6” сверху – единица.
Таблица квадратов:
Вторую степень называют “квадратом числа”. При этом умножение числа самого на себя происходит один раз (a · a).
Возведение в степень:
Возведение в степень – алгебраическое действие, при котором происходит умножение числа самого на себя столько раз, сколько указано в показателе.
Пример: 3 2 (три во второй степени) = 3 · 3 = 9, или
3 3 (три в третьей степени) = 3 · 3 · 3 = 27.
Таблица степеней:
Свойства степеней:
Произведение степеней. При умножении степеней с одинаковыми основаниями основание остаётся без изменений, а показатели степеней складываются.
6 2 · 6 4 = 6 2+4 = 6 6
Частное степеней. При делении степеней с одинаковыми основаниями основание остаётся без изменений, а из показателя степени делимого вычитают показатель степени делителя.
6 4 / 6 2 = 6 4 – 2 = 6 2
Возведение степени в степень. При возведении степени в степень основание степени остаётся без изменения, а показатели степеней перемножаются.
(6 4 ) 6 = 6 4 · 6 = 6 24
Степень произведения. При возведении в степень произведения каждый из множителей возводится в степень. Затем полученные результаты перемножаются.
Степень частного (дроби). Чтобы возвести в степень частное, можно возвести в эту степень отдельно делимое и делитель, и первый результат разделить на второй. При возведении в степень дроби нужно возвести в степень и числитель, и знаменатель.
Примечание: © Фото https://www.pexels.com, https://pixabay.com
Мировая экономика
Справочники
Востребованные технологии
Поиск технологий
О чём данный сайт?
Настоящий сайт посвящен авторским научным разработкам в области экономики и научной идее осуществления Второй индустриализации России.
Он включает в себя:
– экономику Второй индустриализации России,
– теорию, методологию и инструментарий инновационного развития – осуществления Второй индустриализации России,
– организационный механизм осуществления Второй индустриализации России,
– справочник прорывных технологий.
Мы не продаем товары, технологии и пр. производителей и изобретателей! Необходимо обращаться к ним напрямую!
Мы проводим переговоры с производителями и изобретателями отечественных прорывных технологий и даем рекомендации по их использованию.
О Второй индустриализации
Осуществление Второй индустриализации России базируется на качественно новой научной основе (теории, методологии и инструментарии), разработанной авторами сайта.
Конечным результатом Второй индустриализации России является повышение благосостояния каждого члена общества: рядового человека, предприятия и государства.
Вторая индустриализация России есть совокупность научно-технических и иных инновационных идей, проектов и разработок, имеющих возможность быть широко реализованными в практике хозяйственной деятельности в короткие сроки (3-5 лет), которые обеспечат качественно новое прогрессивное развитие общества в предстоящие 50-75 лет.
Та из стран, которая первой осуществит этот комплексный прорыв – Россия, станет лидером в мировом сообществе и останется недосягаемой для других стран на века.
Урок 25 Бесплатно Степень числа. Квадрат и куб числа
На данном уроке мы познакомимся с понятием степени числа.
Выясним, что называют «показателем степени» и «основанием степени».
Научимся вычислять квадрат и куб числа.
Составим таблицу степеней первых десяти натуральных чисел и рассмотрим ряд задач с использованием таких таблиц.
Определим, в каком порядке выполняют действия в выражениях, содержащих степень.
Степень числа
Известно, что сумму равных слагаемых можно заменить произведением.
Например, сумму пяти слагаемых, каждое из которых равняется четырем, можно записать короче:
4 + 4 + 4 + 4 + 4 = 5 ∙ 4
В произведении число 5 указывает на количество одинаковых слагаемых.
В свою очередь произведение одинаковых множителей тоже можно записать компактнее.
Произведение n одинаковых множителей можно представить в виде степени.
В буквенном виде произведение равных множителей можно представить следующим образом:
а— любое натуральное число.
Читают «а в n-ной степени» или «а в степени n».
Число а называют основанием (число, возводимое в степень).
n— это показатель степени (число, которое указывает сколько раз повторяется основание степени).
Степень числа представляют всегда так: записывают основание степени, а показатель ее записывают меньше размером в верхнем правом углу основания степени.
Операция умножения одинаковых множителей называется возведением в степень.
Например, произведение пяти множителей, каждое из которых равняется четырем, можно записать так:
4 ∙ 4 ∙ 4 ∙ 4 ∙ 4 = 4 5
Читают данную запись следующим образом:
4 5 — четыре в пятой степени.
Данная степень равна произведению трех двоек.
2— основание степени.
3— показатель степени.
Данная степень равна произведению четырех пятерок.
5— основание степени.
4— показатель степени.
Пройти тест и получить оценку можно после входа или регистрации
Квадрат и куб числа
Вторую степень числа называют квадратом числа.
Так, квадрат любого натурального числа а будет представлять собой произведение двух одинаковых множителей: а ∙ а = а 2 (говорят и читают «а в квадрате»).
2 2 (два во второй степени) иначе говорят и читают «два в квадрате».
10 2 (десять во второй степени) иначе говорят и читают «десять в квадрате».
27 2 (двадцать семь во второй степени) иначе говорят и читают «двадцать семь в квадрате».
Давайте сосчитаем квадраты первого десятка натуральных чисел (возведем во вторую степень первые десять натуральных чисел), используя таблицу умножения.
Один в квадрате равняется одному: 1 2 = 1 ∙ 1 = 1.
Два в квадрате равняется четырем: 2 2 = 2 ∙ 2 = 4.
Три в квадрате равняется девяти: 3 2 = 3 ∙ 3 = 9.
Четыре в квадрате равняется шестнадцати: 4 2 = 4 ∙ 4 = 16.
Пять в квадрате равняется двадцати пяти: 5 2 = 5 ∙ 5 = 25.
Шесть в квадрате равняется тридцати шести: 6 2 = 6 ∙ 6 = 36.
Семь в квадрате равняется сорока девяти: 7 2 = 7 ∙ 7 = 49.
Восемь в квадрате равняется шестидесяти четырем: 8 2 = 8 ∙ 8 = 64.
Девять в квадрате равняется восьмидесяти одному: 9 2 = 9 ∙ 9 = 81.
Десять в квадрате равняется сотне: 10 2 = 10 ∙ 10 = 100.
Оформим полученные данные квадратов натуральных чисел от 1 до 10 в виде таблицы.
Таблица квадратов первых десяти натуральных чисел
Учитывая данные таблицы квадратов, решим уравнение.
Решим уравнение х 2 = 49.
Решить уравнение- это значит найти корень уравнения (в нашем случае установить значение х).
Следовательно, корень уравнения (х) равен семи.
х 2 = 49
х = 7
Проверка: подставим найденное значение неизвестной (х = 7) в исходное уравнение х 2 = 49, получим:
7 2 = 49
7 ∙ 7 = 49
49 = 49
Ответ: х = 7.
У меня есть дополнительная информация к этой части урока!
Чтобы возвести в любую степень число 10, необходимо дописать после единицы нули, количество которых показывает показатель степени.
Разберем пример первый.
Найдите четвертую степень десяти (десять в четвертой степени 10 4 ).
10— это основание.
4— это показатель степени.
Так как по вышеизложенному правилу количество нулей после единицы должно быть равно показателю степени, то результат запишем следующим образом:
10 4 = 1 0000
На самом деле, если перемножить (по определению степени) четыре десятки, то получим:
10 4 = 1 0 ∙ 1 0 ∙ 1 0 ∙ 1 0 = 1 0000
Пример второй: найдите третью степень десяти (десять в третьей степени 10 3 ).
10— это основание.
3— это показатель степени.
Так как по правилу количество нулей после единицы должно быть равно показателю степени, то результат запишем следующим образом:
10 3 = 1 000
Соответственно, если перемножить (по определению степени) три десятки, то получим:
10 3 = 1 0 ∙ 1 0 ∙ 1 0 = 1 000
Рассмотрим обратную ситуацию:
Представим число 100 в виде степени с основанием 10.
Запишем основание 10, а показателем будет число, равное количеству нулей исходного числа (1 00 ).
Число 100 содержит два нуля, следовательно, это число в виде степени с основанием 10 представим следующим образом:
1 00 = 10 2
10— это основание.
2— это показатель степени.
Рассмотрим еще один подобный пример.
Представим число 10000 в виде степени с основанием 10.
Запишем основание 10, а показателем будет число, равное количеству нулей исходного числа (1 0000 ).
Данное число содержит четыре нуля, следовательно, 10000 в виде степени с основанием 10 представим следующим образом:
1 0000 = 10 4
10— это основание.
4— это показатель степени
Третья степень числа тоже имеет свое название.
Число в третьей степени называют кубом числа.
Так, куб любого натурального числа а будет представлять собой произведение трех одинаковых множителей: а ∙ а ∙ а = а 3 (говорят и читают «а в кубе»).
2 3 (два в третьей степени) иначе говорят и читают «два в кубе».
10 3 (десять в третьей степени) иначе говорят и читают «десять в кубе».
27 3 (двадцать семь в третьей степени) иначе говорят и читают «двадцать семь в кубе».
Давайте определим кубы первого десятка натуральных чисел (возведем в третью степень первые десять натуральных чисел), используя таблицу умножения.
Один в кубе: 1 3 = 1 ∙ 1 ∙ 1 = 1.
Два в кубе: 2 3 = 2 ∙ 2 ∙ 2 = 8.
Три в кубе: 3 3 = 3 ∙ 3 ∙ 3 = 27.
Четыре в кубе: 4 3 = 4 ∙ 4 ∙ 4 = 64.
Пять в кубе: 5 3 = 5 ∙ 5 ∙ 5 = 125.
Шесть в кубе: 6 3 = 6 ∙ 6 ∙ 6 = 216.
Семь в кубе: 7 3 = 7 ∙ 7 ∙ 7 = 343.
Восемь в кубе: 8 3 = 8 ∙ 8 ∙ 8 = 512.
Девять в кубе: 9 3 = 9 ∙ 9 ∙ 9 = 729.
Десять в кубе: 10 3 = 10 ∙ 10 ∙ 10 = 1000.
Оформим полученные данные кубов натуральных чисел от 1 до 10 в виде таблицы.
Таблица кубов первых десяти натуральных чисел
1000
С помощью таблицы кубов можно легко и просто решать примеры и задачи, в которых необходимо высчитывать третью степень числа.
Представим в виде куба число 343.
По таблице кубов видим, что 343 = 7 3
Проверим: найдем произведение трех семерок:
7 3 = 7 ∙ 7 ∙ 7 = 49 ∙ 7 = 343
На прошлом уроке мы подробно разобрали порядок выполнения арифметических действий в выражениях.
Выяснили, что в первую очередь выполняются арифметические действия в скобках, затем-действия второй ступени (умножение и деление) по порядку их следования слева направо, и только потом выполняются действия первой ступени (сложение и вычитание) по порядку слева направо.
Однако, в математических выражениях, в которых отсутствуют скобки, но есть действия первой, второй ступени и степень, возведение в степень выполняется раньше других действий, только потом умножают, делят, складывают и вычитают в установленном правилами порядке.
Если в скобках содержится степенное выражение, то действия в скобках выполняются по порядку слева направо, начиная с действий высшей ступени- возведение в степень, и далее по известным нам правилам.
За скобками действия выполняют, соблюдая порядок выполнения действий без скобок, рассмотренный выше.
Рассмотрим поясняющие примеры.
При решении различных задач и примеров будем пользоваться составленными таблицами степеней.
Пример 1.
Определим порядок действий в выражении и найдем его значение.
Так как исходное выражение не содержит скобки, а возведение в степень- это действие более высокой ступени, чем умножение, деление, сложение и вычитание, следовательно, в первую очередь необходимо выполнить вычисление степени, затем слева направо в порядке следования сначала действия второй ступени (деление), затем- действия первой ступени (вычитание).
1) 8 2 = 8 ∙ 8 = 64 (по определению степени или по таблице квадратов).
2) 64 ÷ 4 = 16
Пример 2.
Найдем значение данного выражения, определив порядок действий в нем.
Согласно порядка выполнения действий сначала выполняются действия в скобках.
Найдем разность 21 и 11.
Далее выполняется действие высшей ступени (возведение в степень), т.е. разность, полученную в скобках, возведем в квадрат.
Найдем, чему равно 10 2 по определению степени или по таблице квадратов.
2) 10 2 = 10 ∙ 10 = 100
Затем выполним действия, которые находятся в исходном выражении за скобками.
Определим третью степень двойки по таблице кубов или по определению степеней.
3) 2 3 = 2 ∙ 2 ∙ 2 = 8
4) 100 ∙ 8 = 800
У меня есть дополнительная информация к этой части урока!
С давних пор основными арифметическими операциями являются операции сложения, вычитания, умножения и деления.
Представление о степени, как об отдельной операции возникло не сразу.
Однако степени применялись при вычислении площадей и объемов уже у древних народов: степень числа высчитывали при решении различных задач в Древнем Египте, Древней Греции, в Вавилоне.
Диофант Александрийский древнегреческий математик, философ (III век н.э.) в своем знаменитом труде «Арифметика» описал первые натуральные степени чисел.
Диофант первым из античных ученых предложил специальные обозначения для шести степеней неизвестного (квадрат, куб, квадрато-квадраты, квадрато-кубы и т.д.)
Древнегреческий ученый Пифагор и его последователи (пифагорейцы) проявляли большой интерес к числам, искали в них скрытый смысл, закономерности и приписывали им различные свойства.
Пифагорейцы предполагали, что каждое число можно представить в виде фигуры.
Так, например, числа 4, 9, 16, 25 они представляли в виде квадратов.
В Древнем Вавилоне для вычисления и расчетов был создан целый ряд вычислительных таблиц: таблицы умножения, таблицы квадратов и кубов и многие другие.
В Древней Индии успешно развивалась наука.
Высоких результатов индийцы добились в астрономии, медицине, математике.
Индийские ученые часто оперировали большими числами.
В Древней Индии существовало понятие степени числа, математики того времени умели вычислять площади и объемы фигур, разработали алгоритмы вычисления всех арифметических операций, в том числе определение степени числа.
Важнейшим открытием индийских ученых в математике стало изобретение позиционной системы счисления, а также запись (чтение) чисел, для каждой цифры был придуман свой знак.
Математические труды их были изложены в основном в словесной форме на древнеиндийском языке в священных писаниях, книгах, сказаниях.
Потребность в решении более сложных математических задач со степенями заставляла ученых разных стран расширять понятие о степени, систематизировать и обобщать известные уже данные о ней.
В начале XV века самаркандский математик Гияс ад-Дин Джемшид Аль-Каши рассматривал нулевой показатель степени, в это же время французский ученый Никола Шюке применял в своих трудах нулевой и отрицательный показатель степени.
В 1544 г. немецкий математик Михаэль Штифель в своей книге «Полная арифметика» впервые ввел понятие «Показатель степени».
Постепенно понятие степени становится все шире, оно применяется не только к числу, но и к переменной.
Математики средневековья пытались установить единое обозначение степени и сделать ее компактней.
Французский ученый математик Франсуа Виет ввел буквенное обозначение (N, Q, C) для первой, второй и третьей степени.
Нидерландский математик Симон Стевин предложил называть степень по их показателям, отвергая тем самым словесные обозначения степеней, составленные Диофантом.
Современное обозначение степеней (а n ), где а-основание степени, n-показатель степени, ввел французский математик Рене Декарт.
Пройти тест и получить оценку можно после входа или регистрации