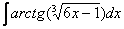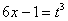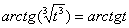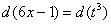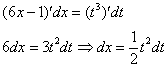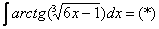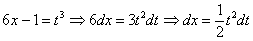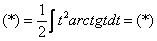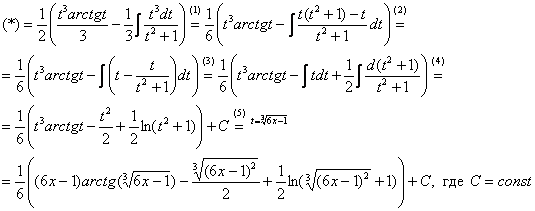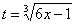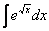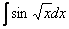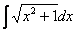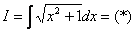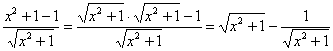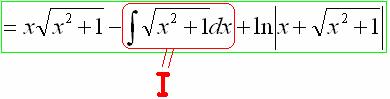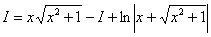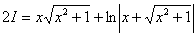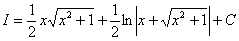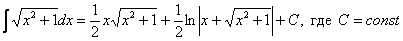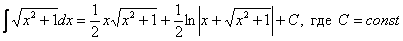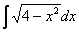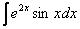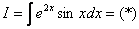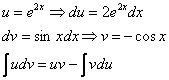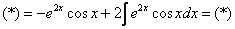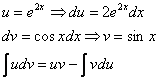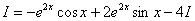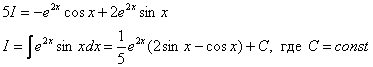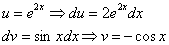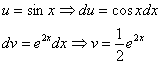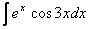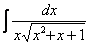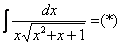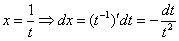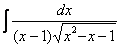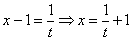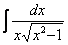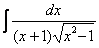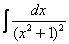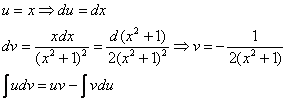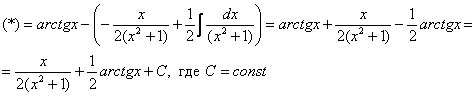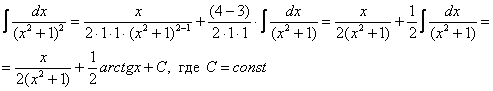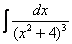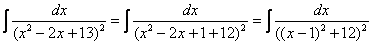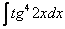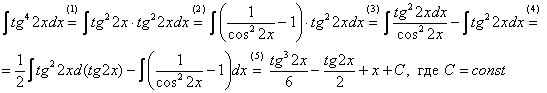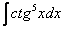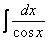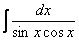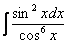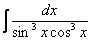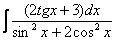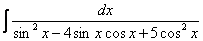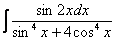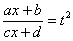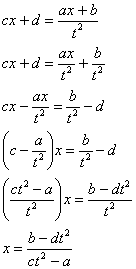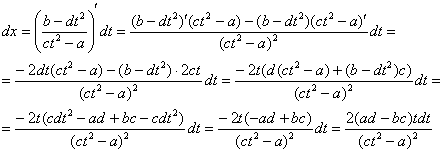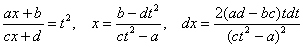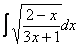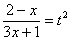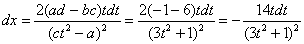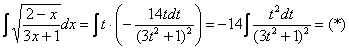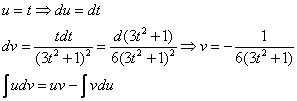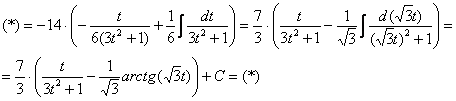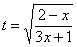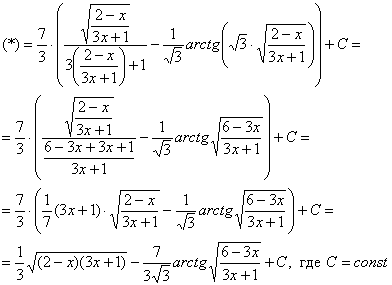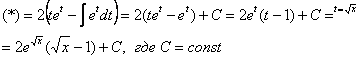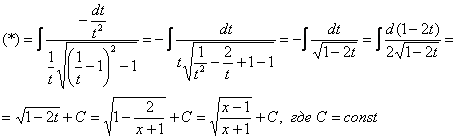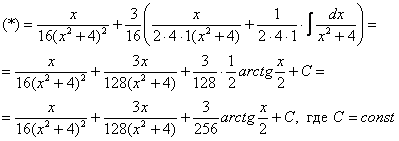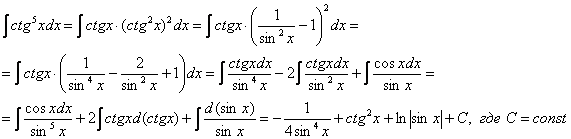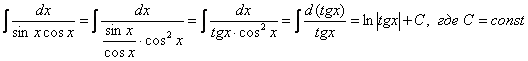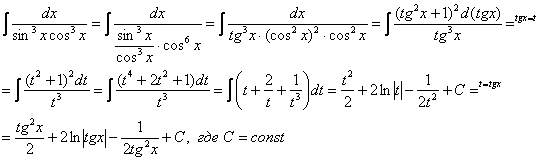Как находить интегралы сложных функций
Общая информация
В математике существуют функции, которые не поддаются интегрированию простыми методами. Некоторые алгоритмы также неприменимы в этом случае. Специалисты рекомендуют освоить нахождение первообразной на простых примерах. Этот принцип называется переходом от простого к сложному. Невозможно, не зная основ, переходить к решению сложных задач.
На начальных этапах обучения следует руководствоваться некоторыми правилами и алгоритмами. Их нужно освоить, и безошибочно решать простые задачи. Кроме того, следует разобраться в основном предназначении интеграла, и понять его геометрический смысл. Очень часто новички пытаются найти первообразную сложной функции. Некоторые пользуются информацией из интернета, которая бывает недостоверной. Но у них ничего не получается. Объяснение такому поражению — неверное обучение и отсутствие опыта.
Использование интеграла
Во многих дисциплинах применяется интеграл. Он обозначается литерой или символом «∫», и считается единицей дифференциального исчисления. Выражение (функция), которое идет после этого знака, называется подынтегральным. Его ограничением является знак дифференциала, т. е. «dx» или «dy». Под дифференциалом стоит переменная, по которой происходит поиск первообразной. Интегралом функции вида z = y (x) называется функция вида Y (x) с учетом константы «С» (Y (x) + C). Необходимо отметить, что Y (x) + C является первообразной функции y (x), которая была получена при дифференцировании.
Интегрирование очень часто применяется для нахождения площадей разнообразных фигур, когда невозможно воспользоваться какой-либо формулой. Например, площадь криволинейной трапеции следует искать толь при помощи операции интегрирования. Кроме того, при помощи данного метода выполняется нахождение объемов тел, пройденного пути при равноускоренном движении и т. д.
Следует отметить, что интегралы бывают двух типов: неопределенные и определенные. Вторые отличаются от первых конечным результатом, который является не первообразной, а некоторым численным значением. Если интеграл определенный, то необходимо воспользоваться формулой Ньютона — Лейбница, подставив в нее некоторые значения или границы. Она имеет такой вид с ограничениями a и b: F (y) = F (b) — F (a). Значение определенного интеграла соответствует разности первообразных, в которые подставляются верхняя и нижняя границы.
Интегралы бывают также собственными и несобственными. К первому типу относятся определенные интегралы, ограничениями которого являются область интегрирования и его подынтегральное выражение. Несобственный — интеграл определенного типа, который ограничен подынтегральным выражением или областью его интегрирования.
Геометрический смысл интеграла — площадь трапеции криволинейного типа. Стороной или сторонами фигуры являются кривые прямые. В этом случае найти площадь не удастся, поскольку формулы для этого не предусмотрены. Криволинейной называется плоская фигура, которая ограничена системой координат, неотрицательной функцией, а также прямыми. Значения ограничений нужно подставлять в формулу Ньютона — Лейбница. Фигура состоит из множества частей прямоугольной формы. При интегрировании их площади складываются, образуя общую площадь S.
Методика нахождения первообразной
Определение первообразной зависит от самой функции. Если она является элементарной, то для этого используется только простейший алгоритм, состоящий из двух шагов. Первым этапом является упрощение выражения, а вторым — определение исходной функции по таблице интегралов.
Некоторые выражения имеют свойство инвариантности, т. е. остаются неизменными при дифференцировании и интегрировании (экспонента в степени, которой является аргумент — e^x). В случае, когда подынтегральное выражение является сложным, то нужно применять специальный метод интегрирования по частям. Методика позволяет находить решения с высокой долей вероятности. Однако бывают функции очень сложные. При этом нужно применять метод замены, а затем правило интегрирования по частям.
Теорема имеет такую формулировку: первообразная сложной функции F (z, y) соответствует произведению ее составных элементов без интеграла, последнего элемента по первому. Следствие из нее — формула, позволяющая искать производную сложной функции. Пусть даны две непрерывные функции z = z (x) и y = y (x), имеющие производные. Соотношение необходимо рассматривать следующим образом: d (zy) = zdy + ydz. Нужно найти первообразные двух частей: ∫d (zy) = ∫(zdy + ydz). Произведение двух функций равно zy = ∫zdy + ∫ydz. Окончательная формула интегрирования по частям имеет такой вид: ∫zdy = zy — ∫ydz.
Формула применяется, когда невозможно найти первообразную какой-либо функции. Примером для интегрирования по частям является y = x * e^(2x). Однако не во всех случаях можно разобраться, когда стоит применять формулу. Ведь при неверном пути решения задания можно потерять много времени. Специалисты классифицировали функции, которые необходимо интегрировать по частям:
Необходимо также отметить, что в первом и во втором видах сложных функций, необязательно должно быть произведение. Оно может рассматриваться в виде дроби, умноженной на выражение.
Например, уравнение с натуральным логарифмом y = ln (x) / (x 2 — 4) можно записать в виде произведения (1 / (x 2 — 4)) * ln (x). Для нахождения первообразной умножения длинного натурального логарифма на переменную также нужно применять этот метод.
В некоторых случаях необходимо осуществлять замену выражения, которое находится под знаком интеграла, а затем, в зависимости от самой замены, находить значение по таблице первообразных или использоваться способ интегрирования по частям. Очень важно правильно определить алгоритм решения, поскольку он избавит от циклического разложения на множители и прочих операций.
Рекомендации специалистов
Для оптимизации нахождения первообразной или ее вычисления необходимо воспользоваться некоторыми советами математиков. Только правильное решение поможет успешно перейти от простых задач к сложным. К ним можно отнести следующие:
Следует отметить, что для нахождения первообразной применяется ручной и автоматизированный способы. Первый из них — решение задач самостоятельно, а второй — использование программного обеспечения. Специалисты рекомендуют универсальное онлайн web-приложение. Оно называется INTEGRAL CALCULATOR. Существует и офлайн-версия, которую поддерживают операционные системы Android, Windows, Mac и Linux. Кроме того, есть обыкновенный онлайн-калькулятор интегралов. Его следует использовать, когда нужно вычислять или находить первообразные.
Основное отличие онлайн от офлайн заключается в том, что в первом случае должно быть соединение с интернетом, а во втором — приложение устанавливается на жесткий диск. Оно позволяет находить первообразные, производные и т. д. При ручном методе решения следует руководствоваться подробным универсальным алгоритмом нахождения первообразной сложной функции по частям для неопределенного интеграла:
На третьем шаге алгоритма необходимо правильно определить параметры, поскольку это может существенно замедлить решение. Следует выбрать выражение, которое будет легко дифференцироваться и интегрироваться по частям. Например, в функции v = (x 2 ) * sin (2x) части следует выбирать таким образом: z = x 2 и y = sin (2x).
Специалисты рекомендуют выписать эти алгоритмы на отдельный лист, который должен быть постоянно в поле зрения. При регулярных тренировках надобность в «шпаргалке» отпадает. Если интеграл является собственным, то необходимо внимательно следить за решением, поскольку ограничением является также его подынтегральное выражение.
Примеры решения
Необходимо вычислить интеграл функции v = x * ln (x). Если границы не обозначены, то интеграл является неопределенным. Для этого следует воспользоваться универсальным алгоритмом нахождения первообразной по частям:
Нужно проинтегрировать функцию u = (x — 9) * e^(3x). Следует обратить внимание на выражение e^(3x), поскольку оно является сложным. Для решения рекомендуется применить также универсальный алгоритм:
Таким образом, интегрирование по частям следует применять в том случае, когда обыкновенные методы поиска первообразной не дают результата. Метод используется для понижения сложности подынтегрального выражения. Его можно применять неограниченное количество раз для одной функции.
Вычислить первообразную сложной функции
Вы будете перенаправлены на Автор24
Теоретическая часть
Понятие первообразной функции актуально в механике. Проблема нахождения функции по некоторой определённой производной этой же функции является задачей первообразной. Поэтому будем считать, что задачи по нахождению производных функций уже известны. Обычно понятие первообразной разбирают в рамках вопроса нахождения определённого интеграла.
Если известны основные элементарные производные, то задача нахождения первообразной разрешима.
Неопределённый интеграл от какой-либо функции представляет общий вид (выражение) всех её первообразных. Заметим, что первообразная и неопределённый интеграл существуют только для непрерывных функций на заданном промежутке.
Найти общее выражение первообразных представляется возможным, если решить неопределённый интеграл от заданной функции.
Практическая часть
Готовые работы на аналогичную тему
Рассмотрим примеры. Будем пользоваться таблицей неопределённых интегралов.
Рисунок 1. Таблица неопределённых интегралов. Автор24 — интернет-биржа студенческих работ
Рисунок 2. Пример. Автор24 — интернет-биржа студенческих работ
Рисунок 3. Пример. Автор24 — интернет-биржа студенческих работ
Рисунок 4. Пример. Автор24 — интернет-биржа студенческих работ
Рисунок 5. Пример. Автор24 — интернет-биржа студенческих работ
Рисунок 6. Пример. Автор24 — интернет-биржа студенческих работ
Рисунок 7. Пример. Автор24 — интернет-биржа студенческих работ
Рисунок 8. Пример. Автор24 — интернет-биржа студенческих работ
Рисунок 9. Пример. Автор24 — интернет-биржа студенческих работ
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 13 05 2021
Интегралы для чайников: как решать, правила вычисления, объяснение
Решение интегралов – задача легкая, но только для избранных. Эта статья для тех, кто хочет научиться понимать интегралы, но не знает о них ничего или почти ничего. Интеграл. Зачем он нужен? Как его вычислять? Что такое определенный и неопределенный интегралы?
Если единственное известное вам применение интеграла – доставать крючком в форме значка интеграла что-то полезное из труднодоступных мест, тогда добро пожаловать! Узнайте, как решать простейшие и другие интегралы и почему без этого никак нельзя обойтись в математике.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Изучаем понятие « интеграл »
Интегрирование было известно еще в Древнем Египте. Конечно, не в современном виде, но все же. С тех пор математики написали очень много книг по этой теме. Особенно отличились Ньютон и Лейбниц, но суть вещей не изменилась.
Как понять интегралы с нуля? Никак! Для понимания этой темы все равно понадобятся базовые знания основ математического анализа. Сведения о пределах и производных, необходимые и для понимания интегралов, уже есть у нас в блоге.
Неопределенный интеграл
Пусть у нас есть какая-то функция f(x).
Неопределенным интегралом функции f(x) называется такая функция F(x), производная которой равна функции f(x).
Другими словами интеграл – это производная наоборот или первообразная. Кстати, о том, как вычислять производные, читайте в нашей статье.
Первообразная существует для всех непрерывных функций. Также к первообразной часто прибавляют знак константы, так как производные функций, различающихся на константу, совпадают. Процесс нахождения интеграла называется интегрированием.
Простой пример:
Чтобы постоянно не высчитывать первообразные элементарных функций, их удобно свести в таблицу и пользоваться уже готовыми значениями.
Полная таблица интегралов для студентов
Определенный интеграл
Имея дело с понятием интеграла, мы имеем дело с бесконечно малыми величинами. Интеграл поможет вычислить площадь фигуры, массу неоднородного тела, пройденный при неравномерном движении путь и многое другое. Следует помнить, что интеграл – это сумма бесконечно большого количества бесконечно малых слагаемых.
В качестве примера представим себе график какой-нибудь функции.
Как найти площадь фигуры, ограниченной графиком функции? С помощью интеграла! Разобьем криволинейную трапецию, ограниченную осями координат и графиком функции, на бесконечно малые отрезки. Таким образом фигура окажется разделена на тонкие столбики. Сумма площадей столбиков и будет составлять площадь трапеции. Но помните, что такое вычисление даст примерный результат. Однако чем меньше и уже будут отрезки, тем точнее будет вычисление. Если мы уменьшим их до такой степени, что длина будет стремиться к нулю, то сумма площадей отрезков будет стремиться к площади фигуры. Это и есть определенный интеграл, который записывается так:
Точки а и b называются пределами интегрирования.
Бари Алибасов и группа
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Правила вычисления интегралов для чайников
Свойства неопределенного интеграла
Как решить неопределенный интеграл? Здесь мы рассмотрим свойства неопределенного интеграла, которые пригодятся при решении примеров.
Свойства определенного интеграла
Как считать определенный интеграл? С помощью формулы Ньютона-Лейбница.
Мы уже выяснили, что определенный интеграл – это предел суммы. Но как получить конкретное значение при решении примера? Для этого существует формула Ньютона-Лейбница:
Примеры решения интегралов
Ниже рассмотрим неопределенный интеграл и примеры с решением. Предлагаем самостоятельно разобраться в тонкостях решения, а если что-то непонятно, задавайте вопросы в комментариях.
Для закрепления материала посмотрите видео о том, как решаются интегралы на практике. Не отчаиваетесь, если интеграл не дается сразу. Обратитесь в профессиональный сервис для студентов, и любой тройной или криволинейный интеграл по замкнутой поверхности станет вам по силам.
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Сложные интегралы
Данная статья завершает тему неопределенных интегралов, и в неё включены интегралы, которые я считаю достаточно сложными. Урок создан по неоднократным просьбам посетителей, которые высказывали пожелания, чтобы на сайте были разобраны и более трудные примеры.
Предполагается, что читатель сего текста хорошо подготовлен и умеет применять основные приемы интегрирования. Чайникам и людям, которые не очень уверенно разбираются в интегралах, следует обратиться к самому первому уроку – Неопределенный интеграл. Примеры решений, где можно освоить тему практически с нуля. Более опытные студенты могут ознакомиться с приемами и методами интегрирования, которые в моих статьях еще не встречались.
Какие интегралы будут рассмотрены?
Сначала мы рассмотрим интегралы с корнями, для решения которых последовательно используется замена переменной и интегрирование по частям. То есть, в одном примере комбинируются сразу два приёма. И даже больше.
Затем мы познакомимся с интересным и оригинальным методом сведения интеграла к самому себе. Данным способом решается не так уж мало интегралов.
Третьим номером программы пойдут интегралы от сложных дробей, которые пролетели мимо кассы в предыдущих статьях.
В-четвертых, будут разобраны дополнительные интегралы от тригонометрических функций. В частности, существуют методы, которые позволяют избежать трудоемкой универсальной тригонометрической подстановки.
И в заключение рассмотрим интеграл от корня из дроби, в числителе и знаменателе которой находятся линейные функции.
Конечно, название урока не совсем точно, будут и не сказать, что сильно сложные интегралы. Тем не менее, крепких орешков предостаточно. Запланировано довольно много примеров, поэтому поехали.
Последовательная замена переменной и интегрирование по частям
Найти неопределенный интеграл
Подынтегральная функция представляет собой арктангенс, под которым находится кубический корень. Первая же мысль, которая приходит в голову – избавиться бы от этого корня. Данный вопрос решается путем замены переменной, сама техника замены специфична, и она подробно рассмотрена на уроке Интегралы от иррациональных функций. Проведем замену:
После такой замены у нас получится вполне симпатичная вещь:
Осталось выяснить, во что превратится 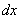
И само собой раскрываем дифференциалы:
На чистовике решение кратко записывается примерно так:
Проведем замену:
В результате замены получен знакомый тип интеграла, который интегрируется по частям:
(1) Выносим 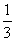
(2) В подынтегральной функции почленно делим числитель на знаменатель.
(3) Используем свойство линейности неопределенного интеграла. В последнем интеграле сразу подводим функцию под знак дифференциала.
(4) Берём оставшиеся интегралы. Обратите внимание, что в логарифме можно использовать скобки, а не модуль, так как 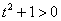
(5) Проводим обратную замену, выразив из прямой замены 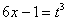
Студенты-мазохисты могут продифференцировать ответ и получить исходную подынтегральную функцию, как только что это сделал я. Нет-нет, я-то в правильном смысле выполнил проверку =)
Как видите, в ходе решения пришлось использовать даже больше двух приемов решения, таким образом, для расправы с подобными интегралами нужны уверенные навыки интегрирования и не самый маленький опыт.
На практике, конечно же, чаще встречается квадратный корень, вот три примера для самостоятельного решения:
Найти неопределенный интеграл
Найти неопределенный интеграл
Найти неопределенный интеграл
Данные примеры однотипны, поэтому полное решение в конце статьи будет только для Примера 2, в Примерах 3-4 – одни ответы. Какую замену применять в начале решений, думаю, очевидно. Почему я подобрал однотипные примеры? Часто встречаются в своем амплуа. Чаще, пожалуй, только что-нибудь вроде 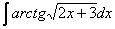
Но не всегда, когда под арктангенсом, синусом, косинусом, экспонентой и др. функциями находится корень из линейной функции, приходится применять сразу несколько методов. В ряде случаев удается «легко отделаться», то есть сразу после замены получается простой интеграл, который элементарно берётся. Самым легким из предложенных выше заданий является Пример 4, в нём после замены получается относительно несложный интеграл.
Методом сведения интеграла к самому себе
Остроумный и красивый метод. Немедленно рассмотрим классику жанра:
Найти неопределенный интеграл
Под корнем находится квадратный двучлен, и при попытке проинтегрировать данный пример чайник может мучаться часами. Такой интеграл берётся по частям и сводится к самому себе. В принципе не сложно. Если знаешь как.
Обозначим рассматриваемый интеграл латинской буквой 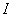
Интегрируем по частям:
(1) Готовим подынтегральную функцию для почленного деления.
(2) Почленно делим подынтегральную функцию. Возможно, не всем понятно, распишу подробнее:
(3) Используем свойство линейности неопределенного интеграла.
(4) Берём последний интеграл («длинный» логарифм).
Теперь смотрим на самое начало решения: 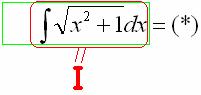
И на концовку:
Что произошло? В результате наших манипуляций интеграл свёлся к самому себе!
Приравниваем начало и конец:
Переносим 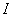
А двойку сносим в правую часть. В результате:
Или:
Константу 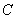
Примечание: Более строго заключительный этап решения выглядит так: 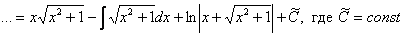
Таким образом: 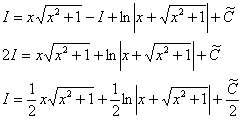
Константу 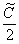
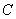
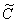
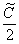
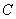
В результате:
Подобный трюк с переобозначением константы широко используется в дифференциальных уравнениях. И там я буду строг. А здесь такая вольность допускается мной только для того, чтобы не путать вас лишними вещами и акцентировать внимание именно на самом методе интегрирования.
Найти неопределенный интеграл
Еще один типовой интеграл для самостоятельного решения. Полное решение и ответ в конце урока. Разница с ответом предыдущего примера будет!
Если под квадратным корнем находится квадратный трехчлен, то решение в любом случае сводится к двум разобранным примерам.
Например, рассмотрим интеграл 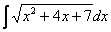
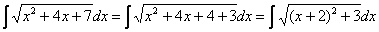
Далее проводится линейная замена, которая обходится «без всяких последствий»: 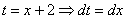
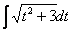
Или такой пример, с квадратным двучленом: 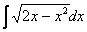
Выделяем полный квадрат: 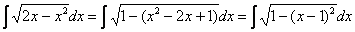
И, после линейной замены 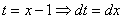
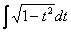
Рассмотрим еще два типовых примера на приём сведения интеграла к самому себе:
– интеграл от экспоненты, умноженной на синус;
– интеграл от экспоненты, умноженной на косинус.
В перечисленных интегралах по частям придется интегрировать уже два раза:
Найти неопределенный интеграл
Подынтегральная функция – экспонента, умноженная на синус.
Дважды интегрируем по частям и сводим интеграл к себе:

В результате двукратного интегрирования по частям интеграл свёлся к самому себе. Приравниваем начало и концовку решения:
Переносим 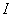
Готово. Попутно желательно причесать правую часть, т.е. вынести экспоненту за скобки, а в скобках расположить синус с косинусом в «красивом» порядке.
Теперь вернемся к началу примера, а точнее – к интегрированию по частям:
За 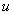
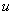
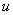
Почему такое возможно? Потому что экспонента превращается сама в себя (и при дифференцировании, и при интегрировании), синус с косинусом взаимно превращаются друг в друга (опять же – и при дифференцировании, и при интегрировании).
То есть, за 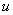
Найти неопределенный интеграл
Это пример для самостоятельного решения. Перед тем как решать, подумайте, что выгоднее в данном случае обозначить за 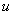
И, конечно, не забывайте, что большинство ответов данного урока достаточно легко проверить дифференцированием!
Примеры были рассмотрены не самые сложные. На практике чаще встречаются интегралы, где константа есть и в показателе экспоненты и в аргументе тригонометрической функции, например: 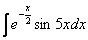
На завершающем этапе часто получается примерно следующее:
Даже в конце решения следует быть предельно внимательным и грамотно разобраться с дробями:
Интегрирование сложных дробей
Потихоньку подбираемся к экватору урока и начинаем рассматривать интегралы от дробей. Опять же, не все они суперсложные, просто по тем или иным причинам примеры были немного «не в тему» в других статьях.
Продолжаем тему корней
Найти неопределенный интеграл
В знаменателе под корнем находится квадратный трехчлен плюс за пределами корня «довесок» в виде «икса». Интеграл такого вида решается с помощью стандартной замены.
Решаем:
Замена тут проста:
Смотрим на жизнь после замены:
(1) После подстановки приводим к общему знаменателю слагаемые под корнем.
(2) Выносим 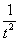
(3) Числитель и знаменатель сокращаем на 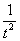
(4) Полученный интеграл, как вы помните из урока Интегрирование некоторых дробей, решается методом выделения полного квадрата. Выделяем полный квадрат.
(5) Интегрированием получаем заурядный «длинный» логарифм.
(6) Проводим обратную замену. Если изначально 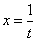
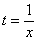
(7) Заключительное действие направлено на прическу результата: под корнем снова приводим слагаемые к общему знаменателю и выносим из-под корня 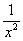
Найти неопределенный интеграл
Это пример для самостоятельного решения. Здесь к одинокому «иксу» добавлена константа, и замена почти такая же: 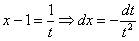
Единственное, что нужно дополнительно сделать – выразить «икс» из проводимой замены:
Полное решение и ответ в конце урока.
Иногда в таком интеграле под корнем может находиться квадратный двучлен, это не меняет способ решения, оно будет даже еще проще. Почувствуйте разницу:
Найти неопределенный интеграл
Найти неопределенный интеграл
Краткие решения и ответы в конце урока. Следует отметить, что Пример 11 является в точности биномиальным интегралом, метод решения которого рассматривался на уроке Интегралы от иррациональных функций.
Интеграл от неразложимого многочлена 2-й степени в степени
(многочлен в знаменателе)
Более редкий, но, тем не менее, встречающий в практических примерах вид интеграла.
Найти неопределенный интеграл
В знаменателе подынтегральной функции находится неразложимый на множители квадратный двучлен. Подчеркиваю, что неразложимость на множители является существенной особенностью. Если многочлен раскладывается на множители, то всё намного понятнее, например:
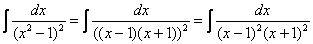
Но вернёмся к примеру со счастливым номером 13 (честное слово, не подгадал). Этот интеграл тоже из разряда тех, с которыми можно изрядно промучиться, если не знаешь, как решать.
Решение начинается с искусственного преобразования:
Как почленно разделить числитель на знаменатель, думаю, уже все понимают.
Полученный интеграл берётся по частям:
Для интеграла вида 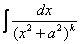
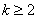
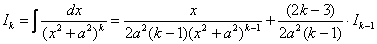
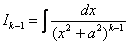
Убедимся в справедливости данной формулы для прорешанного интеграла 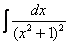
В данном случае: 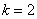
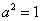
Как видите, ответы совпадают.
Найти неопределенный интеграл
Это пример для самостоятельного решения. В образце решения дважды последовательно использована вышеупомянутая формула.
Если под степенью находится неразложимый на множители квадратный трехчлен, то решение сводится к двучлену путем выделения полного квадрата, например:
Далее следует «безболезненная» линейная замена 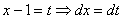
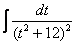
Что делать, если дополнительно в числителе есть многочлен? В этом случае используется метод неопределенных коэффициентов, и подынтегральная функция раскладывается в сумму дробей. Но в моей практике такого примера не встречалось ни разу, поэтому я пропустил данный случай в статье Интегралы от дробно-рациональной функции, пропущу и сейчас. Если такой интеграл все-таки встретится, смотрите учебник – там всё просто. Не считаю целесообразным включать материал (даже несложный), вероятность встречи с которым стремится к нулю.
Интегрирование сложных тригонометрических функций
Прилагательное «сложный» для большинства примеров вновь носит во многом условный характер. Начнем с тангенсов и котангенсов в высоких степенях. С точки зрения используемых методов решения тангенс и котангенс – почти одно и тоже, поэтому я больше буду говорить о тангенсе, подразумевая, что продемонстрированный прием решения интеграла справедлив и для котангенса тоже.
На уроке Интегралы от тригонометрических функций мы разобрали интеграл от тангенса в квадрате. На уроке Как вычислить площадь фигуры? в примере 10 фигурировал тангенс в кубе. В том примере для нахождения интеграла от тангенса в кубе мы применяли тригонометрическую формулу 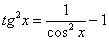
Найти неопределенный интеграл
Идея решения подобных интегралов состоит в том, чтобы с помощью формулы 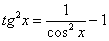
(1) Готовим подынтегральную функцию к применению формулы.
(2) Для одного из множителей используем формулу 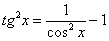
(3) Раскрываем скобки и сразу же используем свойство линейности неопределенного интеграла.
(4) В первом интеграле используем метод подведения функции под знак дифференциала. Во втором интеграле еще раз используем формулу 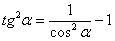
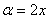
(5) Берём все три интеграла и получаем ответ.
Найти неопределенный интеграл
Это пример для самостоятельного решения. Для котангенса существует аналогичная формула: 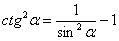
Если возникли затруднения или недопонимание, следует вернуться к уроку Интегралы от тригонометрических функций.
На вышеупомянутом уроке мы рассматривали универсальную тригонометрическую подстановку для решения определенного вида интегралов от тригонометрических функций. Недостаток универсальной тригонометрической подстановки заключается в том, что при её применении часто возникают громоздкие интегралы с трудными вычислениями. И в ряде случаев универсальной тригонометрической подстановки можно избежать!
Рассмотрим еще один канонический пример, интеграл от единицы, деленной на синус:
Найти неопределенный интеграл
Здесь можно использовать универсальную тригонометрическую подстановку и получить ответ, но существует более рациональный путь. Я приведу полное решение с комментами к каждому шагу:
(1) Используем тригонометрическую формулу синуса двойного угла 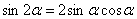
(2) Проводим искусственное преобразование: В знаменателе делим и умножаем на 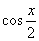
(3) По известной формуле в знаменателе превращаем дробь в тангенс.
(4) Подводим функцию под знак дифференциала.
(5) Берём интеграл.
Пара простых примеров для самостоятельного решения:
Найти неопределенный интеграл
Указание: Самым первым действием следует использовать формулу приведения 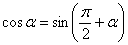
Найти неопределенный интеграл
Ну, это совсем простой пример.
Полные решения и ответы в конце урока.
Думаю, теперь ни у кого не возникнет проблем с интегралами:
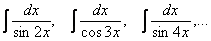
В чём состоит идея метода? Идея состоит в том, чтобы с помощью преобразований, тригонометрических формул организовать в подынтегральной функции только тангенсы и производную тангенса 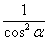
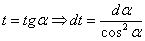
Аналогичные рассуждения, как я уже оговаривался, можно провести для котангенса.
Существует и формальная предпосылка для применения вышеуказанной замены:
Сумма степеней косинуса и синуса – целое отрицательное ЧЁТНОЕ число, например:
для интеграла 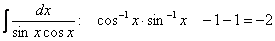
! Примечание: если подынтегральная функция содержит ТОЛЬКО синус или ТОЛЬКО косинус, то интеграл берётся и при отрицательной нечётной степени (простейшие случаи – в Примерах №№17, 18).
Рассмотрим пару более содержательных заданий на это правило:
Найти неопределенный интеграл
Сумма степеней синуса и косинуса 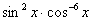
(1) Преобразуем знаменатель.
(2) По известной формуле получаем 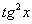
(3) Преобразуем знаменатель.
(4) Используем формулу 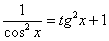
(5) Подводим функцию под знак дифференциала.
(6) Проводим замену 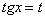
Далее берётся простой интеграл и проводится обратная замена.
Найти неопределенный интеграл
Это пример для самостоятельного решения.
Держитесь, начинаются чемпионские раунды =)
Зачастую в подынтегральной функции находится «солянка»:
Найти неопределенный интеграл
В этом интеграле изначально присутствует тангенс, что сразу наталкивает на уже знакомую мысль:
Искусственное преобразование в самом начале и остальные шаги оставлю без комментариев, поскольку обо всем уже говорилось выше.
Пара творческих примеров для самостоятельного решения:
Найти неопределенный интеграл
Найти неопределенный интеграл
Да, в них, конечно, можно понизить степени синуса, косинуса, использовать универсальную тригонометрическую подстановку, но решение будет гораздо эффективнее и короче, если его провести через тангенсы. Полное решение и ответы в конце урока
У многих читателей могло сложиться впечатления, что я немного подустал. Отнюдь. За окном февральский ветер – самая атмосфера для лекций. Естественно, данная страничка создана не за один день, я успел несколько раз побриться, регулярно кушаю и так далее. К тому же, загружать студентов – удовольствие бесконечное =). …Шутка! На самом деле моя миссия – разгружать посетителей сайта. Вагонами.
Переходим к заключительному пункту познавательного путешествия в мир сложных интегралов:
Интеграл от корня из дроби
Интеграл, который мы рассмотрим, встречается достаточно редко, но я буду очень рад, если единственный пример данного параграфа вам поможет.
Корнями всё начиналось, корнями и закончится. Рассмотрим неопределенный интеграл: 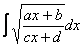
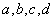
В подынтегральной функции у нас находится корень, а под корнем – дробь, в числителе и знаменателе которой располагаются линейные функции.
Метод стар – необходимо избавиться от корня. Стар и уныл, но сейчас станет веселее, поскольку придется проводить непростую замену.
Замена, с помощью которой мы гарантированно избавимся от корня, такова:
Теперь нужно выразить «икс» и найти, чему равен дифференциал 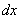
Выражаем «икс»:
Теперь найдем дифференциал:
Зачем были эти нелепые скучные телодвижения?
Я вывел готовые формулы, которыми можно пользовать при решении интеграла вида 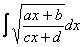
Формулы замены таковы:
Это было ни в коем случае не хвастовство, просто я не смог быстро найти эти формулы в близлежащей литературе и Сети – оказалось проще вывести. Да и может быть кто-нибудь для реферата возьмет.
Опять – двадцать пять, заключительный пример:
Найти неопределенный интеграл
Проведем замену:
В данном примере: 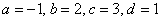
Таким образом:
Еще куда ни шло, могло всё оказаться значительно хуже. Такой интеграл, кстати, уже фигурировал в Примере 13. Интегрируем по частям:
Проведем обратную замену. Если изначально 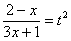
Некоторым страшно, а я это продифференцировал, ответ верный!
Иногда встречаются интегралы вида 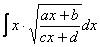
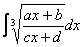
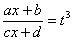
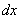
Теперь вам практически любой интеграл по силам, успехов!
Пример 2: Решение: 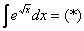
Проведем замену: 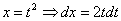
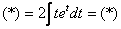
Интегрируем по частям: 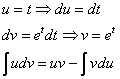
Пример 3: Ответ:
Пример 4: Ответ:
Пример 6: Решение: 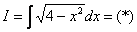
Интегрируем по частям: 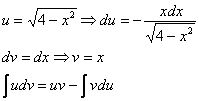

Таким образом: 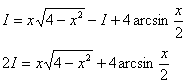
В результате:
Пример 8: Решение:
Дважды интегрируем по частям и сводим интеграл к себе: 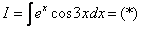
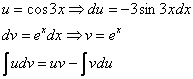
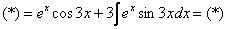
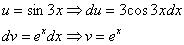
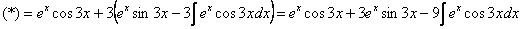
Таким образом:
Пример 10: Решение: 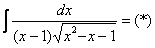
Проведем замену: 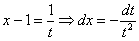
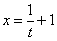
Пример 11: Решение: 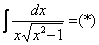
Замена: 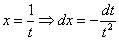
Пример 12: Решение: 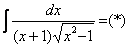
Замена: 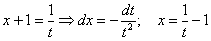
Пример 14: Решение: 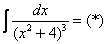
Дважды используем рекуррентную формулу 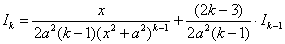
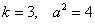
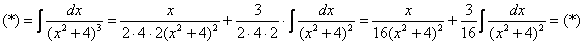
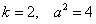
Пример 16: Решение:
Пример 18: Решение: 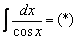
Используем формулу приведения: 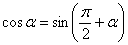
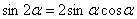
Пример 19: Решение:
Пример 21: Решение:
–3 – 3 = –6 – целое отрицательное ЧЁТНОЕ число
Пример 23: Решение:
Пример 24: Решение:
Автор: Емелин Александр
(Переход на главную страницу)

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5