Как находить количество точек экстремума

Максимумы, минимумы и экстремумы функций

Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.

Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.

Также можно сказать, что в этих точках меняется направление движения функции: если функция перестает падать и начинает расти – это точка минимума, наоборот – максимума.

Минимумы и максимумы вместе именуют экстремумами функции.

Иными словами, все пять точек, выделенных на графике выше, являются экстремумами.

В точках экстремумов (т.е. максимумов и минимумов) производная равна нулю.

Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.

Внимание! Когда пишут экстремумы или максимумы/минимумы имеют в виду значение функции т.е. \(y\). Когда пишут точки экстремумов или точки максимумов/минимумов имеют в виду иксы в которых достигаются максимумы/минимумы. Например, на рисунке выше, \(-5\) точка минимума (или точка экстремума), а \(1\) – минимум (или экстремум).

Как найти точки экстремумов функции по графику производной (7 задание ЕГЭ)?

Давайте вместе найдем количество точек экстремума функции по графику производной на примере:

Внимание! Если дан график производной функции, а нужно найти точки экстремумов функции, мы не считаем максимумы и минимумы производной! Мы считаем точки, в которых производная функции обращается в ноль (т.е. пересекает ось \(x\)).

Как найти точки максимумов или минимумов функции по графику производной (7 задание ЕГЭ)?

Чтобы ответить на этот вопрос, нужно вспомнить еще два важных правил:

— Производная положительна там, где функция возрастает.
— Производная отрицательна там, где функция убывает.

С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.

Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди \(-13\), \(-11\), \(-9\),\(-7\) и \(3\).

Чтобы проще было решать задачу расставим на рисунке сначала знаки плюс и минус, обозначающие знак производной. Потом стрелки – обозначающие возрастание, убывания функции.

\(-11\): производная сначала положительна, а потом отрицательна, значит функция возрастает, а потом убывает. Опять попробуйте это мысленно нарисовать и вам станет очевидно, что \(-11\) – это минимум.

\(- 9\): функция возрастает, а потом убывает – максимум.

Все вышесказанное можно обобщить следующими выводами:

— Функция имеет максимум там, где производная равна нулю и меняет знак с плюса на минус.
— Функция имеет минимум там, где производная равна нулю и меняет знак с минуса на плюс.

Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?

Чтобы ответить на этот вопрос, нужно делать все то же, что и в предыдущем пункте: находить где производная положительна, где отрицательна и где равна нулю. Чтобы было понятнее напишу алгоритм с примером решения:

Всё! Точки максимумов и минимумов найдены.

Изображая на оси точки в которых производная равна нулю – масштаб можно не учитывать. Поведение функции можно показать так, как это сделано на рисунке ниже. Так будет очевиднее где максимум, а где минимум.

Пример(ЕГЭ). Найдите точку максимума функции \(y=3x^5-20x^3-54\).
Решение:
1. Найдем производную функции: \(y’=15x^4-60x^2\).
2. Приравняем её к нулю и решим уравнение:

3. – 6. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:

Теперь очевидно, что точкой максимума является \(-2\).

Источник

Найти экстремумы функции

Данный калькулятор предназначен для нахождения экстремумов функции.
Следует различать понятия точек экстремума и экстремумов функции. Точки экстремума – точки максимума и минимума функции, это значения на оси Ox. Точка x₀ является точкой максимума функции y=f(x), если для всех x из ее окрестности выполняется неравенство f(x₀)≥f(x). Точка x₀ является точкой минимума функции y=f(x), если из ее окрестности для всех x выполняется неравенство f(x₀)≤f(x). Значения функции, которые соответствуют точкам экстремума, называются экстремумами функции, это значения на оси Oy.
Для того чтобы найти экстремумы функции можно использовать любой из трех условий экстремума, если функция удовлетворяет эти условиям.
Первым достаточным условием экстремума являются следующие утверждения: если в точке x₀ функция непрерывна, и в ней производная меняет знак с плюса на минус, то точка x₀ является точкой максимума, а если в данной точке производная меняет знак с минуса на плюс, то x₀ – точка минимума.

Вторым признаком экстремума является следующее утверждение: если производная второго порядка от x₀ больше нуля, то x₀ – точка минимума; если меньше нуля, то x₀ – точка максимума. Третье достаточное условие экстремума функции заключается в следующем. Пусть функция y=f(x) имеет производные до n-ого порядка в окрестности точки x0 и производные до n+1-ого порядка в самой точке x₀; пусть f’(x₀)= f’’(x₀)= f’’’(x₀)=…=f (n) ( x₀)=0 и f (n+1) ( x₀)≠0. Тогда, если n – нечетное, то x₀ – точка экстремума. Если f (n+1) ( x₀)>0, то x₀ – точка минимума, а, если f (n+1) ( x₀)

Источник

Возрастание и убывание функции на интервале, экстремумы

Чтобы определить характер функции и говорить о ее поведении, необходимо находить промежутки возрастания и убывания. Этот процесс получил название исследования функции и построения графика. Точка экстремума используется при нахождении наибольшего и наименьшего значения функции, так как в них происходит возрастание или убывание функции из интервала.

Данная статья раскрывает определения, формулируем достаточный признак возрастания и убывания на интервале и условие существования экстремума. Это применимо к решению примеров и задач. Следует повторить раздел дифференцирования функций, потому как при решении необходимо будет использовать нахождение производной.

Возрастание и убывание функции на интервале

Точки экстремума, экстремумы функции

Окрестностями точки х 0 считаются точки экстремума, а значение функции, которое соответствует точкам экстремума. Рассмотрим рисунок, приведенный ниже.

Экстремумы функции с набольшим и с наименьшим значением функции. Рассмотрим рисунок, приведенный ниже.

Достаточные условия возрастания и убывания функции

Чтобы найти максимумы и минимумы функции, необходимо применять признаки экстремума в том случае, когда функция удовлетворяет этим условиям. Самым часто используемым считается первый признак.

Первое достаточное условие экстремума

Иначе говоря, получим их условия постановки знака:

Алгоритм для нахождения точек экстремума

Чтобы верно определить точки максимума и минимума функции, необходимо следовать алгоритму их нахождения:

Рассмотрим алгоритм на примере решения нескольких примеров на нахождение экстремумов функции.

Так как второй интервал получился меньше нуля, значит, производная на отрезке будет отрицательной. Третий с минусом, четвертый с плюсом. Для определения непрерывности необходимо обратить внимание на знак производной, если он меняется, тогда это точка экстремума.

Точка х = 5 указывает на то, что функция является непрерывной, а производная поменяет знак с – на +. Значит, х=-1 является точкой минимума, причем ее нахождение имеет вид

Область определения функции – это все действительные числа. Это можно записать в виде системы уравнений вида:

После чего необходимо найти производную:

Точка х = 0 не имеет производной, потому как значения односторонних пределов разные. Получим, что:

Необходимо произвести вычисления для нахождения значения аргумента, когда производная становится равной нулю:

Изображение на прямой имеет вид

Значит, приходим к тому, что необходимо прибегнуть к первому признаку экстремума. Вычислим и получим, что

Перейдем к вычислению минимумов:

Произведем вычисления максимумов функции. Получим, что

Второй признак экстремума функции

Для начала находим область определения. Получаем, что

Необходимо продифференцировать функцию, после чего получим

Третье достаточное условие экстремума

Исходная функция – целая рациональная, отсюда следует, что область определения – все действительные числа. Необходимо продифференцировать функцию. Получим, что

Из выше решенного делаем вывод, что x 3 = 3 является точкой минимума функции.

Источник

Как находить количество точек экстремума

На рисунке изображен график производной функции определенной на интервале Найдите точку экстремума функции на интервале

Если производная в некоторой точке равна нулю, а в ее окрестности меняет знак, то это точка экстремума. На интервале график производной пересекает ось абсцисс, производная меняет знак с минуса на плюс. Следовательно, точка 2 является точкой экстремума.

На рисунке изображен график производной функции определенной на интервале Найдите точку экстремума функции на отрезке

Если производная в некоторой точке равна нулю, а в ее окрестности меняет знак, то это точка экстремума. На отрезке [−5; 0] график производной пересекает ось абсцисс в точке −1 при этом производная меняет знак с плюса на минус. Следовательно, точка −1 является точкой экстремума.

На рисунке изображен график производной функции f(x), определенной на интервале (−6; 5). Найдите точку экстремума функции f(x) на отрезке [−5; 4].

Если производная в некоторой точке равна нулю, а в ее окрестности меняет знак, то это точка экстремума. На отрезке [–5; 4] график производной пересекает ось абсцисс, производная меняет знак с минуса на плюс. Следовательно, точка −2 является точкой экстремума.

На рисунке изображен график производной функции f(x), определенной на интервале (−4; 8). Найдите точку экстремума функции f(x) на отрезке [−2; 6].

Если производная в некоторой точке равна нулю и меняет знак, то это точка экстремума. На отрезке [–2; 6] график производной пересекает ось абсцисс, производная меняет знак с плюса на минус. Следовательно, точка 4 является точкой экстремума.

На рисунке изображён график функции — производной функции определённой на интервале Найдите точку экстремума функции принадлежащую отрезку

Если производная в некоторой точке равна нулю, а в ее окрестности меняет знак, то это точка экстремума. На интервале [–1; 4] график производной пересекает ось абсцисс, производная меняет знак с минуса на плюс. Следовательно, точка 3 является точкой экстремума.

На рисунке изображён график функции — производной функции определённой на интервале Найдите точку экстремума функции принадлежащую отрезку

Если производная в некоторой точке равна нулю, а в ее окрестности меняет знак, то это точка экстремума. На интервале [0; 7] график производной пересекает ось абсцисс, производная меняет знак с минуса на плюс. Следовательно, точка 7 является точкой экстремума.

Найдите точку минимума функции

Найдите точку минимума функции

Найдем производную заданной функции:

Найдем нули производной:

Определим знаки производной функции и изобразим на рисунке поведение функции:

Искомая точка минимума

Найдите точку максимума функции

Область определения функции:

Найдите точку максимума функции

Найдем производную заданной функции:

Найдем нули производной:

Определим знаки производной функции и изобразим на рисунке поведение функции:

Искомая точка максимума

На рисунке изображен график производной функции определенной на интервале Найдите количество точек экстремума функции на отрезке

Точки экстремума соответствуют точкам смены знака производной. Производная меняет знак в точках 0; 2,2; 3. Тем самым, на отрезке [−4; 4] функция имеет 3 точки экстремума.

На рисунке изображен график производной функции определенной на интервале Найдите количество точек экстремума функции на отрезке

Точки экстремума соответствуют точкам смены знака производной. Производная меняет знак в точках −7, 3, 5. Тем самым, на отрезке [−4; 10] функция имеет 2 точки экстремума.

На рисунке изображен график производной функции f(x), определенной на интервале (−16; 4). Найдите количество точек экстремума функции f(x) на отрезке [−14; 2].

есть еще точка экстремума, это точка 3

Точка х=3 не входит в заданный промежуток

На рисунке изображен график производной функции f(x), определенной на интервале (−11; 11). Найдите количество точек экстремума функции f(x) на отрезке [−10; 10].

Точки экстремума соответствуют точкам смены знака производной. Производная меняет знак в точках −6, −2, 2, 6, 9. Тем самым, на отрезке [−10; 10] функция имеет 5 точек экстремума.

«Вершины» кривой и будут точками экстремума. В чем ошибка?

Дело в том, что на приведённом графике изображена не функция, а её производная. Поэтому экстремумы изображенной кривой — это экстремумы производной, а не самой функции.

На рисунке изображен график функции определенной на интервале Найдите сумму точек экстремума функции

Заданная функция имеет максимумы в точках 1, 4, 9, 11 и минимумы в точках 2, 7, 10. Поэтому сумма точек экстремума равна 1 + 4 + 9 + 11 + 2 + 7 + 10 = 44.

На рисунке изображен график функции f(x), определенной на интервале (−7; 4). Найдите сумму точек экстремума функции f(x).

Заданная функция имеет максимумы в точках −5, −2, 1, 3 и минимумы в точках −3, 0, 2. Поэтому сумма точек экстремума равна −5 − 2 + 1 + 3 − 3 + 0 + 2 = −4.

На рисунке изображен график функции y = f(x), определенной на интервале (−2; 12). Найдите сумму точек экстремума функции f(x).

Заданная функция имеет максимумы в точках 1, 4, 9, 11 и минимумы в точках 2, 7, 10. Поэтому сумма точек экстремума равна 1 + 4 + 9 + 11 + 2 + 7 + 10 = 44.

Ваше рассуждение было бы правильным, если бы это был график производной, но дан график функции.

На рисунке изображён график функции y = f(x), определённой на интервале (−8; 5). Найдите сумму точек экстремума функции f(x).

Заданная функция имеет максимумы в точках −5, 0, 2 и минимумы в точках −7, −1, 1, 3. Поэтому сумма точек экстремума равна −5 + 0 + 2 − 7 − 1 + 1 + 3 = −7.

Экстре́мум (лат. extremum — крайний) в математике — максимальное или минимальное значение функции на заданном множестве. Именно значений функции, а не аргумента.

Вы абсолютно правы

На рисунке изображён график функции y = f(x), определённой на интервале (−4; 8). Найдите сумму точек экстремума функции f(x).

Заданная функция имеет максимумы в точках −3, −1, 2, 4 и минимумы в точках −2, 1, 3, 5. Поэтому сумма точек экстремума равна −3 − 1 + 2 + 4 − 2 + 1 + 3 + 5 = 9.

Найдите точку максимума функции

Квадратный трехчлен с отрицательным старшим коэффициентом достигает наибольшего значения в точке в нашем случае — в точке Функция в этой точке определена. Поскольку логарифмическая функция с основанием, большим единицы, возрастает, то — точка максимума функции.

Источник

Узнать ещё

Знание — сила. Познавательная информация

Точки экстремума на графике производной

Рассмотрим примеры заданий из №7 ЕГЭ, в которых нужно найти точки экстремума на графике производной.

Точка x_o, в которой существует производная f'(x_o), является точкой экстремума функции f(x), если производная в этой точке равна нулю и при переходе через x_o производная меняет свой знак.

Отсюда следует, что в точках экстремума функции график производной должен не просто касаться оси Ox, он должен её пересекать.

На рисунке изображён график производной функции f(x), определённой на интервале (-6;7). Найти точку экстремума функции f(x) на отрезке [-2;5].

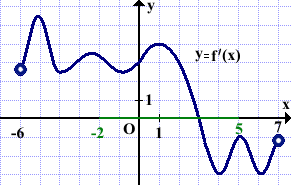
Решение:

На рисунке изображён график производной (а не график функции)!

В точках экстремума функции производная f'(x) равна нулю и меняет знак.

Выделяем отрезок [-2;5]. Точка, в которой производная равна нулю и меняет знак — это точка с абсциссой 3.

Значит x=3 — точка экстремума функции y=f(x).

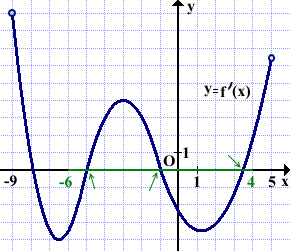
На рисунке изображён график производной функции f(x), определённой на интервале (-9;5). Найти количество точек экстремума функции f(x) на отрезке [6-;4].

Выделяем отрезок [-6;4].

На этом отрезке график производной пересекает ось абсцисс в трёх точках.

Следовательно, на отрезке [-6;4] функция f(x) имеет три точки экстремума.

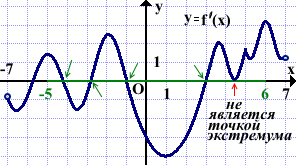
На рисунке изображён график производной функции f(x), определённой на интервале (-7;7). Найти количество точек экстремума функции f(x) на отрезке [-5;6].

Выделяем отрезок [-5;6].

На этом отрезке график производной пересекает ось абсцисс в четырёх точках. Значит, функция f(x) имеет на отрезке [-5;6] четыре точки экстремума.

Точка, в которой производная равна нулю, но знак не меняет (график производной коснулся оси Ox, но не пересёк её), не является точкой экстремума.

Важно внимательно читать условие, чтобы не перепутать нахождение точек экстремума по графику производной с заданием на нахождение точек экстремума по графику функции!

Источник