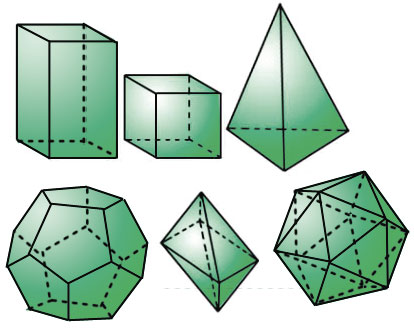
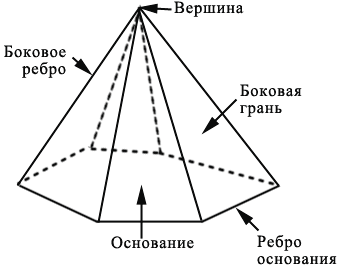
Как находить координаты вершин параллелепипеда

Прямоугольный параллелепипед. Пирамида.

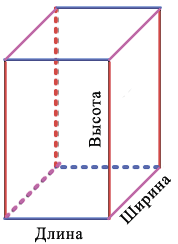
Измерения имеют названия: длина, ширина, высота. Данные названия введены, чтобы различать измерения:

Частным случаем прямоугольного параллелепипеда является куб. Куб — это прямоугольный параллелепипед, все измерения которого равны:

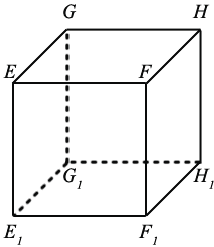
EFHGE₁F₁H₁G₁ — куб, его высота, ширина и длина равны. Гранями куба являются 6 равных квадратов.

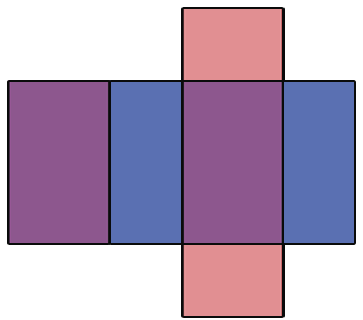
Рассмотрим следующую фигуру:

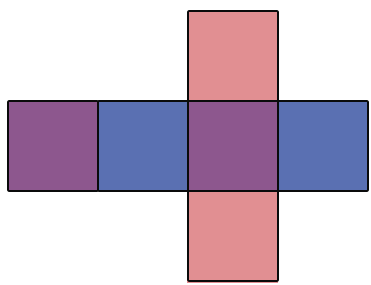
Данная фигура состоит из шести прямоугольников, которые попарно равны (выделены одним цветом). Если мы согнём по линиям данную фигуру и склеим, то получим модель прямоугольного параллелепипеда, противоположные грани которого будут одного цвета. Рассматриваемую фигуру называют развёрткой прямоугольного параллелепипеда. Как сказано выше, куб состоит из 6 равных квадратов, значит, его развертка будет иметь следующий вид:

В данном случае куб «разрезали» по 6 горизонтальным ребрам и 1 вертикальному, при этом противоположные грани выделены одним цветом. Таким образом, «разрезая» любой многогранник по ребрам так, чтобы все грани оказались в одной плоскости, можно получить его развертку. Развертки многогранников нужны, например, для создания их объемных моделей.

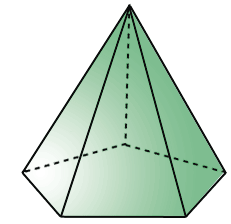
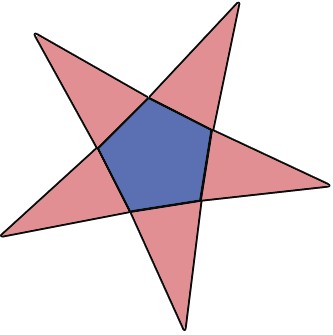
Если мы «разрежем» по боковым рёбрам пятиугольную пирамиду, то получим следующий многоугольник, который будет являться развёрткой данной пирамиды:

Поделись с друзьями в социальных сетях:

Источник

Геометрия

Лучшие условия по продуктам Тинькофф по этой ссылке

Дарим 500 ₽ на баланс сим-карты и 1000 ₽ при сохранении номера

. 500 руб. на счет при заказе сим-карты по этой ссылке

Лучшие условия по продуктам
ТИНЬКОФФ по данной ссылке

План урока:

Прямоугольная система координат

В планиметрии мы уже рассматривали прямоугольную систему координат. Ее образовывали 2 перпендикулярные друг другу оси – Ох и Оу. С ее помощью можно было определить положение любой точки на координатной плоскости, просто указав две ее координаты – абсциссу х и ординату у.

В стереометрии необходимо определять положение точки уже не на плоскости, а в пространстве. Для этого добавляется третья ось Оz, которую ещё называют осью апликат. Каждые пара осей образует свою отдельную координатную плоскость, всего получается три таких плос-ти: Оху, Охz и Oуz.

Точка О именуется началом координат. Она делит каждую ось на два луча, один из которых – это положительная полуось, а второй – отрицательная полуось.

Для каждой точки в пространстве можно указать три координаты, однозначно определяющие ее положение в пространстве. Пусть в пространстве есть некоторая точка М. Опустим из нее перпендикуляры на координатные плоскости. В свою очередь из этих проекций точки М опустим перпендикуляры уже на координатные оси. В результате будет построен прямоугольный параллелепипед. Измерения этого параллелепипеда и будут координатами точки М:

Если точка M находится в одной из координатных плоскостей, то одна из ее координат будет нулевой. Например, если М принадлежит плоскости Охz, то нулю будет равна координата у. Если же точка располагается на одной из координатных осей, то у нее уже две координаты будут нулевыми. Так, если точка находится на оси Ох, то только координата х может быть ненулевой, а у и z окажутся нулевыми координатами.

На показанном рисунке ребра параллелепипеда лежат на положительных полуосях, поэтому все координаты положительны. Если же какие-то ребра будут лежать на отрицательных полуосях, то и соответствующие координаты будут отрицательными.

Координаты вектора

Введем в пространстве прямоугольную систему коорд-т, а далее от ее начала отложим вектора i, j и k, которые соответственно будут лежать на координатных осях Ох, Оу и Оz, и длина которых составит единицу. Эти вектора именуют координатными векторами, единичными векторами или просто ортами.

Ясно, что орты находятся в разных плоскостях, то есть они образуют тройку некомпланарных векторов. Это означает, что любой вектор а в пространстве можно разложить на орты:

где х, у и z – какие-то действительные числа. Они как раз и считаются координатами вектора а. Записываются коорд-ты вектора в фигурных скобках. На следующем рисунке показан вектор а<3; – 2; – 4>.

Задание. Разложите на орты вектор

Если начало вектора ОМ располагается в начале системы координат О, то вектор ОМ именуют радиус-вектором. В таком случае коорд-ты точки конца вектора, то есть точки М, совпадают с коорд-тами самого вектора ОМ.

Это свойство радиус-вектора мы уже изучали в 9 классе в планиметрии, и в стереометрии оно сохраняется.

Задание. О – начало координат, а точка М имеет коорд-ты (2; 5; – 3). Найдите коорд-ты вектора ОМ.

Решение. Всё очень просто – коорд-ты вектора будут совпадать с коорд-тами его конца, так его начало совпадает с началом коорд-т:

Также в стереометрии остаются справедливыми ещё несколько правил, которые были доказаны в курсе планиметрии:

Задание. Найдите сначала сумму, а потом разность векторов а <3; 7; 5>и b<2; 4; 6>.

Решение. Будем обозначать коорд-ты векторов через индексы. Например, коорд-ты вектора а – это х_а, у_а и z_а. Пусть сумма векторов будет вектором с, а их разность – вектором d. Для вычисления суммы надо складывать соответствующие координаты:

Для вычисления разности надо из коорд-т вектора а вычитать коорд-ты вектора b:

Задание. Вычислите коорд-ты вектора р, зная, что:

Решение. Для вычисления координат надо в выражении для вектора р сами векторы заменить на их координаты:

Получается, что вектор p имеет координаты <0; – 2; 3>.

Теперь мы можем доказать ещё одно утверждение, уже известное из курса планиметрии:

Действительно, пусть есть некоторый вектор АВ, причем коорд-ты точек А и В известны. Построим радиус-вектора OА и OВ:

Координаты радиус-векторов будут совпадать с координатами их концов:

Задание. Определите коорд-ты вектора CD, если даны коорд-ты точек С и D: С(3; 8; – 5) и D(5; 4; 1).

Решение. Здесь надо просто из коорд-т точки D, являющейся концом вектора, вычесть коорд-ты точки С:

Задание. От точки K(10; 6; 13) отложен вектор m<3; 2; 5>, конец совпал в точку H. Найдите коорд-ты точки H.

Решение. Коорд-ты вектора m и его концов связаны формулами:

Координаты середины отрезка

Пусть в пространстве есть отрезок АВ, и координаты его концов известны. Точка М – середина этого отрезка. Как вычислить ее координаты? Рассмотрим взаимосвязь векторов АМ, МВ и АВ:

Раз М – середина АВ, то вектора АМ и МВ имеют равные длины, и при этом они находятся на одной прямой. Значит, эти вектора равны и потому у них одинаковые коорд-ты:

Аналогично можно получить аналогичные формулы для коорд-т у и z:

Рассмотрим несколько задач на координаты точек.

Задание. Найдите коорд-ты середины отрезка, соединяющего точки А(3; 7; 12) и В(1; 5; – 4).

Решение. Просто используем только что выведенные формулы. Середину также обозначаем буквой М:

Задание. Известно, что K середина отрезка CD. Даны координаты точек С и K: С(12; 9; – 3) и K(15; 7; 3). Найдите коорд-ты D.

Решение. Сначала запишем формулу для коорд-ты х:

Вычисление длины векторов и расстояния между точками

Рассмотрим радиус-вектор ОМ с коорд-тами . Попытаемся найти его длину. Мы можем построить прямоугольный параллелепипед, в котором этот вектор окажется диагональю:

Напомним, что квадрат длины диагонали в прямоугольном параллелепипеде равен сумме квадратов его измерений. Но в полученном параллелепипеде измерения – это коорд-ты х, у и z, поэтому можно записать:

Так как равные вектора имеют как одинаковы и коорд-ты, и длина, то ясно, что каждый вектор с коорд-тами будет равен рассмотренному радиус-вектору, а значит и его длина будет рассчитываться по такой же формуле.

Задание. Найдите длину вектора m<– 2; 9; 6>.

Решение. Просто используем формулу:

Рассмотрим отрезок АВ с известными коорд-тами его концов. Можно построить вектор АВ, его коорд-ты будут определяться так:

Задание. Найдите расстояние между точкой K(10; 15; 5) и M(16; 21; – 2).

Решение. Просто подставляем коорд-ты точек в формулу:

Задание. Найдите длину медианы KM в ∆ KPN, если известны коорд-ты его вершин: P(2; 5; 8), N (6; 9; 12) и K(16; 11; 13).

Решение. Для нахождения длины медианы достаточно знать коорд-ты ее концов. Коорд-ты K уже известны, а M – середина PN, что позволяет вычислить и ее коорд-ты:

Коллинеарность векторов

Напомним, что если два вектора а и b коллинеарны друг другу, то должно существовать такое число k, что

Полученное отношение (1) является одновременно и признаком коллинеарных векторов, и их свойством. Слово «признак» означает, что любые вектора, чьи координаты соответствуют условию (1), будут коллинеарны. Слово «свойство» означает обратное – если известно, что вектора коллинеарны, то для них обязательно выполняется условие (1). В таких случаях в математике может использоваться словосочетание «тогда и только тогда»:

Очень важно то, что это правило действует только в случае, если все коорд-ты векторов ненулевые. Теперь рассмотрим случай, когда какие-то коорд-ты вектора b (одна или две из них) равны нулю. Например, пусть

В результате мы выяснили, что если коорд-та одного вектора нулевая, то и у любого вектора, коллинеарному ему, эта же коорд-та также должна быть нулевой. Особняком стоит случай с нулевым вектором с коорд-тами <0; 0; 0>. Он условно признается коллинеарным любому вектору.

Задание. Выясните, какие из этих пар векторов коллинеарны:

Решение. В первом задании просто делим друг на друга соответствующие коорд-ты и находим значение коэффициента k:

Значение коэффициента k оказалось одинаковым для каждой пары коорд-т, значит, вектора коллинеарны.

Повторяем эти действия в задании б):

На этот раз коэффициенты k оказались различными, значит, вектора неколлинеарны.

В задании в) у вектора е коорд-та z нулевая. Значит, если и у вектора f, если он коллинеарен z, эта координата должна быть нулевой, но это не так. Значит, вектора e и f неколлинеарны.

В задании г) снова указаны вектора с нулевыми коорд-тами. Но у обоих векторов коорд-та z нулевая, поэтому они могут быть коллинеарными. Однако необходимо проверить, что отношение ненулевых координат одинаково:

Коэффициент k получился одинаковым, поэтому вектора коллинеарны.

В последнем задании д) вектор n – нулевой, ведь все его коорд-ты нулевые. Нулевой вектор всегда коллинеарен другим векторам, в том числе и в этом задании.

Ответ: а) да; б) нет; в) нет; г) да; д) да.

Задание. Выясните, располагаются ли на одной прямой точки А(3; 5; 12), В(5; 7; 16) и С(0; 2; 6).

Решение. Ясно, что если эти точки находятся на одной прямой, то вектора АВ и ВС будут коллинеарными. Если же эти вектора неколлинеарны, то и точки должны находиться на разных прямых.

Сначала вычислим коорд-ты векторов АВ и ВС:

Теперь проверяем, коллинеарны ли эти вектора:

Коэффициенты k одинаковы, а потому АВ и ВС – коллинеарные векторы. Значит, точки А, В и С находятся на одной прямой.

Определение компланарности векторов

Пусть у нас есть три вектора с известными коорд-тами:

Как определить, компланарны ли эти вектора, то есть располагаются ли они в одной плоскости? Если эти вектора компланарны, то, по признаку компаланарности, вектор а можно разложить на вектора b и с:

где х и y – некоторые числа. Но если такое разложение существует, то коорд-ты векторов а, b и с будут связаны равенствами:

Получили систему из 3 уравнений с двумя неизвестными (х и y). Если такая система имеет решение, то вектора компланарны. Если же решения нет, то вектора не компланарны.

Задание. Определите, компланарны ли вектора

Имеем систему с тремя уравнениями. Из последних двух уравнений очевидно, что его решением может быть только пара чисел:

Значит, рассмотренная тройка векторов компланарна.

Задание. Располагаются ли в одной плос-ти вектора:

Решение. Нам надо проверить компаланарность векторов, поэтому действуем также, как и в предыдущей задаче. Если вектора компланарны, то существует разложение:

Получилось неверное равенство. Это означает, что у системы уравнений решения нет, и потому тройка векторов некомпланарна.

Скалярное произведение векторов

В 9 классе мы уже изучали скалярное произведение векторов.

Для нахождения угла между векторами необходимо отложить их от одной точки, тогда они образуют такой угол.

Задание. Угол между векторами с и d составляет 60°, а их длины соответственно равны 5 и 6. Найдите их скалярное произведение.

Решение. Здесь для расчета просто перемножаем длины векторов и косинус 60°:

Напомним несколько уже известных нам фактов о скалярном произведении, остающихся верными и в стереометрии:

Формула для расчета скалярного произведения по коорд-там векторов, используемая в стереометрии, несколько отличается от формулы из курса планиметрии. Напомним, что в планиметрии произведение векторов аа; у_а> и b<х_b; y_b> можно было рассчитать так:

Задание. Вычислите скалярное произведение векторов:

На практике скалярное произведение обычно используется для расчета углов между векторами, а также отрезками и прямыми. Рассмотрим несколько задач.

Задание. Вычислите угол между векторами:

Теперь через скалярное произведение возможно рассчитать косинус искомого нами угла, а затем и сам угол, который мы обозначим как α:

Задание. Рассчитайте углы в ∆АВС, зная коорд-ты его вершин: А(1; – 1; 3), В(3; – 1; 1) и С(– 1; 1; 3).

Решение. Чтобы найти ∠В, необходимо просто рассчитать угол между векторами ВС и ВА также, как это сделано в предыдущей задаче. Но сначала найдем коорд-ты векторов ВС и ВА и их длины:

Далее рассчитываем скалярное произведение векторов:

Теперь найдем угол А, который представляет собой угол между векторам AВ и AС. Вектор AВ – это вектор, противоположный ВA, то у него та же длина, но противоположный знак у коорд-т:

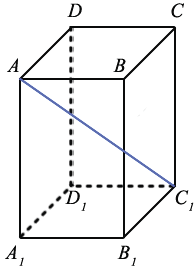
Задание. В прямоугольном параллелепипеде АВСDA₁B₁C₁D₁ ребра имеют длину:

Рассчитайте угол между векторами DB₁ и BC₁.

Решение. Введем систему коорд-т Охуz и расположим в нем параллелепипед следующим образом:

При этом построении граничные точки векторов будут иметь следующие коорд-ты:

Находим коорд-ты векторов, а также их длины:

Рассчитываем скалярное произведение DB₁ и BC₁:

Получили ноль. Из этого вытекает, что вектора перпендикулярны, то есть искомый нами угол составляет 90°.

Сегодня мы научились использовать координаты для решения стереометрических задач. Почти все формулы, используемые в методе координаты, аналогичны тем формулам, которые были выведены ещё в курсе планиметрии. Надо лишь учитывать существование ещё одной, третьей координаты z.

Источник

Принадлежность точки параллелепипеду

Представим себе плоскоть, проходящую через одну из граней параллелепипеда.
Ту часть пространства, которой принадлежит сам параллелепипед, можно задать неравенством относительно уравнения плоскости грани.

Таким образом параллелепипед может быть задан 6 неравенствами относительно своих граней.

Если координаты произвольной точки будут удовлетворять все этим неравенствам, то точка находится внутри параллелепипеда.

Можно попробовать второй вариант:

Соединим все вершины с заданной точкой.

Мы получим 6 пирамид с вершмнами в заданной точке и основаниями в виде граней параллелепипеда. Определим суммарный объем этих пирамид и сравним его с объемом всего заданного параллелепипеда.

Если точка находися внутри то суммарный объем будет равен объему параллелепипеда. Если суммарный объем больше, то точка находится снаружи.

Можно предложить еще один вариант:

Найти расстояние от заданной точки до всех граней параллелепипеда. Если хотябы одно из расстояний будет больше расстояния между любой парой противоположных граней, то точка находится вне параллелепипеда.

P.S. Мне пока наравится первый вариант. Там достаточно составить всего 6 уравнений плоскостей граней.

Поместить начало координат в одну из вершин параллелепипеда, а оси направить вдоль трех взаимно перпендикулярных ребер. Т. е. по сути преобразованиями получить новую систему координат.

И в этой системе координат определить новые координаты вершин и заданной точки. Теперь сравнив координаты точки и вершин всегда можно будет сказать где находится точка.

Слушай, начни с отрезка. Потом возьми прямоугольник. Потом уж разберешься с параллелепипедом. Все очень просто.

А потом насобачишься настолько, что и с четырехмерными фигурами будешь как орешки щелкать. ))))

Источник

Прямоугольный параллелепипед. Что это такое?

Определение параллелепипеда

Начнем с того, что узнаем, что такое параллелепипед.

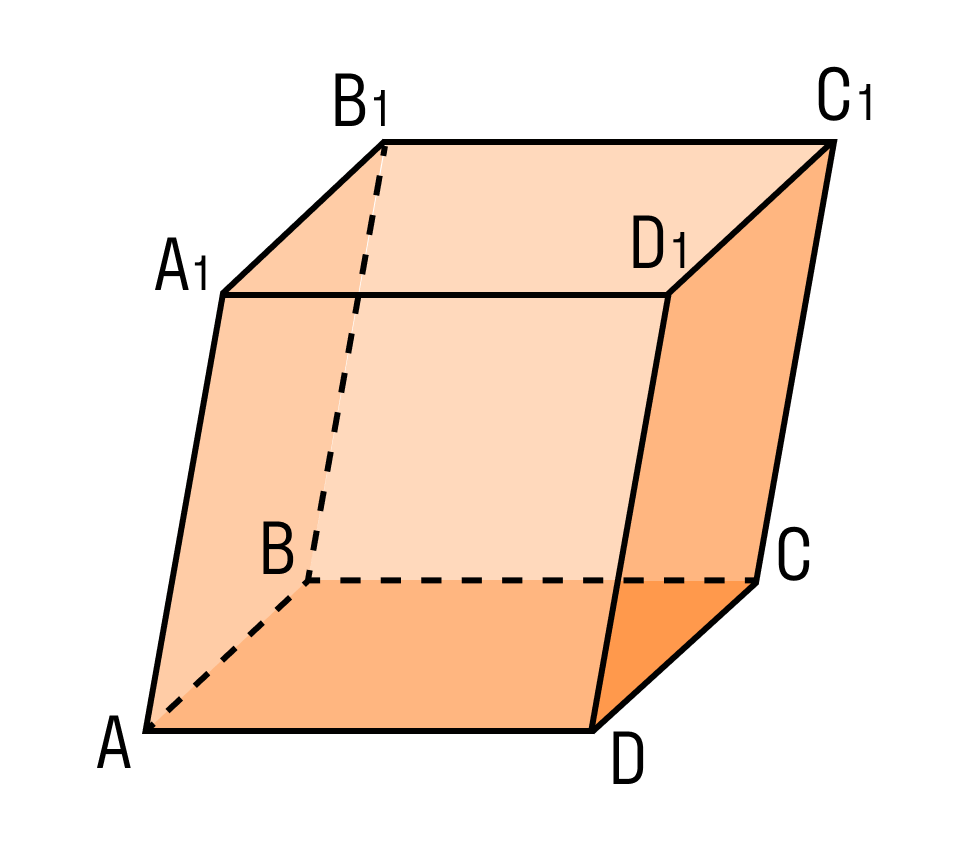
Параллелепипедом называется призма, основаниями которой являются параллелограммы. Другими словами, параллелепипед — это многогранник с шестью гранями. Каждая грань — параллелограмм.

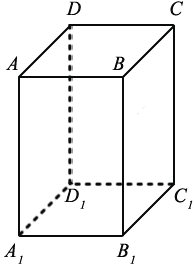
На рисунке два параллелограмма АВСD и A₁B₁C₁D₁. Основания параллелепипеда, расположены параллельно друг другу в плоскостях. А боковые ребра АA₁, ВB₁, CC₁, DD₁ параллельны друг другу. Образовавшаяся фигура — параллелепипед.

Внимательно рассмотрите, как выглядит параллелепипед и каковы его составляющие.

Когда пересекаются три пары параллельных плоскостей, образовывается параллелепипед.

Основанием параллелепипеда является, в зависимости от его типа: параллелограмм, прямоугольник, квадрат.

Параллелепипед — это:

Свойства параллелепипеда

Быть параллелепипедом ー значит неотступно следовать законам геометрии. Иначе можно скатиться до простого параллелограмма.

Вот 4 свойства параллелепипеда, которые необходимо запомнить:

Подготовка к ЕГЭ по математике онлайн в школе Skysmart — отличный способ освежить знания и снять стресс перед экзаменом.

Прямой параллелепипед

Прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию.

Основание прямого параллелепипеда — параллелограмм. В прямом параллелепипеде боковые грани — прямоугольники.

Свойства прямого параллелепипеда:

На слух все достаточно занудно и сложно, но на деле все свойства просто описывают фигуру. Внимательно прочтите вслух каждое свойство, разглядывая рисунок параллелепипеда после каждого пункта. Все сразу встанет на места.

Формулы прямого параллелепипеда:

Прямоугольный параллелепипед

Определение прямоугольного параллелепипеда:

Прямоугольным параллелепипедом называется параллелепипед, у которого основание — прямоугольник, а боковые ребра перпендикулярны основанию.

Внимательно рассмотрите, как выглядит прямоугольный параллелепипед. Отметьте разницу с прямым параллелепипедом.

Свойства прямоугольного параллелепипеда

Прямоугольный параллелепипед обладает всеми свойствами произвольного параллелепипеда.

Формулы прямоугольного параллелепипеда:

Диагонали прямоугольного параллелепипеда: теорема

Не достаточно просто знать свойства прямоугольного параллелепипеда, нужно уметь их доказывать.

Если есть теорема, нужно ее доказать. (с) Пифагор

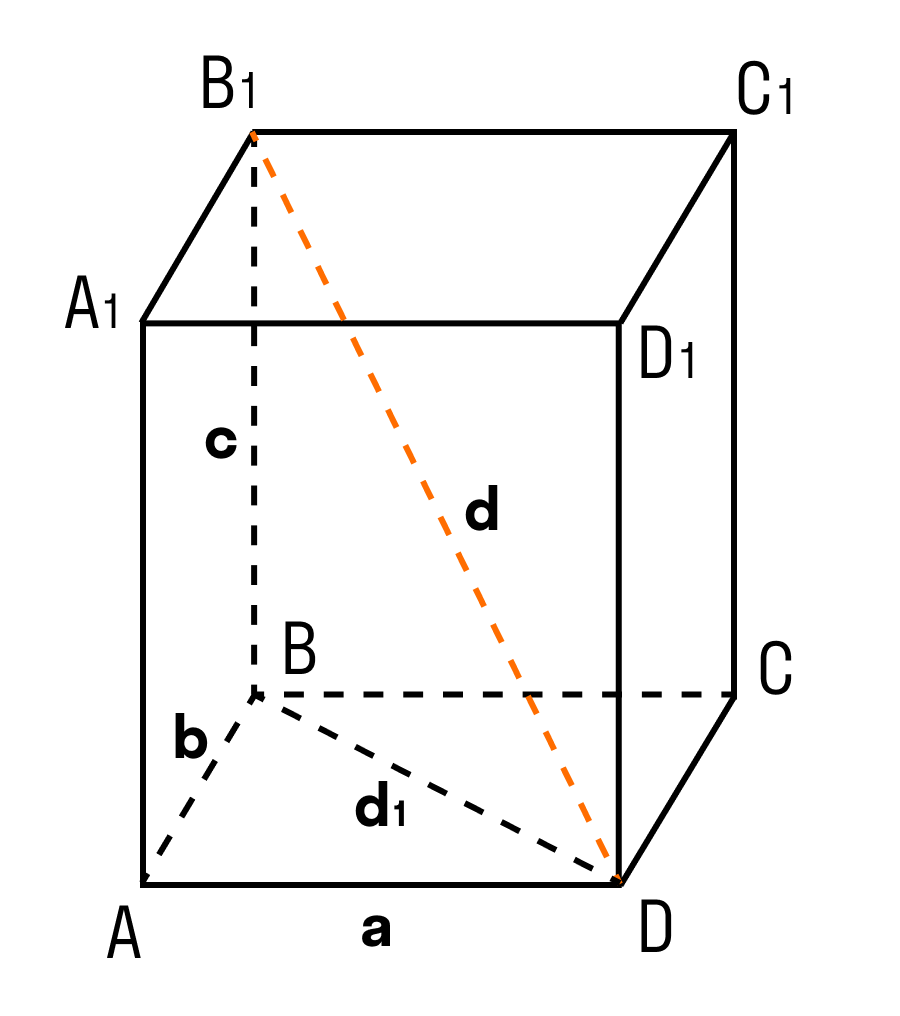
Теорема: Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.

В данном случае, три измерения — это длина, ширина, высота. Длина, ширина и высота — это длины трех ребер, исходящих из одной вершины прямоугольного параллелепипеда.

Дан прямоугольный параллелепипед ABCDA₁B₁C₁D₁. Доказать теорему.

Доказательство теоремы:

Чтобы найти диагональ прямоугольного параллелепипеда, помните, что диагональ — это отрезок, соединяющий противоположные вершины.

Все грани прямоугольного параллелепипеда — прямоугольники.

ΔABD: ∠BAD = 90°, по теореме Пифагора

ΔB₁BD: ∠B₁BD = 90°, по теореме Пифагора

d² = a² + b² + c²

Доказанная теорема — пространственная теорема Пифагора.

Куб: определение, свойства и формулы

Кубом называется прямоугольный параллелепипед, все три измерения которого равны.

Каждая грань куба — это квадрат.

Свойства куба:

Помимо основных свойств, куб характеризуется умением вписывать в себя тетраэдр и правильный шестиугольник.

Формулы куба:

Решение задач

Чтобы считать тему прямоугольного параллелепипеда раскрытой, стоит потренироваться в решении задач. 10 класс — время настоящей геометрии для взрослых. Поэтому, чем больше практики, тем лучше. Разберем несколько примеров.

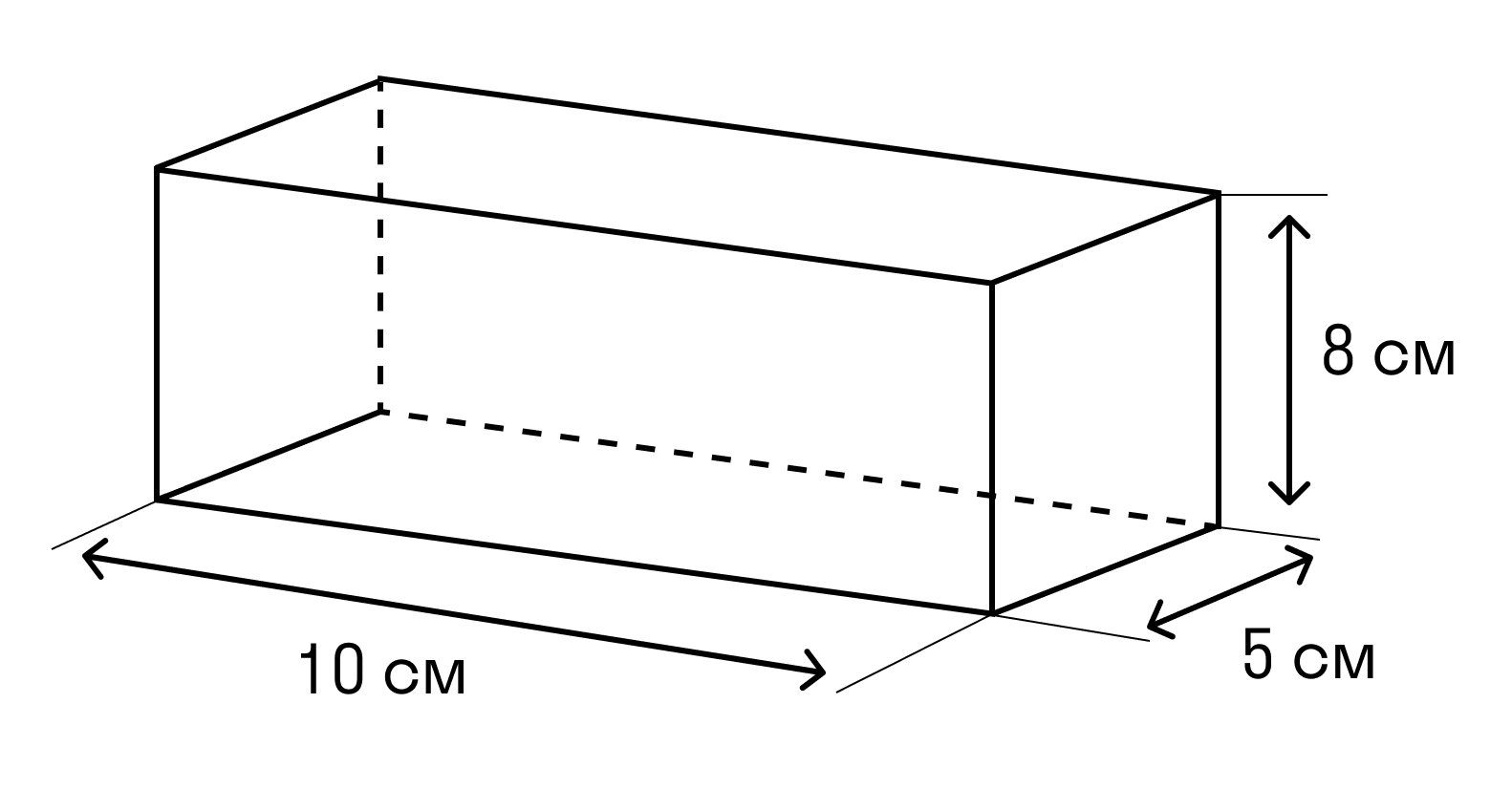
Задачка 1. Дан прямоугольный параллелепипед. Нужно найти сумму длин всех ребер параллелепипеда и площадь его поверхности.

Формула нахождения площади поверхности параллелепипеда Sп.п = 2(ab+bc+ac).
Тогда: S = (5*8 + 8*10 + 5*10) * 2 = 340 см2.

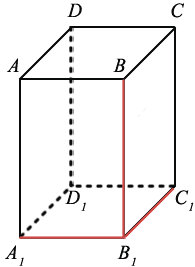
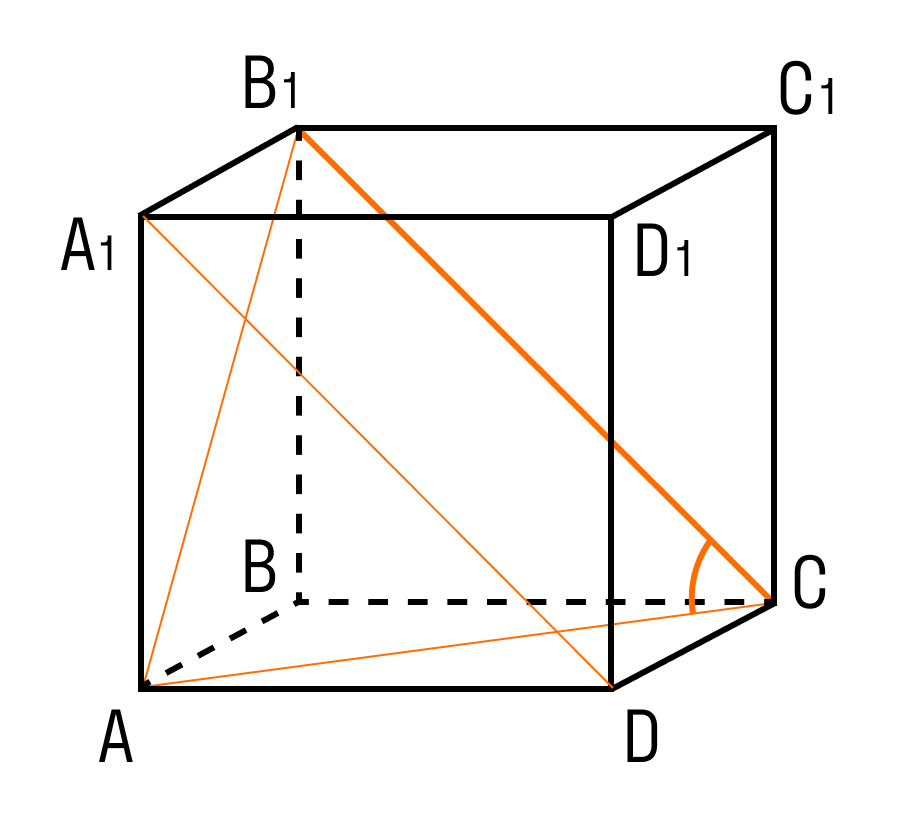
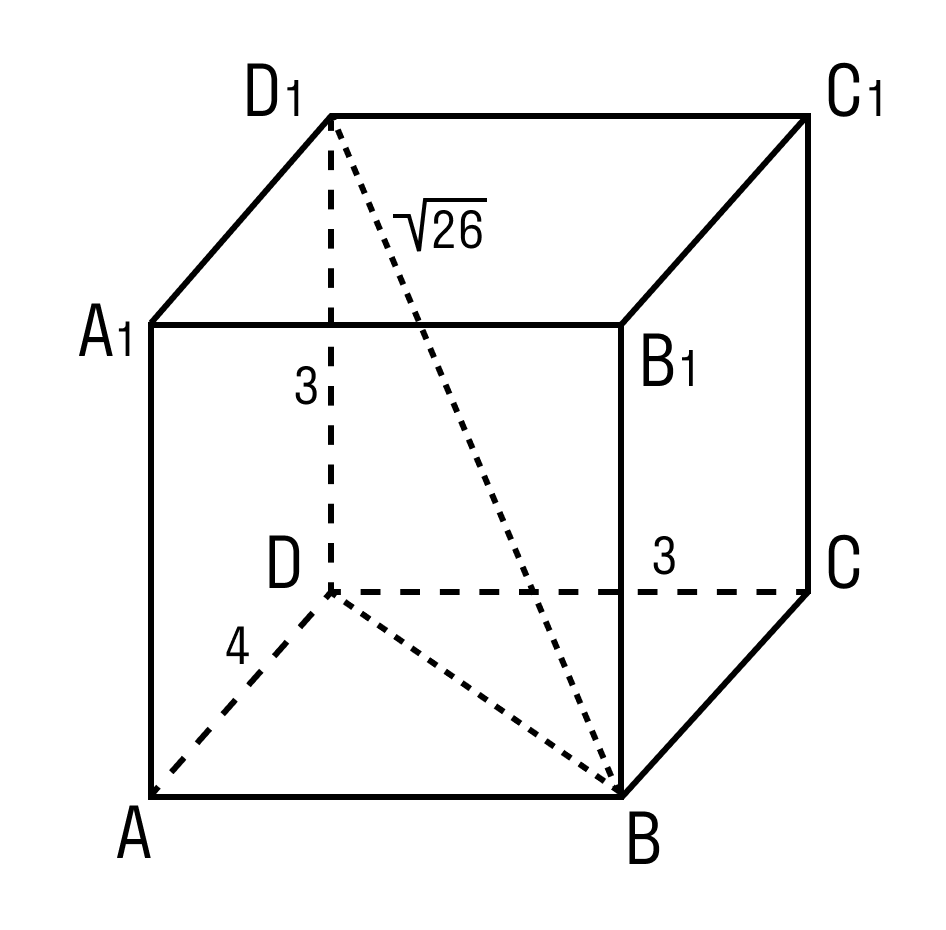
Задачка 2. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

Нужно найти длину ребра A₁B₁.

В фокусе внимания треугольник BDD1.
Угол D = 90°.

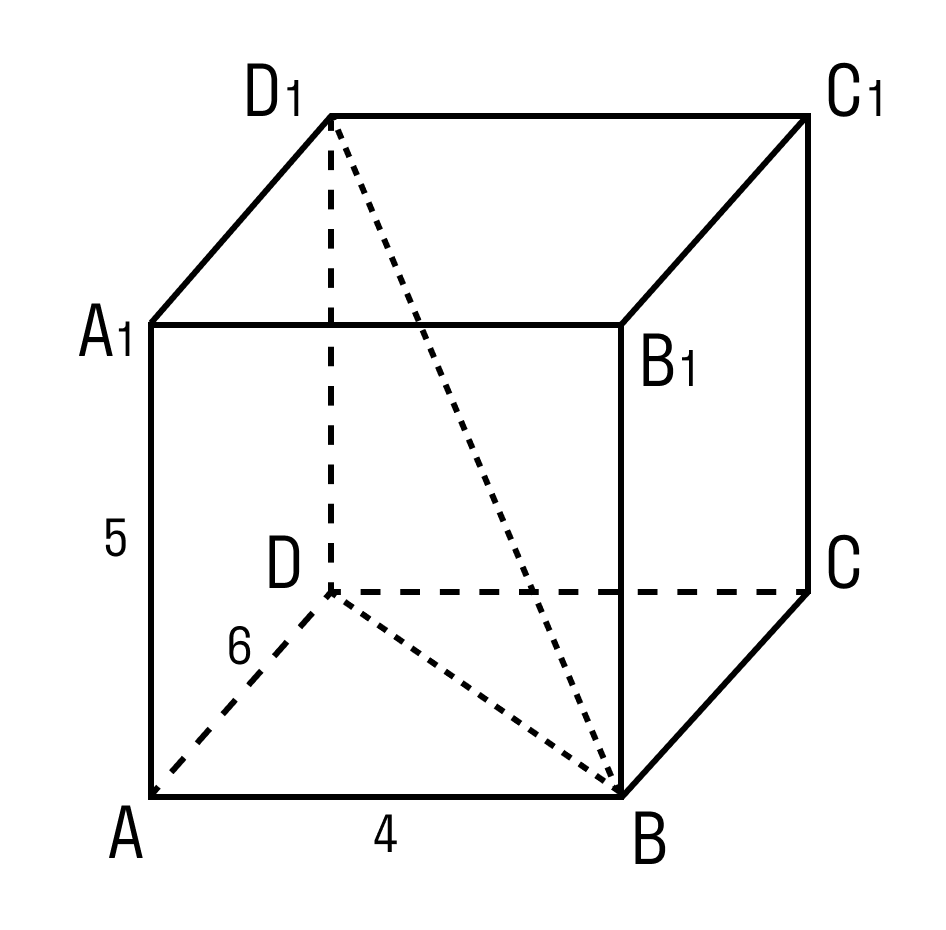
Задачка 3. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

AB = 4
AD = 6
AA₁= 5
Нужно найти отрезок BD₁.

В треугольнике ADB угол A = 90°.

По теореме Пифагора:
BD 2 = AB 2 +AD 2
BD 2 = 4 2 + 6 2 = 16 + 36 = 52
В треугольнике BDD₁ угол D = 90°.
BD₁ 2 = 52 + 25 = 77
BD₁ = √77.

Самопроверка

Теперь потренируйтесь самостоятельно — мы верим, что все получится!

Задачка 1. Дан прямоугольный параллелепипед. Измерения (длина, ширина, высота) = 8, 10, 20. Найдите диагональ параллелепипеда.

Подсказка: если нужно выяснить, чему равна диагональ прямоугольного параллелепипеда, вспоминайте теорему.

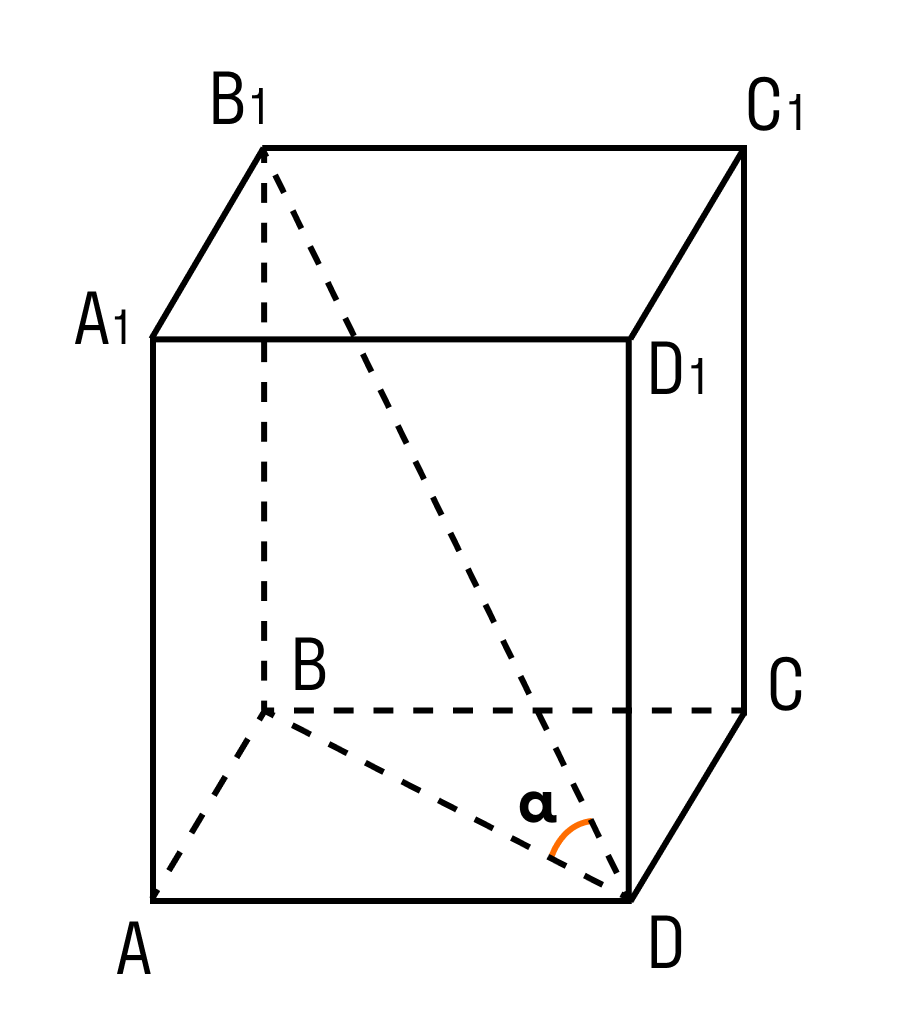
Задачка 2. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

Вычислите длину ребра AA₁.

Как видите, самое страшное в параллелепипеде — 14 букв в названии. Чтобы не перепутать прямой параллелепипед с прямоугольным, а ребро параллелепипеда с длиной диагонали параллелепипеда, вот список основных понятий:

Источник