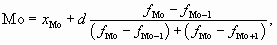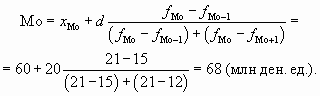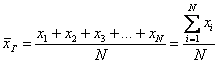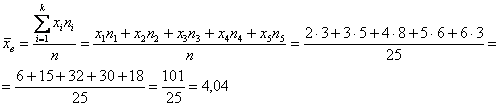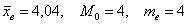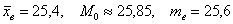Как находить моду в статистике
8.4. МОДА и МЕДИАНА (структурные средние)
Мода и медиана наиболее часто используемые в экономической практике структурные средние.
Мода – это величина признака (варианта), который наиболее часто встречается в данной совокупности, т.e. это варианта, имеющая наибольшую частоту.
В дискретном ряду мода определяется в соответствии с определением, т.е. это одна из вариант признака, которая в ряду распределения имеет наибольшую частоту.
Для интервального ряда моду находим по формуле (8.16), сначала по наибольшей частоте определив модальный интервал:
где х о – начальная (нижняя) граница модального интервала;
h – величина интервала;
fМо – частота модального интервала;
fМо-1 – частота интервала, предшествующая модальному;
fМо+1 – частота интервала следующая за модальным.
Медианой называется такое значение признака, которое приходится на середину ранжированного ряда, т.е. в ранжированном ряду распределения одна половина ряда имеет значение признака больше медианы, другая – меньше медианы.
В дискретном ряду медиана находится непосредственно по накопленной частоте, соответствующей номеру медианы.
В случае интервального вариационного ряда медиану определяют по формуле:

где хо – нижняя граница медианного интервала;
NМе – порядковый номер медианы (Σf/2);
S Me-1 – накопленная частота до медианного интервала;
fМе – частота медианного интервала.
Пример вычисления Моды.
Рассчитаем моду и медиану по данным табл. 8.4.
Таблица 8.4 – Распределение семей города N по размеру среднедушевого дохода в январе 2018 г. руб.(цифры условные)
| Группы семей по размеру дохода, руб. | Число | ||||
| До 5000 | 600 | 600 | 6 | ||
| 5000-6000 | 700 | 1300 (600+700) | 13 | ||
| 6000-7000 | 1700 (fМо-1) | 3000 (S Me-1 ) (хо) | 2500 (fМе) | 5500 (S Me) | 55 |
| 8000-9000 | 2200 (fМо+1) | 7700 | 77 | ||
| 9000-10000 | 1500 | 9200 | 92 | ||
| Свыше 10000 | 800 | 10000 | 100 | ||
| Итого | 10000 | – | – |
Пример вычисления Медианы интервального вариационного ряда. Рассчитаем медиану по формуле (8.17):
1) сначала находим порядковый номер медианы: NМе = Σfi/2= 5000.
2) по накопленным частотам в соответствии с номером медианы определяем, что 5000 находится в интервале (7000 – 8000), далее значение медианы определим по формуле (8.17):
Вывод: по моде – наиболее часто встречается среднедушевой доход в размере 7730 руб., по медиане – что половина семей города имеет среднедушевой доход ниже 7800 руб., остальные семьи – более 7800 руб.
Соотношение моды, медианы и средней арифметической указывает на характер распределения признака в совокупности, позволяет оценить его асимметрию.
Если М о о следует сделать вывод о левосторонней асимметрии ряда.
Определение моды и медианы
По данным таблицы рассчитаем моду и медиану
Диапазон по продолжительности жизни
Число стран (частота), f
Накопленная частота, f
Определение моды
Интервал, имеющий наибольшую частоту, будет являться модальным, а конкретное (дискретное) значение моды будет находиться внутри него. Рассчитать конкретное, значение моды в интервальном ряду можно по следующей формуле:
где: ХМо — нижняя граница модального интервала,
i — длина модального интервала,
fMo — частота модального интервала,
fMo-1 — частота, соответствующая предшествующему интервалу,
fMo+1 — частота, соответствующая последующему интервалу.
Самая большая частота, 37 стран, соответствует варианту 71,70 — 74,43. Этот интервал является модальным.
Определение медианы
Медиана применяется для количественной характеристики структуры и равна такому варианту, который делит ранжированную совокупность на две равные части. У одной половины совокупности признаки не больше медианы (меньше или равны), у второй — не меньше медианы (больше или равны).
Если рассматриваемый ряд интервальный, то накопленные частоты покажут нам медианный интервал. Конкретное значение медианы рассчитывается по формуле:
i — длина медианного интервала,
сумма f — сумма частот ряда (объем совокупности),
f’Me-1 — накопленная частота в интервале, предшествующем медианному,
fMe — частота медианного интервала.
Для нахождения медианного интервала нужно знать половину частот, то есть 150 : 2 = 75. В столбце «накопленные частоты» выбираем 5 интервал, так как в 4 интервале частот накопилось еще 49 стран — меньше половины. С помощью формулы найдем конкретное значение медианы, оно принадлежит медианному интервалу 71,70 — 74,43.
Разница между 74,14 и 73,61 говорит об умеренном асимметричном распределении
Структурные характеристики вариационного ряда распределения
8.1. Мода
8.1.1. Определение моды в дискретных вариационных рядах
В дискретных вариационных рядах для определения моды не требуется специальных вычислений: значение признака, которому соответствует наибольшая частота, и будет значением моды.
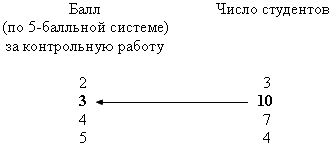
Пример 8.1. По представленным ниже результатам проведения контрольной работы по статистике определим моду.
8.1.2. Определение моды в интервальных вариационных рядах с равными интервалами
Для определения моды в интервальных вариационных рядах с равными интервалами сначала находят модальный интервал, которым является интервал с наибольшей частотой, а затем ведут расчет по формуле
Пример 8.2. Имеются данные по группе банков.
| Сумма выданных кредитов, млн ден. ед. | Количество банков |
|---|---|
| До 40 | 8 |
| 40-60 | 15 |
| 60-80 | 21 |
| 80-100 | 12 |
| 100-120 | 9 |
| 120-140 | 7 |
| 140 и выше | 4 |
| Итого | 77 |
Определим модальный размер выданных кредитов:
Подставив в формулу соответствующие величины, получим
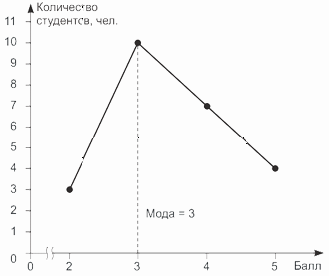
Пример 8.3. По результатам проведения контрольной работы по статистике, приведенным в примере 8.1, определим моду графическим способом.
Для этого построим полигон распределения и найдем абсциссу его вершины (рис. 8.1).
Пример 8.4. По данным о распределении банков по сумме выданных кредитов, приведенным в примере 8.2, определим моду графическим способом (рис. 8.2).
4. Мода. Медиана. Генеральная и выборочная средняя
Мода на экране, медиана в треугольнике, а средние – это температура по больнице и в палате. Продолжаем наш практический курс занимательной статистики (Занятие 1) изучением центральных характеристик статистической совокупности, названия которых вы видите в заголовке. И начнём мы с его конца, поскольку о средних величинах речь зашла практически с первых же абзацев темы. Для подготовленных читателей оглавление:
ну а «чайникам» лучше ознакомиться с материалом по порядку:
Итак, пусть исследуется некоторая генеральная совокупность объёма 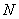
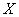
Генеральной средней называется среднее арифметическое всех значений этой совокупности:
Если среди чисел 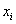
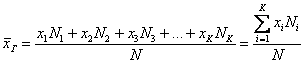
варианта 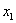
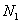
варианта 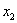
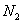
варианта 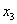
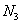
…
варианта 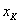
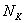
Живой пример вычисления генеральной средней встретился в Примере 2, но чтобы не занудничать, я даже не буду напоминать его содержание.
Далее. Как мы помним, обработка всей генеральной совокупности часто затруднена либо невозможна, и поэтому из неё организуют представительную выборку объема 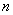
Выборочной средней называется среднее арифметическое всех значений выборки: 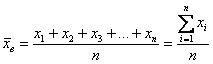
и при наличии одинаковых вариант формула запишется компактнее:
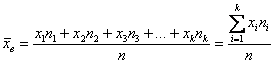
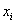
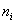
Выборочная средняя 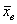
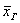
Практику начнём, а точнее продолжим, с дискретного вариационного ряда и знакомого условия:
По результатам выборочного исследования 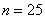
Это числа из Примера 4 (см. по ссылке выше), но теперь нам требуется: вычислить выборочную среднюю, и, не отходя от станка, найти моду и медиану.
Как решать задачу? Если нам даны первичные данные (исходные необработанные значения), то их можно тупо просуммировать и разделить результат на объём выборки:
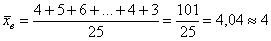
Но во многих задачах требуется составить вариационный ряд (см. Пример 4): 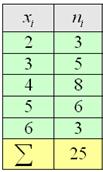
– или же этот ряд предложен изначально (что бывает чаще). И тогда, мы, конечно, используем «цивилизованную» формулу:
Далее. Мода и медиана. Эти понятия тоже вводятся как для генеральной, так и для выборочной совокупности, и определения я сформулирую в общем виде.
Мода. Мода 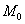
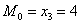
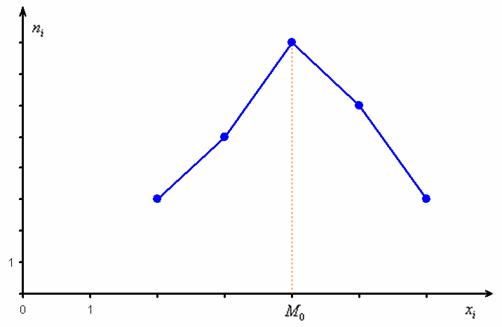
Иногда таковых значений несколько (с одинаковой максимальной частотой), и тогда модой считают каждое из них.
Если все или почти все варианты различны (что характерно для интервального ряда), то модальное значение определяется несколько другим способом, о котором во 2-й части урока.
Медиана. Медиана 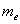
* не важно, дискретного или интервального, генеральной совокупности или выборочной.
Медиану можно отыскать несколькими способами.
Если даны первичные данные, то сортируем их по возрастанию либо убыванию (см. Задание 1) и находим середину ранжированного ряда: 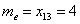
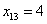
– если совокупность содержит нечётное количество чисел (наш случай), то делим её объём пополам: 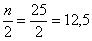
– если совокупность содержит чётное количество чисел, например, 20, то делаем то же самое: 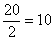
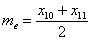
Напоминаю, что изложенная инструкция работает для упорядоченного (по возрастанию либо убыванию) ряда. Но есть и более быстрый путь, где ничего не нужно сортировать. Это использование стандартной функции Экселя:
– забиваем в любую свободную ячейку =МЕДИАНА(, выделяем мышью все числа, закрываем скобку ) и жмём Enter. Попробуйте самостоятельно. Этот способ удобен, когда вам дано много значений.
Следует отметить, что в Экселе существуют и отдельные функции для вычисления средней (=СРЗНАЧ), моды (=МОДА) и ещё много чего, но я против использования этих функций в учебном курсе, за исключением случаев, где это действительно целесообразно. …Почему против? Потому что они не помогают понять суть показателей и, более того, отупляют. Так, среднюю гораздо вразумительнее рассчитывать следующим образом:
=СУММ(выделяем мышью диапазон) / объем совокупности. Вычисления рекомендую опробовать лично (ссылка выше).
Ситуация вторая. Когда составлен либо изначально дан готовый дискретный ряд. Тут можно поступить «по любительски» – начать отсчитывать примерно равное количество чисел по краям ряда: 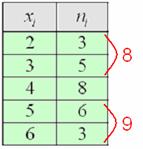
после чего мысленно либо на черновике их отбрасывать, в данном случае отбросим по 8 штук сверху и снизу: 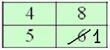
откуда становится ясно, что медианное значение:
Второй способ более академичен, находим относительные накопленные частоты: 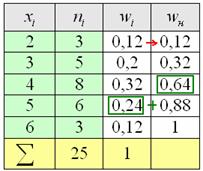
и то значение «икса», у которого 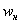
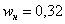
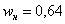
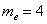
Запишем красивый ответ:
Полученные значения близки друг к другу, и это говорит о симметрии вариационного ряда относительно центра, что хорошо видно по полигону частот (см. чертёж выше). И с высокой вероятностью можно утверждать, что примерно так же распределена и вся генеральная совокупность (все рабочие цеха).
И тут возникает следующий закономерный вопрос: а зачем вообще нужна мода с медианой? – ведь есть средняя.
А дело в том, что в ряде случаев среднее значение неудовлетворительно характеризует центральную тенденцию статистической совокупности:
Известны результаты продаж пиджаков в универмаге города: 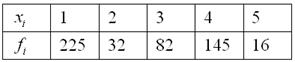
где, 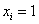
…ну, а если вам не нравятся пиджаки, то представьте какие-нибудь шляпки с цветочками 🙂
Также обратим внимание, что в условии задачи ничего не сказано о том, генеральная ли это совокупность или выборочная, и в подобной ситуации я не рекомендую ничего додумывать – среднюю просто обозначаем через 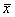
Вычислить среднюю – в экселевском файле уже забиты исходные данные и приведена краткая инструкция. Если под пальцами нет Экселя, то считаем на калькуляторе. Не ленимся! – заданий я предлагаю немного (у вас своих хватает :)), но прорешать их очень важно! Краткое решение для сверки в конце урока.
…какие мысли на счёт полученного значения 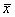
И, конечно, важнейший показатель здесь мода: 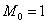
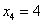
Ещё хуже (в содержательном плане) ситуация с медианой – продолжаем решать задачу в Экселе (ссылка выше) либо в тетради! Особо зоркие читатели медиану углядят и устно, и в конце урока я привёл способ, который просто бросился мне в глаза.
Теперь надеваем пиджаки / шляпы и возвращаемся на фабрику, где бухгалтер Петрова вычислила генеральную среднюю заработную плату рабочих: 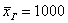
Что будет, если к совокупности добавить руководящий персонал и директора Петрова? Средняя зарплата немного увеличится: 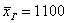
А вот если сюда добавить олигарха Петровского, то полученная средняя 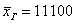
Поэтому, если в статистической совокупности есть «аномальные» отклонения в ту или иную сторону, то в качестве оценки центрального значения как нельзя лучше подходит медиана, которая в нашем условном примере будет равна, скажем, 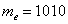
Как вычислить моду, медиану и среднюю интервального ряда?
Начнём опять с ситуации, когда нам даны первичные статические данные:
По результатам выборочного исследования цен на ботинки в магазинах города получены следующие данные (ден. ед.): 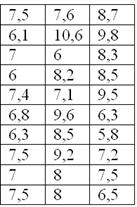
– это в точности числа из Примера 6 статьи об интервальном вариационном ряде.
Но теперь нам нужно найти среднюю, моду и медиану.
Решение: чтобы найти среднюю по первичным данным, нужно просуммировать все варианты и разделить полученный результат на объём совокупности:
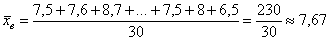
Эти подсчёты, кстати, займут не так много времени и при использовании оффлайн калькулятора. Но если есть Эксель, то, конечно, забиваем в любую свободную ячейку =СУММ(, выделяем мышкой все числа, закрываем скобку ), ставим знак деления /, вводим число 30 и жмём Enter. Готово.
Что касается моды, то её оценка по исходным данным, становится непригодна. Хоть мы и видим среди чисел одинаковые, но среди них запросто может найтись пять так шесть-семь вариант с одинаковой максимальной частотой, например, частотой 2. Кроме того, цены могут быть округлёнными. Поэтому модальное значение рассчитывается по сформированному интервальному ряду (о чём чуть позже).
Чего не скажешь о медиане: забиваем в Эксель =МЕДИАНА(, выделяем мышью все числа, закрываем скобку ) и жмём Enter: 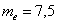
Но в Примере 6 была проведена сортировка по возрастанию (вспоминаем и сортируем – ссылка выше), и это хорошая возможность повторить формальный алгоритм отыскания медианы. Делим объём выборки пополам:
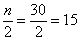
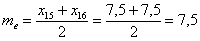
Ситуация вторая. Когда дан готовый интервальный ряд (типичная учебная задача).
Продолжаем анализировать тот же пример с ботинками, где по исходным данным был составлен ИВР. Для вычисления средней потребуются середины 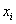
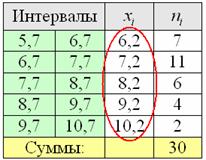
– чтобы воспользоваться знакомой формулой дискретного случая: 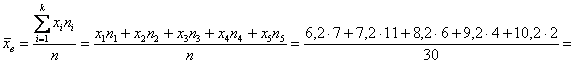
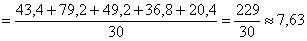
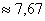
Здесь мы использовали упомянутый ранее приём – приблизили интервальный ряд дискретным, и это приближение оказалось весьма эффективным. Впрочем, особой выгоды тут нет, т.к. при современном программном обеспечении не составляет труда вычислить точное значение даже по очень большому массиву первичных данных. Но это при условии, что они нам известны 😉
С другими центральными показателями всё занятнее.
Чтобы найти моду, нужно найти модальный интервал (с максимальной частотой) – в данной задаче это интервал 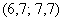
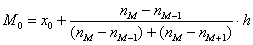
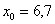
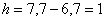
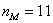
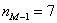
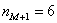
Таким образом:
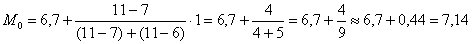
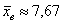
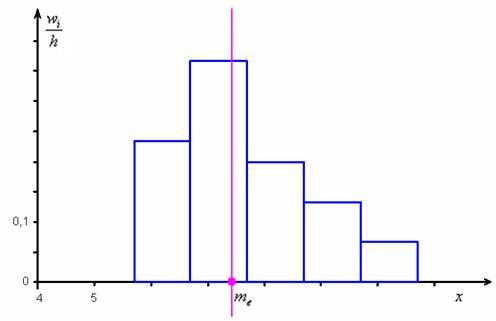
Не вдаваясь в геометрию формулы, просто приведу гистограмму относительных частот и отмечу 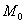
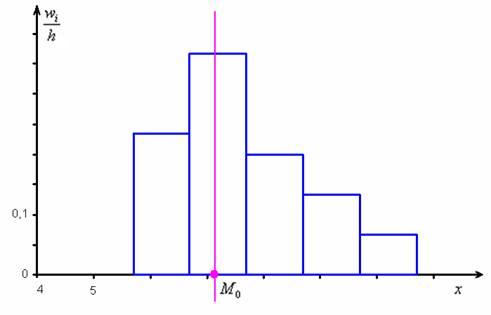
откуда хорошо видно, что мода смещена относительно центра модального интервала в сторону левого интервала с бОльшей частотой. Логично.
Справочно разберу редкие случаи:
– если модальный интервал крайний, то 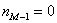
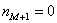
– если обнаружатся 2 модальных интервала, которые находятся рядом, например, 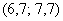
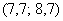
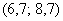
– если между модальными интервалами есть расстояние, то применяем формулу к каждому интервалу, получая тем самым 2 или бОльшее количество мод.
Вот такой вот депеш мод 🙂
И медиана. Если дан готовый интервальный ряд, то медиана рассчитывается чуть по менее страшной формуле, но сначала нудно (описка по Фрейду:)) найти медианный интервал – это интервал, содержащий варианту (либо 2 варианты), которая делит вариационный ряд на две равные части.
Выше я рассказал, как определить медиану, ориентируясь на относительные накопленные частоты 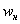
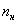
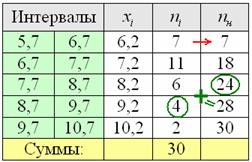
Всем понятен смысл чисел в правом столбце? – это количество вариант, которые успели «накопиться» на всех «пройденных» интервалах, включая текущий.
Поскольку у нас чётное количество вариант (30 штук), то медианным будет тот интервал, который содержит 30/2 = 15-ю и 16-ю варианту. И ориентируясь по накопленным частотам, легко прийти к выводу, что эти варианты содержатся в интервале 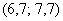
Формула медианы: 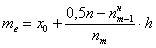
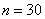
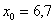
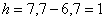
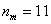
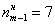
Таким образом:
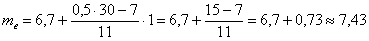
И справочно особые случаи:
– Если медианным является крайний левый интервал, то 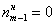
– Если вариационный ряд содержит чётное количество вариант и две средние варианты попали в разные интервалы, то объединяем эти интервалы, и по возможности удваиваем предыдущий интервал
Ответ: 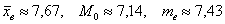
Здесь центральные показатели оказались заметно отличны друг от друга, и это говорит об асимметрии распределения, которая хорошо видна по гистограмме.
И задача для тренировки:
Для изучения затрат времени на изготовление одной детали рабочими завода проведена выборка, в результате которой получено следующее статистическое распределение: 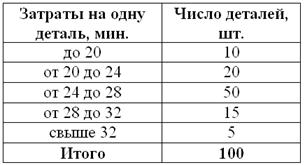
…да, тематичная у меня получилась статья 🙂
Найти среднюю, моду и медиану.
Это, кстати, уже каноничная «интервальная» задача, в которой исследуется непрерывная величина – время.
Решаем эту задачу в Экселе – все числа и инструкции уже там. Если нет Экселя, считаем на калькуляторе, что в данном случае может оказаться даже удобнее. Образец решения, как обычно, в конце урока.
Несмотря на разнообразия рассмотренных показателей, их всё равно бывает не достаточно. Существуют крайне неоднородные совокупности, у которых варианты «кучкуются» во многих местах, и по этой причине средняя, мода и медиана неудовлетворительно характеризуют центральную тенденцию.
В таких случаях вариационный ряд дробят с помощью квартилей, децилей, а в упоротых специализированных исследованиях – и с помощью перцентилей.
Квартили упорядоченного вариационного ряда – это варианты 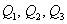
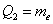
В тяжёлых случаях проводится разбиение на 10 частей – децилями 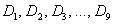
И в очень тяжелых случаях в ход пускается 99 перцентилей 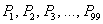
И после разбиения вариационного ряда каждый участок исследуется по отдельности – рассчитываются локальные средние показатели, локальные показатели вариации и т.д.
В учебном курсе квартили, децили, перцентили встречаются редко, и посему я оставляю этот материал (их нахождение) для самостоятельного изучения.
Ну а сейчас мы перейдём к рассмотрению другой группы статистических показателей – как раз к показателям вариации.
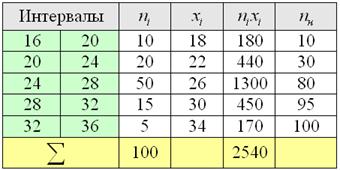
Пример 9. Решение: заполним расчётную таблицу: 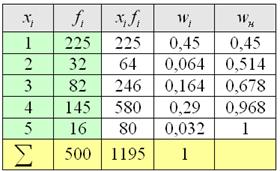
Вычислим среднюю:
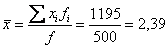
По правому столбцу определяем «иксовое» значение, которое делит совокупность на 2 равные части: 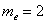
Кроме того, медиану легко усмотреть и устно – поскольку половина совокупности равна 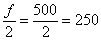
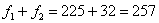
Пример 11. Решение: поскольку длина внутренних интервалов равна 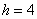
Вычислим выборочную среднюю:
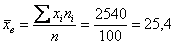
Моду вычислим по формуле 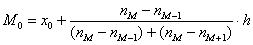
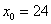
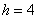
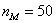
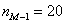
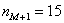
Таким образом:
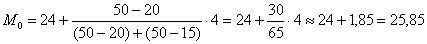
Анализируя накопленные частоты, приходим к выводу, что медианным является интервал 
Медиану вычислим по формуле 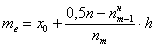
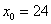
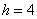
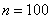
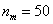
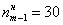
Таким образом:
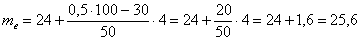
Ответ: среднее время изготовления детали характеризуется следующими центральными характеристиками:
Автор: Емелин Александр
(Переход на главную страницу)

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5