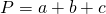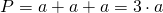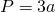Как находить периметр равностороннего треугольника
Как найти периметр треугольника
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение
Периметром принято называть длину всех сторон многоугольника. Периметр обозначается заглавной латинской буквой P. Под «P» удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах и ходе решении.
Важно, чтобы все параметры были переданы в одной единице длины, иначе мы не сможем подсчитать результат. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.
В чем измеряется периметр:
Как узнать периметр треугольника
Рассмотрим какие существуют формулы, и при каких известных исходных данных их можно применять.
Если известны три стороны, то периметр треугольника равен их сумме. Этот способ проходят во втором классе.
P = a + b + c, где a, b, c — длина стороны.
Если известна площадь и радиус вписанной окружности:
P = 2 * S : r, где S — площадь, r — радиус вписанной окружности.
Если известны две стороны и угол между ними, вычислить периметр треугольника можно так:
Если известна одна сторона в равностороннем треугольнике:
P = 3 * a, где a — длина стороны.
Все стороны в равносторонней фигуре равны.
Если известна боковая сторона и основание в равнобедренном треугольнике:
P = 2 * a + b, где a — боковая сторона, b — основание.
Боковые стороны в равнобедренной фигуре равны.
Если известна боковая сторона и высота в равнобедренном треугольнике:
P = 2 * (√ a 2 + h 2 ) + 2 * a, где a — боковая сторона, h — высота.
Высотой принято называть отрезок, который вышел из вершины и опустился на основание. В равнобедренной фигуре высота делит основание пополам.
Если известны катеты в прямоугольном треугольнике:
P = √ a 2 + b 2 + (a + b), где a, b — катеты.
Катет — одна из двух сторон, которые образуют прямой угол.
Если известны катет и гипотенуза в прямоугольном треугольнике:
Гипотенуза — сторона, которая лежит напротив прямого угла.
Скачать онлайн таблицу
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.
Периметр равностороннего треугольника

Всего получено оценок: 306.
Всего получено оценок: 306.
Равносторонний треугольник занимает особое место среди треугольников. Для того, чтобы найти значение периметра, площади, углов или радиусов окружностей вписанной и описанной у равнобедренного треугольника, достаточно знать величину стороны. С одной стороны, это значительно облегчает решение, с другой составители задач редко дают значение стороны и приходится искать обходные пути решения.
Формула нахождения периметра равностороннего треугольника
Формула периметра равностороннего треугольника вытекает из определений. Что такое периметр? Периметр это сумма всех сторон фигуры. Равносторонний треугольник – это треугольник, все стороны которого равны.
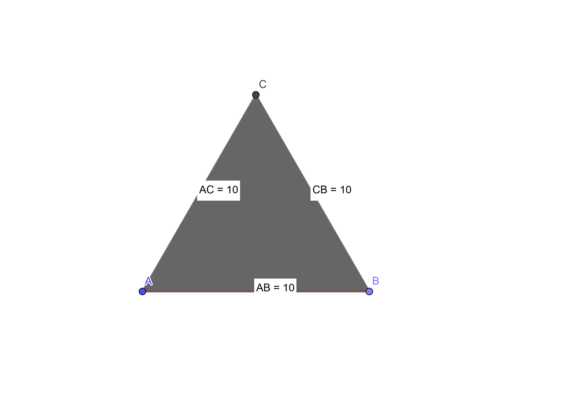
Значит,для того, чтобы найти значение периметра достаточно умножить величину стороны на количество сторон:
Решим несколько разных по сложности задач, чтобы разобраться, какие проблемы могут встречаться на пути нахождения периметра.
Задача 1
Это самый простой вариант задачи. Достаточно подставить значение в формулу и получить результат. Такая задача не должна вызывать затруднений:
Задача 2
Особое внимание нужно обращать на вид фигуры, который указан в условии задачи.
В данной задаче дан равнобедренный треугольник. Чтобы воспользоваться общей формулой, необходимо доказать, что этот равнобедренный треугольник является еще и равносторонним.
Обратим внимание на величину угла. Угол при основании равен 60. При этом углы у основания равнобедренного треугольника равны, а сумма углов любого треугольника равна 180 градусов. Значит у основания два угла по 60 градусов. Рассчитаем угол при вершине:
180-60-60=60 – угол при вершине так же равен 60 градусам.
Значит, данный треугольник будет равносторонним, так как все углы равны 60 градусам.
Углы по 60 градусов характерны только для равностороннего треугольника. Именно сочетание 3 равных сторон образует 3 равных угла. В любых других ситуациях, хотя бы один угол будет отличаться.
Для площади равностороннего треугольника имеется отдельная формула:
$$S=a^2*<\sqrt<3>\over 4>=<64\over\sqrt<3>>$$ – где а значение стороны, которое нам и нужно выразить из этой формулы.
Подставим полученное значение в формулу:
Задача 3
Для данной задачи нужно воспользоваться методом решения, который часто используется в задачах с равнобедренным треугольником. Из любой вершины опустим высоту, которая будет медианой и биссектрисой.
В одном из получившихся треугольников выразим значение высоты через сторону с помощью теоремы Пифагора:
Вычтем подобные слагаемые:
Из получившейся формулы выразим значение стороны:
Подставим получившееся значение в формулу периметра равностороннего треугольника.
Что мы узнали?
Мы обсудили формулу для нахождения периметра равностороннего треугольника. Выделили проблемы, которые приходится решать при нахождении стороны равностороннего треугольника для дальнейшего решения задачи. Рассмотрели различные пути решения задач на нахождение периметра равностороннего треугольника.
Периметр равностороннего треугольника
Чтобы найти периметр равностороннего треугольника(или найти периметр правильного треугольника), нужно знать его сторону.
В общем случае для нахождения периметра треугольника используют формулу
Поскольку в равностороннем треугольнике все три стороны равны, формула упрощается:
Таким образом, формула периметра равностороннего треугольника:
(а — длина его стороны).
1) Найти периметр равностороннего треугольника, сторона которого равна 10 см.
По формуле Р=3а имеем: Р=3∙10=30 (см).
2) Периметр равностороннего треугольника равен 21 см. Найти его сторону.
Р=3а, значит, а=Р:3. Таким образом, длина стороны треугольника равна а=21:3= 7 (см).

Периметр равностороннего треугольника — формула и примеры нахождения
В задачах по математике иногда приходится находить суммарное значение всех сторон равностороннего треугольника, формула периметра которого немного отличается от других фигур. Чтобы разбираться в материале, нужно ознакомиться с формулировками основных определений, а также доказать теорему практическим путем.
Общие сведения
Изучение любой фигуры, процесса или явления всегда начинается с определений. Треугольником называется геометрическое тело, состоящее из трех, не лежащих на одной прямой, вершин. Прямая — совокупность бесконечного количества точек, лежащих в одной плоскости и проходящих без искажений.
Вершина — точка, образованная сторонами треугольника. Периметр — суммарное значение всех сторон любой фигуры. Высота — отрезок, проведенный из любой вершины на сторону, которая является противоположной, под углом в 90 градусов.
Медиана — часть прямой, проведенной из вершины, но не под прямым углом, а соединяющая ее с серединой противолежащей стороны. Биссектриса — прямая, делящая угол на 2 равных величины.
Виды треугольников
Треугольники классифицируются по углам и сторонам. На основании первого критерия можно выделить несколько типов фигур:
В первом случае у фигуры все углы острые, т. е. градусная мера каждого не должна превышать 90 градусов. Если хотя бы один из них эквивалентен 90, треугольник является прямоугольным. Однако когда градусная мера одного из них превышает 90, он принадлежит к третьему типу.
Треугольники классифицируются еще и по сторонам. Распределение на группы происходит по такому принципу:
Равнобедренный треугольник можно считать прямоугольным и тупоугольным. Кроме того, равносторонняя фигура всегда является остроугольной. Далее необходимо перейти к доказательству теоремы о периметре.
Теорема о периметре
Каждому ученику известна формула периметра треугольника для 3 класса. Она является довольно примитивным соотношением, и применяется в абсолютно другом виде в старших классах и высших учебных заведениях. Математики предлагают рассмотреть доказательство теоремы о периметре правильного треугольника. Ее формулировка имеет следующий вид: периметр треугольника равен утроенному произведению одной из его сторон, когда фигура является правильной.
Доказывается утверждение очень просто. Для этого необходимо использовать следующий алгоритм:
Можно найти и другое доказательство теоремы, в которой используется прямоугольник. В фигуре нужно провести диагонали, а затем по формуле Пифагора выразить боковые стороны. Однако процесс доказательства утверждения является более сложным.
У каждой теоремы есть какие-либо следствия. Они позволяют существенно оптимизировать вычисления при решении задач. Далее необходимо рассмотреть полезные формулы.
Полезные формулы
Для вычисления различных параметров треугольника применяются определенные формулы. Кроме того, вводится новая величина, которая называется полупериметром. Она обозначается литерой «р» и составляет половину от периметра, т. е. р=Р/2. Специалисты рекомендуют использовать следующие формулы (если известны исходные параметры):
Последнее соотношение редко применяется при решении задач. Однако при известных величинах площади и одной из сторон правильного треугольника значения можно подставить сразу в формулу, а не тратить время на вычисление высоты.
Пример решения задачи
Для закрепления теоретического материала нужно решить задачу по геометрии. Ее условие имеет следующий вид:
В задаче нужно найти значение стороны. Чтобы выполнить эту операцию, необходимо составить 2 уравнения. Однако для начала требуется обозначить неизвестную величину переменной «t». В результате получается следующая система алгебраических выражений с неизвестными:
Чтобы вычислить величину переменной, необходимо выразить ее в первом тождестве, т. е. t=S-8. После этого нужно подставить все известные значения: t=12*(3)^(½) — 8 = 4*(3)^(½). Для проверки правильности решения нужно воспользоваться вторым соотношением, которое позволит вычислять площадь: 4*(3)^(½) * 3 = 12*(3)^(½).
Из последнего расчета можно сделать вывод, что сторона треугольника определена правильно и равна 4*(3)^(½). Значение периметра в этом случае будет равно 12*(3)^(½) сантиметров.
Таким образом, для решения задач по геометрии необходимо знать теорему о периметре и формулы для расчетов различных параметров равностороннего треугольника.
Периметр и площадь треугольника
Периметр
Периметр любого треугольника равен сумме длин трёх его сторон. Общая формула для нахождения периметра треугольников:
где P — это периметр треугольника, a, b и c — его стороны.
Периметр равнобедренного треугольника можно найти сложив последовательно длины его сторон или умножив длину боковой стороны на 2 и прибавив к произведению длину основания. Общая формула для нахождения периметра равнобедренных треугольников будет выглядеть так:
где P — это периметр равнобедренного треугольника, a — любая из боковых сторон, b — основание.
Периметр равностороннего треугольника можно найти сложив последовательно длины его сторон или умножив длину любой его стороны на 3. Общая формула для нахождения периметра равносторонних треугольников будет выглядеть так:
где P — это периметр равностороннего треугольника, a — любая из его сторон.
Площадь
Для измерения площади треугольника можно сравнить его с параллелограммом. Рассмотрим треугольник ABC:
Если взять равный ему треугольник и приставить его так, чтобы получился параллелограмм, то получится параллелограмм с той же высотой и основанием, что и у данного треугольника:
В данном случае общая сторона сложенных вместе треугольников является диагональю образованного параллелограмма. Из свойства параллелограммов известно, что диагональ всегда делит параллелограмм на два равных треугольника, значит площадь каждого треугольника равна половине площади параллелограмма.
Так как площадь параллелограмма равна произведению его основания на высоту, то площадь треугольника будет равна половине этого произведения. Значит для ΔABC площадь будет равна
Теперь рассмотрим прямоугольный треугольник:
Два равных прямоугольных треугольника можно сложить в прямоугольник, если прислонить их друг к другу гипотенузой. Так как площадь прямоугольника равна произведению его смежных сторон, то площадь данного треугольника равна:
Из это можно сделать вывод, что площадь любого прямоугольного треугольника равна произведению катетов, разделённому на 2.
Из данных примеров можно сделать вывод, что площадь любого треугольника равна произведению длин основания и высоты, опущенной на основание, разделённому на 2.
Общая формула площади треугольника:
где S — это площадь треугольника, a — его основание, ha — высота, опущенная на основание a.