Как находить площадь параллелограмма 9 класс

Нахождение площади параллелограмма: формула и примеры

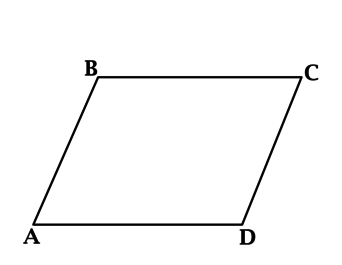
Параллелограмм – это геометрическая фигура; четырехугольник, у которого противоположные стороны равны и параллельны.

Формула вычисления площади

По длине стороны и высоте

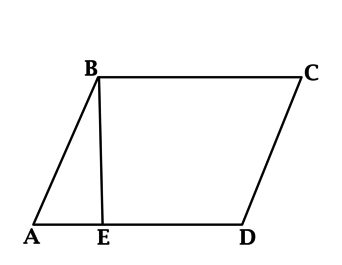
Площадь параллелограмма (S) равняется произведению длины его стороны и высоты, проведенной к ней:

S = a ⋅ h

По двум сторонам и углу между ними

Площадь параллелограмма находится путем умножения длин его обеих сторон и синуса угла между ними:

S = a ⋅ b ⋅ sin α

По двум диагоналям и углу между ними

Площадь параллелограмма равна одной второй произведения длин его диагоналей, умноженного на синус угла между ними:

Примеры задач

Задание 1
Найдите площадь параллелограмма, если длина его стороны равняется 7 см, а высоты – 4 см.

Задание 2
Найдите площадь параллелограмма, если его стороны равны 6 и 8 см, а угол между ними – 30°.

Задание 3
Найдите площадь параллелограмма с диагоналями, равными 4 и 6 см. Угол между ними составляет 90°.

Источник

Площади фигур. Площадь параллелограмма.

Площадь плоской фигуры — аддитивная числовая характеристика фигуры, полностью принадлежащей

одной плоскости. Если фигуру можно разбить на конечное множество единичных квадратов, то площадь

будет равна числу этих квадратов.

Параллелограмм это четырехугольник, у которого противоположные стороны попарно параллельны и

лежат на параллельных прямых.

Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус

Воспользуйтесь нашим калькулятором для расчета площади параллелограмма.

Для расчета площади других фигур воспользуйтесь этим калькулятором: площади фигур.

Формулы для определения площади параллелограмма:

1. Площадь параллелограмма по длине стороны и высоте.

Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону

2. Площадь параллелограмма по двум сторонам и углу между ними.

Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.

3. Площадь параллелограмма по двум диагоналям и углу между ними.

d₁, d₂ — длины диагоналей параллелограмма,

Источник

Параллелограмм и его свойства

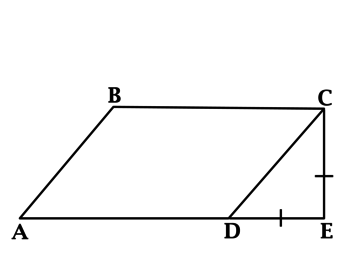
Свойства параллелограмма:

\(\blacktriangleright\) Противоположные стороны попарно равны;

\(\blacktriangleright\) Диагонали точкой пересечения делятся пополам;

Признаки параллелограмма.
Если для выпуклого четырехугольника выполнено одно из следующих условий, то это – параллелограмм:

\(\blacktriangleright\) если противоположные стороны попарно равны;

\(\blacktriangleright\) если две стороны равны и параллельны;

\(\blacktriangleright\) если диагонали точкой пересечения делятся пополам;

\(\blacktriangleright\) если противоположные углы попарно равны.

Площадь параллелограмма

Площадь параллелограмма равна произведению высоты на основание, к которому проведена эта высота.

Задачи из раздела «Геометрия на плоскости» являются обязательной частью аттестационного экзамена у выпускников средней школы. Теме «Параллелограмм и его свойства» в ЕГЭ традиционно отводится сразу несколько заданий. Они могут требовать от школьника как краткого, так и развернутого ответа с построением чертежа. Поэтому если одним из ваших слабых мест являются именно задачи на вычисление площадей параллелограмма или его сторон и углов, то вам непременно стоит повторить или вновь разобраться в материале.

Сделать это легко и эффективно вам поможет образовательный портал «Школково». Наши опытные специалисты подготовили необходимый теоретический материал, изложив его таким образом, чтобы школьники с любым уровнем подготовки смогли восполнить пробелы в знаниях и легко решить задачи ЕГЭ на вычисление площадей, сторон, углов или свойства биссектрисы параллелограмма. Найти базовую информацию вы можете в разделе «Теоретическая справка».

Чтобы успешно решить задачи ЕГЭ по теме «Параллелограмм и его свойства», предлагаем попрактиковаться в выполнении соответствующих упражнений. Большая подборка заданий представлена в блоке «Каталог». Специалисты портала «Школково» регулярно дополняют и обновляют данный раздел.

Последовательно выполнять упражнения учащиеся из Москвы и других городов могут в режиме онлайн. При необходимости любое задание можно сохранить в разделе «Избранное» и в дальнейшем вернуться к нему, чтобы обсудить с преподавателем.

Источник