Как находить площадь поверхности прямоугольного параллелепипеда
Площадь параллелепипеда
Найти площадь параллелепипеда, зная ребра
Формула нахождения полной площади параллелепипеда
Параллелепипед – это четырехугольная призма, в основании имеющая параллелограмм. Существуют готовые формулы для расчета боковой и полной площади поверхности фигуры, для которых необходимы лишь длины трех измерений параллелепипеда.
Общие понятия
Изучим основные понятия. В дальнейших наших рассуждениях площадь будем обозначать латинской буквой S, угол между сторонами a и b будем обозначать как (ab).
Параллелепипедом в математике именуется четырехугольная призма, у которой все грани являются параллелограммами.
Площадь поверхности куба
Здесь все крайне просто — грани этой фигуры равны между собой, так что S = a*a*6.
На примере это выглядит следующим образом:
Сторона равна 88 сантиметров. Площадь полной поверхности?
При данных условиях имеем:
S = a*a*6 = 88*88*6 = 46 464 сантиметра квадратного.
Пример задачи
Вычислите площадь поверхности прямоугольного параллелепипеда, если известно, что его длина равна 6 см, ширина – 4 см, а высота – 7 см.
Нахождение площадей фигур
Рассмотрим, как находятся площади, могущие составлять грани параллелепипеда.
Рассмотрим на примерах как найти площадь каждой из рассматриваемых нами фигур.
1. Длина стороны квадрата равна 1600 метров. Определим его площадь.
2. Стороны прямоугольника равны 90 и 200 метров соответственно. Определим его S.
3. С параллелограммом рассмотрим два случая нахождения.
Сторона равна 300 метров, а опущенная на неё высота 250 метров. Тогда получится:
Второй вариант — стороны равны 550 и 200 метров соответственно. Угол между ними 30 градусов. Имеем:
Как видно из примеров, приведённых выше, никаких сложностей нет.
Как найти площадь боковой поверхности прямоугольного параллелепипеда
Необходимо различать прямоугольный и прямой параллелепипед. Основание прямой фигуры может представлять собой любой параллелограмм. Площадь такой фигуры необходимо вычислять по другим формулам.
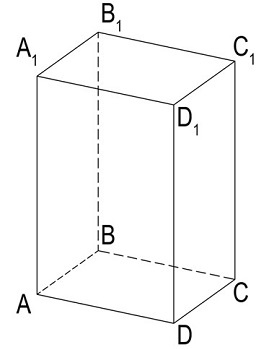
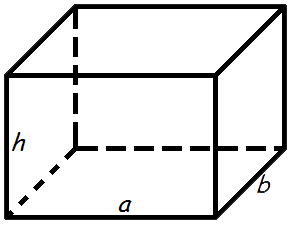
Сумма S боковых граней прямоугольного параллелепипеда вычисляется по простой формуле P*h, где P – периметр и h – высота. На рисунке видно, что у прямоугольного параллелепипеда противоположные грани равны, а высота h совпадает с длиной ребер, перпендикулярных основанию.
Найти площадь поверхности параллелепипеда
Параллелепипед – это призма, основанием которой служит параллелограмм. В параллелепипеде противоположные грани равны и параллельны. Диагонали его пересекаются в одной точке, которая лежит на оси симметрий, и делятся ею пополам.
Площадь полной поверхности параллелепипеда равна сумме площадей её боковых поверхностей и площади основания:
S = 2 cdot (a cdot b + b cdot c + a cdot c)
Дано:
Решение:
По формуле площади поверхности прямоугольного параллелепипеда:
S = 2 cdot ( a cdot b + a cdot c + b cdot c)
S = 2 cdot ( 2 cdot 3 + 2 cdot 4 + 3 cdot 4) = 52 см^2
Ответ:
Дано:
Решение:
S = 2 cdot (a cdot b + a cdot c + b cdot c)
S = 2 cdot (3 cdot 6 + 3 cdot 5 + 5 cdot 6)
Ответ:
Дано:
Решение:
По формуле площади поверхности прямоугольного параллелепипеда находим площадь:
S = 2 cdot (a cdot b + a cdot c + b cdot c)
S = 2 cdot (1 cdot 2 + 1 cdot 3 + 2 cdot 3) = 22 см^2
Ответ:
Дано:
Решение:
S = 2 cdot (a cdot b + a cdot c + b cdot c)
S = 2 cdot (2 cdot 2 + 2 cdot 5 + 2 cdot 5) = 48 см^2
Ответ:
Дано:
Решение:
По формуле для площади поверхности прямоугольного параллелепипеда находим площадь:
S = 2 cdot (a cdot b + a cdot c + b cdot c)
S = 2 cdot (2 cdot 4 + 2 cdot 4 + 4 cdot 4) = 64 см^2
Ответ S = 64 см^2
Пример решения задачи
Приведенные формулы могут использоваться в ходе поиска диагоналей параллелепипеда.
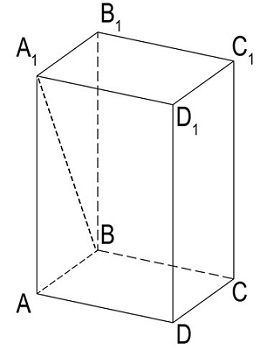
Для нахождение B1D достаточно применить теорему Пифагора: сумма квадратов катетов равна квадрату гипотенузы.
Формула вычисления площади
Площадь (S) поверхности прямоугольного параллелепипеда вычисляется следующим образом:
Формула получена следующим образом:
Заключение
Тщательно изучив все сказанное выше, можно отметить, что никакой особой сложности задача по определению площади параллелепипеда не вызывает. Нужно всего-навсего чётко представлять все данные в материале математические понятия, абсолютно точно выучить формулы, ну и, разумеется, уметь хорошо проводить арифметические действия.
Площадь поверхности параллелепипеда
Что такое площадь поверхности параллелепипеда
Параллелепипед — четырехугольная призма, основаниями которой являются параллелограммы. Частный случай этой геометрической фигуры — прямой параллелепипед, у которого все грани являются прямоугольниками.
В общем случае площадь — это численное значение, характеризующее размер двумерной геометрической фигуры.
Параллелепипед может существовать только в трех измерениях, поэтому для него вводится понятие площади поверхности. В геометрическом смысле площадь поверхности объемной фигуры является совокупностью площадей ее граней.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Формула нахождения полной площади
В задачах чаще всего имеется дело с прямоугольным параллелепипедом. Для него полная площадь поверхности вычисляется следующим образом:
\(S=2\cdot(a\cdot b+a\cdot c+b\cdot c)\)
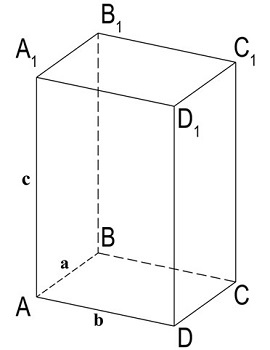
где a, b и c — длины ребер, исходящих из любой вершины параллелепипеда.
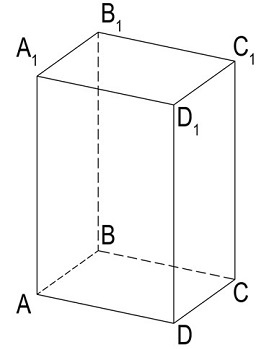
Рассмотрим то, как данная формула выводится. Как уже упоминалось выше, площадь поверхности объемной фигуры является совокупностью площадей ее граней. Для наглядности возьмем параллелепипед ABCDA1B1C1D1.
Полная площадь его поверхности равняется сумме площадей всех граней: \(S_<пар>=S_
Согласно свойствам параллелепипеда, его противоположные грани равны между собой. Следовательно, нет необходимости вычислять площадь всех шести граней, можно ограничиться тремя, а затем их сумму умножить на 2:
Грани прямого параллелепипеда являются прямоугольниками. Площадь данной фигуры равняется произведению ее сторон:
У выбранных нами для расчета площади граней есть три общие стороны: AB, AD и AA1. Для удобства обозначим их как a, b и c соответственно.
Подставим данные значения в обозначенную выше формулу площади параллелепипеда:
\(S_<пар>=2\cdot\left(a\cdot b+a\cdot c+b\cdot c\right)\)
Вычисление площади боковой поверхности прямоугольного параллелепипеда
Кроме полной площади поверхности, в расчетах иногда необходимо вычислить площадь боковой поверхности, то есть совокупность площадей боковых граней, без учета оснований.
Для этого есть три взаимосвязанные формулы:
Примеры решения задач
Задача
Вычислить полную площадь поверхности прямоугольного параллелепипеда ABCDA1B1C1D1.
Дано: AB = 3, A1B = 6, AD = 5.
Решение
Для расчета полной площади необходимо знать длины трех сторон. В данном случае нам понадобится вычислить длину стороны AA1. Так как длина диагонали A1B известна, сделать это нетрудно.
Воспользуемся теоремой Пифагора:
Подставим известные значения в формулу расчета площади поверхности:
\(S=2\cdot(a\cdot b+a\cdot c+b\cdot c)\)
\(S=2\cdot(AB\cdot AD+AB\cdot AA_1+AD\cdot AA_1)=2\cdot(3\cdot5+3\cdot5+5\cdot5)=2\cdot(15+15+25)=2\cdot55=110\)
Задача 2
Вычислить длину стороны прямого параллелепипеда ABCDA1B1C1D1.
Решение
Так как нам известна одна из сторон основания — b а в основании параллелепипеда лежит прямоугольник, найти вторую сторону проще всего будет через площадь этого основания:
Отличие площади боковой поверхности от полной в том, что в ней не учитываются нижняя и верхняя грани фигуры. Следовательно, их разность будет равняться двум площадям основания. Вычислим это значение:
\(S_<пов>-S_<бок>=2\cdot a\cdot b+2\cdot a\cdot c+2\cdot b\cdot c-2\cdot a\cdot c-2\cdot b\cdot c=2\cdot a\cdot b\)
Преобразуем выражение так, чтобы вычислить длину неизвестной стороны:
Онлайн калькулятор. Площадь прямоугольного параллелепипеда
Используя этот онлайн калькулятор, вы сможете найти площадь поверхности прямоугольного параллелепипеда.
Воспользовавшись онлайн калькулятором для вычисления площади поверхности прямоугольного параллелепипеда, вы получите детальное пошаговое решение вашего примера, которое позволит понять алгоритм решения таких задач и закрепить пройденный материал.
Найти площадь поверхности прямоугольного параллелепипеда
| a = |
| b = |
| h = |
Ввод данных в калькулятор для вычисления площади прямоугольного параллелепипеда
В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.
N.B. В онлайн калькуляте можно использовать величины в однаквых единицах измерения!
Если у вас возниели трудности с преобразованием единиц измерения воспользуйтесь конвертером единиц расстояния и длины и конвертером единиц площади.
Дополнительные возможности калькулятора вычисления площади прямоугольного параллелепипеда
Теория. Площадь поверхности прямоугольного параллелепипеда
Формула для вычисления площади прямоугольного параллелепипеда
S = 2( a · b + a · h + b · h )
Все тонкости того, как вычислить площадь параллелепипеда
Что он собой представляет?
Это призма с четырехугольным основанием. Поэтому у нее четыре боковых грани, которые являются параллелограммами. То есть такое тело имеет всего 6 граней.
Для определения параллелепипеда в пространстве у него определяют площадь и объем. Первая может быть как отдельно для каждой грани, так и для всей поверхности. К тому же выделяют еще и площадь только боковых граней.
Какие существуют виды параллелепипедов?
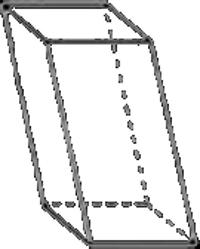
Наклонный. Такой, у которого боковые грани образуют с основанием угол, отличный от 90 градусов. У него верхний и нижний четырехугольники не лежат друг напротив друга, а сдвинуты.
Прямой. Параллелепипед, боковые грани которого являются прямоугольниками, а в основании лежит фигура с произвольными величинами углов.
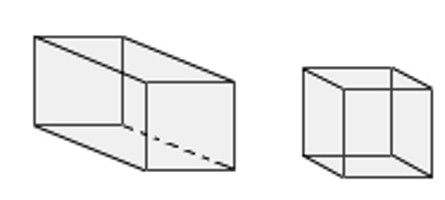
Прямоугольный. Частный случай предыдущего вида: в его основании находится прямоугольник.
Куб. Особый тип прямого параллелепипеда, в котором все грани представлены квадратами.
Некоторые математические особенности параллелепипеда
Может возникнуть ситуация, когда они окажутся полезными в том, чтобы найти площадь параллелепипеда.
Площади прямого параллелепипеда
Если обозначить высоту тела как «н», а периметр основания буквой Рос, то вся боковая поверхность может быть вычислена по формуле:
Используя эту формулу и определив площадь основания, можно сосчитать полную площадь:
В последней записи Sос., то есть площадь основания параллелепипеда, может быть вычислена по формуле для параллелограмма. Другими словами, потребуется выражение, в котором нужно перемножить сторону и высоту, опущенную на нее.
Площади прямоугольного параллелепипеда
Принято стандартное обозначение длины, ширины и высоты такого тела буквами «а», «в» и «с» соответственно. Площадь боковой поверхности будет выражаться формулой:
Чтобы вычислить полную площадь прямоугольного параллелепипеда, потребуется такое выражение:
Если окажется необходимым узнать площадь его основания, то достаточно вспомнить, что это прямоугольник, а значит, достаточно перемножить «а» и «в».
Площади куба
Его боковая поверхность образована четырьмя квадратами. Значит, чтобы ее найти, потребуется воспользоваться известной для квадрата формулой и умножить ее на четыре.
Sбок = 4 * а 2
S = 6 * а 2
Площади наклонного параллелепипеда
Задачи по теме
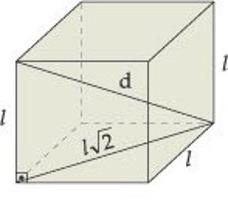
Решение. Начать нужно с получения выражения для искомой величины. Ее квадрат равен трем квадратам стороны куба. Это значит, что диагональ равна «а», умноженной на корень из 3.
Но сторона куба неизвестна. Здесь потребуется воспользоваться тем, что известна площадь всей поверхности. Из формулы получается, что «а» равно квадратному корню из частного S и 6.
Осталось только сосчитать. Ребро куба оказывается равным √ (200/6), что равно 10/ √3 (мм). Тогда диагональ получится равной (10/ √3) * √3 = 10 (мм).
Ответ. Диагональ куба равна 10 мм.
Решение. Потребуется воспользоваться той же формулой для площади куба. В ней опять неизвестно ребро тела. Но зато дан объем. Из формулы для куба очень просто узнать «а». Оно будет равно кубическому корню из 343. Простой подсчет дает такое значение для ребра: а = 7 см.
Теперь осталось только сосчитать его квадрат и умножить на 6. а 2 = 7 2 = 49, отсюда площадь окажется равной 49 * 6 = 294 (см 2 ).
Решение. Начинать рассуждения нужно с формулы для площади всей поверхности тела. Только в ней нужно учесть, что ребра «а» и «в» равны. Это следует из утверждения о том, что призма правильная. Значит, в его основании лежит четырехугольник с равными сторонами. Отсюда а = в = 20 дм.
Учитывая это обстоятельство, формула площади упростится до такой:
В ней известно все, кроме искомой величины «с», которая как раз и является боковым ребром параллелепипеда. Чтобы его найти, нужно выполнить преобразования:
В итоге получится выражение:
После подстановки всех известных величин и выполнения действий получается, что боковое ребро равно 12 дм.
Ответ. Боковое ребро «с» равняется 12 дм.
Теперь нужно воспользоваться известным объемом. Его формула для прямоугольного параллелепипеда дает произведение всех трех величин: «а», «в» и «с». То есть известная площадь, умноженная на «в», дает объем. Отсюда получается, что искомое ребро можно вычислить из уравнения:
Элементарный расчет дает результат 5.
Ответ. Искомое ребро равно 5 см.
Задание пятое. Условие. Дан прямой параллелепипед. В его основании лежит параллелограмм со сторонами 6 и 8 см, острый угол между которыми равен 30º. Боковое ребро имеет длину 5 см. Требуется вычислить полную площадь параллелепипеда.
Решение. Это тот случай, когда нужно узнать площади всех граней по отдельности. Или, точнее, трех пар: основание и две боковые.
Осталось объединить все в одну формулу и сосчитать:
S = 2 * (а * в * sin 30º + а * с + в * с )