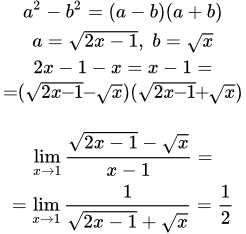Как находить пределы с корнями
Как решать пределы для чайников?
Для тех, кто хочет научиться находить пределы в данной статье мы расскажем об этом. Не будем углубляться в теорию, обычно её дают на лекциях преподаватели. Так что «скучная теория» должна быть у Вас законспектирована в тетрадках. Если этого нет, то почитать можно учебники взятые в библиотеке учебного заведения или на других интернет-ресурсах.
Итак, понятие предела достаточно важно в изучении курса высшей математики, особенно когда вы столкнетесь с интегральным исчислением и поймёте связь между пределом и интегралом. В текущем материале будут рассмотрены простые примеры, а также способы их решения.
Примеры решений
Нам часто присылают эти пределы с просьбой помочь решить. Мы решили их выделить отдельным примером и пояснить, что данные пределы необходимо просто запомнить, как правило.
Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!
Внимание «чайникам» 🙂 Чтобы вычислить предел любого типа и вида нужно подставить значение x, указанное под пределом, в функцию, стоящую под знаком предела. Давайте попробуем это сделать:
Продолжаем решать учитывая вышеприведенное преобразование:
Используя определение из примера 2 и подставляя в место х бесконечность получаем:
Чтобы устранить такую неопределенность нужно вынести за скобки икс в числителе и в знаменателе, далее их сократить. В полученное выражение подставить икс равное бесконечности. Пробуем.
Алгоритм вычисления лимитов
В этой статье Вы ознакомились с основами решения пределов, часто используемых в курсе Математического анализа. Конечно же это не все типы задач, предлагающихся экзаменаторами, а только простейшие пределы. В следующих статьях поговорим о других типах заданий, но сперва необходимо усвоить этот урок, чтобы двигаться далее. Обсудим, что делать, если есть корни, степени, изучим бесконечно малые эквивалентные функции, замечательные пределы, правило Лопиталя.
Если у Вас не получается самостоятельно решить пределы, то не паникуйте. Мы всегда рады помочь!
Решение пределов с корнями
Методы решений
Для вычисления пределов с корнями, применяются приемы и методы, аналогичные методам вычисления пределов с многочленами (см. «Раскрытие неопределенностей с дробями», «Решение пределов с дробями из многочленов»). При этом возможны следующие дополнительные приемы, специфичные для функций с корнями.
1) Убрать корни с помощью подстановки, применяя теорему о пределе сложной функции. Примеры ⇓
2) Разделить числитель и знаменатель на x s (в случае неопределенности вида ∞/∞ при x → ∞ ), где s – некоторое подобранное число. Пример ⇓
3) Выразить бесконечно малые функции, содержащие корни, через бесконечно малые линейные функции, используя приведенные ниже формулы (то же самое в случае разности бесконечно больших функций). Примеры ⇓
4) Иногда удобно бесконечно малую функцию преобразовать в сумму или разность бесконечно малых функций, пределы от которых легко находятся. Пример ⇓
Примеры решений
Решение подстановкой
Пример 1
Применим теорему о пределе сложной функции. Но поскольку функция строго монотонна, то мы применим ее разновидность – теорему о пределе функции от монотонной функции.
Теперь вычисляем второй предел:
.
Он не содержит корней. То есть мы свели задачу к пределу от разности дробей многочленов. Применяем методы, изложенные на странице «Решение пределов с дробями из многочленов».
По теореме о пределе функции от монотонной функции,
.
Пример 2
Все примеры ⇑ Найти предел последовательности:
.
Преобразуем элемент заданной последовательности, воспользовавшись свойствами корней:
.
Находим предел отношения многочленов, выделяя и сокращая в числителе и знаменателе множитель :
.
Неопределенность ∞ / ∞
Пример 3
Все примеры ⇑ Найти предел отношения корней:
.
Линеаризация бесконечно малых (больших) функций
Пример 4
Все примеры ⇑ Найти предел дроби с корнями:
.
Пример 5
Можно было записать и так:
.
После чего вычислить пределы:
.
Пример 6
Все примеры ⇑ Найти предел функции с корнями при x стремящемся к бесконечности:
.
Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин. Сборник задач по высшей математики. Том 1. Москва, 1957.
Л.Д. Кудрявцев, А.Д. Кутасов, В.И. Чехлов, М.И. Шабунин. Сборник задач по математическому анализу. Том 1. Москва, 2003.
Б.П. Демидович. Сборник задач и упражнений по математическому анализу. Москва, 1997.
Пределы с корнями
Содержание:
Основные свойства корней. Определение корня
Вообще корнем 
-й степени из числа а называется такое число, 
-я степень которого равна а.
Число п, означающее, в какой степени находится корень, называется показателем корня.
Корень обозначается знаком 
(знак радикала, т. е. знак корня). Под горизонтальной чертой его пишут то число, из которого корень отыскивается (подкоренное число), а над отверстием угла ставят показатель корня. Так:
корень кубический из 27 обозначается 
;
корень пятой степени из 32 обозначается 
.
Показатель квадратного корня принято не писать вовсе; например, вместо 
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Арифметический корень
Укажем следующие два свойства арифметического корня.
а) Пусть требуется найти арифметический 
. Такой корень будет 7, так как 
. Зададимся вопросом, нельзя ли подыскать какое-нибудь другое положительное число х, которое тоже было бы равно Предположим, что такое число существует. Тогда оно должно быть либо меньше 7, либо больше 7. Если допустим, что х 7, то тогда и 
. Значит, никакое положительное число, ни меньшее 7, ни большее 7, не может равняться 
. Таким образом, арифметический корень данной степени из данного числа может быть только один.
К другому заключению мы бы пришли, если бы говорили не только о положительном значении корня ; так, 
ж равен и числу 7, и числу —7 [так как и 
б) Возьмём каких-нибудь два неравных положительных числа, например, 49 и 64. Из того, что 49
Меньшему положительному числу соответствует и меньший арифметический корень (той же степени).
Возможно вам будут полезны данные страницы:
Алгебраический корень
Корень называется алгебраическим, если не требуется, чтобы он извлекался из положительного числа и чтобы сам он был положительный. Таким образом, если под выражением 
разумеется алгебраический корень п-й степени, то это значит, что число а может быть и положительное, и отрицательное и самый корень может быть и положительным, и отрицательным.
Укажем следующие четыре свойства алгебраического корня.
а) Корень нечётной степени из положительного числа есть положительное число.
Так, 
должен быть числом положительным (он равен 2), так как отрицательное число, возведённое в степень с нечётным показателем, даёт отрицательное число.
б) Корень нечётной степени из отрицательного числа есть отрицательное число.
в) Корень чётной степени из положительного числа имеет два значения, с противоположными знаками и с одинаковой абсолютной величиной.
Так, 
, потому что 
; точно так же 
, потому что степени 
равны одному и тому же числу +81.
Двойное значение корня обозначается обыкновенно постановкой двух знаков перед абсолютной величиной корня; так, пишут:
Чтобы в дальнейшем не оговаривать каждый раз, берём ли мы алгебраический или арифметический корень, условимся в следующем: 1) В случае чётной степени под выражением 
, 
и т. д. будем всегда подразумевать только арифметический корень. Так, 
2) Если мы берём алгебраический корень, то будем ставить перед корнем двойной знак. Так, 
г) Корень чётной степени из отрицательного числа не может равняться никакому, ни положительному, ни отрицательному, числу, так как и то и другое после возведения в степень с чётным показателем даёт положительное число, а не отрицательное. Например, 
не равен ни +3, ни —3 и никакому иному числу.
Корень чётной степени из отрицательного числа принято называть мнимым числом, остальные же числа называются вещественными, или действительными числами.
Извлечение корня из произведения, из степени и из дроби
а) Пусть надо извлечь арифметический квадратный корень из произведения abc. Если бы требовалось произведение возвести в квадрат, то, как мы видели, можно возвести в квадрат каждый сомножитель отдельно. Так как извлечение корня есть действие, обратное возведению в степень, то надо ожидать, что и для извлечения корня из произведения можно извлечь его из каждого сомножителя отдельно, т. е. что 
Чтобы убедиться в верности этого равенства, возведём правую часть его в квадрат (по теореме о степени произведения):
Но согласно определению корня:
Следовательно, 
Если же квадрат произведения 
то это значит, что произведение это равно квадратному корню из абс. Подобно этому:
Значит, чтобы извлечь арифметический корень из произведения, можно извлечь его из каждого сомножителя отдельно.
б) Легко убедиться проверкой, что следующие равенства верны.
Значит, чтобы извлечь корень из степени, показатель которой делится на показатель корня, можно разделить показатель степени на показатель корня.
в) Верны будут также и следующие равенства:
Значит, чтобы извлечь корень из дроби, можно извлечь его из числителя и знаменателя отдельно.
Напомним, что в этих правилах предполагается, что речь идёт о корнях арифметических.
Примеры с решением
Замечание. Если искомый корень чётной степени и предполагается алгебраическим, то перед найденным результатом надо поставить двойной знак ±. Так: 
Присылайте задания в любое время дня и ночи в ➔ 
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Решение пределов с корнями разных степеней
Нам понадобится несколько формул, которые я запишу ниже:
Все преобразования, применённые выше, уже были рассмотрены ранее, поэтому полагаю, особых неясностей здесь нет. Впрочем, если решение вашего аналогичного примера вызывает вопросы, прошу отписать об этом на форум.
Перед тем, как приступить к решению определите тип своей задачи
Для того, чтобы раскрывать такие неопределенности необходимо домножить числитель и знаменатель дроби на сопряженное к выражению содержащему корень.
Раскрываем скобки в знаменателе и упрощаем его:
Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!
Теперь выполняем сокращение:
Этот вид пределов часто попадается в дополнительных заданиях на экзамене. Ведь часто студенты не правильно вычисляют пределы такого типа. Как решать пределы с корнями данного вида? Всё просто. Необходимо умножить и разделить функцию, стоящую в пределе, на выражение сопряженное к ней.
После домножения и разделения на сопряженное имеем предел:
После раскрытия скобок и упрощения получаем:
Методы решений
Для вычисления пределов с корнями, применяются приемы и методы, аналогичные методам вычисления пределов с многочленами (см. «Решение пределов с дробями из многочленов»). При этом возможны следующие дополнительные приемы, специфичные для функций с корнями:
1) убрать корни с помощью подстановки, применяя теорему о пределе сложной функции; Примеры ⇓
2) разделить числитель и знаменатель на x s (в случае неопределенности вида ∞/∞ при x → ∞ ), где s – некоторое подобранное число; Пример ⇓
3) выразить бесконечно малые функции, содержащие корни, через бесконечно малые линейные функции, используя приведенные ниже формулы (то же самое в случае разности бесконечно больших функций); Примеры ⇓
4) иногда удобно бесконечно малую функцию преобразовать в сумму или разность бесконечно малых функций, пределы от которых легко находятся. Пример ⇓
Примеры решений
Решение подстановкой
Пример 1
Теперь вычисляем второй предел:
.
Он не содержит корней. То есть мы свели задачу к пределу от разности дробей многочленов. Применяем методы, изложенные на странице «Решение пределов с дробями из многочленов».
Разложим знаменатель на множители и приводим дроби к общему знаменателю:
;
Пример 2
Все примеры ⇑ Найти предел последовательности:
.
Преобразуем элемент заданной последовательности, воспользовавшись свойствами корней:
.
Находим предел отношения многочленов, выделяя и сокращая в числителе и знаменателе множитель :
Неопределенность ∞ / ∞
Пример 3
Все примеры ⇑ Найти предел отношения корней:
.
Линеаризация бесконечно малых (больших) функций
Пример 4
Все примеры ⇑ Найти предел дроби с корнями:
.
Делим числитель и знаменатель на и находим предел:
Пример 5
Применим формулу:
.
Подставим :
Наконец, применим формулу:
.
Подставим :
Можно было записать и так:
.
После чего вычислить пределы:
.
Пример 6
Все примеры ⇑ Найти предел функции с корнями при x стремящемся к бесконечности:
.
Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин. Сборник задач по высшей математики. Том 1. Москва, 1957.
Л.Д. Кудрявцев, А.Д. Кутасов, В.И. Чехлов, М.И. Шабунин. Сборник задач по математическому анализу. Том 1. Москва, 2003.
Б.П. Демидович. Сборник задач и упражнений по математическому анализу. Москва, 1997.