Как находить проценты 5 класс

Проценты. Нахождение процентов от числа

Урок 38. Математика 5 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Проценты. Нахождение процентов от числа»

– Саша, привет, чем занимаешься?

– Да. Только я не совсем понимаю. Смотри, там написано, что войско Атамана было на 15 % больше, чем войско Горыни, которое состояло из 200 воинов. И вот я не могу понять, что такое проценты и как подсчитать, сколько же воинов в войске Атамана?

– Да, интересно. Пойдём к Электроше, он нам точно сможет помочь.

– Электроша, привет. Мы к тебе с новой задачей.

– Здравствуйте, мальчики. Ну что там у вас?

– Да вот я в книге прочитал, что войско одного командира было на 15 % больше, чем войско второго командира. Но что такое проценты, мы не знаем.

– Сейчас я вам всё расскажу. Но сначала давайте выполним несколько устных заданий.

– Вернёмся к вашему вопросу.

Для сотой части величины или числа было придумано специальное название – 1 %. Происходит это слово от двух латинских слов, которые переводятся как «на сто». Обозначают процент специальным символом %.

Для того, чтобы найти процент от числа, надо число разделить на 100.

Например, 1 % от 500 килограммов равен 5 килограммам.

– Ой, Электроша. Получается, что, если для того, чтобы найти 1 %, надо разделить на 100, то для того, чтобы найти 3%, надо разделить на 300?

– Нет, ребята. Не так. Для того, чтобы найти 3% от числа, надо число разделить на 100 и умножить на 3. Так, 3 % от 500 килограммов будут равны 15 килограммам.

– А, ну тогда понятно.

– Если вам понятно, то давайте выполним одно небольшое упражнение.

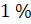
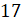
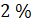
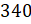
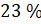
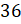
Найдите: а) от ; б) от ; в) от .Это задание для тебя, Саша.

Найдём, чему равен 1 %. Получим, что 1 % от 17 равен 0,17.

Чтобы найти, чему равны 2 % от 340, найдём, чему равен 1 %, и умножим на 2. Получим 6,8.

23 % от 36 равны 8,28.

Понятно, что само число – это 100 %.

То есть если, например, работа выполнена на 100 % или заряд батареи равен 100 %, то это значит, что работа выполнена полностью и батарея тоже полностью заряжена.

Скажите, мальчики. А где ещё мы часто слышим о процентах?

– В магазинах. Там очень часто проходят акции и скидки на 5 %, 10 %, 15 % и так далее.

– Да, вы правы. Ещё проценты активно используют в банковском деле и не только.

Чаще всего проценты используют тогда, когда нужно показать, как меняется та или иная величина.

Если, например, факультатив по математике раньше посещали 6 человек, а теперь уже посещают 12, то можно сказать, что количество учеников, которые посещают факультатив по математике, увеличилось на 100 %.

Или, например, если по акции цена товара уменьшается вдвое, то говорят, что произошло снижение цены на 50 %.

Любое количество процентов очень просто записать десятичной дробью. Вы помните, что 1 % – это одна сотая числа. Значит, 1 % можно записать дробью 0,01.

– Подожди, Электроша, получается, что 15 % можно записать как 0,15?

– Да, Паша, ты абсолютно прав.

Для того, чтобы проценты записать десятичной дробью или натуральным числом, надо число, которое стоит перед знаком %, разделить на 100.

– А разве проценты можно перевести в натуральное число?

Конечно, можно. Если у нас 100 % или 200 %, то они переведутся, соответственно, в 1 и 2.

Ещё удобно пользоваться процентами, когда мы хотим получить более точное представление о числе. Вот, например, в четверти среди текущих оценок у вас было 5 «пятёрок». Много это или мало? Не зная, сколько всего оценок по математике в четверти, ответить на этот вопрос нельзя.

Если у вас в четверти 30 оценок по математике и только 5 из них «пятёрки» – это много или мало?

– А если я скажу, что 90 % ваших оценок за четверть составляют «пятёрки», то это много или мало?

Но, Электроша, давай вернёмся к нашей задаче и попробуем узнать, сколько же всего воинов в войске Атамана.

– Хорошо. Но сначала давайте решим несколько заданий попроще, чтобы мы могли решить вашу задачу все вместе.

Груши составляют 15 % от всех фруктов на складе. Сколько килограммов груш находится на складе, если всего там располагается 60 килограммов фруктов?

Сначала найдём, сколько килограммов фруктов составляет 1 %. Для этого разделим 60 килограммов на 100. Получим, что 1 % равен 0,6 килограмма. Нам необходимо найти 15 %. Умножим 0,6 килограмма на 15 и получим, что на складе находится 9 килограммов яблок.

Такие задачи называют «задачами на нахождение процентов от числа».

Теперь мы можем вернуться к вашей задаче. Паша, попробуй сам её решить.

– Найдём, сколько воинов составляет 1 % от войска Горыни.

Для этого разделим 200 на 100 и получим, что 1 % от войска Горыни – это 2 воина.

Войско Атамана больше на 15 %, то есть на 30 человек.

Теперь к 200 прибавим 30 и получим, что в войске Атамана 230 воинов.

– Молодец, Паша. Теперь давайте рассмотрим вот такую задачу.

Вкладчик положил на счёт в банке 30 000 рублей под 8 % годовых. Давайте попробуем подсчитать, какая сумма будет на счету вкладчика через год, если он ничего не будет снимать и докладывать на счёт.

У этой задачи есть два способа решения.

Узнаем, сколько рублей составляет 1 %. Для этого 30 000 разделим на 100 и получим, что 1 % составляет 300 рублей.

Тогда 8 % составляют 2400 рублей. Тогда к концу месяца на счету вкладчика будет уже 32 400 рублей.

Эту же задачу можно решить и другим способом.

Поскольку доход со счёта составляет 8 % в год, то через год на счету будет уже лежать 108 % от первоначальной суммы.

1 % от первоначальной суммы равен 300 рублям. Тогда 108 % равны 32 400 рублям.

– Ну что, ребята, теперь вам понятно, как решать такие задачи?

Тогда вот для вас ещё одна задача.

Раствор содержит 6 % соли. Определите, сколько соли содержится в 350 килограммах раствора.

– Эта задача для тебя, Саша.

Определим, сколько килограммов составляют 1 %. Получим 3,5 килограмма. Умножим это число на 6 и получим 21 килограмм.

Теперь решите ещё одну задачу.

Участники двухдневных гонок должны были преодолеть 670 километров. В первый день они преодолели 38 % всего пути. Сколько километров гонщики преодолели во второй гоночный день?

Попробуй, Паша, решить эту задачу.

– Длина всей трассы – это 100 %. Если в первый день проехали 38 % трассы, то во второй останется преодолеть 62 %. Определим, сколько километров составляют 1 %. Получим 6,7 километра. Тогда во второй день гонщики преодолели 415,4 километра.

Решите ещё одну задачу.

Доходы фирмы за 3 летних месяца составили 280 000 рублей. В июне доходы составили 35 % от этой суммы, в июле – 110 % июньских доходов. Сколько рублей составила прибыль фирмы за август?

Сначала посчитаем, сколько рублей составляет 1 % прибыли фирмы. Получим 2800 рублей. Тогда за июнь прибыль фирмы составила 98 000.

Подожди, Электроша, но июльская прибыль составляет 110 % июньской. Как такое посчитать?

– Не волнуйся. Всё довольно просто. Для того, чтобы посчитать июльскую прибыль, мы должны найти 110 % от 98 000. Разделим это число на 100, умножим на 110 и получим, что за июль месяц прибыль составила 107 800 рублей.

– Подсчитать прибыль за август несложно. От общей суммы прибыли отнимем суммы прибыли за июнь и июль. Получится, что в августе прибыль фирмы составила 74 200 рублей.

– Интересно, а можно ли найти число по процентам?

Для того, чтобы разобраться, давайте попробуем решить одну задачу.

В молоке содержится 21 % сливок. Сколько молока надо взять, чтобы получить 10,08 килограмма сливок?

Поскольку это количество сливок составляет 21 %, значит, 1 % будет равен 0,48 килограмма.

Вес молока – это 100 %, значит, необходимо взять 48 литров молока.

Задачи именно такого вида и называют «задачами на нахождение числа по его процентам».

Вам понятно, мальчики?

– Тогда вот вам ещё одна задача для решения.

Определите, сколько времени мама потратила на приготовление ужина, если на приготовление мясных блюд понадобилось 40 % всего времени, десерт занял 20 %, а приготовление салатов заняло 48 минут.

– Саша, эта задача для тебя.

– Подсчитаем сначала, сколько процентов времени у мамы заняла готовка мясных блюд и десерта. Получим 60 % всего времени. Тогда на салаты остаётся 40 %. Разделим 48 минут на 40 и получим, что 1 % – это 1,2 минуты. Умножим это число на 100. Значит, мама на приготовление ужина потратила 120 минут, или 2 часа.

Источник

Задачи на проценты

Рассмотрим три основных типа задач на проценты.

Нахождение процента от числа

Чтобы найти процент от числа, нужно число умножить на процент.

Задача № 1569 из учебника «Виленкин 5 класс»

Предприятие изготовило за квартал 500 насосов, из которых 60% имели высшую категорию качества. Сколько насосов высшей категории качества изготовило предприятие?

Найдем 60% от 500 (общее количество насосов).

500 · 0,6 = 300 насосов высшей категории качества.

Ответ: 300 насосов высшей категории качества.

Нахождение числа по его проценту

Чтобы найти число по его проценту, нужно его известную часть разделить на то, сколько процентов она составляет от числа.

Так как задачи «процент по числу» и «число по его проценту» очень похожи и часто не сразу понятно какой тип задачи перед нами, старайтесь внимательно читать текст. Если вам встречаются слова «который», «что составляет» и «который составляет», скорее всего перед вами задача «число по его проценту».

Задача № 1536 из учебника «Виленкин 5 класс»

Ученик прочитал 138 страниц, что составляет 23% числа всех страниц в книге. Сколько страниц в книге?

Итак, нам неизвестно сколько всего страниц в книге. Но мы знаем, что часть, которую прочитал ученик ( 138 страниц) составляет 23% от общего количества страниц в книге.

Проверка: 600 > 138 (это означает, что 138 является частью 600 ).

Ответ: 600 (стр.) — общее количество страниц в книге.

Сколько процентов одно число составляет от другого

Задача № 1609 из учебника «Виленкин 5 класс»

Из 200 арбузов 16 оказались незрелыми. Сколько процентов всех арбузов составили незрелый арбузы?

Ответ: 8% — составляют незрелые арбузы от всех арбузов.

Источник

Нахождение процентов

Чтобы найти процент от чего-либо, нужно это что-либо разделить на 100 частей и полученное число умножить на нужный процент.

Например, найти 2% от 10 см.

2% = 2/100

Если перевести это задание на более понятый язык, то оно будет выглядеть следующим образом:

Найти 2/100 от 10 см

Чтобы найти дробь от числа, нужно это число разделить на знаменатель дроби, и полученный результат умножить на числитель дроби.

Итак, делим число 10 на знаменатель дроби 2/100 (то есть на 100):

10 : 100 = 0,1

Теперь 0,1 умножаем на числитель дроби 2/100 (то есть на 2):

0,1 * 2 = 0,2

Получили ответ 0,2. Значит 2% от 10 см составляет 0,2 см. А если перевести 0,2 см в миллиметры, то получим 2 миллиметра:

0,2 см = 2 мм

Значит, 2% от 10 см составляют 2 мм.

Чтобы найти процент от чего-либо, нужно выразить процент десятичной дробью, и умножить это что-либо на полученную десятичную дробь.

Например, найти 18% числа 500.

18% = 18 : 100 = 0,18

То есть надо найти 0,18 от 500.

Чтобы найти десятичную дробь от числа, нужно это число умножить на данную десятичную дробь.

Итак, умножаем 500 на 0,18:

Значит, 18% от 500 равно 90.

Источник

Проценты

Процент — это одна сотая часть числа. Отсюда следует, что два процента — это две сотых, двадцать процентов — двадцать сотых и так далее.

Величина, от которой вычисляются проценты (например, цена, длина, количество конфет и т. д.), составляет 100 своих сотых долей, то есть 100%.

Чтобы найти один процент от числа, надо разделить это число на 100.

Пример 1. Найти один процент от числа 300.

Ответ: Один процент от 300 равен 3.

Пример 2. Найти один процент от числа 27,5.

Ответ: Один процент от 27,5 равен 0,275.

Нахождение процентов от числа

Чтобы найти некоторое число процентов от данного числа, нужно данное число разделить на 100 и умножить на число процентов.

Задача 1. В том году в магазине к новому году купили 200 ёлок. В этом году количество купленных ёлок увеличилось на 120%. Сколько ёлок купили в этом году?

Решение: Сначала надо найти 120% от 200, для этого 200 надо разделить на 100, так мы найдём 1%, а затем полученный результат умножить на 120:

(200 : 100) · 120 = 240.

Число 240 — это 120% от 200. Значит, в этом году количество проданных ёлок увеличилось на 240 штук. То есть, количество ёлок, проданных в этом году равно:

200 + 240 = 440 (ёлок).

Ответ: В этом году купили 440 ёлок.

Задача 2. В коробке 28 конфет, 25% конфет с клубничной начинкой. Сколько конфет с клубничной начинкой в коробке?

Ответ: В коробке 7 конфет с клубничной начинкой.

Нахождение числа по его процентам

Чтобы найти число по данной величине его процентов, нужно эту величину разделить на число процентов и умножить на 100.

Задача. Цена метра сукна снизилась на 24 руб., что составило 15% цены. Сколько стоил метр сукна до снижения?

Ответ: Метр сукна стоил 160 рублей.

Процентное отношение двух чисел

Чтобы узнать, сколько процентов первое число составляет от второго, надо первое число разделить на второе и результат умножить на 100.

Задача. Завод по годовому плану должен выпустить продукции на сумму 1 250 000 руб. За 1-ый квартал он выпустил её на сумму 450 000 руб. На сколько процентов выполнен заводом годовой план за 1-ый квартал?

Ответ: За 1-ый квартал план выполнен на 36%.

Перевод процентов в десятичную дробь

Чтобы перевести проценты в десятичную дробь, надо количество процентов разделить на 100.

Пример 1. Представить 25% в виде десятичной дроби.

Пример 2. Выразить 100% десятичной дробью.

Пример 3. Выразить 230% десятичной дробью.

Источник

Задачи на нахождение процента

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Понятие процентов

Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить число на 100.

А если нужно перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %.

А вот, как перевести проценты в десятичную дробь — обратным действием:

Примеры с процентами

Пример 1

Найдите 60% от числа 250.

Решение:

Число 250 будет нашим целым, то есть это 100%. Нам нужно найти 60%. Отношение 60 к 100 будет равно отношению неизвестного числа к 250:

Произведение крайних будет равно произведению внутренних, то есть 100 умножить на Х равно 250 умножить на 60:

Решаем простое уравнение и получаем 150.

Ответ: 150

Пример 2

Найдите число, если его 40% равняется 100.

Решение:

Решаем по алгоритму из первого примера, только здесь неизвестен один из крайних элементов.

Ответ: 250

Примеры задач на проценты с решением

Для полного понимания задач на проценты, необходимо решить реальные примеры из жизни. Этим и займемся🤓

Задача 1

Интернет-магазин закупился 1000 айфонами. Но вот беда: 3% процентов из них оказались бракованными. Сколько айфонов из 1000 бракованные?

Решение:

Всего у магазина 1000 айфонов — это 100%. Отношение 3% к 100 будет равно отношению бракованных айфонов к их общему количеству:

Ответ: 30 айфонов — бракованные.

Задача 2

Школа купила 250 парт: 225 из них — полностью годны для использования. Какой процент парт исправны, а сколько процентов оказались браком?

Решение:

250 парт — это 100 процентов. По простой пропорции отношения исправных парт к общему числу и их процентов к 100 находим долю.

225 х 100 = 250 х Х

90 процентов парт — готовы разбежаться по кабинетам, с ними все в порядке. Значит с остальными партами что-то не так: то ли ножки кривые, то ли краска слезла. Выходит: 100 – 90 = 10. 10 процентов парт бракованы.

Ответ: 90% годны и 10% бракованы.

Задача 3

Цена за килограмм арбуза увеличилась на 8 рублей — это на 10% больше прежней цены. Сколько раньше стоил килограмм арбуза?

Решение:

Если 8 рублей — это 10 процентов, то по пропорции находим 100%.

Ответ: до подорожания арбуз стоил 80 рублей за килограмм.

Задача 4

Число собачек-мальчиков в питомнике относится к числу всех собак, как 1/15. Общее число собак в питомнике — 120. Сколько всего собак-мальчиков и каков их процент?

Решение:

Сначала нужно найти число собак-мальчкиков. Нам дано отношение 1/15. По пропорции находим:

Число собак-мальчиков — 8. Всего их 120, то есть по еще одной пропорции находим их долю.

Ответ: 6.67 процентов собак — мальчики, а всего их 8.

Задача 5

25% фотографий в инстаграме одноклассника — это 150 штук. Сколько всего у него фоток в аккаунте?

Решение:

Если 25% — это 150, то нужно найти значение 100 процентов.

Ответ: у одноклассника 600 фотографий.

Задача 6

Артем купил 15 яблок — 3 из них оказались гнилыми. Он выбросил их и купил еще 8. Теперь гнилых яблок было 2, а яблок всего 20. Насколько процентов снизилась доля гнилых яблок?

Решение:

Сначала гнилых яблок было 3 из 15 — это 20% от общего количества.

Потом Артем купил еще 8 — теперь их стало 20. Но 2 яблока оказались гнилыми. То есть процент гнилых яблок теперь стал 10%.

Ответ: процент гнилых яблок снизился на 10%

Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Источник