Как находить расстояние по меридианам
Как измерить расстояние на карте с помощью градусной сетки?
С помощью карты можно определять расстояние между точками на земной поверхности, но точность таких вычислений невысока.
Ситуация относительно проста, если точки лежат на одном меридиане. Все меридианы имеют одинаковую длину. Можно подсчитать, что одному градусу широты соответствует примерно 111,3 км реальной длины. Поэтому надо найти разницу в долготе между точками и умножить ее на 111,3 км. Например, если точка А находится на северной широте 50°, а Б располагается на северной широте 32°, и при этом у них совпадает долгота, то расстояние между ними составит.
111,3х(50° – 32°) = 111,3х16 = 1780,8 км
Ситуация меняется, когда одна точка имеет северную, а другая – южную широту. В этом случае широты уже надо складывать. Так, если бы точка Б из предыдущего примера располагалась бы на южной широте 32°, то расстояние от А до Б составило бы:
111,3х(50° + 32°) = 111,3х82 = 9126,6 км
Ситуация усложняется, когда точки находятся на разных меридианах, но на одной параллели. Если у обеих точек долгота западная (или, наоборот, восточная), то сначала надо найти разницу их долгот. Если же одна точка имеет восточную, а другая западную долготу, то их надо суммировать. Далее результат надо умножить на длину 1° параллели. Эта длина у параллелей различна и зависит от их широты. Можно воспользоваться таблицей ниже:
| Широта параллели | Длина ее дуги величиной в 1° |
|---|---|
| 0° | 111,3 |
| 5° | 110,9 |
| 10° | 109,6 |
| 15° | 107,6 |
| 20° | 104,6 |
| 25° | 102,1 |
| 30° | 96,5 |
| 35° | 91,3 |
| 40° | 85,4 |
| 45° | 78,8 |
| 50° | 71,7 |
| 55° | 64,0 |
| 60° | 55,8 |
| 65° | 47,2 |
| 70° | 38,2 |
| 75° | 28,9 |
| 80° | 19,4 |
| 85° | 9,7 |
| 90° | 0 |
Например, нужно найти расстояние между точками, имеющими координаты:
А – 60° с. ш, 39° з. д.
Б – 60° с. ш, 25° з. д.
Широты у них одинаковы, поэтому смотрим на долготу. Она у обеих точек западная, поэтому надо найти их разницу:
39° – 25° = 14°
Полученный результат надо умножить на длину 1° параллели, широта которой составляет 60°. По табличке определяем, что на широте 60° дуга в 1° имеет длину 55,8 км. Перемножаем два числа:
14°х 55,8 км = 781,2 км
Список использованных источников
Презентация по географии «Измерение расстояний по карте с помощь градусной сетки»
Описание презентации по отдельным слайдам:
Измерение расстояний с помощью градусной сетки
Меридиан Линия на карте соединяющая северный полюс и южный полюс земли. Все меридианы – одинаковой длины. Длина 1° составляет – 111,3 км.
Определение расстояния по меридиану 1. Определить расстояние в градусах между точками 2. Умножить число градусов на 111, 3 км
Пример: Длина дуги 1° меридиана приблизительно равна 111,3 км (20000 км : 180°= 111,3 км). А=(ш1+ш2)×111,3=(20°+10°) ×111,3= 30°⋅ 111,3= 3339 км. Б= (ш1 – ш2) ⋅ 111,3= (40°– 10°) ⋅ 111,3= 30°⋅ 111,3= 3339 км. В= (ш2 – ш1) ⋅ 111,3= (30°– 10°) ⋅ 111,3= 20°⋅ 111,3= 2226 км.
Параллель Длины дуг величиной 1° для разных параллелей неодинаковы — они уменьшаются от экватора к полюсам. широта 0 5 10 15 20 25 30 35 40 45 Длина 1°в км 111,3 110,9 109,6 107,6 104,6 102,1 96,5 91,3 85,4 78,8 широта 50 55 60 65 70 75 80 85 90 Длина 1°в км 71,7 64,0 55,8 47,2 38,2 28,9 19,4 9,7 0
Определение расстояний по параллели Определить расстояние в градусах Прочесть на карте полушарий длину 1 градуса по нужной вам параллели Умножить длину 1 градуса на число градусов
Длины дуг величиной 1° для разных параллелей неодинаковы — они уменьшаются от экватора к полюсам. А= (д1+ д2) ⋅ 104,6 (длина 1° на широте 20°) = (10°+ 20°) ⋅ 104,6= 30° ⋅ 104,6= 3138 км. Б= (д1 – д2) ⋅ 109,6= (20°– 10°) ⋅ 109,6= 10°⋅ 109,6= 1096 км. В= (д2 – д1) ⋅ 96,5= (90°– 60°) ⋅ 96,5= 30°⋅ 96,5= 2895 км.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс профессиональной переподготовки
География: теория и методика преподавания в образовательной организации
Курс повышения квалификации
Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС
Ищем педагогов в команду «Инфоурок»
Данная презентация может быть использована на уроке географии при изучение темы «Определение расстояния по карте». В работе подробно рассказано о линиях градусной сетки. Дано определение меридиан и параллель.
По шагово объяснено как определить расстояние между точками по меридиану и параллелям. Приведены примеры.
Номер материала: ДБ-576504
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В Минпросвещения рассказали о формате обучения школьников после праздников
Время чтения: 1 минута
Петербургский Политех перевел студентов на дистанционку
Время чтения: 1 минута
Все школы РФ с 2023 года подключат к государственной информационной системе «Моя школа»
Время чтения: 1 минута
В Липецкой области начинающие педагоги получат 120 тысяч рублей
Время чтения: 0 минут
Путин призвал повышать уровень общей подготовки в колледжах
Время чтения: 1 минута
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Планирование экспедиции. Геодезия и отвага
Это продолжение истории Экваториальной Градусной экспедиции в XVIII веке отправившейся к, как следует из названия, экватору, чтобы уточнить форму Земли.
Нашу научную экспедицию к берегам Перу мы оставили в том месте, где морской министр Франции, выделивший государственный бюджет на проект, пришел в ужас от кадровой политики ученых и сам занялся подбором персонала, выделением кредитов и денег, а также дипломатической перепиской с испанским двором. Луи Годену, как идеологу, оставалось лишь позаботиться о плане работ и инструментах.
Планирование работ
Планирование работ происходило в публичном пространстве кофеен и трактиров, широко обсуждалось в уже упомянутом нами Градо и в личной переписке всей ученой братии. Над чашками и бокалами разворачивались карты (довольно устаревшие) и шли ожесточенные споры.
Луи Годен, руководитель, ослепленный легким успехом, заявляет о том, что лучше измерить длину не 1 градуса меридиана (около 111 км), а целых четырех. Определенный смысл в этом действительно есть: чем большее расстояние мы измеряем, тем больше мы в безопасности от влияния случайных погрешностей. Но четыре градуса! Почти четыре с половиной сотни километров в малоизученном высокогорье, на которое и карт-то толком нет!
Красным помечена предлагаемая к измерению дуга меридиана.
В чем заключалась задача экспедиции? Требовалось измерить длину дуги меридиана в 1 градус на экваторе и сравнить, на сколько туазов (это местная мера длины) она отличается от 1 градуса Парижского меридиана.
На злобу дня в Академию пришло едкое письмо из России, где в самом вежливом тоне Жозеф Делилль, создатель Санкт-Петербургской обсерватории, предложил коллеге не мелочиться и, чего уж, измерить дугу меридиана до самой Огненной Земли. Чтобы дважды не ходить. Впрочем, Делилль имел право быть сколько угодно резким: Годен был его учеником.
«Осип Николаевич» Делилль (отец российской астрономии), гравюра Конрада Вестрмайра, Википедия).
Маленькая историческая справка
В 1735 году, о котором мы говорим, в России царствовала Анна Иоанновна, племянница Петра I: Екатерина I уже умерла, а ее дочь Елизавета еще не захватила престол. Кстати, если вы окажетесь в Москве, сходите поглядеть на Царь-колокол. Когда Луи Годен готовил свою экспедицию, Царь-колокол отливали в Кремле в специально подготовленной яме. А в Академии Наук Петербурга за астрономию отвечал Жозеф Николя Делилль, приглашенный из Парижа еще Петром I.
Про проекции хочу немного пояснить
Помните старую шутку:
Никто не сделал больше для величия России, чем проекция Меркатора.
Судя по общественному резонансу, слишком многие приняли изящный юмор за чистую монету. Дело в том, что нельзя просто так взять и перенести (земной) шар (мы же еще про XVIII век) на плоскость.
Цилиндрическая проекция Меркатора из https://gisgeography.com/cylindrical-projection/
Россия, однако, далеко от экватора и вытянута с востока на запад. Получаются сплошные искажения. Поэтому Делилль в своем XVIII веке придумал специальный подвид конической проекции.
Коническая проекция из «В.Н. Попов, С.И. Чекалин. Геодезия: Учебник для вузов.- М.: «Горная книга», 2007.»
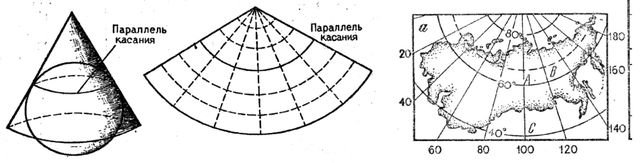
Тут земной шар оборачивается конусом, а значит «соприкосновение» бумаги с шаром идет по параллели. Профит: меньше искажений на нашу большую территорию.
Кстати, Делилль тоже пытался заниматься градусными измерениями: года через два после Луи Годена. Но ему сократили финансирование, поскольку для нашей страны эта сугубо научная (как тогда казалось) задача не была первостепенной. Увы, карьера ученого в Петербурге завершилась бесславно. Он оказался замешан в шпионском скандале (то ли правда было за что, а то ли политическая борьба за место директора обсерватории) и вернулся в Париж к 1747 году. Зато в России весь XVIII век для измерения температуры использовали градусы Делилля. Но вернемся к основному повествованию.
Как измерить длину дуги меридиана?
Градусные измерения Эратосфена: известно расстояние L в линейной мере и градусной: разность широт между точками.
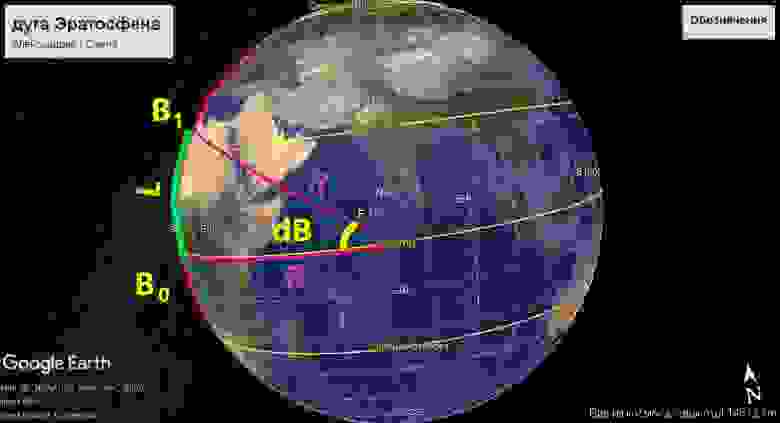
Как триангуляция появилась в геодезии?
Был такой голландский ученый, живший в XVI веке, Эратосфен Батавский (в те времена было принято брать себе хвастливые прозвища, подражая ученым древности), он же Виллеборд Снелл. Именно он использовал и популяризировал известную из математики триангуляцию для геодезических работ.
Подобно Эратосфену, Снелл тоже выполнял градусные измерения для определения радиуса Земли. Ему тоже нужно было найти длину дуги меридиана в градусах и в линейной мере (милях, к примеру). Однако караванов с погонщиками в северной Европе не было, так что расстояние пришлось определять самостоятельно.
Как устроена триангуляция?
Предположим, мы хотим найти расстояние между весьма удаленными точками (допустим удаленных на 100 километров). Просто измерить это расстояние невозможно: нет прямой видимости, нет возможности хотя бы построить прямую линию между точками (ведь одна может находиться на холме а другая на низменности, между ними могут быть реки, овраги и озера. На помощь приходит цепочка треугольников.
Это звено триангуляции АВ
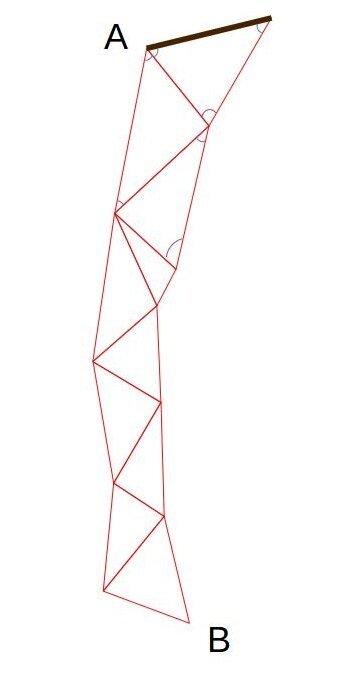
Допустим, нам нужно найти расстояние (АВ). Мы строим цепочку стыкующихся треугольников вокруг этой линии и измеряем небольшую (до 10 км) сторону треугольника A-1.
Современный (конец ХХ века) пункт триангуляции в Тульской области.
Вернемся к Экваториальной экспедиции 1735 года. Что именно предстояло сделать ученым?
Схема триангуляции из журнала Лакондамина.
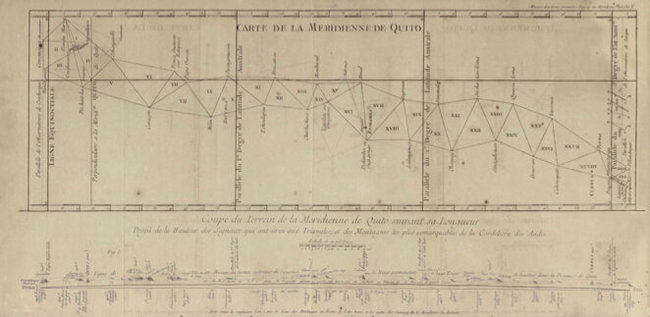
Ученые решают разбить вдоль меридиана (с севера на юг) цепочку треугольников. Треугольники требуется делать по возможности равносторонними или хотя бы равнобедренными, на местности необходимо обеспечить видимость хотя бы на две соседние вершины. Учитывая расстояния и сложности местного рельефа, треугольников по плану двадцать семь. Длина стороны в них около 30-40 км.
На современную карту тут наложены треугольники перуанской экспедиции (примерный экскиз)
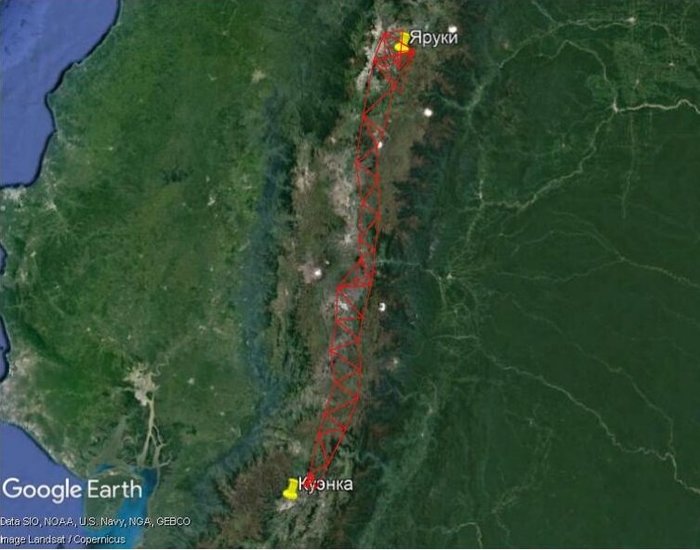
Измерена будет сторона одного из северных треугольников (базис в районе Яруки) и еще одна сторона на юге (базис в Куэнке), для контроля результатов. К сожалению, ввиду того, что это горная цепь с ущельями, скалами, реками и провалами, удобное плато для базиса было найти трудно, поэтому его длина существенно меньше (раза в четыре), чем длины сторон основных треугольников. Базис составит около 12 км. Во всех прочих треугольниках будут измерены внутренние углы. После этого ученые последовательно вычислят длины сторон всех треугольников.
Казалось бы: как теперь из наклонных сторон треугольников получить длину меридиана? Ученые будут вычислять длину проекции каждой западной стороны треугольника на меридиан. В сумме они дадут длину дуги меридиана:
Искомую длину меридиана вычисляли по сумме проекций сторон треугольника на меридиан
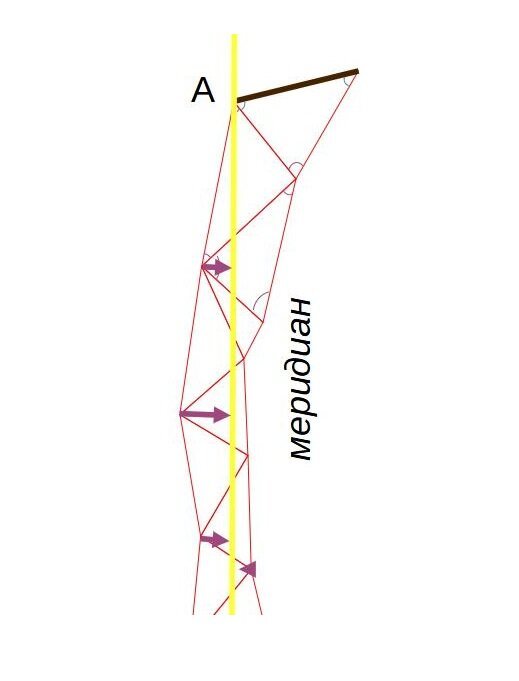
Кстати, вот любопытный факт про измеряемую сторону треугольника (базис, как он называется в триангуляции):
Деллиль в России (и еще кое-то из его коллег в Швеции) считал, что удобно будет измерять базис по замерзшему льду реки или залива, поскольку он образует ровную, поверхность с идеальной видимостью. Очень крутая и новаторская по тем временам мысль. Увы, замерзающих заливов в Перу не было.
Тот план, который Годен изначально представил в Академии, касался измерений в горной долине между западной и восточной цепью Анд. Это казалось разумным: горные вершины послужат отличным ориентиром для наблюдений, а города Кито (на севере) и Куэнка (на юге), упомянутые на карте, должны иметь хоть какие-то подъездные дороги. Однако потом Годен увлекся идеей измерять не меридиан, а параллель, его коллеги вообще хотели держаться ближе к побережью, так что планирование миссии застопорилось и окончательный ответ на вопрос “а что именно мы там будем делать?” не был дан до самого отплытия из Франции.
«Удобная для измерений» горная долина Кито, Википедия.
В защиту такого подхода руководителя миссии следует сказать, что предварительная подготовка работ велась по очень приблизительным картам, самой свежей из которых было лет двадцать. Последним французом, побывавшим в Перу был Амеде Франсуа Фрезье (торговец, инженер и шпион).
Картматериалы из «Описания путешествия» Фрезье, 1712 г.
Любопытно, что широко известен он совсем не разведдеятельностью, а клубничным десертом. Именно он привез чилийскую землянику в королевскую оранжерею. И свое французское имя fraise, ананасная земляника, ее потомок, носит по его фамилии. В общем, планирование экспедиции, хотя и было занимательным, содержало слишком много белых пятен. Все станет понятно на местности. А пока следовало позаботиться об инструментах.
Материал по географии «Определение протяжённости объектов с помощью градусной сетки»
Описание разработки
с Cевера на Юг
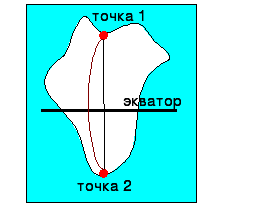
А) Если объект расположен по обе стороны от экватора
1. Определить географическую широту точек:
2. Сложить полученные данные:
(получим расстояние в градусах)
3. Умножить расстояние на 111
( так как в 1 0 по меридиану 111 км )
4. Ответ: протяжённость объекта 6660 км
Содержимое разработки
А) Если объект расположен по обе стороны от экватора
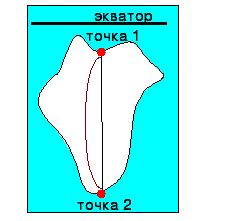
Б) Если объект расположен по одну сторону от экватора
1. Определить географическую широту точек:
2. Сложить полученные данные:
(получим расстояние в градусах)
3. Умножить расстояние на 111
( так как в 1 0 по меридиану 111 км )
4. Ответ: протяжённость объекта 6660 км
1. Определить географическую широту точек:
2. Вычесть из широты т.2 широту т.1:
(получим расстояние в градусах)
3. Умножить расстояние на 111
( так как в 1 0 по меридиану 111 км )
4. Ответ: протяжённость объекта 3774 км
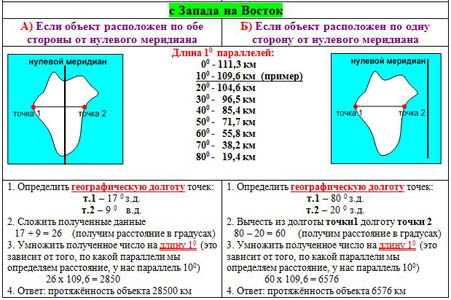
с Запада на Восток
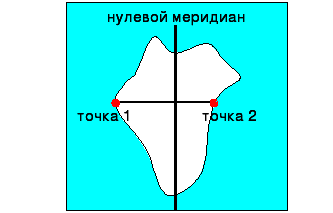
А) Если объект расположен по обе стороны от нулевого меридиана
Б) Если объект расположен по одну сторону от нулевого меридиана
Длина 1 0 параллелей:
1. Определить географическую долготу точек:
2. Сложить полученные данные
17 + 9 = 26 (получим расстояние в градусах)
3. Умножить полученное число на длину 1 0 (это зависит от того, по какой параллели мы определяем расстояние, у нас параллель 10 0 )
4. Ответ: протяжённость объекта 28500 км
1. Определить географическую долготу точек:
2. Вычесть из долготы точки1 долготу точки 2
80 – 20 = 60 (получим расстояние в градусах)
3. Умножить полученное число на длину 1 0 (это зависит от того, по какой параллели мы определяем расстояние, у нас параллель 10 0 )
Как определить географические координаты
Понятие координат включает в себя угловые и линейные числа, с помощью которых определяется положение конкретной точки в пространстве или на поверхности. С помощью этих показаний можно ориентироваться на любой местности и даже создавать собственные карты.
Конечно, для этого нужно знать, как правильно определить географические координаты, чтобы расположение объекта отображалось максимально точно. Сейчас на помощь туристам приходят современные GPS навигаторы, но иметь навыки в определении координат вручную все равно полезно, ведь это поможет сориентироваться и составить маршрут даже вдали от цивилизации.
Инструкция, как определить географические координаты
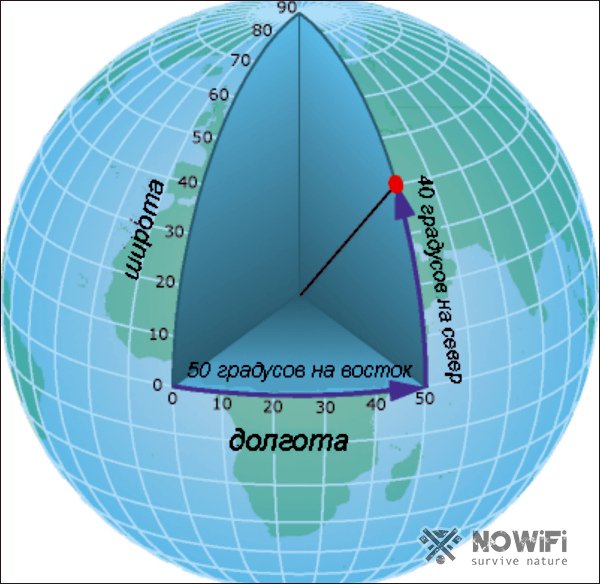
Определение географических координат начинается с установки двух величин: широты и долготы, которые отображаются в градусах (рисунок 1).
Проще всего определить широту. Если точка располагается в северном полушарии, ее координаты (ширина) тоже будут северными, а если в южном, то, соответственно, южной. Для определения широты на любую карту или глобус нанесены продольные линии – параллели, которые располагаются параллельно экватору. У экватора нулевой градус, а у полюсов этот показатель ровняется 90 градусам.
Рисунок 1. Для определения координат нужна широта и долгота
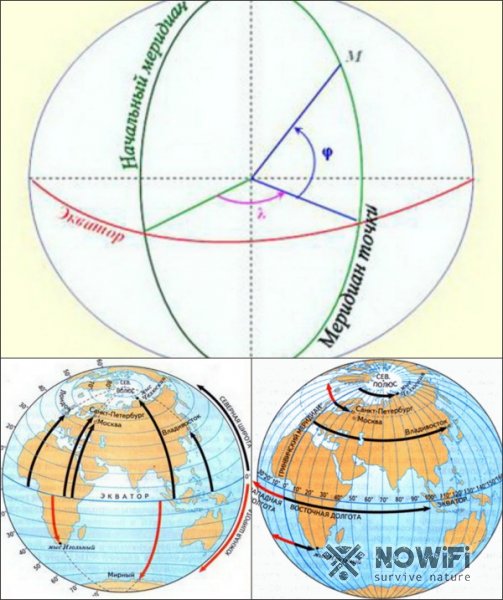
Вторым необходимым показателем является долгота. Она отображает расстояние от нулевого меридиана в Гринвиче до определенной точки на местности. Долгота бывает западной и восточной. Этот показатель определяется меридианами, которые проходят по карте или глобусу вертикально и параллельно нулевому. Сложив координаты двух точек вместе, можно получить точные данные о местоположении объекта.
Основные понятия
Из предыдущего раздела можно сделать вывод, что показатели широты и долготы являются основными координатами для определения положения объекта на местности.
Однако, если нужно знать расположение какого-то конкретного места, которое не занимает большую площадь, дополнительно понадобятся и другие данные, в частности, минуты и секунды. Это более точные координаты, с помощью которых можно определить положение объекта вплоть до нескольких километров. Как правило, эти данные используются в высокоточных картах и в военной топографии, но могут пригодиться и туристам.
Замер расстояний с помощью градусной сетки
Определять географические координаты проще всего с помощью градусной сетки. Она нанесена на любую карту или глобус и позволяет определить точное местоположение объекта на местности.
Эти данные используются для определения расстояний по карте. Зная координаты определенных объектов на карте, можно рассчитать примерное расстояние между ними, так как каждый градус равен 111,1 км. В данном случае роль играет направление расположения объектов (рисунок 2).
К примеру, если расстояние высчитывается с севера на юг, нужно сначала определить широту северного и широту южного пункта, а затем умножить получившееся число на 111,1. Этого достаточно, так как длина меридианов в любой точке планеты является примерно одинаковой.
Рисунок 2. Так выглядит градусная сетка
Расчеты расстояний с востока на запад сложнее. В случае с широтой длина параллели уменьшается к полюсам. Например, на экваторе она составляет 111 км, на 20 градусе северной или южной широты составляет уже 105 км, а на полюсах уменьшается до нуля. Именно поэтому нужно точно знать количество километров, соответствующее одному градусу на каждой широте. На 40 градусе северной широты один градус равен 85,4 км, а на 60 – уже 55,8 км. К счастью, это число указано на каждой параллели на глобусах и картах. Итак, сначала придется узнать долготу искомых объектов, а потом ориентироваться на их местоположение. Если оба объекта расположены в восточном полушарии, достаточно определить разницу между ними в градусах. Если долгота разная, разницу нужно умножить на соответствующее количество километров для каждой параллели.
Географический градус
Положение любого объекта на топографической карте определяется в градусах. Фактически, этот показатель измеряет углы от центра Земли до определенной точки на поверхности планеты, причем форма Земли в данном случае принимается за сферу.
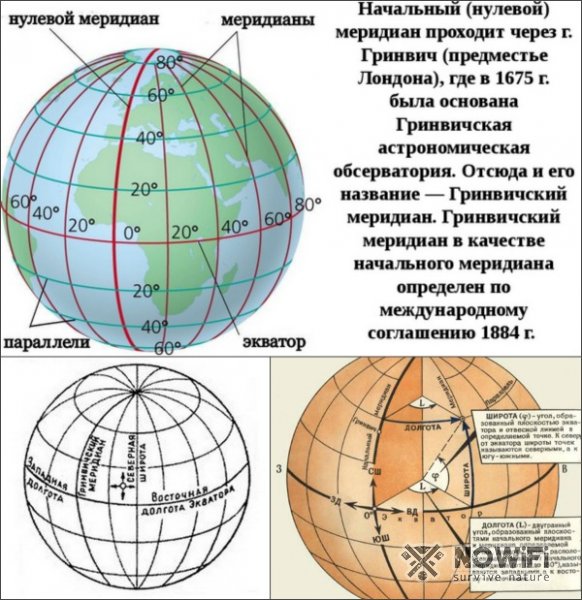
Соответственно, сфера (планета) делится на равные части (градусы). Вся окружность разделяется на 360 градусов, каждый из которых, в свою очередь, состоит из 60 минут, а в одной минуте есть 60 секунд. Зная все эти данные можно весьма точно определить местоположение объекта на карте (рисунок 3).
Рисунок 3. Градус позволяет более точно определить расположение объекта на местности
Экватор считается нулевым градусом. В северном полушарии значения широты положительные, а в южном – отрицательные. Долгота, в свою очередь, определяет углы по направлению с востока на запад, а отсчет ведется от нулевого меридиана в Гринвиче. К западу от него значения будут отрицательными, а к востоку – положительными.
Чтобы проще понять эту сложную систему, приведем пример. Американский город Лос-Анджелес лежит на широте плюс 33 градуса (так как расположен в северном полушарии) и долготе минус 118 градусов, поскольку расположен к западу от Гринвича.
Правила определения долготы и широты
Из всего написанного выше можно сделать вывод, что для определения координат по карте решающую роль играют широта и долгота, поэтому крайне важно научиться определять их.
Сначала остановимся на широте. Нулевой точкой отсчета здесь считается экватор с нулевым градусом. От него к полюсам расходятся параллели. На полюсе широта составляет 90 градусов, а все точки, расположенные на равном удалении от экватора в сторону одного из полюсов, имеют одинаковую северную или южную широту (например, 20, 40 или 60 градусов). При этом, чем дальше объект на карте от экватора и ближе к полюсу, тем больше будет его широта (рисунок 4).
Рисунок 4. Схемы определения широты и долготы
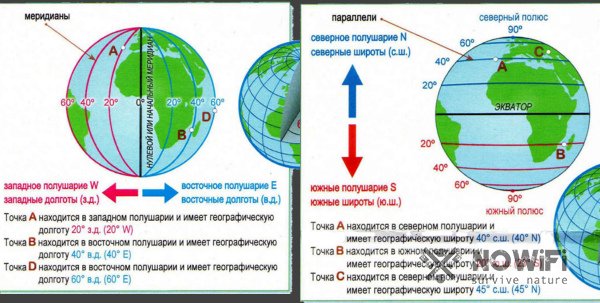
Географическая долгота на картах и глобусах отсчитывается от меридиана в Гринвиче, который считается нулевым. Здесь, как и в случае с широтой, удаление от этого меридиана приводит и к увеличению долготы. При этом максимальный показатель долготы составляет 180 градусов, поскольку полная окружность сферы (восточного и западного полушария) составляет 360 градусов.
Чтобы определить по карте географические координаты объекта, нужно сделать следующее:
В результате вы получите точную широту и долготу, а также определенное количество градусов для каждого показателя, которые уточняют расположение объекта.
Максимальное значение координат
Поскольку Земля имеет форму сферы, полная ее окружность в градусах будет составлять 360. Соответственно, долгота, которая делит планету на два полушария (восточное и западное) будет иметь максимальное значение 180 градусов для каждого из них.
Максимальное значение широты составляет 90 градусов, где 0 – это географическая координата любой точки на экваторе, а 90 – значение для каждого полюса (северного и южного).
Детальная инструкция по определению географических координат приведена в видео.