Как находить синусы косинусы тангенсы

Синус, косинус, тангенс в прямоугольном треугольнике

Гипотенузой называется та сторона треугольника, что лежит против угла в 90 градусов, две оставшиеся стороны называются катетами прямоугольного треугольника.

Подробнее про прямоугольный треугольник здесь.

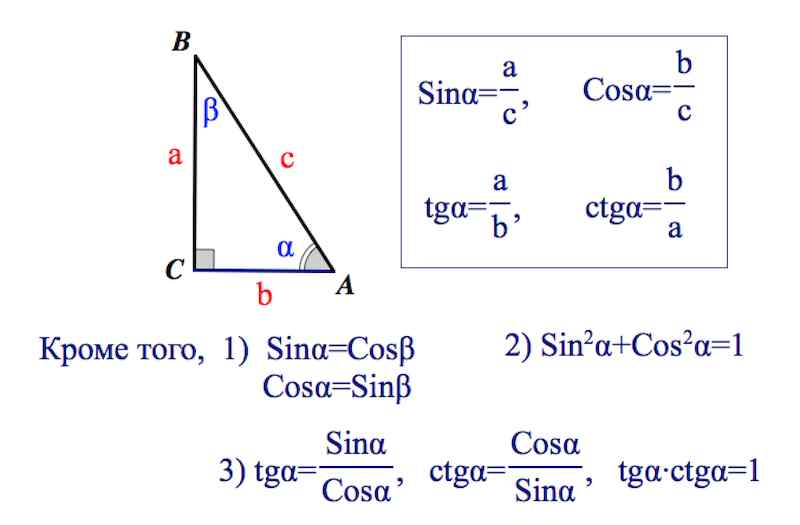
Синусом угла в прямоугольном треугольнике называется отношение противолежащего катета к гипотенузе.

Косинусом угла в прямоугольном треугольнике называется отношение прилежащего катета к гипотенузе.

Тангенсом угла в прямоугольном треугольнике называется отношение противолежащего катета к прилежащему.

Котангенсом угла в прямоугольном треугольнике называется отношение прилежащего катета к противолежащему.

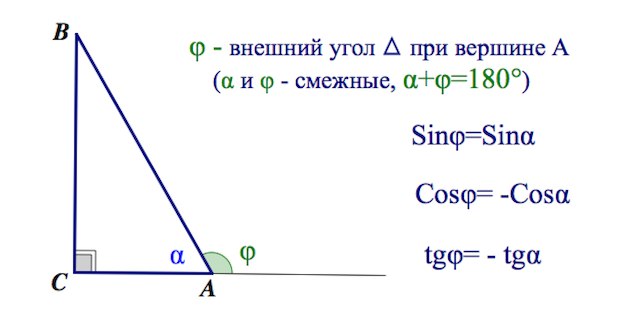
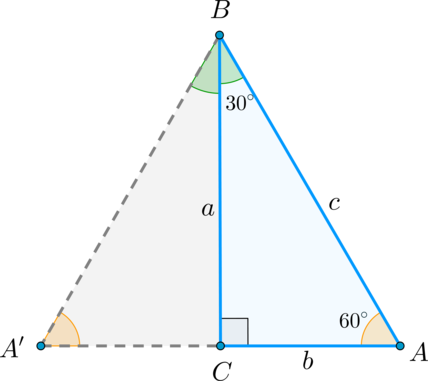
Бывает (и на ЕГЭ, ГИА), что приходится иметь дело с косинусами, синусами и тангенсами внешних углов треугольника. Формулы приведения позволяют увидеть, что есть еще и вот такая связь между смежными углами (помимо того, что их сумма равна 180):

Смотрите подборку задач на применение указанных соотношений в статье «Прямоугольный треугольник. Вычисление длин и углов» часть I, часть II.

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Источник

Синус, косинус, тангенс и котангенс (ЕГЭ 2022)

Понятия синуса, косинуса, тангенса, котангенса неразрывно связаны с понятием угла.

Не так страшен черт, как его малюют!

Чтобы хорошо разобраться в этих понятиях (нет, не в чёрте! в тригонометрии 🙂 ), начнём с самого начала.

Синус, косинус, тангенс, котангенс — коротко о главном.

Синус угла — это отношение противолежащего (дальнего) катета к гипотенузе

Косинус угла — это отношение прилежащего (близкого) катета к гипотенузе

Тангенс угла — это отношение противолежащего (дальнего) катета к прилежащему (близкому)

Котангенс угла — это отношение прилежащего (близкого) катета к противолежащему (дальнему).

Понятие угла: радиан, градус

Давай для начала разберёмся в понятии угла.

Посмотрим на рисунок.

Вектор \( AB\) «повернулся» относительно точки \( A\) на некую величину. Так вот мерой этого поворота относительно начального положения и будет выступать угол \( \alpha \).

Что же ещё необходимо знать о понятии угла? Ну, конечно же, единицы измерения угла!

Угол, как в геометрии, так и в тригонометрии, может измеряться в градусах и радианах.

Углом в \( 1<>^\circ \) (один градус) называют центральный угол в окружности, опирающийся на круговую дугу, равную \( \frac<1><360>\) части окружности.

Таким образом, вся окружность состоит из \( 360\) «кусочков» круговых дуг. То есть угол, описываемый окружностью, равен \( 360<>^\circ \).

То есть на рисунке выше изображён угол \( \beta \), равный \( 50<>^\circ \), то есть этот угол опирается на круговую дугу размером \( \frac<50><360>\) длины окружности.

Углом в \( 1\) радиан называют центральный угол в окружности, опирающийся на круговую дугу, длина которой равна радиусу окружности.

Ну что, разобрался? Если нет, то давай разбираться по рисунку.

Итак, на рисунке изображён угол \( \gamma \), равный \( 1\) радиану.

То есть этот угол опирается на круговую дугу, длина которой равна радиусу окружности (длина \( AB\) равна длине \( BB’\) или радиус \( r\) равен длине дуги \( l\)).

Таким образом, длина дуги вычисляется по формуле:

\( l=\theta \cdot r\), где \( \theta \) — центральный угол в радианах.

Ну что, можешь, зная это, ответить, сколько радиан содержит угол, описываемый окружностью?

Да, для этого надо вспомнить формулу длины окружности. Вот она:

Ну вот, теперь соотнесём эти две формулы и получим, что угол, описываемый окружностью равен \( 2\pi \).

То есть, соотнеся величину в градусах и радианах, получаем, что \( 2\pi =360<>^\circ \).

Соответственно, \( \pi =180<>^\circ \).

Как можно заметить, в отличие от «градусов», слово «радиан» опускается, так как единица измерения обычно ясна из контекста.

А сколько радиан составляют \( 60<>^\circ \)?

Уловил? Тогда вперёд закреплять:

Тогда смотри ответы:

Cинус, косинус, тангенс, котангенс угла в прямоугольном треугольнике

Итак, с понятием угла разобрались. А что же всё-таки такое синус, косинус, тангенс, котангенс угла?

Давай разбираться. Для этого нам поможет прямоугольный треугольник.

Как называются стороны прямоугольного треугольника?

Всё верно, гипотенуза и катеты.

Гипотенуза — это сторона, которая лежит напротив прямого угла (в нашем примере это сторона \( AC\))

Катеты – это две оставшиеся стороны \( AB\) и \( BC\) (те, что прилегают к прямому углу).

Причём, если рассматривать катеты относительно угла \( \angle BAC\), то катет \( AB\) – это прилежащий катет, а катет \( BC\) — противолежащий.

Итак, теперь ответим на вопрос: что такое синус, косинус, тангенс и котангенс угла?

Синус угла – это отношение противолежащего (дальнего) катета к гипотенузе.

В нашем треугольнике \( \sin \beta =\frac\).

Косинус угла – это отношение прилежащего (близкого) катета к гипотенузе.

В нашем треугольнике \( \cos \beta =\frac\).

Тангенс угла – это отношение противолежащего (дальнего) катета к прилежащему (близкому).

В нашем треугольнике \( tg\beta =\frac\).

Котангенс угла – это отношение прилежащего (близкого) катета к противолежащему (дальнему).

В нашем треугольнике \( ctg\beta =\frac\).

Эти определения необходимо запомнить!

Чтобы было проще запомнить какой катет на что делить, необходимо чётко осознать, что в тангенсе и котангенсе сидят только катеты, а гипотенуза появляется только в синусе и косинусе.

А дальше можно придумать цепочку ассоциаций. К примеру, вот такую:

В первую очередь, необходимо запомнить, что синус, косинус, тангенс и котангенс как отношения сторон треугольника не зависят от длин этих сторон (при одном угле).

Тогда убедись, посмотрев на рисунок:

Рассмотрим, к примеру, косинус угла \( \beta \).

По определению, из треугольника \( ABC\): \( \cos \beta =\frac=\frac<4><6>=\frac<2><3>\).

Но ведь мы можем вычислить косинус угла \( \beta \) и из треугольника \( AHI\): \( \cos \beta =\frac=\frac<6><9>=\frac<2><3>\).

Видишь, длины у сторон разные, а значение косинуса одного угла одно и то же. Таким образом, значения синуса, косинуса, тангенса и котангенса зависят исключительно от величины угла.

Если разобрался в определениях, то вперёд закреплять их!

Тогда пробуй сам: посчитай то же самое для угла \( \beta \).

Ответы: \( \sin \ \beta =0,6;\ \cos \ \beta =0,8;\ tg\ \beta =0,75;\ ctg\ \beta =\frac<4><3>\).

Единичная (тригонометрическая) окружность

Разбираясь в понятиях градуса и радиана, мы рассматривали окружность с радиусом, равным \( 1\).

Такая окружность называется единичной. Еще ее называют тригонометрической. Это одно и тоже.

Эта окружность — универсальная шпаргалка для решения уравнений и даже неравенств, если уметь ей пользоваться!

У нас есть целая статья, посвященная ей, которая так и называется «Тригонометрическая (единичная) окружность».

Здесь мы тоже ее разберем довольно подробно.

Как можно заметить, данная окружность построена в декартовой системе координат.

Радиус окружности равен единице.

При этом центр окружности лежит в начале координат, начальное положение радиус-вектора зафиксировано вдоль положительного направления оси \( x\) (в нашем примере, это радиус \( AB\)).

Каждой точке окружности соответствуют два числа: координата по оси \( x\) и координата по оси \( y\).

А что это за числа-координаты? И вообще, какое отношение они имеют к рассматриваемой теме?

Для этого надо вспомнить про рассмотренный прямоугольный треугольник.

На рисунке, приведённом выше, можно заметить целых два прямоугольных треугольника.

Рассмотрим треугольник \( ACG\). Он прямоугольный, так как \( CG\) является перпендикуляром к оси \( x\).

Чему равен \( \cos \ \alpha \) из треугольника \( ACG\)?

Всё верно \( \cos \ \alpha =\frac\).

Кроме того, нам ведь известно, что \( AC\) – это радиус единичной окружности, а значит, \( AC=1\).

Подставим это значение в нашу формулу для косинуса. Вот что получается:

А чему равен \( \sin \ \alpha \) из треугольника \( ACG\)?

Ну конечно, \( \sin \alpha =\frac\)!

Подставим значение радиуса \( AC\) в эту формулу и получим:

Так, а можешь сказать, какие координаты имеет точка \( C\), принадлежащая окружности? Ну что, никак?

А если сообразить, что \( \cos \ \alpha \) и \( \sin \alpha \) — это просто числа?

Какой координате соответствует \( \cos \alpha \)?

Ну, конечно, координате \( x\)!

А какой координате соответствует \( \sin \alpha \)?

Всё верно, координате \( y\)!

Таким образом, точка \( C(x;y)=C(\cos \alpha ;\sin \alpha )\).

А чему тогда равны \( tg \alpha \) и \( ctg \alpha \)?

Всё верно, воспользуемся соответствующими определениями тангенса и котангенса и получим, что \( tg \alpha =\frac<\sin \alpha ><\cos \alpha >=\frac\), а \( ctg \alpha =\frac<\cos \alpha ><\sin \alpha >=\frac\).

А что, если угол будет больше \( 90<>^\circ =\frac<\pi ><2>\)?

Вот, к примеру, как на этом рисунке:

Что же изменилось в данном примере?

Давай разбираться. Для этого опять обратимся к прямоугольному треугольнику.

Всё верно, придерживаемся соответствующих определений тригонометрических функций:

Ну вот, как видишь, значение синуса угла всё так же соответствует координате \( y\); значение косинуса угла – координате \( x\); а значения тангенса и котангенса соответствующим соотношениям.

Таким образом, эти соотношения применимы к любым поворотам радиус-вектора.

Уже упоминалось, что начальное положение радиус-вектора – вдоль положительного направления оси \( x\).

До сих пор мы вращали этот вектор против часовой стрелки, а что будет, если повернуть его по часовой стрелке?

Ничего экстраординарного, получится так же угол определённой величины, но только он будет отрицательным.

Таким образом, при вращении радиус-вектора против часовой стрелки получаются положительные углы, а при вращении по часовой стрелке – отрицательные.

Итак, мы знаем, что целый оборот радиус-вектора по окружности составляет \( 360<>^\circ \) или \( 2\pi \).

В первом случае, \( 390<>^\circ =360<>^\circ +30<>^\circ \), таким образом, радиус-вектор совершит один полный оборот и остановится в положении \( 30<>^\circ \) или \( \frac<\pi ><6>\).

Таким образом, из приведённых примеров можем сделать вывод, что углы, отличающиеся на \( 360<>^\circ \cdot m\) или \( 2\pi \cdot m\) (где \( m\) – любое целое число), соответствуют одному и тому же положению радиус-вектора.

Ниже на рисунке изображён угол \( \beta =-60<>^\circ \).

Этот список можно продолжить до бесконечности.

Все эти углы можно записать общей формулой \( \beta +360<>^\circ \cdot m\) или \( \beta +2\pi \cdot m\) (где \( m\) – любое целое число)

Теперь, зная определения основных тригонометрических функций и используя единичную окружность, попробуй ответить, чему равны значения:

Вот тебе в помощь единичная окружность:

Возникли трудности? Тогда давай разбираться.

Отсюда мы определяем координаты точек, соответствующих определённым мерам угла.

Ну что же, начнём по порядку: углу в \( 90<>^\circ =\frac<\pi ><2>\) соответствует точка с координатами \( \left( 0;1 \right)\), следовательно:

\( \text\ 90<>^\circ =\frac=\frac<1><0>\Rightarrow \text\ 90<>^\circ \) — не существует;

Зная это, легко определить значения тригонометрических функций в соответствующих точках. Сначала попробуй сам, а потом сверяйся с ответами.

Ответы:

\( \displaystyle \sin \ 180<>^\circ =\sin \ \pi =0\) \( \displaystyle \cos \ 180<>^\circ =\cos \ \pi =-1\) \( \text\ 180<>^\circ =\text\ \pi =\frac<0><-1>=0\)

\( \text\ 180<>^\circ =\text\ \pi =\frac<-1><0>\Rightarrow \text\ \pi \) — не существует

\( \sin \ 270<>^\circ =-1\) \( \cos \ 270<>^\circ =0\)

\( \text\ 270<>^\circ =\frac<-1><0>\Rightarrow \text\ 270<>^\circ \) — не существует

\( \text\ 270<>^\circ =\frac<0><-1>=0\) \( \sin \ 360<>^\circ =0\) \( \cos \ 360<>^\circ =1\) \( \text\ 360<>^\circ =\frac<0><1>=0\)

\( \text\ 360<>^\circ =\frac<1><0>\Rightarrow \text\ 2\pi \) — не существует

\( \sin \ 450<>^\circ =\sin \ \left( 360<>^\circ +90<>^\circ \right)=\sin \ 90<>^\circ =1\) \( \cos \ 450<>^\circ =\cos \ \left( 360<>^\circ +90<>^\circ \right)=\cos \ 90<>^\circ =0\)

\( \text\ 450<>^\circ =\text\ \left( 360<>^\circ +90<>^\circ \right)=\text\ 90<>^\circ =\frac<1><0>\Rightarrow \text\ 450<>^\circ \) — не существует

\( \text\ 450<>^\circ =\text\left( 360<>^\circ +90<>^\circ \right)=\text\ 90<>^\circ =\frac<0><1>=0\).

Таким образом, мы можем составить следующую табличку:

Нет необходимости помнить все эти значения!

Достаточно помнить соответствие координат точек на единичной окружности и значений тригонометрических функций:

А вот значения тригонометрических функций углов в \( 30<>^\circ =\frac<\pi ><6>,\ 45<>^\circ =\frac<\pi ><4>\) и \( 30<>^\circ =\frac<\pi ><6>,\ 45<>^\circ =\frac<\pi ><4>\), приведённых ниже в таблице, необходимо запомнить:

Не надо пугаться, сейчас покажем один из примеров довольно простого запоминания соответствующих значений:

Источник

Алгебра

Лучшие условия по продуктам Тинькофф по этой ссылке

Дарим 500 ₽ на баланс сим-карты и 1000 ₽ при сохранении номера

. 500 руб. на счет при заказе сим-карты по этой ссылке

Лучшие условия по продуктам
ТИНЬКОФФ по данной ссылке

План урока:

Синус и косинус угла на единичной окружности

Впервые мы познакомились с синусом, косинусом и другими тригонометрическими функциями ещё в 8 класс на уроках геометрии, при изучении прямоугольного треугольника. Пусть есть некоторый треуг-ник АВС, у которого∠ С – прямой, а ∠ВАС принимается за α. Тогда sinα – это отношение ВС к АВ, а cosα– это отношение АС к АВ. В свою очередь tgα– это отношение ВС к АС:

С помощью тригонометрических функций удобно было находить стороны прямоугольного треугол-ка. Например, пусть известно, что гипотенуза АВ равна 5, а sinα = 0,8. Тогда из формулы sinα = ВС/АВ легко получить, что

ВС = АВ•sinα = 5•0,8 = 4

Если известно, что cosα = 0,6, то мы сможем найти и второй катет:

АС = АВ•cosα = 5•0,6 = 3

Отдельно заметим, что тангенс угла может быть рассчитан не как отношение двух катетов, а как отношение синуса к косинусу:

tgα = ВС/ АС = (АВ•sinα)/(АВ•cosα) = (sinα)/(cosα)

Отметим на единичной окружности произвольную точку А, которой соответствует некоторый угол α. У этой точки есть свои координаты х_А и у_А:

Попытаемся определить, чему равны координаты точки А. Для этого обозначим буквой B точку, в которой перпендикуляр, опущенный из А, пересекает горизонтальную ось Ох, и рассмотрим треугольник ОАВ:

Ясно, что ОАВ – это прямоугольный треугольник, ведь∠ АОВ = 90°. Значит, отрезок АВ можно рассчитать по формуле

Но ОА – это радиус единичной окружности. Это значит, что ОА = 1. Тогда

АВ = sinα•ОА = sinα•1 = sinα

С другой стороны, видно, что величина отрезка АВ равна координате у_А. Получается, что у_А = АВ = sinα, или

Отрезок ОВ также можно найти из прямоугольного треугольника АОВ, используя косинус:

Учитывая, что ОА = 1, а длина ОВ равна координате х_А, мы получим следующее:

х_А = ОВ = cosα•ОА = cosα•1 = cosα

то есть координата х_А равна cos α:

Итак, мы выяснили, что координаты точки, лежащей на единичной окружности, равны синусу и косинусу угла, соответствующего этой точке.

Таким образом, нам удалось дать новое определение синусу и косинусу угла:

Заметим, что в прямоугольном треугольнике углы, помимо самого прямого угла, могут быть только острыми. Поэтому предыдущее определение синуса и косинуса, данное в 8 классе в курсе геометрии, было пригодно лишь для углов из диапазона 0 1 I и II четверть

Источник

Начальные сведения о синусе, косинусе, тангенсе и котангенсе

Определения

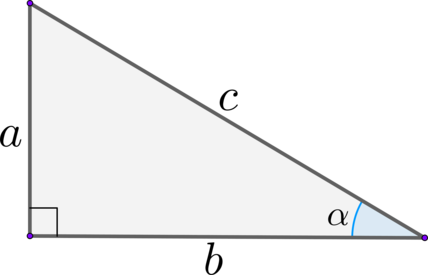
Синус острого угла в прямоугольном треугольнике – это отношение противолежащего к этому углу катета к гипотенузе: \(\sin \alpha=\dfrac ac\)

Косинус острого угла в прямоугольном треугольнике – это отношение прилежащего к этому углу катета к гипотенузе: \(\cos \alpha=\dfrac bc\)

Тангенс острого угла в прямоугольном треугольнике – это отношение противолежащего к этому углу катета к прилежащему катету: \(\mathrm\,\alpha=\dfrac ab\)

Котангенс острого угла в прямоугольном треугольнике – это отношение прилежащего к этому углу катета к противолежащему катету: \(\mathrm\,\alpha=\dfrac ba\)

Утверждение

Синусы, косинусы, тангенсы и котангенсы равных углов соответственно равны.

Теорема

Из определений синуса, косинуса, тангенса и котангенса вытекают следующие формулы:

Утверждение

В прямоугольном треугольнике \(ABC\) с прямым углом \(\angle C\) :

\(\sin \angle A=\cos \angle B\)

Доказательство

Утверждение следует непосредственно из определения синуса и косинуса острого угла в прямоугольном треугольнике.

Теорема

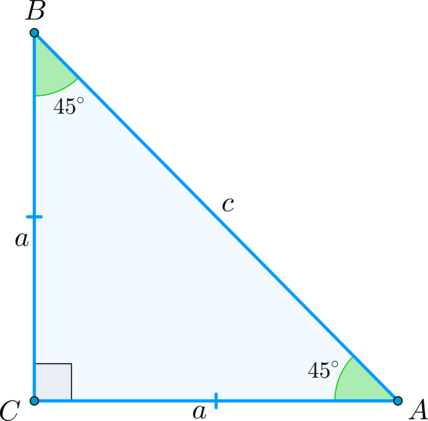
Для углов \(30^\circ, 45^\circ, 60^\circ\) верна следующая таблица:

\[<\large<\begin <|c|c|c|c|>\hline & \phantom<000>30^\circ \phantom <000>& \phantom <000>45^\circ \phantom <000>& \phantom <000>60^\circ \phantom <000>\\[2pt] \hline &&&\\ \sin &\frac12&\frac<\sqrt2>2&\frac<\sqrt3>2\\[4pt] \cos &\frac<\sqrt3>2&\frac<\sqrt2>2&\frac12\\[4pt] \mathrm &\frac<\sqrt3>3&1&\sqrt3\\[4pt] \mathrm&\sqrt3&1&\frac<\sqrt3>3\\[4pt] \hline \end>>\]

Доказательство

Теперь по определению \(\sin \angle A=\sin 60^\circ =\dfrac ac=\dfrac<\sqrt3>2\)

Замечание

Для простоты запоминания таблицы можно записать ее в следующем виде:

Теорема

Справедливы следующие формулы приведения:

\[\begin \sin(180^\circ-\alpha)&=\sin\alpha\\ \cos(180^\circ-\alpha)&=-\cos\alpha\\ \mathrm\,(180^\circ-\alpha)&=-\mathrm\,\alpha\\ \mathrm\,(180^\circ-\alpha)&=-\mathrm\,\alpha \end\]

Пример

Учащиеся, которые готовятся к сдаче ЕГЭ по математике и при этом рассчитывают на получение конкурентных баллов по итогам его прохождения, непременно должны повторить теорию о синусе, косинусе, тангенсе и котангенсе. Как показывает практика, задания по данной тематике ежегодно встречаются в аттестационном испытании. Таким образом, если одним из ваших слабых мест являются формулы и теоремы синусов, косинусов, тангенсов и котангенсов, рекомендуем освежить в памяти базовую теорию. В этом вам поможет образовательный портал «Школково». В соответствующем разделе представлена теория о синусах, косинусах, тангенсах и котангенсах, которая позволит вам подготовиться к сдаче экзамена. Весь базовый материал составлен нашими специалистами на основе многолетнего опыта и представлен в максимально доступной форме. Ознакомившись с теорией, выпускник сможет грамотно объяснять решение задач ЕГЭ на синусы, косинусы, тангенсы и котангенсы. В этом состоит половина успеха при прохождении аттестационного испытания.

Для того чтобы учащиеся из Москвы или другого населенного пункта России, посетившие наш ресурс, смогли легко и качественно подготовиться к ЕГЭ, мы не только в понятной форме изложили теорию косинусов, синусов, тангенсов и котангенсов, но и подобрали соответствующие упражнения. Для каждого из них наши специалисты прописали подробный алгоритм решения и правильный ответ. Выполняя такие задачи при подготовке к ЕГЭ по математике, выпускники смогут лучше закрепить изученную теорию синусов и косинусов в треугольнике. Выбрать простые и более сложные упражнения вы можете в разделе «Каталог».

Изучив теорию о синусах, косинусах, тангенсах и котангенсах и попрактиковавшись в решении задач по данной теме при подготовке к ЕГЭ, учащиеся имеют возможность сохранить любое задание в «Избранное», чтобы при необходимости обсудить его с преподавателем.

Источник

Что такое синус, косинус, тангенс и котангенс в прямоугольном треугольнике?

Синус, косинус и тангенс острого угла прямоугольного треугольника.

Приветствую Вас дорогие учащиеся.

Сейчас рассмотрим что же такое синус, косинус, тангенс и котангенс в прямоугольном треугольнике?

Это тема не сложная, главное это запомнить правила. И так начнем:

Вспомним, что такое прямоугольный треугольник?

Прямоугольным треугольником, называется треугольник у которого один из углов прямой (составляет 90 градусов). Две стороны которые прилежат к прямому углу, называются катетами, а сторона лежащая напротив прямого угла, называется гипотенузой.

Синус (sin(a)) — это отношение противолежащего катета к гипотенузе;

Косинус (cos(a)) — это отношение прилежащего катета к гипотенузе;

Тангенс (tg(a)) — это отношение противолежащего катета к прилежащему катету;
Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу;

Котангенс (ctg(a)) — это отношение прилежащего катета к противолежащему.
Другое (равносильное) определение: котангенсом острого угла называется отношение косинуса угла к его синусу;

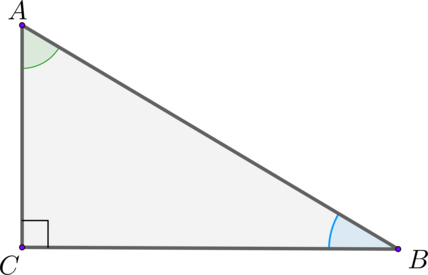
Пусть дан прямоугольный треугольник ABC с прямым углом C.

Найти sin(a); cos(a); tg(a); ctg(a) Отношение сторон в прямоугольном треугольнике

Аналогично рассуждаем относительно угла B.

Найти sin(b); cos(b); tg(b); ctg(b) Отношение сторон в прямоугольном треугольнике

Пример:

Найти тангенс угла С (tg(C)) треугольника ABC.

Хочешь готовиться к экзаменам бесплатно? Репетитор онлайн бесплатно. Без шуток. ЗДЕСЬ

Источник