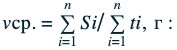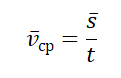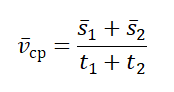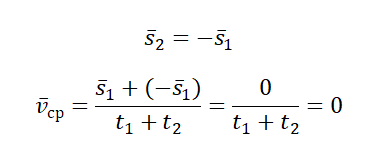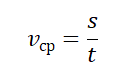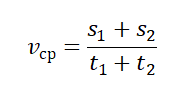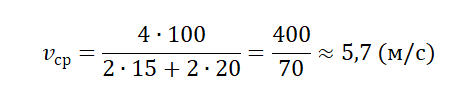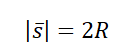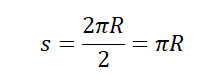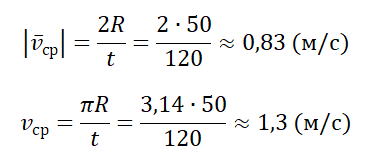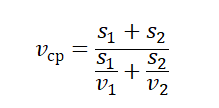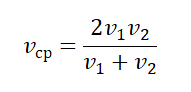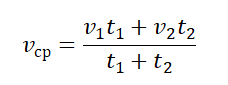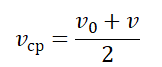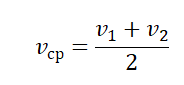Как находить среднюю скорость формула
Вычисление средней скорости движения в физике: расчёты и формулы
Содержание:
Под средней скоростью движения какого-либо тела понимают отношение пройденного расстояния к временному промежутку, который был затрачен на его преодоление. Определение средней скорости может понадобиться в случае, когда в процессе перемещения тела на разных участках его скорость изменялась. Неважно в каком направлении совершалось движение и изменялось ли оно с течением времени. Характер движения может быть сложным или простым. Средняя скорость является скалярной величиной, поэтому алгоритм вычисления всегда будет примерно одинаковым.
Как найти среднюю скорость тела?
Пример. Автомобиль всего проехал 1 километр и 200 метров. После каждых 400 м он изменял скорость движения. Первые 400 метров он двигался со скоростью 20 км/ч, потом со скоростью 40 км/ч, 50 км/ч и последний участок проехал на скорости 35 км/ч. Определение средней скорости движения производим так:
В любом другом случае вычисление средней скорости в физике производят более сложным путем по формуле:
Пример задачи на вычисление средней скорости в физике
Сначала найдем путь, который был пройден за каждый из промежутков времени:
Далее пишется вышеприведенная формула в более привычном виде, как обычно, подставляются необходимые данные и определяется средняя скорость:
Средняя скорость при равноускоренном движении
На практике очень часто встречаются задачи, когда вычисление средней скорости необходимо производить для случая, когда тело, двигаясь с какой-то начальной скоростью, с течением времени начало ускоряться и в конце пути достигло какой-то новой скорости. Тогда следует использовать формулу, которая выражает среднюю скорость через величину ускорения:
vcp. = v0 + \frac < at > < 2 >, где:
Пример. Двигаясь с начальной скоростью 160 м/с, самолет в течение двух минут ускорял свое движение на 1,5 м/с2. Какова его средняя скорость за этот промежуток времени?
vcp. = 160 + \frac < 1,5 * 120 > < 2 >= 250 м/с
Способы нахождения средней скорости в физике
Основные понятия и законы кинематики
Кинематика — раздел механики, описывающий механическое движение тел без рассмотрения причин, из-за которых происходит движение.
Механическое движение — это изменение положения тела в пространстве относительно других тел с течением времени.
Для описания движения нужна система отсчета, относительно которой мы будем описывать движение.
Система отсчета — это система координат, связанная с телом отсчета и прибор для измерения времени.
Тело отсчета — это тело, относительно которого рассматривают положение других тел.
Материальная точка — это тело, размеры которого можно не учитывать при решении задачи.
Траектория — это мысленная линия в пространстве, которую при движении описывает материальная точка.
Траектория движения делится на два типа:
Путь — это длина траектории, которую описывает тело или материальная точка за данный промежуток времени.
Перемещение S → — это вектор, соединяющий начальное положение тела или материальной точки с ее конечным положением.
Скорость — это векторная физическая величина, характеризующаяся направлением и быстротой перемещения материальной точки.
Определение средней скорости
Рассчитать среднюю скорость можно по следующей формуле:
Определение средней путевой скорости
Средняя путевая скорость — это отношение пути или длины траектории, пройденного телом, к интервалу времени, за которое этот путь был пройден.
Формула средней путевой скорости выглядит так:
Примеры решения задач
Автомобиль первый час ехал со скоростью 100 км/ч, после чего сделал остановку. Следующие два часа автомобиль ехал со скоростью 90 км/ч, а затем два часа — со скоростью 80 км/ч. Найдите среднюю скорость на протяжении всего пути автомобиля.
В условии сказано о трех участках пути.
ϑ с р → = S 1 → + S 2 → + S 3 → t 1 + t 2 + t 3
Участки пути мы можем вычислить и посчитать следующим образом:
Первый участок пути составил 1∙100 = 100 километров.
Второй участок пути составил 2∙90 = 180 километров.
Третий участок пути составил 2∙80 = 160 километров.
ϑ с р = 100 + 180 + 160 1 + 2 + 2 = 440 5 = 88 к м ч
Ответ: средняя скорость составляет 88 км/ч.
Автомобиль проехал по дороге расстояние 140 км за время, равное 2 часам, затем сделал остановку. После остановки автомобиль проехал 60 км за 3 часа. Какова средняя скорость автомобиля за весь путь?
ϑ с р → = ∆ S → ∆ t ϑ с р → = S 1 → + S 2 → t 1 + t 2 ϑ с р → = 140 + 60 2 + 3 = 40 к м ч
Ответ: средняя скорость автомобиля составляет 40 км/ч.
Человек занимается бегом и за 2 часа пробежал 5 км, а за следующий час пробежал 3 км. Определите среднюю скорость бегуна.
Искать среднюю скорость будем как во второй задаче.
Неравномерное движение и средняя скорость
теория по физике 🧲 кинематика
Неравномерное движение — движение с переменной скоростью, которая может менять как направление, так и модуль.
Неравномерное движение можно охарактеризовать средней скоростью. Различают среднюю векторную и среднюю скалярную скорости.
Средняя векторная скорость
Средняя векторная скорость — это скорость, равная отношению перемещения тела ко времени, в течение которого это перемещение было совершено.
v ср — средняя векторная скорость, s — перемещение тела, совершенное за время t
Направление вектора средней скорости всегда совпадает с направлением вектора перемещения.
Чтобы вычислить среднюю векторную скорость, нужно поделить сумму всех перемещений на сумму всех временных промежутков, в течение которых эти перемещения были совершены:
Пример №1. Миша пробежал стометровку за 16 секунд. Через 1 минуту он вернулся на старт. Найти среднюю векторную скорость мальчика.
Миша совершил одинаковые по модулю, но разные по направлению перемещения. При сложении этих векторов получается 0. Поэтому средняя векторная скорость также равна нулю:
Средняя скалярная скорость
Средняя скалярная (путевая) скорость — это скорость, равная отношению пути, пройденного телом, ко времени, в течение которого этот путь был пройден.
vср — средняя путевая скорость, s — путь, пройденный телом за время t
Чтобы вычислить среднюю путевую скорость, нужно поделить сумму всех путей на сумму всех временных промежутков, в течение которых эти пути были преодолены:
Пример №2. Мальчик пробежал по периметру квадратного поля сто стороной 100 м. На первые две стороны мальчик потратил по 15 секунд, а на последние две — по 20 секунд. Найти среднюю путевую скорость мальчика.
У квадрата 4 стороны, поэтому путь мальчика составляют 4 дистанции по 100 м каждая. Поэтому средняя путевая скорость равна:
Средняя скалярная скорость всегда больше или равна модулю средней векторной скорости:
Пример №3. Рыболов остановился на берегу круглого пруда и увидел на противоположном берегу удобное для рыбалки место. Он к нему шел в течение 2 минут. Вычислите среднюю путевую и среднюю векторную скорости рыболова после того, как он придет на новое место, если радиус пруда равен 50 м.
Две противоположные точки окружности соединяются отрезком, проходящим через его центр — диаметром. Поэтому модуль вектора перемещения равен двум радиусам пруда:
Чтобы дойти до диаметрально противоположной точки окружности, нужно пройти путь, равный половине окружности:
Переведя 2 минуты в СИ, получим 120 с. Модуль средней векторно скорости равен:
Пример №4. Первые полчаса автомобиль двигался со скоростью 90 км/ч, а потом 1 час он двигался со скоростью 60 км/ч. Найти среднюю скорость автомобиля.
Нам известны скорости на каждом из участков пути и время, в течение которого каждый из этих участков был преодолен. Поэтому:
Виды скорости в физике и методы их вычисления
Скорость в физике — что это такое
Скорость — векторная физическая величина, которая характеризуется направлением и быстротой перемещения материальной точки.
В физике понятие скорости встречается в разделе «Кинематика», в котором дается описание механического движения, а это основа изучения скорости как векторной физической величины.
Скорость может характеризоваться быстротой перемещения не только материальной точки, но и еще элементарных частиц и волн.
Скорость звука — это величина, которая показывает, на какое расстояние может распространиться звуковая волна за единицу времени.
Скорость света — абсолютная величина, которая показывает скорость распространения электромагнитных волн.
Виды скорости в физике, основные характеристики
В физике существуют такие виды скорости, как: начальная скорость, равномерная скорость, средняя скорость, мгновенная скорость.
Как писалось выше, скорость равна отношению пути S ко времени t.
Формулы скорости при движении разных видов
ϑ н — начальная скорость;
ϑ 0 — конечная скорость;
Примеры задач с решением
На автомобиле за 3 часа проехали 180 км с одной и той же скоростью. Чему равна скорость автомобиля?
Решение:
Скорость — это расстояние, пройденное телом за единицу времени. Чтобы определить скорость, нужно пройденное расстояние разделить на время движения.
Если за 3 часа автомобиль проехал 180 километров с одной и той же скоростью, то разделив 180 км на 3 часа мы определим расстояние, которое проезжал автомобиль за один час. А это и есть скорость движения.
ϑ = 180 3 = 60 к м ч
Ответ: скорость автомобиля составляет 60 км/ч.
Первый час автомобиль ехал со скоростью 100 км/ч, следующие два часа — со скоростью 90 км/ч, а затем два часа — со скоростью 80 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
В условии сказано о трех участках пути.
ϑ с р = S о б щ t о б щ
ϑ с р = S 1 + S 2 + S 3 t 1 + t 2 + t 3
Участки пути нам не даны, но мы можем без труда их вычислить:
Первый участок пути составил 1∙100 = 100 километров.
Второй участок пути составил 2∙90 = 180 километров.
Третий участок пути составил 2∙80 = 160 километров.
ϑ с р = 100 + 180 + 160 1 + 2 + 2 / = 440 5 = 88 к м ч
Ответ: средняя скорость составляет 88 км/ч.
Конечная скорость после 2 секунд движения с ускорением 0,2 м/с², равна 3 м/с. Найти начальную скорость.
Ответ: начальная скорость составляет 2,6 м/с.
Как найти скорость зная среднюю скорость
В создании этой статьи участвовала наша опытная команда редакторов и исследователей, которые проверили ее на точность и полноту.
Количество источников, использованных в этой статье: 8. Вы найдете их список внизу страницы.
Команда контент-менеджеров wikiHow тщательно следит за работой редакторов, чтобы гарантировать соответствие каждой статьи нашим высоким стандартам качества.
Чтобы вычислить среднюю скорость, воспользуйтесь простой формулой: Скорость = Пройденный путь Время >= > >>> 
. Но в некоторых задачах даются два значения скорости — на разных участках пройденного пути или в различные промежутки времени. В этих случаях нужно пользоваться другими формулами для вычисления средней скорости. Навыки решения подобных задач могут пригодиться в реальной жизни, а сами задачи могут встретиться на экзаменах, поэтому запомните формулы и уясните принципы решения задач.
На данной странице калькулятор поможет рассчитать среднюю скорость онлайн. Для расчета задайте расстояние и время.
Средняя (путевая) скорость — это отношение длины пути, пройденного телом, ко времени, за которое этот путь был пройден.
Через расстояние и время
Формула для нахождения средней скорости, зная расстояние и время:
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
На прошлых уроках мы рассматривали равномерное движение. На этом уроке будет рассмотрено движение с изменяющейся скоростью, то есть неравномерное движение. Также мы выучим характеристики неравномерного движения – среднюю скорость и мгновенную скорость.
Введение
Рассмотрим некоторые виды движения:
— колебание груза на пружинном маятнике (рис. 1);
Рис. 1. Колебание груза на пружинном маятнике (Источник)
— скатывание тела по наклонной плоскости (рис. 2);
Рис. 2. Скатывание тела по наклонной плоскости (Источник)
— свободное падение (рис. 3).
Рис. 3. Свободное падение (Источник)
Все эти три вида движения не являются равномерными, то есть в них изменяется скорость. На этом уроке мы рассмотрим неравномерное движение.
Неравномерное движение
Равномерное движение – механическое движение, при котором тело за любые равные отрезки времени проходит одинаковое расстояние (рис. 4).
Рис. 4. Равномерное движение
Неравномерным называется движение, при котором тело за равные промежутки времени проходит неравные пути.
Рис. 5. Неравномерное движение
Основная задача механики – определить положение тела в любой момент времени. При неравномерном движении скорость тела меняется, следовательно, необходимо научиться описывать изменение скорости тела. Для этого вводятся два понятия: средняя скорость и мгновенная скорость.
Средняя скорость
Факт изменения скорости тела при неравномерном движении не всегда необходимо учитывать, при рассмотрении движении тела на большом участке пути в целом (нам не важна скорость в каждый момент времени) удобно ввести понятие средней скорости.
Например, делегация школьников добирается из Новосибирска в Сочи поездом. Расстояние между этими городами по железной дороге составляет приблизительно 3300 км. Скорость поезда, когда он только выехал из Новосибирска составляла (рис. 6). Конечно нет, так как жители Новосибирска знают, что до Сочи ехать приблизительно 84 ч.
Рис. 6. Иллюстрация к примеру
Когда рассматривается движение тела на большом участке пути в целом, удобнее ввести понятие средней скорости.
Средней скоростью называют отношение полного перемещения, которое совершило тело, ко времени, за которое совершено это перемещение (рис. 7).
Рис. 7. Средняя скорость
Данное определение не всегда является удобным. Например, спортсмен пробегает 400 м – ровно один круг. Перемещение спортсмена равно 0 (рис. 8), однако мы понимаем, что его средняя скорость нулю равна быть не может.
Рис. 8. Перемещение равно 0
На практике чаще всего используется понятие средней путевой скорости.
Средняя путевая скорость – это отношение полного пути, пройденного телом, ко времени, за которое путь пройден (рис. 9).
Рис. 9. Средняя путевая скорость
Существует еще одно определение средней скорости.
Средняя скорость – это та скорость, с которой должно двигаться тело равномерно, чтобы пройти данное расстояние за то же время, за которое оно его прошло, двигаясь неравномерно.
Из курса математики нам известно, что такое среднее арифметическое. Для чисел 10 и 36 оно будет равно:
Для того чтобы узнать возможность использования этой формулы для нахождения средней скорости, решим следующую задачу.
Велосипедист поднимается со скоростью 10 км/ч на склон, затрачивая на это 0,5 часа. Далее со скоростью 36 км/ч спускается вниз за 10 минут. Найдите среднюю скорость велосипедиста (рис. 10).
Рис. 10. Иллюстрация к задаче
Дано:
Найти:
Так как единица измерения данных скоростей – км/ч, то и среднюю скорость найдем в км/ч. Следовательно, данные задачи не будем переводить в СИ. Переведем в часы.
Средняя скорость равна:
Полный путь ():
Путь подъема на склон равен:
Путь спуска со склона равен:
Время, за которое пройден полный путь, равно:
Ответ:.
Исходя из ответа задачи, видим, что применять формулу среднего арифметического для вычисления средней скорости нельзя.
Не всегда понятие средней скорости полезно для решения главной задачи механики. Возвращаясь к задаче про поезд, нельзя утверждать, что если средняя скорость на всем пути поезда равна от Новосибирска.
Мгновенная скорость
Среднюю скорость, измеренную за бесконечно малый промежуток времени, называют мгновенной скоростью тела (для примера: спидометр автомобиля (рис. 11) показывает мгновенную скорость).
Рис. 11. Спидометр автомобиля показывает мгновенную скорость
Существует еще одно определение мгновенной скорости.
Мгновенная скорость – скорость движения тела в данный момент времени, скорость тела в данной точке траектории (рис. 12).
Рис. 12. Мгновенная скорость
Для того чтобы лучше понять данное определение, рассмотрим пример.
Пусть автомобиль движется прямолинейно по участку шоссе. У нас есть график зависимости проекции перемещения от времени для данного движения (рис. 13), проанализируем данный график.
Рис. 13. График зависимости проекции перемещения от времени
На графике видно, что скорость автомобиля не постоянная. Допустим, необходимо найти мгновенную скорость автомобиля через 30 секунд после начала наблюдения (в точке A). Пользуясь определением мгновенной скорости, найдем модуль средней скорости за промежуток времени от . Для этого рассмотрим фрагмент данного графика (рис. 14).
Рис. 14. График зависимости проекции перемещения от времени
Рассчитываем среднюю скорость на данном участке времени:
Для того чтобы проверить правильность нахождения мгновенной скорости, найдем модуль средней скорости за промежуток времени от , для этого рассмотрим фрагмент графика (рис. 15).
Рис. 15. График зависимости проекции перемещения от времени
Рассчитываем среднюю скорость на данном участке времени:
Получили два значения мгновенной скорости автомобиля через 30 секунд после начала наблюдения. Точнее будет то значение, где интервал времени меньше, то есть . Если уменьшать рассматриваемый интервал времени сильнее, то мгновенная скорость автомобиля в точке A будет определяться более точно.
Мгновенная скорость – это векторная величина. Поэтому, кроме ее нахождения (нахождения ее модуля), необходимо знать, как она направлена.
) – мгновенная скорость
Направление мгновенной скорости совпадает с направлением перемещения тела.
Если тело движется криволинейно, то мгновенная скорость направлена по касательной к траектории в данной точке (рис. 16).
Рис. 16. Направление мгновенной скорости
Задания для усвоения понятия «мгновенная скорость»
Может ли мгновенная скорость () изменяться только по направлению, не изменяясь по модулю?
Для решения рассмотрим следующий пример. Тело движется по криволинейной траектории (рис. 17). Отметим на траектории движения точку A и точку B. Отметим направление мгновенной скорости в этих точках (мгновенная скорость направлена по касательной к точке траектории). Пусть скорости одинаковы по модулю и равны 5 м/с.
Рис. 17. Иллюстрация к задаче
Написать, что нельзя. Скорость – векторная величина, то есть важно не только числовое значение, но и направление.
Если бы , то есть мгновенная скорость может быть равна по модулю, но отличаться по направлению.
Может ли мгновенная скорость меняться только по модулю, не меняясь по направлению?
Рис. 18. Иллюстрация к задаче
На рисунке 10 видно, что в точке A и в точке B мгновенная скорость направлена одинаково. Если тело движется равноускоренно, то .
Итоги урока
На данном уроке мы приступили к изучению неравномерного движения, то есть движения с изменяющейся скоростью. Характеристиками неравномерного движения являются средняя и мгновенная скорости. Понятие о средней скорости основано на мысленной замене неравномерного движения равномерным. Иногда понятие средней скорости (как мы увидели) является очень удобным, но для решения главной задачи механики оно не подходит. Поэтому вводится понятие мгновенной скорости.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта.