Как находить точку пересечения прямых

При решении некоторых геометрических задач методом координат приходится находить координаты точки пересечения прямых. Наиболее часто приходится искать координаты точки пересечения двух прямых на плоскости, однако иногда возникает необходимость в определении координат точки пересечения двух прямых в пространстве. В этой статье мы как раз разберемся с нахождением координат точки, в которой пересекаются две прямые.

Навигация по странице.

Точка пересечения двух прямых – определение.

Давайте для начала дадим определение точки пересечения двух прямых.

В разделе взаимное расположение прямых на плоскости показано, что две прямые на плоскости могут либо совпадать (при этом они имеют бесконечно много общих точек), либо быть параллельными (при этом две прямые не имеют общих точек), либо пересекаться, имея одну общую точку. Вариантов взаимного расположения двух прямых в пространстве больше – они могут совпадать (иметь бесконечно много общих точек), могут быть параллельными (то есть, лежать в одной плоскости и не пересекаться), могут быть скрещивающимися (не лежащими в одной плоскости), а также могут иметь одну общую точку, то есть, пересекаться. Итак, две прямые и на плоскости и в пространстве называются пересекающимися, если они имеют одну общую точку.

Из определения пересекающихся прямых следует определение точки пересечения прямых: точка, в которой пересекаются две прямые, называется точкой пересечения этих прямых. Другими словами, единственная общая точка двух пересекающихся прямых есть точка пересечения этих прямых.

Приведем для наглядности графическую иллюстрацию точки пересечения двух прямых на плоскости и в пространстве.

Нахождение координат точки пересечения двух прямых на плоскости.

Прежде чем находить координаты точки пересечения двух прямых на плоскости по их известным уравнениям, рассмотрим вспомогательную задачу.

Решим поставленную задачу.

Если М₀ действительно точка пересечения заданных прямых, то ее координаты удовлетворяют уравнениям прямых. Проверим это, подставив координаты точки М₀ в заданные уравнения:

Для наглядности приведем чертеж, на котором изображены прямые и видны координаты точки их пересечения.

Подставим координаты точки М₀ в уравнения прямых, этим действием будем осуществлена проверка принадлежности точки М₀ обеим прямым одновременно:

Теперь можно переходить к задаче нахождения координат точки пересечения двух прямых по заданным уравнениям прямых на плоскости.

Пусть на плоскости зафиксирована прямоугольная декартова система координат Oxy и заданы две пересекающиеся прямые a и b уравнениями и соответственно. Обозначим точку пересечения заданных прямых как М₀ и решим следующую задачу: найти координаты точки пересечения двух прямых a и b по известным уравнениям этих прямых и .

Точка M₀ принадлежит каждой из пересекающихся прямых a и b по определению. Тогда координаты точки пересечения прямых a и b удовлетворяют одновременно и уравнению и уравнению . Следовательно, координаты точки пересечения двух прямых a и b являются решением системы уравнений (смотрите статью решение систем линейных алгебраических уравнений).

Таким образом, чтобы найти координаты точки пересечения двух прямых, определенных на плоскости общими уравнениями, нужно решить систему, составленную из уравнений заданных прямых.

Рассмотрим решение примера.

Нам даны два общих уравнения прямых, составим из них систему: . Решения полученной системы уравнений легко находятся, если разрешить ее первое уравнение относительно переменной x и подставить это выражение во второе уравнение:

Найденное решение системы уравнений дает нам искомые координаты точки пересечения двух прямых.

Итак, нахождение координат точки пересечения двух прямых, определенных общими уравнениями на плоскости, сводится к решению системы из двух линейных уравнений с двумя неизвестными переменными. А как же быть, если прямые на плоскости заданы не общими уравнениями, а уравнениями другого вида (смотрите виды уравнения прямой на плоскости)? В этих случаях можно сначала привести уравнения прямых к общему виду, а уже после этого находить координаты точки пересечения.

Определите координаты точки пересечения прямых и .

Перед нахождением координат точки пересечения заданных прямых приведем их уравнения к общему виду. Переход от параметрических уравнений прямой к общему уравнению этой прямой выглядит следующим образом:

Теперь проведем необходимые действия с каноническим уравнением прямой :

Таким образом, искомые координаты точки пересечения прямых являются решением системы уравнений вида . Используем для ее решения метод Крамера:

Существует еще один способ нахождения координат точки пересечения двух прямых на плоскости. Его удобно применять, когда одна из прямых задана параметрическими уравнениями вида , а другая – уравнением прямой иного вида. В этом случае в другое уравнение вместо переменных x и y можно подставить выражения и , откуда можно будет получить значение , которое соответствует точке пересечения заданных прямых. При этом точка пересечения прямых имеет координаты .

Найдем координаты точки пересечения прямых из предыдущего примера этим способом.

Определите координаты точки пересечения прямых и .

Подставим в уравнение прямой выражения :

Решив полученное уравнение, получаем . Это значение соответствует общей точке прямых и . Вычисляем координаты точки пересечения, подставив в параметрические уравнения прямой:
.

Для полноты картины следует обговорить еще один момент.

Перед нахождением координат точки пересечения двух прямых на плоскости полезно убедиться в том, что заданные прямые действительно пересекаются. Если выяснится, что исходные прямые совпадают или параллельны, то о нахождении координат точки пересечения таких прямых не может быть и речи.

Рассмотрим примеры, подходящие под эти ситуации.

Выясните, пересекаются ли прямые и , и если пересекаются, то найдите координаты точки пересечения.

Заданным уравнениям прямых соответствуют уравнения и . Решим систему, составленную из этих уравнений .

Очевидно, что уравнения системы линейно выражаются друг через друга (второе уравнение системы получается из первого умножением обеих его частей на 4 ), следовательно, система уравнений имеет бесконечное множество решений. Таким образом, уравнения и определяют одну и ту же прямую, и мы не можем говорить о нахождении координат точки пересечения этих прямых.

уравнения и определяют в прямоугольной системе координат Oxy одну и ту же прямую, поэтому мы не можем говорить о нахождении координат точки пересечения.

Найдите координаты точки пересечения прямых и , если это возможно.

Условие задачи допускает, что прямые могут быть не пересекающимися. Составим систему из данных уравнений. Применим для ее решения метод Гаусса, так как он позволяет установить совместность или несовместность системы уравнений, а в случае ее совместности найти решение:

Последнее уравнение системы после прямого хода метода Гаусса обратилось в неверное равенство, следовательно, система уравнений не имеет решений. Отсюда можно сделать вывод, что исходные прямые параллельны, и мы не можем говорить о нахождении координат точки пересечения этих прямых.

Второй способ решения.

Давайте выясним, пересекаются ли заданные прямые.

— нормальный вектор прямой , а вектор является нормальным вектором прямой . Проверим выполнение условия коллинеарности векторов и : равенство верно, так как , следовательно, нормальные векторы заданных прямых коллинеарны. Тогда, эти прямые параллельны или совпадают. Таким образом, мы не можем найти координаты точки пересечения исходных прямых.

координаты точки пересечения заданных прямых найти невозможно, так как эти прямые параллельны.

Найдите координаты точки пересечения прямых 2x-1=0 и , если они пересекаются.

Составим систему из уравнений, которые являются общими уравнениями заданных прямых: . Определитель основной матрицы этой системы уравнений отличен от нуля , поэтому система уравнений имеет единственное решение, что свидетельствует о пересечении заданных прямых.

Для нахождения координат точки пересечения прямых нам нужно решить систему:

Полученное решение дает нам координаты точки пересечения прямых, то есть, — точка пересечения прямых 2x-1=0 и .

Нахождение координат точки пересечения двух прямых в пространстве.

Координаты точки пересечения двух прямых в трехмерном пространстве находятся аналогично.

Рассмотрим решения примеров.

Найдите координаты точки пересечения двух прямых, заданных в пространстве уравнениями и .

Составим систему уравнений из уравнений заданных прямых: . Решение этой системы даст нам искомые координаты точки пересечения прямых в пространстве. Найдем решение записанной системы уравнений.

Таким образом, ранг основной матрицы равен рангу расширенной матрицы и равен трем.

Следовательно, система уравнений имеет единственное решение.

Базисным минором примем определитель , поэтому из системы уравнений следует исключить последнее уравнение, так как оно не участвует в образовании базисного минора. Итак,

Решение полученной системы легко находится:

Следует отметить, что система уравнений имеет единственное решение тогда и только тогда, когда прямые a и b пересекаются. Если же прямые а и b параллельные или скрещивающиеся, то последняя система уравнений решений не имеет, так как в этом случае прямые не имеют общих точек. Если прямые a и b совпадают, то они имеют бесконечное множество общих точек, следовательно, указанная система уравнений имеет бесконечное множество решений. Однако в этих случаях мы не можем говорить о нахождении координат точки пересечения прямых, так как прямые не являются пересекающимися.

Можно обойтись и без использования метода Гаусса. Как вариант, можно вычислить ранги основной и расширенной матриц этой системы, и на основании полученных данных и теоремы Кронекера-Капелли сделать вывод или о существовании единственного решения, или о существовании множества решений, или об отсутствии решений. Это дело вкуса.

Если прямые и пересекаются, то определите координаты точки пересечения.

Составим систему из заданных уравнений: . Решим ее методом Гаусса в матричной форме:

Стало видно, что система уравнений не имеет решений, следовательно, заданные прямые не пересекаются, и не может быть и речи о поиске координат точки пересечения этих прямых.

мы не можем найти координаты точки пересечения заданных прямых, так как эти прямые не пересекаются.

Когда пересекающиеся прямые заданы каноническими уравнениями прямой в пространстве или параметрическими уравнениями прямой в пространстве, то следует сначала получить их уравнения в виде двух пересекающихся плоскостей, а уже после этого находить координаты точки пересечения.

Две пересекающиеся прямые заданы в прямоугольной системе координат Oxyz уравнениями и . Найдите координаты точки пересечения этих прямых.

Зададим исходные прямые уравнениями двух пересекающихся плоскостей:

Источник

Точка пересечения прямых в пространстве онлайн

С помощю этого онлайн калькулятора можно найти точку пересечения прямых в пространстве. Дается подробное решение с пояснениями. Для нахождения координат точки пересечения прямых задайте вид уравнения прямых («канонический» или «параметрический» ), введите коэффициенты уравнений прямых в ячейки и нажимайте на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.

Предупреждение

Точка пересечения прямых в пространстве − теория, примеры и решения

1. Точка пересечения прямых в пространстве, заданных в каноническом виде.

Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямые L₁ и L₂:

,

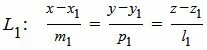(1)

,

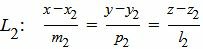(2)

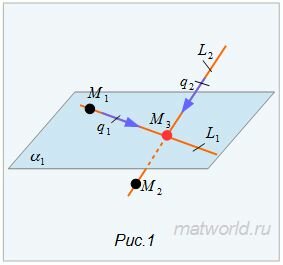
Найти точку пересечения прямых L₁ и L₂ (Рис.1).

Запишем уравнение (1) в виде системы двух линейных уравнений:

Сделаем перекрестное умножение в уравнениях (3) и (4):

Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:

Аналогичным образом преобразуем уравнение (2):

Запишем уравнение (2) в виде системы двух линейных уравнений:

Сделаем перекрестное умножение в уравнениях (7) и (8):

Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:

Решим систему линейных уравнений (5), (6), (9), (10) с тремя неизвестными x, y, z. Для этого представим эту систему в матричном виде:

2. Точка пересечения прямых в пространстве, заданных в параметрическом виде.

Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямые L₁ и L₂ в параметрическом виде:

Задачу нахождения нахождения точки пересечения прямых L₁ и L₂ можно решить разными методами.

Метод 1. Приведем уравнения прямых L₁ и L₂ к каноническому виду.

Для приведения уравнения (12) к каноническому виду, выразим параметр t через остальные переменные:

Так как левые части уравнений (14) равны, то можем записать:

Аналогичным образом приведем уравнение прямой L₂ к каноническому виду:

Далее, для нахождения точки пересечения прямых, заданных в каноническом виде нужно воспользоваться параграфом 1.

Метод 2. Для нахождения точки пересечения прямых L₁ и L₂ решим совместно уравнения (12) и (13). Из уравнений (12) и (13) следует:

Из каждого уравнения (17),(18),(19) находим переменную t. Далее из полученных значений t выбираем те, которые удовлетворяют всем уравнениям (17)−(19). Если такое значение t не существует, то прямые не пересекаются. Если таких значений больше одного, то прямые совпадают. Если же такое значение t единственно, то подставляя это зачение t в (12) или в (13), получим координаты точки пересечения прямых (12) и (13).

3. Точка пересечения прямых в пространстве, заданных в разных видах.

Если уравнения прямых заданы в разных видах, то можно их привести к одному виду (к каноническому или к параметрическому) и найти точку пересечения прямых, описанных выше.

4. Примеры нахождения точки пересечения прямых в пространстве.

Пример 1. Найти точку пересечения прямых L₁ и L₂:

Представим уравнение (20) в виде двух уравнений:

Сделаем перекрестное умножение в уравнениях (22) и (23):

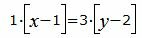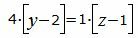Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:

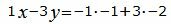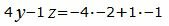Аналогичным образом поступим и с уравнением (2).

Представим уравнение (2) в виде двух уравнений:

Сделаем перекрестное умножение в уравнениях (7) и (8)

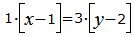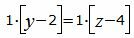Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:

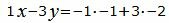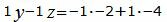Решим систему линейных уравнений (24), (25), (28), (29) с тремя неизвестными x, y, z. Для этого представим эту систему в виде матричного уравнения:

Решим систему линейных уравнений (30) отностительно x, y, z. Для решения системы, построим расширенную матрицу:

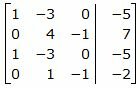Обозначим через a_ij элементы i-ой строки и j-ого столбца.

Первый этап. Прямой ход Гаусса.

Исключим элементы 1-го столбца матрицы ниже элемента a_{1 1}. Для этого сложим строку 3 со строкой 1, умноженной на −1:

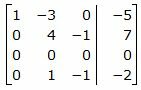Исключим элементы 2-го столбца матрицы ниже элемента a₂₂. Для этого сложим строку 4 со строкой 2, умноженной на −1/4:

Сделаем перестановку строк 3 и 4.

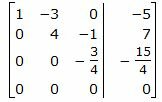Второй этап. Обратный ход Гаусса.

Исключим элементы 3-го столбца матрицы выше элемента a₃₃. Для этого сложим строку 2 со строкой 3, умноженной на −4/3:

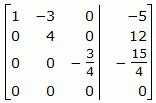Исключим элементы 2-го столбца матрицы выше элемента a₂₂. Для этого сложим строку 1 со строкой 2, умноженной на 3/4:

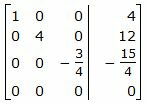Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):

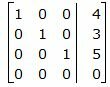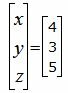Ответ. Точка пересечения прямых L₁ и L₂ имеет следующие координаты:

Пример 2. Найти точку пересечения прямых L₁ и L₂:

Приведем параметрическое уравнение прямой L₁ к каноническому виду. Выразим параметр t через остальные переменные:

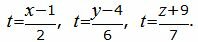Из равентсв выше получим каноническое уравнение прямой:

Представим уравнение (33) в виде двух уравнений:

Сделаем перекрестное умножение в уравнениях (34 и (35):

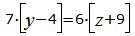Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:

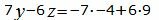Аналогичным образом поступим и с уравнением (2).

Представим уравнение (2) в виде двух уравнений:

Сделаем перекрестное умножение в уравнениях (38) и (39)

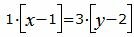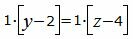Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:

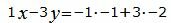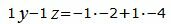Решим систему линейных уравнений (36), (37), (40), (41) с тремя неизвестными x, y, z. Для этого представим эту систему в виде матричного уравнения:

Решим систему линейных уравнений (42) отностительно x, y, z. Для решения системы, построим расширенную матрицу:

Обозначим через a_ij элементы i-ой строки и j-ого столбца.

Первый этап. Прямой ход Гаусса.

Исключим элементы 1-го столбца матрицы ниже элемента a_{1 1}. Для этого сложим строку 3 со строкой 1, умноженной на −1/6:

Исключим элементы 2-го столбца матрицы ниже элемента a₂₂. Для этого сложим строки 3 и 4 со строкой 2, умноженной на 8/21 и −1/7, соответственно:

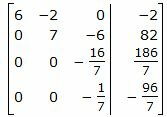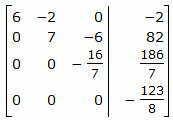Из расширенной матрицы восстановим последнюю систему линейных уравнений:

Уравнение (43) несовместна, так как несуществуют числа x, y, z удовлетворяющие уравнению (43). Следовательно система линейных уравнений (42) не имеет решения. Тогда прямые L₁ и L₂ не пересекаются. То есть они или параллельны, или скрещиваются.

Источник