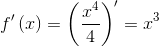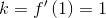Как находить угловой коэффициент касательной

Уравнение касательной к графику функции

п.1. Уравнение касательной

п.2. Алгоритм построения касательной

На входе: уравнение кривой \(y=f(x)\), абсцисса точки касания \(x_0\).
Шаг 1. Найти значение функции в точке касания \(f(x_0)\)
Шаг 2. Найти общее уравнение производной \(f’ (x)\)
Шаг 3. Найти значение производной в точке касания \(f'(x_0 )\)
Шаг 4. Записать уравнение касательной \(y=f’ (x_0)(x-x_0)+f(x_0)\), привести его к виду \(y=kx+b\)
На выходе: уравнение касательной в виде \(y=kx+b\)

Пусть \(f(x)=x^2+3\). Найдем касательную к этой параболе в точке \(x_0=1\).

п.3. Вертикальная касательная

Не путайте вертикальные касательные с вертикальными асимптотами.
Вертикальная асимптота проходит через точку разрыва 2-го рода \(x_0\notin D\), в которой функция не определена и производная не существует. График функции приближается к асимптоте на бесконечности, но у них никогда не бывает общих точек.
А вертикальная касательная проходит через точку \(x_0\in D\), входящую в область определения. График функции и касательная имеют одну общую точку \((x_0,y_0)\).

Вертикальные касательные характерны для радикалов вида \(y=\sqrt[n]\).

Пусть \(f(x)=\sqrt[5]+1\). Найдем касательную к этой кривой в точке \(x_0=1\).

\(f(x_0)=\sqrt[5]<1-1>+1=1\)
\(f'(x)=\frac15(x-1)^<\frac15-1>+0=\frac15(x-1)^<-\frac45>=\frac<1><5(x-1)^<\frac45>> \)
\(f'(x_0)=\frac<1><5(1-1)^<\frac45>>=\frac10=+\infty\)
В точке \(x_0\) проходит вертикальная касательная.
Её уравнение: \(x=1\)
Ответ: \(y=2x+2\)

п.4. Примеры

Пример 1. Для функции \(f(x)=2x^2+4x\)
a) напишите уравнения касательных, проведенных к графику функции в точках его пересечения с осью OX.

б) Найдите, в какой точке касательная образует с положительным направлением оси OX угол 45°. Напишите уравнение этой касательной.

в) найдите, в какой точке касательная будет параллельна прямой \(2x+y-6=0\). Напишите уравнение этой касательной.

Найдем угловой коэффициент заданной прямой: \(y=-2x+6\Rightarrow k=-2\). Касательная должна быть параллельной, значит, её угловой коэффициент тоже \(k=-2\). Получаем уравнение: \begin f'(x_0)=-2\\ 4x_0+4=-2\Rightarrow 4x_0=-6\Rightarrow x_0=-\frac32 \end Точка касания \(x_0=-\frac32\) \begin f(x_0)=2\cdot\left(-\frac32\right)^2+4\cdot\left(-\frac32\right)=\\ =\frac92-6=-\frac32 \end Уравнение касательной: \begin y=-2\cdot\left(x+\frac32\right)-\frac32=-2x-\frac92 \end Или, в каноническом виде: \begin 2x+y+\frac92=0 \end

г) в какой точке функции можно провести горизонтальную касательную? Напишите уравнение этой касательной.

У горизонтальной прямой \(k=0\). Получаем уравнение: \(f'(x_0)=0\). \begin 4x_0+4=0\Rightarrow 4x_0=-4\Rightarrow x_0=-1 \end Точка касания \(x_0=-1\) \begin f(x_0)=2\cdot(-1)^2+4\cdot(-1)=-2 \end Уравнение касательной: \begin y=0\cdot(x+1)-2=-2 \end

Ответ: а) \(y=4x\) и \(y=-4x-8\); б) \(y=x-\frac98\); в) \(2x+y+\frac92=0\); г) \(y=-2\)

Пример 3*. Найдите точку, в которой касательная к графику функции \(f(x)=\frac-x\) перпендикулярна прямой \(y=11x+3\). Напишите уравнение этой касательной.

Угловой коэффициент данной прямой \(k_1=11\).
Угловой коэффициент перпендикулярной прямой \(k_2=-\frac<1>=-\frac<1><11>\) \begin f'(x)=\left(\frac\right)’-x’=\frac<2x(x+3)-(x^2+2)\cdot 1><(x+3)^2>-1=\frac<2x^2+6x-x^2-2-(x+3)^2><(x+3)^2>=\\ =\frac<(x+3)^2>=- \frac<11> <(x+3)^2>\end В точке касания: \begin f'(x_0)=k_2\Rightarrow=-\frac<11><(x+3)^2>=-\frac<1><11>\Rightarrow (x+3)^2=121\Rightarrow (x+3)^2-11^2=0\Rightarrow\\ \Rightarrow (x+14)(x+8)=0\Rightarrow \left[ \begin x=-14\\ x=8 \end \right. \end
Уравнение касательной при \(x_0=-14\) \begin f(x_0)=\frac<(-14)^2+2><-14+3>+14=\frac<198><-11>+14=-18+14=-4\\ y=-\frac<1><11>(x+14)-4=-\frac <11>\end Уравнение касательной при \(x_0=8\) \begin f(x_0)=\frac<8^2+2><8+3>-8=\frac<66><11>-8=-2\\ y=-\frac<1><11>(x-8)-2=-\frac <11>\end
Ответ: точка касания (-14;-4), уравнение \(y=-\frac<11>\)
и точка касания (8;-2), уравнение \(-\frac<11>\)

Пример 4*. Найдите уравнения общих касательных к параболам \(y=x^2-5x+6\) и \(y=x^2+x+1\). Укажите точки касания.

Пример 5*. Докажите, что кривая \(y=x^4+3x^2+2x\) не пересекается с прямой \(y=2x-1\), и найдите расстояние между их ближайшими точками.

Чтобы найти расстояние, необходимо построить касательную к кривой с тем же угловым коэффициентом \(k=2\), то и y данной прямой. Тогда искомым расстоянием будет расстояние от точки касания до прямой \(y=2x-1\).
Строим уравнение касательной. По условию: \(f'(x)=4x^3+6x+2=2\) \begin 4x^3+6x=0\Rightarrow 2x(2x^2+3)=0\Rightarrow \left[ \begin x=0\\ 2x^2+3=0 \end \right. \Rightarrow \left[ \begin x=0\\ x^2=-\frac32 \end \right. \Rightarrow \left[ \begin x=0\\ x\in\varnothing \end \right. \Rightarrow x=0 \end Точка касания \(x_0=0,\ y_0=0^4+3\cdot 0^2+2\cdot 0=0\).
Уравнение касательной: \(y=2(x-0)+0=2x\)

Ищем расстояние между двумя параллельными прямыми: \(y=2x\) и \(y=2x-1\). Перпендикуляр из точки (0;0) на прямую \(y=2x-1\) имеет угловой коэффициент \(k=-\frac12\), его уравнение: \(y=-\frac12 x+b\). Т.к. точка (0;0) принадлежит этому перпендикуляру, он проходит через начало координат и \(b=0\).

Уравнение перпендикуляра: \(y=-\frac x2\).
Находим точку пересечения прямой \(y=2x-1\) и перпендикуляра \(y=-\frac x2\): \begin 2x-1=-\frac x2\Rightarrow 2,5x=1\Rightarrow x=0,4;\ y=-\frac<0,4><2>=-0,2 \end Точка пересечения A(0,4;-0,2).
Находим расстояние \(OA=\sqrt<0,4^2+(-0,2)^2>=0,2\sqrt<2^2+1^2>=\frac<\sqrt<5>><5>\)
Ответ: \(\frac<\sqrt<5>><5>\)

Источник

Уравнение касательной к графику функции (ЕГЭ 2022)

Чтобы разобраться с этой темой, нужно знать что такое производная.

Сейчас проверим, знаешь ли ты ее… 🙂

Найди приращение функции \( y=<^<2>>+2x+3\) при приращении аргумента, равном \( \Delta x\).

Должно получиться \( \Delta y=\Delta x\left( \Delta x+2x+2 \right)\).

А теперь найди производную функции \( y\left( x \right)=3<<\sin >^<2>>\sqrt\) в точке \( <_<0>>=\frac<<\pi >^<2>><16>\).

Если в каком-нибудь из этих примеров возникли сложности, настоятельно рекомендую вернуться к теме «Производная» и проштудировать ее еще раз.

Знаю, тема очень большая, но иначе нет смысла идти дальше…

А если ты справился, то в путь!

Уравнение касательной к графику функции — коротко о главном

Геометрический смысл производной

Производная функции в конкретной точке равна тангенсу угла наклона касательной к графику функции в этой точке, или угловому коэффициенту этой касательной:

Уравнение касательной

Уравнение касательной к графику функции \( f\left( x \right)\) в точке \( <_<0>>\):

Алгоритм действий для нахождения уравнения касательной

Геометрический смысл производной

Если плохо разбираешься в производной, то вот тебе полноценный гид по ней, с текстом, примерами и вебинарами: «Производная функции – геометрический смысл и правила дифференцирования»!

Рассмотрим график какой-то функции \( y=f\left( x \right)\):

Выберем на линии графика некую точку \( A\). Пусть ее абсцисса \( <_<0>>\), тогда ордината равна \( f\left( <_<0>> \right)\).

Затем выберем близкую к точке \( A\) точку \( B\) с абсциссой \( <_<0>>+\Delta x\); ее ордината – это \( f\left( <_<0>>+\Delta x \right)\):

Проведем прямую через эти точки. Она называется секущей (прямо как в геометрии).

Обозначим угол наклона прямой к оси \( Ox\) как \( \alpha \).

Как и в тригонометрии, этот угол отсчитывается от положительного направления оси абсцисс против часовой стрелки.

Какие значения может принимать угол \( \alpha \)?

Как ни наклоняй эту прямую, все равно одна половина будет торчать вверх. Поэтому максимально возможный угол – \( 180<>^\circ \), а минимально возможный – \( 0<>^\circ \).

Значит, \( \alpha \in \left[ 0<>^\circ ;180<>^\circ \right)\). Угол \( 180<>^\circ \) не включается, поскольку положение прямой в этом случае в точности совпадает с \( 0<>^\circ \), а логичнее выбирать меньший угол.

Возьмем на рисунке такую точку \( C\), чтобы прямая \( AC\) была параллельна оси абсцисс, а \( BC\) – ординат:

По рисунку видно, что \( AC=\Delta x\), а \( BC=\Delta f\).

Тогда отношение приращений:

(так как \( \angle C=90<>^\circ \), то \( \triangle ABC\) – прямоугольный).

Давай теперь уменьшать \( \Delta x\).

Тогда точка \( B\) будет приближаться к точке \( A\). Когда \( \Delta x\) станет бесконечно малым \( \left( \Delta x\to 0 \right)\), отношение \( \frac<\Delta f><\Delta x>\) станет равно производной функции в точке \( <_<0>>\).

Что же при этом станет с секущей?

Точка \( B\) будет бесконечно близка к точке \( A\), так что их можно будет считать одной и той же точкой.

Но прямая, имеющая с кривой только одну общую точку – это ни что иное, как касательная (в данном случае это условие выполняется только на небольшом участке – вблизи точки \( A\), но этого достаточно).

Говорят, что при этом секущая занимает предельное положение.

Угол наклона секущей к оси \( \displaystyle Ox\) назовем \( \varphi \). Тогда получится, что производная

Производная равна тангенсу угла наклона касательной к графику функции в данной точке

Поскольку касательная – это прямая, давай теперь вспомним уравнение прямой:

За что отвечает коэффициент \( \displaystyle k\)? За наклон прямой. Он так и называется: угловой коэффициент.

Что это значит? А то, что равен он тангенсу угла между прямой и осью \( \displaystyle Ox\)!

То есть вот что получается:

Но мы получили это правило, рассматривая возрастающую функцию. А что изменится, если функция будет убывающей?

Посмотрим: Теперь углы \( \alpha \) и \( \displaystyle \varphi \) тупые. А приращение функции \( \Delta f\) – отрицательное.

Получаем: \( \frac<-\Delta f><\Delta x>=-\ \alpha \text< >\Rightarrow \text< >\frac<\Delta f><\Delta x>=\ \alpha \), то есть все, как и в прошлый раз.

Снова устремим точку \( \displaystyle B\) к точке \( \displaystyle A\), и секущая \( \displaystyle AB\) примет предельное положение, то есть превратится в касательную к графику функции в точке \( \displaystyle A\).

Итак, сформулируем окончательно полученное правило:

Производная функции в данной точке равна тангенсу угла наклона касательной к графику функции в этой точке, или (что то же самое) угловому коэффициенту этой касательной:

Это и есть геометрический смысл производной.

Окей, все это интересно, но зачем оно нам? Вот пример:

На рисунке изображен график функции \( \displaystyle y=\mathsf\left( x \right)\) и касательная к нему в точке с абсциссой \( <_<0>>\).

Найдите значение производной функции \( \displaystyle \mathsf\left( x \right)\) в точке \( <_<0>>\).

Решение.

Как мы недавно выяснили, значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс:

\( \displaystyle f’\left( x \right)=k=\ \varphi\).

Значит, для нахождения значения производной нам нужно найти тангенс угла наклона касательной.

На рисунке у нас отмечено две точки, лежащие на касательной, координаты которых нам известны. Так давай достроим прямоугольный треугольник, проходящий через эти точки, и найдем тангенс угла наклона касательной!

Угол наклона касательной к оси \( \displaystyle Ox\) – это \( \displaystyle \angle BAC\). Найдем тангенс этого угла:

Таким образом, производная функции \( \displaystyle \mathsf\left( x \right)\) в точке \( <_<0>>\) равна \( \displaystyle 1,2\).

Ответ: \( \displaystyle 1,2\).

Теперь попробуй сам.

Еще статью на геометрический смысл производной ты найдешь здесь: «Геометрический смысл производной«.

Решим два примера

Пример 1. На рисунке изображен график функции \( \displaystyle y=\mathsf\left( x \right)\) и касательная к нему в точке с абсциссой \( <_<0>>\). Найдите значение производной функции \( \displaystyle \mathsf\left( x \right)\) в точке \( <_<0>>\);

Пример 2. На рисунке изображен график функции \( \displaystyle y=\mathsf\left( x \right)\) и касательная к нему в точке с абсциссой \( <_<0>>\). Найдите значение производной функции \( \displaystyle \mathsf\left( x \right)\) в точке \( <_<0>>\).

Решение примера №1

Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс:

\( \displaystyle k=f’\left( x \right)=\ \beta\).

Достроим треугольник со стороной \( \displaystyle AC\), лежащей на касательной.

Угол наклона касательной – это угол, отмеченный зеленым на графике.

Он тупой \( \left( >90<>^\circ \right)\), поэтому его тангенс не получится вычислить так же, как в предыдущем примере (ведь в прямоугольном треугольнике не может быть тупого угла).

Применим знания из тригонометрии:

Источник

Нахождение углового коэффициента касательной.

Если имеется кривая заданная функцией y=f(x), то угловой коэффициент касательной в точке с абсциссой x₀ находят по формуле

Например 1. Найти угловой коэффициент касательной, проведенной к графику функции

в точке с абсциссой х₀=1.
Решение. Находим производную функции

Тогда при x₀=1 значение производной равно

Отсюда получаем, что угловой коэффициент касательной в точке с абсциссой х₀=1 равен

Нахождение угла наклона касательной к графику функции.

Геометрический смысл производной заключается в том, что производная равна угловому коэффициенту касательной и тангенсу угла наклона.

Как найти угол наклона касательной к графику функции y=f(x) в точке x_0.

Например. Найти наклона касательной, проведенной к графику функции

в точке с абсциссой х₀=1.
Решение. Находим производную функции

Тогда при x₀=1 значение производной равно ,где

. Отсюда находим угол .

Исследование функции с помощью производной.

Если производная дифференцируемой функции положительна внутри некоторого промежутка Х, то она возрастает на этом промежутке.

Если производная дифференцируемой функции отрицательна внутри некоторого промежутка Х, то она убывает на этом промежутке.

Промежутки возрастания и убывания функции называются интервалами монотонностиданной функции.

Экстремумы функции.

Точка X0 называется точкой максимума функции f (x), если существует такая окрестность точки X0, что для всех X из этой окрестности выполняется неравенство f (x) f (x0).

Теорема Ферма.
(Необходимое условие экстремума)
Если X0 – точка экстремума функции f (x), то f’ (x0)=0

Точки в которых f’ (x)=0 называются стационарными или критическими.

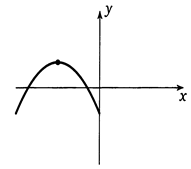
Точки, в которых производная функции равна нулю на графике функции выглядят так:

Достаточное условие существования экстремума (максимума) в точке.

Если при переходе через стационарную точку производная функции меняет знак с “+” на “-”, то эта точка является точкой максимума.

Если при переходе через стационарную точку f’ (x) не меняет знак, то эта точка не является точкой экстремума, такие точки называются точками перегиба.

Алгоритм нахождения экстремумов функции.

1. Найти производную функции.

2. Найти стационарные точки (решить уравнение f’ (x)=0).

3.На числовой прямой определить знак производной на полученных интервалах.

4.Определить точки экстремумов функции (использовать определение).

5. Записать ответ.

Например: Найти экстремумы функции

1.

2.

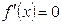
3.___+____.___-____.___+_______

4.Х=0 – точка максимума, т. К. при переходе через стационарную точку производная сменила знак с «+» на «-»;

Х=2 – точка минимума, т. К. при переходе через стационарную точку производная сменила знак с «-» на «+»;

5. ответ: х=0 – точка максимума, х=2 – точка минимума.

Источник

Алгебра и начала математического анализа. 11 класс

Конспект урока

Алгебра и начала анализа, 11 класса.

Урок №14. Геометрический смысл производной.

Перечень вопросов, рассматриваемых в теме

1) Геометрический смысл производной;

2) Алгоритм нахождения касательной к графику функции в точке;

3) Сравнение производных заданной функции по ее графику в различных точках.

Число k= tgα называется угловым коэффициентом прямой, а угол α – углом между этой прямой и осью Ох.

Геометрический смысл производной. Производная в точке x₀ равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл.– М.: Просвещение, 2014.

Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2017.

Теоретический материал для самостоятельного изучения

Напомним, что графиком линейной функции у=кх + b является прямая.

Число k= tgα называется угловым коэффициентом прямой, а угол α – углом между этой прямой и осью Ох.

Уравнение касательной: y=1-1(x-0) = 1-x

Найдем угловой коэффициент прямой 4х+у+4=0:

Касательная к параболе и данная прямая по условию параллельны. Следовательно, их угловые коэффициенты равны, т.е.

х=-1 – абсцисса точки касания.

Источник