Как находить углы между векторами
Угол между векторами.
 |
Формула вычисления угла между векторами
Примеры задач на вычисление угла между векторами
Примеры вычисления угла между векторами для плоских задачи
Решение: Найдем скалярное произведение векторов:
a · b = 3 · 4 + 4 · 3 = 12 + 12 = 24.
Найдем модули векторов:
| a | = √ 3 2 + 4 2 = √ 9 + 16 = √ 25 = 5
| b | = √ 4 2 + 3 2 = √ 16 + 9 = √ 25 = 5
Найдем угол между векторами:
| cos α = | a · b | = | 24 | = | 24 | = 0.96 |
| | a | · | b | | 5 · 5 | 25 |
Решение: Найдем скалярное произведение векторов:
a · b = 5 · 7 + 1 · 5 = 35 + 5 = 40.
Найдем модули векторов:
| a | = √ 7 2 + 1 2 = √ 49 + 1 = √ 50 = 5√ 2
| b | = √ 5 2 + 5 2 = √ 25 + 25 = √ 50 = 5√ 2
Найдем угол между векторами:
| cos α = | a · b | = | 40 | = | 40 | = | 4 | = 0.8 |
| | a | · | b | | 5√ 2 · 5√ 2 | 50 | 5 |
Примеры вычисления угла между векторами для пространственных задач
Решение: Найдем скалярное произведение векторов:
a · b = 3 · 4 + 4 · 4 + 0 · 2 = 12 + 16 + 0 = 28.
Найдем модули векторов:
| a | = √ 3 2 + 4 2 + 0 2 = √ 9 + 16 = √ 25 = 5
| b | = √ 4 2 + 4 2 + 2 2 = √ 16 + 16 + 4 = √ 36 = 6
Найдем угол между векторами:
| cos α = | a · b | = | 28 | = | 14 |
| | a | · | b | | 5 · 6 | 15 |
Решение: Найдем скалярное произведение векторов:
a · b = 1 · 5 + 0 · 5 + 3 · 0 = 5.
Найдем модули векторов:
| a | = √ 1 2 + 0 2 + 3 2 = √ 1 + 9 = √ 10
| b | = √ 5 2 + 5 2 + 0 2 = √ 25 + 25 = √ 50 = 5√ 2
Найдем угол между векторами:
cos α = a · b | a | · | b | = 5 √ 10 · 5√ 2 = 1 2√ 5 = √ 5 10 = 0.1√ 5
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Как найти угол между векторами
Угол между векторами
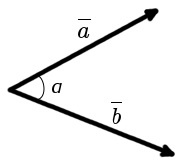
Угол между векторами — это угол между отрезками, которые изображают эти две направляющие и которые отложены от одной точки пространства. Другими словами — это кратчайший путь, на который можно повернуть один из векторов вокруг его начала до положения общей направленности со вторым.
На изображении это α, который также можно обозначить следующим образом:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Как и любой другой угол, векторный может быть представлен в нескольких вариациях.
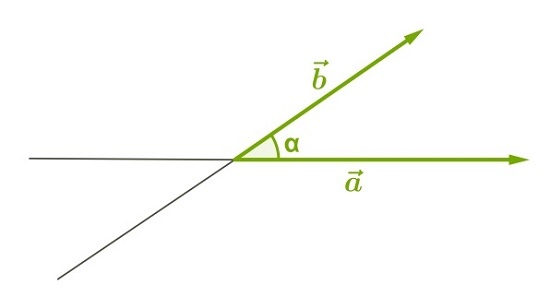
Острый:
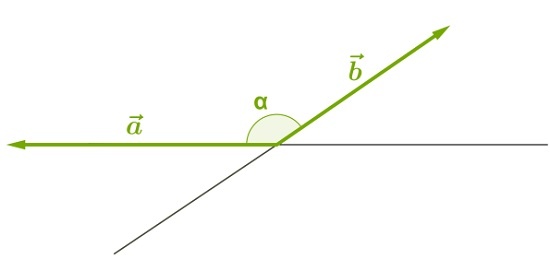
Тупой:
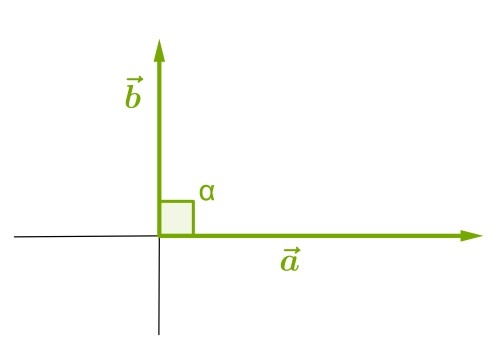
Прямой:
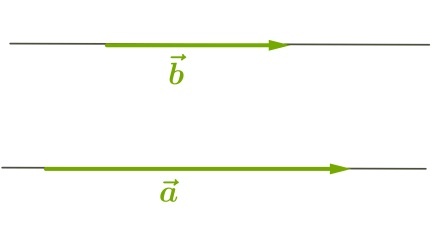
С величиной \(0^\circ\) (то есть, векторы сонаправлены):
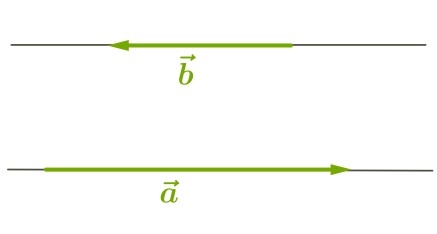
С величиной \(180^\circ\) (векторы направлены в противоположные стороны):
Нахождение угла между векторами
Как правило, угол между \( \overrightarrow a\) и \(\overrightarrow b\) можно найти с помощью скалярного произведения или теоремы косинусов для треугольника, который был построен на основе двух этих направляющих.
Скалярное произведение — это число, которое равно произведению двух направляющих на косинус угла между ними.
Формула скалярного произведения:
\(\left(\overrightarrow a;\overrightarrow b\right)=\left|\overrightarrow a\right|\times\left|\overrightarrow b\right|\times\cos\left(\widehat<\overrightarrow a;\overrightarrow b>\right)\)
В случае, если \overrightarrow a и \overrightarrow b не нулевые, можно найти косинус α между ними, опираясь на формулу:
Расчет угла, если вектор задан координатами
Если же координаты находятся в трехмерном пространстве и заданы в виде:
то формула принимает такой вид:
Расчет угла, если заданы три точки в прямоугольной системе координат
В этом случае проще будет разобраться с объяснениями сразу на примере.
Решение
Для начала найдем их координаты по известным координатам заданных точек:
После этого уже можем применить формулу для определения косинуса угла на плоскости и подставить известные значения:
Примеры решения задач
Для наглядности, взглянем на примеры решения задач по данной теме.
Задача 1
Решение
Подставим известные значения:
Далее найдем угол между данными векторами:
Задача 2
Решение
Используем формулу для нахождения косинуса угла между направляющими в трехмерной системе координат:
Подставляем значения и получаем:
Теперь находим угол α:
Задача 3
Онлайн калькулятор. Вычисление угла между векторами
Этот онлайн калькулятор позволит вам очень просто найти угол между двумя векторами (косинус угла между векторами) для плоских и пространственных задач.
Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление угла между векторами и закрепить пройденный материал.
Калькулятор для вычисления угла между векторами
Инструкция использования калькулятора для вычисления угла между векторами
Ввод даных в калькулятор для вычисления угла между векторами
В онлайн калькулятор можно вводить числа или дроби. Более подробно читайте в правилах ввода чисел.
Дополнительные возможности калькулятора для вычисления угла между векторами
Теория. Вычисление угла между векторами
Угол между двумя векторами a и b можно найти использовав следующую формулу:
| cos α = | a · b |
| | a || b | |
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Нахождение угла между векторами
Длина вектора, угол между векторами – эти понятия являются естественно-применимыми и интуитивно понятными при определении вектора как отрезка определенного направления. Ниже научимся определять угол между векторами в трехмерном пространстве, его косинус и рассмотрим теорию на примерах.
Очевидно, что угол имеет возможность принимать значения от 0 до π или от 0 до 180 градусов.
Векторы называются перпендикулярными, если угол между ними равен 90 градусов или π 2 радиан.
Нахождение угла между векторами
Косинус угла между двумя векторами, а значит и собственно угол, обычно может быть определен или при помощи скалярного произведения векторов, или посредством теоремы косинусов для треугольника, построенного на основе двух данных векторов.
Если заданные векторы a → и b → ненулевые, то можем разделить правую и левую части равенства на произведение длин этих векторов, получая, таким образом, формулу для нахождения косинуса угла между ненулевыми векторами:
Данная формула используется, когда в числе исходных данных есть длины векторов и их скалярное произведение.
Решение
Чаще встречаются задачи, где векторы задаются координатами в прямоугольной системе координат. Для таких случаев необходимо вывести ту же формулу, но в координатной форме.
Решение
Также распространены задачи, когда заданы координаты трех точек в прямоугольной системе координат и необходимо определить какой-нибудь угол. И тогда, для того, чтобы определить угол между векторами с заданными координатами точек, необходимо вычислить координаты векторов в виде разности соответствующих точек начала и конца вектора.
Решение
и отсюда выведем формулу косинуса угла:
Для применения полученной формулы нам нужны длины векторов, которые несложно определяются по их координатам.
Хотя указанный способ имеет место быть, все же чаще применяют формулу:
Как найти угол между векторами
Вы будете перенаправлены на Автор24
Угол между векторами
Для того, чтобы мы могли ввести формулу для вычисления угла между векторами через координаты, нужно сначала разобраться с самим понятием угла между этими векторами.
Рисунок 1. Угол между векторами. Автор24 — интернет-биржа студенческих работ
Нахождение угла между векторами в пространстве с помощью скалярного произведения
Вспомним сначала, что называется скалярным произведением и каким образом его можно находить.
Скалярным произведением двух векторов будем называть такой скаляр (или число), который равняется произведению длин двух этих векторов с косинусом угла между данными векторами.
Математически это может выглядеть следующим образом:
Также, помимо того, как из самого определения 1, для нахождения скалярного произведения можно пользоваться следующей теоремой.
Математически выглядит следующим образом
$\overline<δ>\cdot \overline<β>=δ_1 δ_2+β_1 β_2+γ_1 γ_2$
Готовые работы на аналогичную тему
Найдя значение косинуса, мы легко найдем и значение самого угла.
Решение.
Найдем скалярное произведение между данными векторами через координаты:
$\overline<δ>\cdot \overline<β>=1\cdot 3+(-2)\cdot 0+2\cdot 4=11$
Найдем длины этих векторов:
В результате, получим
Нахождение угла между векторами с помощью векторного произведения
Вспомним сначала, определение векторного произведения и каким образом его можно находить.
Векторным произведением двух векторов называется такой вектор, который будет перпендикулярен обоим данным векторам, и его длина равна произведению длин этих векторов с синусом угла между данными векторами, а также этот вектор с двумя начальными имеют ту же ориентацию, как и декартова система координат.
Математически это выглядит следующим образом:
Рисунок 2. Векторное произведение. Автор24 — интернет-биржа студенческих работ
Для нахождения вектора векторного произведения можно пользоваться следующей формулой:
Найдем вектор векторного произведения по формуле:
$\overline<δ>х\overline<β>=\begin
Найдя значение синуса, мы легко найдем и значение самого угла между векторами через координаты через формулу.
Решение.
Найдем вектор векторного произведения между данными векторами по формуле:
Найдем длины этих векторов:
В результате, получим
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 20 07 2021