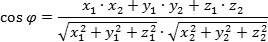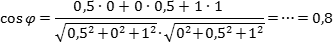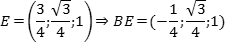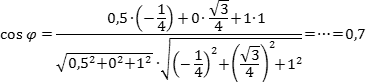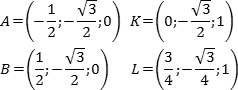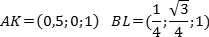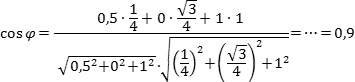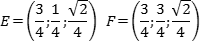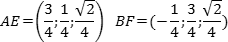Как находить угол между прямыми

Угол между прямыми

Определение угла между прямыми

Угол между прямыми на плоскости

Угол между прямыми заданными уравнениями с угловым коэффициентом

то угол между ними можно найти, используя формулу:

Если знаменатель равен нулю (1 + k ₁· k ₂ = 0), то прямые перпендикулярны.

Соответственно легко найти угол между прямыми

Угол между прямыми через направляющие векторы этих прямых

cos φ = | a · b | | a | · | b |

Если уравнение прямой задано параметрически

x = l t + a y = m t + b

то вектор направляющей имеет вид

Если уравнение прямой задано как

Если дано каноническое уравнение прямой

то вектор направляющей имеет вид

Если задано уравнение прямой с угловым коэффициентом

то для вычисления направляющего вектора, можно взять две точки на прямой, например, при x = 0 => y = b значит точка на прямой имеет координаты K(0, b ), при x = 1 => y = k + b значит точка на прямой имеет координаты M(1, k + b ). Вектор направляющей KM =

Угол между прямыми через векторы нормалей этих прямых

cos φ = | a · b | | a | · | b |

Если уравнение прямой задано как

то вектор нормали имеет вид

Если задано уравнение прямой с угловым коэффициентом

то вектор нормали имеет вид

Угол между прямыми через направляющий вектор и вектор нормали этих прямых

sin φ = | a · b | | a | · | b |

Примеры задач на вычисления угла между прямыми на плоскости

Решение: Воспользуемся формулой для вычисления угла между прямыми заданными уравнениями с угловым коэффициентом:

Решение: Воспользуемся формулой для вычисления угла между прямыми у которых известны направляющие векторы.

Для первой прямой направляющий вектор <1; 2>, для второй прямой направляющий вектор

cos φ = |1 · 2 + 2 · 1| 1 2 + 2 2 · 2 2 + 1 2 = 4 5 · 5 = 0.8

Решение: Для решения этой задачи можно найти направляющие векторы и вычислить угол через направляющие векторы или преобразовать уравнения в уравнения с угловым коэффициентом и вычислить угол через угловые коэффициенты.

Преобразуем имеющиеся уравнения в уравнения с угловым коэффициентом.

Угол между прямыми в пространстве

cos φ = | a · b | | a | · | b |

Если дано каноническое уравнение прямой

то направляющий вектор имеет вид

Если уравнение прямой задано параметрически

x = l t + a y = m t + b z = n t + c

то направляющий вектор имеет вид

cos φ = |2 · 1 + 1 · (-2) + (-1) · 0| 2 2 + 1 2 + (-1) 2 · 1 2 + (-2) 2 + 0 2 = 0 6 · 5 = 0

Решение: Для решения этой задачи найдем направляющие векторы этих прямых.

Уравнение первой прямой задано в канонической форме, поэтому направляющий вектор <3; 4; 5>.

Преобразуем второе уравнение к каноническому вид.

Получено уравнение второй прямой в канонической форме

Источник

Нахождение угла между прямыми

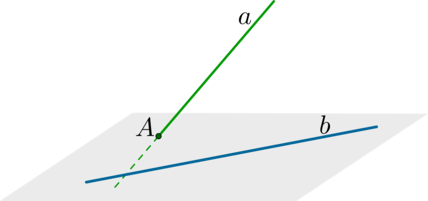
\(\blacktriangleright\) В пространстве существует 4 типа взаимного расположения прямых: совпадают, пересекаются, параллельны, скрещиваются.

\(\blacktriangleright\) Скрещивающиеся прямые – это прямые, через которые нельзя провести одну плоскость.

Признак скрещивающихся прямых: если первая прямая пересекает плоскость, в которой лежит вторая прямая, в точке, не лежащей на второй прямой, то такие прямые скрещиваются.

\(\blacktriangleright\) Порядок нахождения угла между скрещивающимися прямыми:

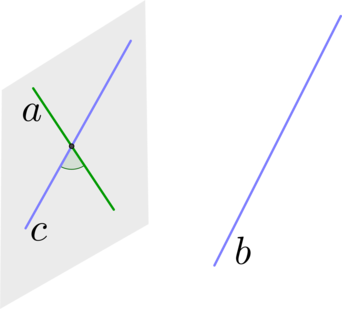
Шаг 1: через одну из двух прямых \(a\) провести плоскость, параллельную второй прямой \(b\) (напомним признак: прямая параллельна плоскости, если она параллельна какой-нибудь прямой из этой плоскости);

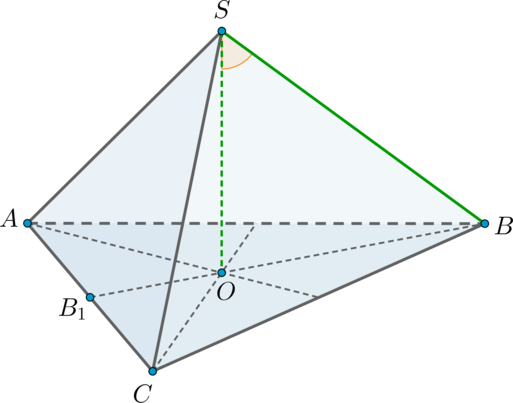
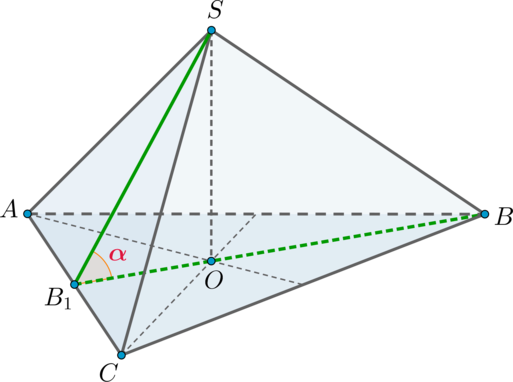
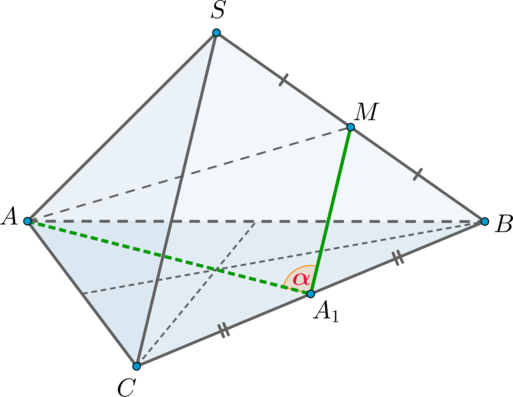
Так как пирамида правильная, то в основании лежит правильный треугольник, следовательно, высота \(SO\) падает в точку пересечения медиан основания.

Так как пирамида правильная, то в основании лежит правильный треугольник, следовательно, \(AA_1\) также является и медианой.

Каждому школьнику, который готовится к ЕГЭ по математике, будет полезно повторить тему «Нахождение угла между прямыми». Как показывает статистика, при сдаче аттестационного испытания задачи по данному разделу стереометрии вызывают трудности у большого количества учащихся. При этом задания, требующие найти угол между прямыми, встречаются в ЕГЭ как базового, так и профильного уровня. Это значит, что уметь их решать должны все.

Основные моменты

В пространстве существует 4 типа взаимного расположения прямых. Они могут совпадать, пересекаться, быть параллельными или скрещивающимися. Угол между ними может быть острым или прямым.

Для нахождения угла между прямыми в ЕГЭ или, например, в решении задач по теореме о трех перпендикулярах, школьники Москвы и других городов могут использовать несколько способов решения задач по данному разделу стереометрии. Выполнить задание можно путем классических построений. Для этого стоит выучить основные аксиомы и теоремы стереометрии. Школьнику нужно уметь логически выстраивать рассуждение и создавать чертежи, для того чтобы привести задание к планиметрической задаче.

Также можно использовать векторно-координатный метод, применяя простые формулы, правила и алгоритмы. Главное в этом случае — правильно выполнить все вычисления. Отточить свои навыки решения задач по стереометрии и другим разделам школьного курса вам поможет образовательный проект «Школково».

Источник

Угол между пересекающимися прямыми: определение, примеры нахождения

Данный материал посвящен такому понятию, как угол между двумя пересекающимися прямыми. В первом пункте мы поясним, что он из себя представляет, и покажем его на иллюстрациях. Потом разберем, какими способами можно найти синус, косинус этого угла и сам угол (отдельно рассмотрим случаи с плоскостью и трехмерным пространством), приведем нужные формулы и покажем на примерах, как именно они применяются на практике.

Что такое угол между пересекающимися прямыми

Для того чтобы понять, что такое угол, образующийся при пересечении двух прямых, нам потребуется вспомнить само определение угла, перпендикулярности и точки пересечения.

Мы называем две прямые пересекающимися, если у них есть одна общая точка. Эта точка называется точкой пересечения двух прямых.

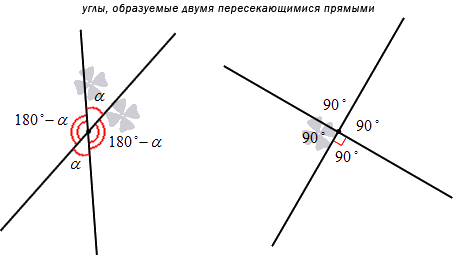
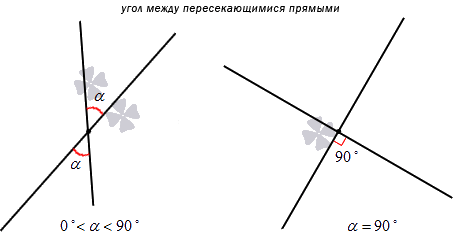
Каждая прямая разделяется точкой пересечения на лучи. Обе прямые при этом образуют 4 угла, из которых два – вертикальные, а два – смежные. Если мы знаем меру одного из них, то можем определить и другие оставшиеся.

Взгляните на рисунок:

Перейдем к формулированию основного определения.

Как найти угол между пересекающимися прямыми на плоскости

Умение находить меру угла между двумя пересекающимися прямыми полезно для решения многих практических задач. Метод решения можно выбрать из нескольких вариантов.

Для начала мы можем взять геометрические методы. Если нам известно что-то о дополнительных углах, то можно связать их с нужным нам углом, используя свойства равных или подобных фигур. Например, если мы знаем стороны треугольника и нужно вычислить угол между прямыми, на которых эти стороны расположены, то для решения нам подойдет теорема косинусов. Если у нас в условии есть прямоугольный треугольник, то для подсчетов нам также пригодится знание синуса, косинуса и тангенса угла.

Координатный метод тоже весьма удобен для решения задач такого типа. Поясним, как правильно его использовать.

Начнем с формулировки основного принципа нахождения угла в заданных условиях.

Нам известно, что с понятием прямой линии тесно связаны такие понятия, как направляющий и нормальный вектор. Если у нас есть уравнение некоторой прямой, из него можно взять координаты этих векторов. Мы можем сделать это сразу для двух пересекающихся прямых.

Угол, образуемый двумя пересекающимися прямыми, можно найти с помощью:

Теперь рассмотрим каждый способ отдельно.

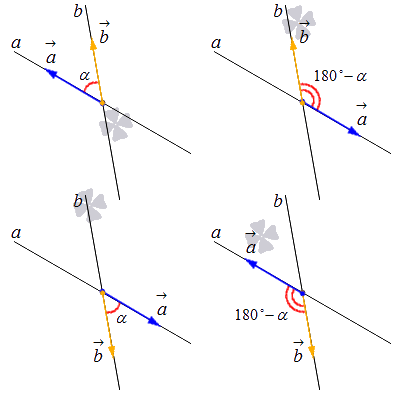
Во втором случае были использованы формулы приведения. Таким образом,

Запишем последнюю формулу словами:

Косинус угла, образованного двумя пересекающимися прямыми, будет равен модулю косинуса угла между его направляющими векторами.

Из нее мы можем вывести формулу косинуса угла между двумя заданными прямыми:

cos α = a x · b x + a y · b y a x 2 + a y 2 · b x 2 + b y 2 = a x · b x + a y · b y a x 2 + a y 2 · b x 2 + b y 2

Тогда сам угол можно найти по следующей формуле:

α = a r c cos a x · b x + a y + b y a x 2 + a y 2 · b x 2 + b y 2

Приведем пример решения задачи.

Решение

Ответ: данные прямые образуют угол в 45 градусов.

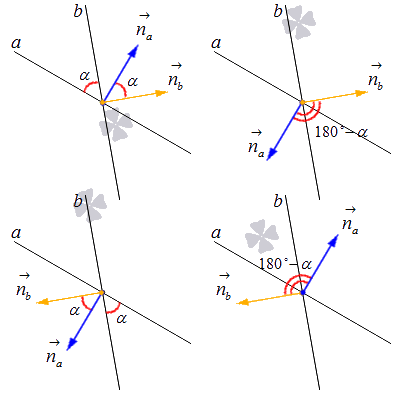
Формулы для вычисления косинуса угла между пересекающимися прямыми и самого этого угла с помощью координат нормальных векторов выглядят так:

Здесь n a → и n b → обозначают нормальные векторы двух заданных прямых.

Решение

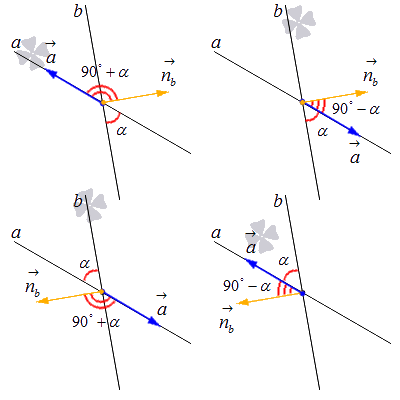
Разберем последний случай – нахождение угла между прямыми, если нам известны координаты направляющего вектора одной прямой и нормального вектора другой.

Если величина угла между заданными векторами не более 90 градусов, получается, что он будет дополнять угол между a и b до прямого угла.

Если он менее 90 градусов, то мы получим следующее:

Используя правило равенства косинусов равных углов, запишем:

Чтобы найти синус угла между двумя прямыми, пересекающимися на плоскости, нужно вычислить модуль косинуса угла между направляющим вектором первой прямой и нормальным вектором второй.

Запишем необходимые формулы. Нахождение синуса угла:

Нахождение самого угла:

α = a r c sin = a x · n b x + a y · n b y a x 2 + a y 2 · n b x 2 + n b y 2

Здесь a → является направляющим вектором первой прямой, а n b → – нормальным вектором второй.

Решение

Обратите внимание, что мы взяли уравнения из предыдущей задачи и получили точно такой же результат, но другим способом.

Ответ: α = a r c sin 7 2 34

Приведем еще один способ нахождения нужного угла с помощью угловых коэффициентов заданных прямых.

Решение

Ответ: α = a r c cos 23 2 34

В выводах этого пункта следует отметить, что приведенные здесь формулы нахождения угла не обязательно учить наизусть. Для этого достаточно знать координаты направляющих и/или нормальных векторов заданных прямых и уметь определять их по разным типам уравнений. А вот формулы для вычисления косинуса угла лучше запомнить или записать.

Как вычислить угол между пересекающимися прямыми в пространстве

Вычисление такого угла можно свести к вычислению координат направляющих векторов и определению величины угла, образованного этими векторами. Для таких примеров используются такие же рассуждения, которые мы приводили до этого.

Для нахождения самого угла нам понадобится эта формула:

α = a r c cos a x · b x + a y · b y + a z · b z a x 2 + a y 2 + a z 2 · b x 2 + b y 2 + b z 2

Решение

Источник

Угол между прямыми онлайн

С помощью этого онлайн калькулятора можно найти угол между прямыми. Дается подробное решение с пояснениями. Для вычисления угла между прямыми, задайте размерность (2-если рассматривается прямая на плоскости, 3- если рассматривается прямая в пространстве), выберите вид уравнения (канонический, параметрический, общий (для двухмерного пространства)), введите данные в ячейки и нажмите на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.

Предупреждение

1. Угол между прямыми на плоскости

Прямые заданы каноническими уравнениями

1.1. Определение угла между прямыми

Пусть в двухмерном пространстве прямые L₁ и L₂ заданы каноническими уравнениями

Задача об определении угла между прямыми L₁ и L₂ сводится к задаче об определении угла между направляющими векторами q₁ и q₂ (рис.1).

Из выражения (1.3) получим:

.

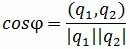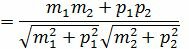(1.4)

Таким образом, из формулы (1.4) можно найти угол между прямыми L₁ и L₂. Как видно из Рис.1 пересекающиеся прямые образуют смежные углы φ и φ₁. Если найденный угол больше 90°, то можно найти минимальный угол между прямыми L₁ и L₂: φ₁=180-φ.

Из формулы (1.4) можно вывести условия параллельности и перпендикулярности двух прямых.

Пример 1. Определить угол между прямыми

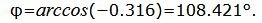Данный угол больше 90°. Найдем минимальный угол между прямыми. Для этого вычтем этот угол из 180:

Угол между прямыми равен:

1.2. Условие параллельности прямых

Пусть φ=0. Тогда cosφ=1. При этом выражение (1.4) примет следующий вид:

Сделаем преобразования с выражением (1.7):

,

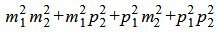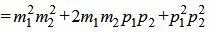Таким образом условие параллельности прямых L₁ и L₂ имеет вид (1.8). Если m₂≠0 и p₂≠0, то (1.8) можно записать так:

Пример 2. Определить, параллельны ли прямые

, .

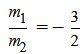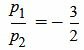Удовлетворяется равенство (1.9), следовательно прямые (1.10) и (1.11) параллельны.

Ответ. Прямые (1.10) и (1.11) параллельны.

1.3. Условие перпендикулярности прямых

Пусть φ=90°. Тогда cosφ=0. При этом выражение (1.4) примет следующий вид:

Пример 3. Определить, перпендикулярны ли прямые

Удовлетворяется условие (1.13), следовательно прямые (1.14) и (1.15) перпендикулярны.

Ответ. Прямые (1.14) и (1.15) перпендикулярны.

Прямые заданы общими уравнениями

1.4. Определение угла между прямыми

Пусть две прямые L₁ и L₂ заданы общими уравнениями

Так как нормальным вектором прямой L₁ является n₁=(A₁, B₁), а нормальным вектором прямой L₂ является n₂=(A₂, B₂), то задача об определении угла между прямыми L₁ и L₂ сводится к определению угла φ между векторами n₁ и n₂ (Рис.2).

Из определения скалярного произведения двух векторов, имеем:

Из уравнения (19) получим

.

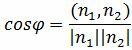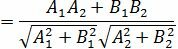(1.20)

Пример 4. Найти угол между прямыми

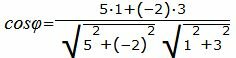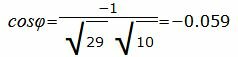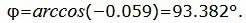Данный угол больше 90°. Найдем минимальный угол между прямыми. Для этого вычтем этот угол из 180:

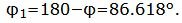1.5. Условие параллельности прямых

Так как угол между паралленьными прямыми равен нулю, то φ=0, cos(φ)=1. Тогда сделав преобразования, представленные выше для канонических уравнений прямых получим условие параллельности:

С другой стороны условие параллельности прямых L₁ и L₂ эквивалентно условию коллинеарности векторов n₁ и n₂ и можно представить так:

Как видим уравнения (1.24) и (1.25) эквивалентны при A₂≠0 и B₂≠0. Если в координатах нормальных векторов существует нулевой коэффициент, то нужно использовать уравнение (1.24).

Пример 5. Определить, параллельны ли прямые

Удовлетворяется равенство (1.24), следовательно прямые (1.26) и (1.27) параллельны.

Ответ. Прямые (1.26) и (1.27) параллельны.

1.6. Условие перпендикулярности прямых

Условие перпендикулярности прямых L₁ и L₂ можно извлекать из формулы (1.20), подставляя cos(φ)=0. Тогда скалярное произведение (n₁,n₂)=0. Откуда

Таким образом условие перпендикулярности прямых определяется равенством (1.28).

Пример 6. Определить, перпендикулярны ли прямые

Удовлетворяется равенство (1.28), следовательно прямые (1.29) и (1.30) перпендикулярны.

Ответ. Прямые (1.29) и (1.30) перпендикулярны.

2. Угол между прямыми в пространстве

2.1. Определение угла между прямыми

Пусть в пространстве прямые L₁ и L₂ заданы каноническими уравнениями

Из выражения (2.3) получим:

.

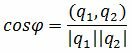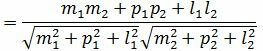(2.4)

Таким образом, из формулы (2.4) можно найти угол между прямыми L₁ и L₂. Если найденный угол больше 90°, то можно найти минимальный угол между прямыми L₁ и L₂: φ₁=180-φ.

Из формулы (2.4) можно вывести условия параллельности и перпендикулярности двух прямых.

Пример 1. Определить угол между прямыми

.

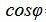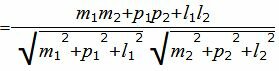Угол между прямыми равен:

2.2. Условие параллельности прямых

Условие параллельности прямых эквивалентно условию коллинеарности направляющих векторов q₁ и q₂, т.е. соответствующие координаты этих векторов пропорциональны. Пусть

где α − некоторое число. Тогда соответствующие координаты векторов q₁ и q₂ пропорциональны, и, следовательно прямые L₁ и L₂ параллельны.

Условие параллельности прямых можно представить и так:

Отметим, что любую пропорцию нужно понимать как равенство ad=bc.

Пример 2. Определить, параллельны ли прямые

, , .

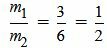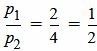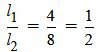Удовлетворяется равенство (2.8) (или (2.7)), следовательно прямые (2.9) и (2.10) параллельны.

Ответ. Прямые (2,9) и (2,10) параллельны.

Пример 3. Определить, параллельны ли прямые

Выражение (2.13) нужно понимать так:

, , .

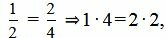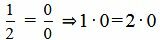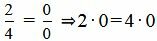(2.14)

Как мы видим из (2.14) условия (2.13) выполняются. Следовательно прямые (2.11) и (2.12) параллельны.

Ответ. Прямые (2.11) и (2.12) параллельны.

2.3. Условие перпендикулярности прямых

Пусть φ=90°. Тогда cosφ=0. При этом выражение (2.4) примет следующий вид:

Пример 3. Определить, перпендикулярны ли прямые

.

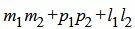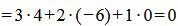(2.19)

Удовлетворяется условие (2.16), следовательно прямые (2.17) и (2.18) перпендикулярны.

Ответ. Прямые (2.17) и (2.18) перпендикулярны.

Источник

Угол между двумя прямыми

Буду кратким. Угол между двумя прямыми равен углу между их направляющими векторами. Таким образом, если вам удастся найти координаты направляющих векторов a = (x₁; y₁; z₁) и b = (x₂; y₂; z₂), то сможете найти угол. Точнее, косинус угла по формуле:

Посмотрим, как эта формула работает на конкретных примерах:

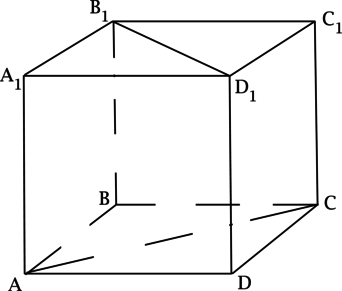
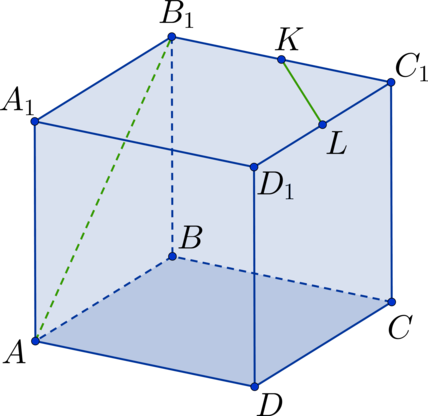
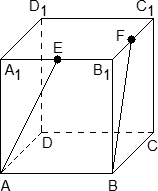
Задача. В кубе ABCDA₁B₁C₁D₁ отмечены точки E и F — середины ребер A₁B₁ и B₁C₁ соответственно. Найдите угол между прямыми AE и BF.

Поскольку ребро куба не указано, положим AB = 1. Введем стандартную систему координат: начало в точке A, оси x, y, z направим вдоль AB, AD и AA₁ соответственно. Единичный отрезок равен AB = 1. Теперь найдем координаты направляющих векторов для наших прямых.

Найдем координаты вектора AE. Для этого нам потребуются точки A = (0; 0; 0) и E = (0,5; 0; 1). Поскольку точка E — середина отрезка A₁B₁, ее координаты равны среднему арифметическому координат концов. Заметим, что начало вектора AE совпадает с началом координат, поэтому AE = (0,5; 0; 1).

Теперь разберемся с вектором BF. Аналогично, разбираем точки B = (1; 0; 0) и F = (1; 0,5; 1), т.к. F — середина отрезка B₁C₁. Имеем:
BF = (1 − 1; 0,5 − 0; 1 − 0) = (0; 0,5; 1).

Итак, направляющие векторы готовы. Косинус угла между прямыми — это косинус угла между направляющими векторами, поэтому имеем:

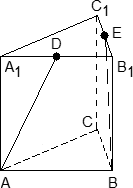
Задача. В правильной трехгранной призме ABCA₁B₁C₁, все ребра которой равны 1, отмечены точки D и E — середины ребер A₁B₁ и B₁C₁ соответственно. Найдите угол между прямыми AD и BE.

Введем стандартную систему координат: начало координат в точке A, ось x направим вдоль AB, z — вдоль AA₁. Ось y направим так, чтобы плоскость OXY совпадала с плоскостью ABC. Единичный отрезок равен AB = 1. Найдем координаты направляющих векторов для искомых прямых.

Для начала найдем координаты вектора AD. Рассмотрим точки: A = (0; 0; 0) и D = (0,5; 0; 1), т.к. D — середина отрезка A₁B₁. Поскольку начало вектора AD совпадает с началом координат, получаем AD = (0,5; 0; 1).

Теперь найдем координаты вектора BE. Точка B = (1; 0; 0) считается легко. С точкой E — серединой отрезка C₁B₁ — чуть сложнее. Имеем:

Осталось найти косинус угла:

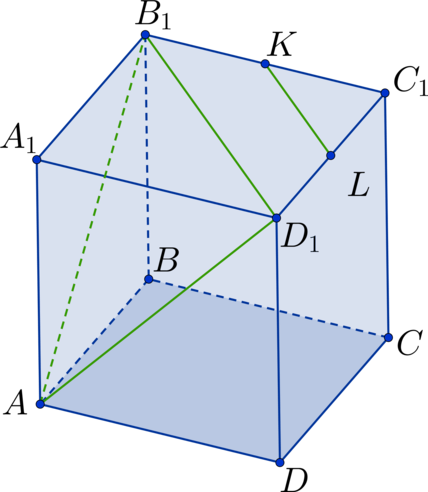
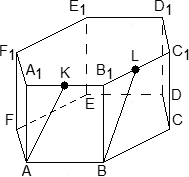
Задача. В правильной шестигранной призме ABCDEFA₁B₁C₁D₁E₁F₁, все ребра которой равны 1, отмечены точки K и L — середины ребер A₁B₁ и B₁C₁ соответственно. Найдите угол между прямыми AK и BL.

Введем стандартную для призмы систему координат: начало координат поместим в центр нижнего основания, ось x направим вдоль FC, ось y — через середины отрезков AB и DE, а ось z — вертикально вверх. Единичный отрезок снова равен AB = 1. Выпишем координаты интересующих нас точек:

Точки K и L — середины отрезков A₁B₁ и B₁C₁ соответственно, поэтому их координаты находятся через среднее арифметическое. Зная точки, найдем координаты направляющих векторов AK и BL:

Теперь найдем косинус угла:

Задача. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, отмечены точки E и F — середины сторон SB и SC соответственно. Найдите угол между прямыми AE и BF.

Введем стандартную систему координат: начало в точке A, оси x и y направим вдоль AB и AD соответственно, а ось z направим вертикально вверх. Единичный отрезок равен AB = 1.

Точки E и F — середины отрезков SB и SC соответственно, поэтому их координаты находятся как среднее арифметическое концов. Выпишем координаты интересующих нас точек:
A = (0; 0; 0); B = (1; 0; 0)

Зная точки, найдем координаты направляющих векторов AE и BF:

Координаты вектора AE совпадают с координатами точки E, поскольку точка A — начало координат. Осталось найти косинус угла:

Источник