Как находится масштаб в физике

Масштаб в математике

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Понятие масштаба

Чтобы понять, что такое масштаб в математике нужно вспомнить тему отношений чисел и пропорций.

Масштаб — это дробь, где в числителе единица, а в знаменателе то число, которое показывает во сколько раз уменьшено расстояние на плане местности, чем на самой местности.

Другими словами, масштабом называют отношение длины отрезка на карте к длине соответствующего отрезка на местности.

Масштаб бывает трех видов:

Курсы обучения математике помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Определение масштаба на карте

На математике в 6 классе обязательно будут задания, как найти масштаб карты. Разберемся в этом вопросе.

Нужно потратить очень много сил, чтобы изобразить дом в натуральную величину, поэтому и придумали такой инструмент, как масштаб. Ведь намного проще описать большой объект в рисунке, чертеже или макете.

Масштаб — это отношение размера изображения к размеру изображаемого объекта.

Масштаб карты — это отношение длины отрезка на карте к его действительной длине на местности.

На карте Российской Федерации указан масштаб (1 : 500 000). Читается это так: карта сделана в масштабе одна пятисот тысячная. Такой масштаб значит, что в 1 см на карте помещается 500 000 см реального расстояния. То есть отрезок на изображении в 1 см соответствует отрезку на местности в 5 км. А если взять отрезок в 3 см, то на местности этот отрезок составит 15 км.

Численные масштабы карт и соответствующие им масштабы на местности:

Масштаб 1 : 100 000

Масштаб 1 : 10000

Масштаб 1 : 5000

Масштаб 1 : 2000

Масштаб 1 : 1000

Масштаб 1 : 500

Масштаб 1 : 200

Масштаб 1 : 100

Решение задач на масштаб

Для закрепления темы решим несколько математических задач на масштаб за 6 класс.

Пример 1. Длина отрезка на карте равна 8 см. Найти длину соответствующего отрезка на местности, если масштаб карты равен 1 : 10 000.

8 * 10 000 = 80 000 (см) — это 10 000 частей

Пример 2. Расстояние между двумя городами 400 км. Найти длину отрезка, который соединяет эти города на карте, выполненный в масштабе 1:5000000.

400 км = 400 000 м = 40 000 000 см

40000000 : 5000000 = 40 : 5 = 8

Пример 3. Расстояние от Москвы до Санкт-Петербурга по прямой составляет примерно 635 км. По автотрассе протяженность маршрута 700 км. Во сколько раз надо уменьшить это расстояние, чтобы его можно было изобразить в виде отрезка длиной в 14 см?

Источник

Как находится масштаб в физике

В экспериментальной физике графиками пользуются для разных целей. Во-первых, графики строят, чтобы определить некоторые величины, – обычно наклон или отрезок, отсекаемый на оси координат, прямой, изображающей зависимость между двумя переменными. Хотя в элементарных курсах физики упор часто делается именно на это, на самом деле роль графика здесь сравнительно невелика. Ведь при методе наименьших квадратов наклон прямой определяют, конечно, не по графикам, как таковым, а по исходным числовым данным. Непосредственно же по графику определить наклон можно только в том случае, если провести через точки на глаз наилучшую прямую. Это довольно грубый метод. Его не следует сбрасывать со счета, но он пригоден лишь тогда, когда мы оценивает результат, полученный наиболее точным методом или когда наклон кривой не очень важен для окончательного результата.

Во-вторых, и это, пожалуй, самое главное, – графиками пользуются для наглядности. Допустим, например, что мы измеряем скорость течения воды по трубке как функцию перепада давления с целью определить, когда поток перестает быть ламинарным и становится турбулентным.

Полученные данные приведены в таблице 1.

Пока поток остается ламинарным, скорость его пропорциональна перепаду давления. Глядя на цифры, приведенные в таблице, трудно сказать, где пропорциональность начинает нарушаться.

Другое дело, когда те же данные, представлены графиком (рис.2). В этом случае сразу видна точка, в которой нарушается пропорциональность.

Графики позволяют также более наглядно проводить сравнение экспериментальных данных с теоретической кривой. Нанося результаты измерений на график, очень удобно следить за тем, как идет эксперимент.

В-третьих, графиками пользуются в экспериментальной работе, чтобы установить эмпирическое соотношение между двумя величинами. Например, градуируя свой термометр по какому-либо образцовому прибору, мы определяем поправку как функцию показаний термометра, (см. рис.3). На графике через полученные точки проводим плавную кривую ( рис.4), которой и пользуемся для введения поправки в показаниях термометра.

§ 2. Масштаб

В физике на графиках принято по горизонтальной оси откладывать независимую переменную, т.е. величину, значение которой задает сам экспериментатор, а по вертикальной оси – ту величину, которую он при этом определяет. Короче говоря, по горизонтали откладывается «причина», а по вертикали – «следствие».

Существуют различные виды бумаги для графиков, но из них в физике наиболее употребительны два: с обычным линейным масштабом (миллиметровая) и логарифмическая. Последняя бывает двух видов: полулогарифмическая, когда логарифмический масштаб взят только на одной оси координат, и двойная логарифмическая, когда такой масштаб удобно использовать для изображения изучаемой величины, изменяющейся на несколько порядков в пределах измерений. Полулогарифмическая бумага удобна в том случае, когда связь между переменными логарифмическая или экспоненциальная (y = B_o + B₁e kx ). Если же эта связь имеет вид y

Рис.5. Неудачный выбор масштаба.

Рис.6 Более удачный выбор масштаба

§ 3. Единицы измерения

§ 4. Как строить графики

Графики делают в основном для того, чтобы наглядно представить результаты эксперимента, и потому они должны быть предельно ясными. Ниже мы дадим ряд общих советов по вычерчиванию графиков. Пользоваться ими нужно с учетом особенностей каждого конкретного случая.

Рис.8 – пример неудачного графика, на котором экспериментальные точки очень мелкие и не отличаются от расчетных точек, по которым проведена теоретическая кривая.

Рис.9 – расчетные точки не видны, а экспериментальные точки четко выделяются.

Полезно иногда через экспериментальные точки проводить «наилучшую» плавную кривую. Обратите внимание на слово плавную. Начинающие нередко соединяют экспериментальные точки просто ломаной линией, как показано на рис.10.

Но тем самым как бы указывается, что соотношение между двумя величинами носит скачкообразный характер, а это, вообще говоря, весьма маловероятно. Скорее следует ожидать, что данное соотношение описывается какой-либо плавной кривой (рис.11),

Рис.10.	Рис.11

а отклонения точек вызваны«шумом» эксперимента, случайными ошибками при измерениях.

Если на графике имеется теоретическая кривая, то «плавную» кривую через экспериментальные точки лучше не проводить. Такая кривая, может быть, не совсем соответствует фактическим данным, и тогда она будет мешать прямому сравнению эксперимента с теорией.

Если с масштабом и расположением точек все в порядке, то нетрудно обвести все тушью или чернилами и сделать жирные экспериментальные точки. В результате вам удастся избежать переделок и лишних затрат графической бумаги. По окончании построения пишут заголовок, который должен содержать краткое и точное содержание того, что показывает график.

§ 5. Как указывать ошибки

Ошибку в экспериментальном значении можно указать следующим образом:

Экспериментальная точка находится в середине отрезка, изображающего величину ошибки. Поскольку нанесение таких значков – дополнительный труд и приводит к усложнению графика, это следует делать лишь в том случае, когда без такой информации обойтись нельзя, т.е. когда от ошибок может зависеть значимость отклонения экспериментальных данных от теоретической кривой (см. рис.12 и 13)

Рис.12.	Рис.13

Отклонения экспериментальных точек от прямой линии на обоих графиках одинаковы, но на рис.12 отклонения вряд ли значимы, а на рис.13, по-видимому, значимы.

Ошибки обычно указывают и еще в одном случае, – когда они неодинаковы для разных экспериментальных точек.

Источник

Фізика – легко!

Вивчаємо фізику та не тільки

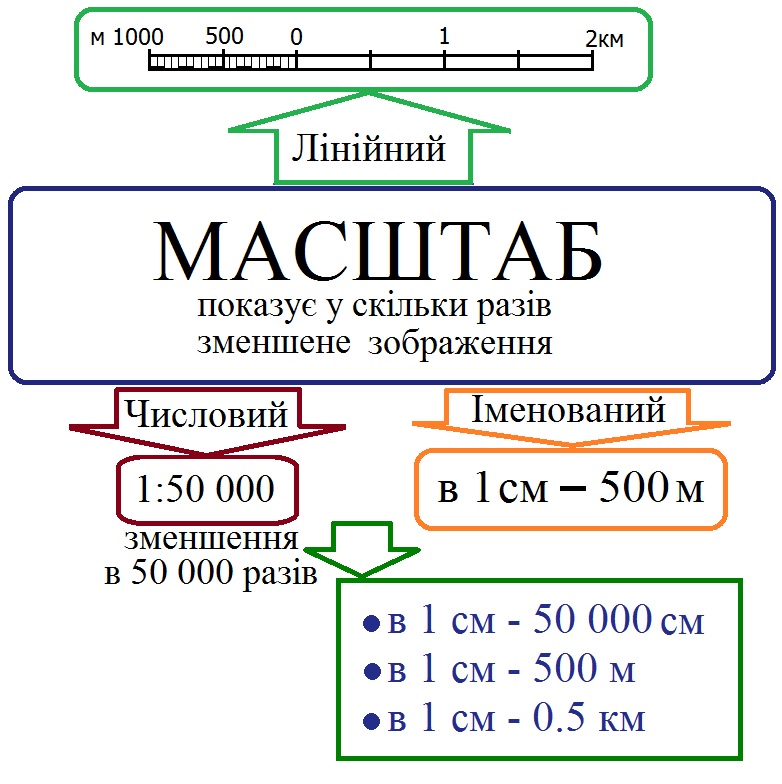
Масштаб

Масштаб – це відношення, яке показує, у скільки разів зменшено зображення на карті (плані, кресленні, глобусі) проти його реальних розмірів на Землі. Тобто масштаб показує скільки сантиметрів на місцевості міститься в 1 см на карті.

Масштаб 1:100 000 показує, що кожному сантиметру на карті відповідає 100 000см (або 1 км) на місцевості (1 км = 100 000 см).
Чим у меншу кількість разів місцевість зменшена під час зображення її на папері, тим більшим є масштаб зображення, і навпаки.

Наприклад, масштаб 1: 10 000 буде більшим, ніж масштаб 1: 350 000, тому що в першому випадку в 1 см – 100 м, а в другому – в 1 см – 3,5 км. Очевидно, що на великому масштабі місцевість буде зображена більш детально.

За масштабом карти класифікують на:

1. оглядові – масштаб більший за 1 : 1 000 000;
2. оглядово-топографічні – від 1 : 1 000 000 до 1 : 500 000;
3. дрібномасштабні – від 1 : 200 000 до 1 : 100 000;
4. середньомасштабні – від 1 : 50 000 до 1 : 25 000;
5. крупномасштабні – від 1 : 10 000 до 1 : 5000, загальногеографічні карти такого масштабу називають топографічними ;
6. топографічні плани – від 1 : 2000 до 1 : 500.

За формою масштаби класифікують:

Запам’ятай! 1 км = 100 000 м; 1м = 100 см

Розв’язання задач

Задача 1

Масштаб карти 1:30 000, а відстань на карті між містами 45 см. Знайдіть реальну відстань між містами на місцевості.

Розв’язання.
Зрозуміло, що відстань на місцевості буде більшою за відстань на карті в 30 000 разів. Тоді 45 см × 30 000 = 1 350 000 см = 13, 5 км

Тобто ми збільшуємо відстань в 30 000 разів

Відповідь : реальна відстань між містами на місцевості 13,5 км.

Задача 2

Відстань між двома містами біля 360 км. Якою буде відстань між містами на карті, якщо масштаб цієї карти 1:300 000?

Розв’язання.
Зрозуміло, що відстань на карті буде менша за відстань на реальній місцевості в
3 000 000 разів.
360 км = 36 000 000 см.
Тоді 36 000 000 см : 3000 000 = 12 см.
Тобто ми зменшуємо реальну відстань в 3 000 000 разів

Відповідь : відстань між містами на карті 12 см.

Задача 3

Відстань між двома містами 750 км. Знайдіть масштаб карти, якщо на ній відстань між цими містами 15 см.

Розв’язання.

750 км = 75 000 000 см
Оскільки масштаб показує у скільки разів зменшено зображення на карті в порівнянні з його реальними розмірами на місцевості, тоді

75 000 000 см : 15 см = 5 000 000.

Відповідь : масштаб карти 1:5 000 000.

Залишити відповідь Скасувати відповідь

Щоб відправити коментар вам необхідно авторизуватись.

Источник

Масштаб

Понятие наиболее распространено в геодезии, картографии и проектировании — отношение натуральной величины объекта к величине его изображения. Человек не в состоянии изобразить большие объекты, например, дом, в натуральную величину, поэтому, при изображении большого объекта в рисунке, чертеже, макете и так далее, человек уменьшает величину объекта в несколько раз: в два, пять, десять, сто, тысяча и так далее. Число, показывающее, во сколько раз уменьшен изображенный объект, есть масштаб. Масштаб применяется и при изображении микромира. Человек не может изобразить живую клетку, которую рассматривает в микроскоп, в натуральную величину и поэтому увеличивает величину ее изображения в несколько раз. Число, показывающее, во сколько раз произведено увеличение или уменьшение реального явления при его изображении, определено как масштаб.

Содержание

Масштаб в геодезии, картографии и проектировании

Масштаб показывает, во сколько раз каждая линия, нанесенная на карту или чертёж, меньше или больше её действительных размеров. Есть три вида масштаба: численный, именованный, графический.

Масштабы на картах и планах могут быть представлены численно или графически.

Численный масштаб записывают в виде дроби, в числителе которой стоит единица, а в знаменателе — степень уменьшения проекции. Например, масштаб 1:5 000 показывает, что 1 см на плане соответствует 5 000 см (50 м) на местности.

Более крупным является тот масштаб, у которого знаменатель меньше. Например, масштаб 1:1 000 крупнее, чем масштаб 1:25 000.

Графические масштабы подразделяются на линейные и поперечные. Линейный масштаб — это графический масштаб в виде масштабной линейки, разделённой на равные части. Поперечный масштаб — это графический масштаб в виде номограммы, построение которой основано на пропорциональности отрезков параллельных прямых, пересекающих стороны угла.Поперечный масштаб применяют для более точных измерений длин линий на планах. Поперечным масштабом пользуются следующим образом: откладывают на нижней линии поперечного масштаба замер длины таким образом, чтобы один конец (правый) был на целом делении ОМ, а левый заходил за 0. Если левая ножка попадает между десятыми делениями левого отрезка (от 0), то поднимаем обе ножки измерителя вверх, пока левая ножка не попадёт на пересечение к-либо трансвенсали и какой-либо горизонтальной линии. При этом правая ножка измерителя должна находиться на этой же горизонтальной линии. Наименьшая ЦД = 0,2 мм, а точность — 0,1.

Точность масштаба — это отрезок горизонтального проложения линии, соответствующий 0,1 мм на плане. Значение 0,1 мм для определения точности масштаба принято из-за того, что это минимальный отрезок, который человек может различить невооруженным глазом. Например, для масштаба 1:10 000 точность масштаба будет равна 1 м. В этом масштабе 1 см на плане соответствует 10 000 см (100 м) на местности, 1 мм — 1 000 см (10 м), 0,1 мм — 100 см (1 м).

Масштабы изображений на чертежах должны выбираться из следующего ряда: [1]

При проектировании генеральных планов крупных объектов допускается применять масштабы 1:2 000; 1:5 000; 1:10 000; 1:20 000; 1:25 000; 1:50 000.
В необходимых случаях допускается применять масштабы увеличения (100n):1, где n — целое число.

Масштаб в фотографии

При фотосъёмке под масштабом понимают отношение линейного размера изображения, полученного на фотоплёнке или светочувствительной матрице, к линейному размеру проекции соответствующей части сцены на плоскость, перпендикулярную к направлению на камеру.

Некоторые фотографы измеряют масштаб как отношение размеров объекта к размерам его изображения на бумаге, экране или ином носителе. Правильная методика определения масштаба зависит от контекста, в котором используется изображение.

Масштаб имеет важное значение при расчете глубины резко изображаемого пространства. Фотографам доступен очень широкий диапазон масштабов — от практически бесконечно малого (например, при съемке небесных тел) до очень крупного (без использования специальной оптики возможно получение масштабов порядка 10:1).

Под макрофотографией традиционно понимают съёмку в масштабе 1:1 или крупнее. Однако с широким распространением компактных цифровых фотоаппаратов этим термином стали также называть съёмку расположенных близко к объективу (как правило, ближе 50 см) мелких объектов. Связано это с необходимым изменением режима работы системы автофокуса в таких условиях, однако с точки зрения классического определения макросъёмки такое толкование является неверным.

Масштаб в моделизме

Для каждого вида масштабного (стендового) моделизма определены масштабные ряды, состоящие из нескольких масштабов разной степени уменьшения, причём для разных видов моделизма (авиамоделизм, судомоделизм, железнодорожный, автомобильный, военной техники) определены свои, исторически сложившиеся, масштабные ряды, которые обычно не пересекаются.

Масштаб в моделизме исчисляется по формуле:

При масштабе 1/72, и параметре оригинала 7500 мм, решение будет выглядеть;

7500 мм / 72 = 104,1 мм

Полученное значение 104,1 мм, есть искомое значение при масштабе 1/72

Масштаб времени

В программировании

В операционных системах с разделением времени чрезвычайно важную роль играет предоставление отдельно взятым задачам так называемого «режима реального времени», при котором обработка внешних событий обеспечивается без дополнительных задержек и пропусков. Для этого употребляется также термин «реальный масштаб времени», однако это терминологическая условность, не имеющая к исходному значению слова «масштаб» никакого отношения.

В кинотехнике

Масштаб времени — количественная мера замедления или ускорения движения, равная отношению проекционной частоты кадров к съёмочной. Так, если проекционная частота кадров равна 24 кадра в секунду, а киносъёмка производилась на 72 кадра в секунду, масштаб времени равен 1:3. Масштаб времени 2:1 означает ускоренное вдвое по сравнению с обычным протекание процесса на экране.

В математике

Масштабы изображений на чертежах должны выбираться из следующего ряда (масштабы ГОСТ 2.302-68): Масштабы уменьшения 1 : 2; 1 : 2,5; 1 : 4; 1 : 5; 1 : 10; 1 : 15; 1 : 20; 1 : 25; 1 : 40; 1 : 50; 1 : 75; 1 : 100; 1 : 200; 1 : 400; 1 : 500; 1 : 800; 1 : 1000 Натуральная величина 1 : 1 Масштабы увеличения 2 : 1; 2.5,5 : 1; 4 : 1; 5 : 1; 10 : 1; 20 : 1; 40 : 1; 50 : 1; 100: 1 см. например Быстро-медленная система

Масштаб-число,показывающее, во сколько раз уменьшены или увеличены настоящие размеры на чертеже.

Источник

Масштаб и математика

Понятие масштаб тесно связано с отношением чисел и пропорциями. Поэтому, если вы не уверены в своих знаниях по этим темам, настоятельно рекомендуем изучить их еще раз.

Вы можете сделать это и на нашем ресурсе в темах отношение чисел и пропорции.

Масштаб — важное понятие. Если вы научитесь его правильно понимать, он поможет вам не только в математике, но и в географии, черчении, а порой и в физике.

Масштабом называют отношение длины отрезка на карте к длине соответствующего отрезка на местности (в реальности).

Разберёмся на примере:

Ниже представлена часть карты с масштабом 1 : 10 000 000 (см). Такой масштаб означает, что в 1 см на карте помещается 10 000 000 (см) реального расстояния, или 100 000 (м), или 100 (км).

Санкт-Петербург и Москва на карте соединены отрезком длиной в 6,5 (см).

Определим, сколько в реальности (км) между Москвой и Санкт-Петербургом.

Для решения этой задачи составим таблицу и занесём в неё нужные данные. Неизвестную величину обозначим за « x ».

Составим и решим пропорцию:

Ответ: 650 км — приблизительное расстояние между Москвой и Санкт-Петербургом.

Теперь, зная, что такое масштаб, вы легко с помощью линейки можете измерить расстояние на карте или на чертеже и рассчитать нужное расстояние в реальности.

Источник