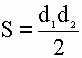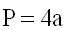Как находится площадь ромба формула
Как рассчитать площадь ромба
На данной странице калькулятор поможет рассчитать площадь ромба онлайн. Для расчета задайте длину основания, высоту или длины диагоналей и угол между ними.
Ромб – четырёхугольник, у которого все стороны равны между собой. Ромб является частным случаем параллелограмма. Ромб с прямыми углами называется квадратом.
Через сторону и высоту
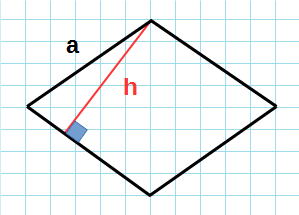
Формула для нахождения площади ромба через сторону и высоту:
Через диагонали
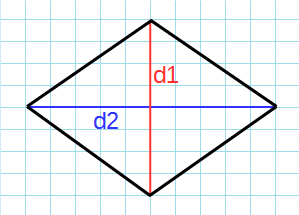
Формула для нахождения площади ромба через диагонали:
Через сторону и угол
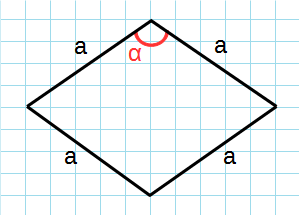
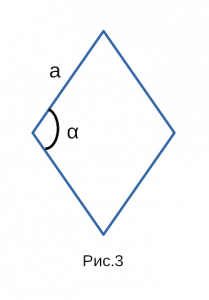
Формула для нахождения площади ромба через сторону и угол:
Через угол и диагональ из этого угла
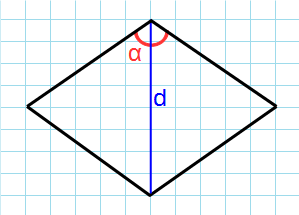
Формула для нахождения площади ромба через угол и диагональ выходящая из этого угла:
Через угол и противолежащию диагональ
Формула для нахождения площади ромба через угол и диагональ противолежащая углу:
Через угол и радиус вписанной окружности
Формула для нахождения площади ромба через угол и радиус вписанной окружности:
Как найти площадь ромба
Площадь ромба можно вычислить разными способами.
Например, через половину произведения двух диагоналей
друг на друга, через синус и сторону в квадрате…
Также, площадь ромба равна площади параллелограмма.
Как следствие, так, как ромб является параллелограммом, с
равными сторонами, поэтому площадь ромба
можно найти через площадь параллелограмма.
Для ромба истинны и верны все свойства параллелограмма.
Формула площади ромба и формула
площади параллелограмма одинаковая.
Ромб — параллелограмм, у которого
все четыре стороны равны.
Формулировка площади ромба через параллелограмм:
Формула площади ромба через параллелограмм:
a — основание; h — высота;
Площадь ромба, можно также найти другим способом. Для
этого мысленно разделим ромба на четыре треугольника,
так чтобы каждая вершина была соединена с противоположной
вершиной. Получившиеся линии называют диагоналями. Если
известны длины двух диагоналей ромба, то можно найти площадь.
Формула площади ромба через две диагонали:
d1 и d2 — диагонали;
В самых редких случаях, если известен синус и одна из сторон,
используют формулу площади ромба через синус и квадрат стороны.
Формулировка площади ромба через синус и сторону в квадрате:
Формула площади ромба через синус и сторону в квадрате:
a — сторона; sin α — синус угла;
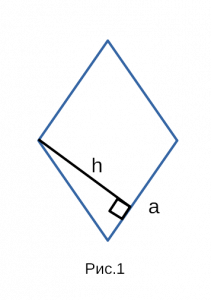
Рис. 1 — площадь ромба через площадь параллелограмма / основание и высоту.
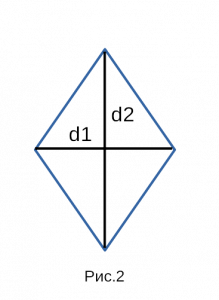
Рис. 2 — площадь ромба через две диагонали
Рис. 3 — площадь ромба через синус и сторону в квадрате
Также, вы можете прочитать про свойства и признаки ромба.
Формулы ромба
Формулы площади ромба:
1) Площадь ромба равна произведению длины его стороны на высоту (a, h).
2) Площадь ромба равна половине произведения его диагоналей.
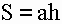
Формула периметра ромба:
1) Периметр ромба равен сумме 4-х длин его сторон или произведению длины любой его стороны на четыре (так как у ромба длины всех сторон равны).
Остались вопросы?
Здесь вы найдете ответы.
Высота ромба представляет собой перпендикуляр, который опущен из одного из его углов на сторону, противоположную данному углу.
Обозначим имеющийся ромб как ABCD. Из его угла В проведем высоту ВН, после чего получим треугольник АВН с прямым углом. Известно, что длина всех сторон ромба одинаковая, а длина АН равна половине длины АВ. Зная это и используя теорему, которая является обратной теореме о 30-градусном угле, можно провести доказательство того, что угол АВН равен 30 градусам.
Учитывая то, что сумма всех углов треугольника равна 180 градусом, можно найти неизвестную величину третьего угла треугольника:
Так, угол АВС равен:
Известна формула площади (S) ромба, которая представляет собой произведение длины его стороны (а) на высоту (h), проведенную к ней:
Есть возможность выразить высоту из приведенной выше формулы. Она будет равна отношению площади ромба к длине его стороны:
Площадь (S) треугольника с прямым углом рассчитывается путем деления пополам произведения длин его катетов. В данном случае она будет равна:
Площадь ромба определяется умножением длины его стороны на высоту, проведенную к ней. Если принять высоту за х, и учесть, что площадь ромба равна площади прямоугольного треугольника (6 см.кв.), то:
Отсюда можно найти значение х:
Ответ: высота ромба составляет 1,2 см.
Диагонали, проведенные в ромбе, делят эту фигуру на четыре треугольника, которые являются равными. Длины катетов этих треугольников составляют 3 см. и 4 см. Такой вывод можно сделать на основании того, что в точке пересечения диагоналей они делятся пополам. Гипотенуза (с) треугольников представляет собой сторону ромба. Ее длина равна:
Следовательно, сторона ромба также равна 5 см.
Площадь ромба высчитывается как произведение длин его диагоналей, деленное пополам:
S = d1*d2/2 = 6*8/2 = 24 см. кв.
Известна также другая формула, используемая для вычисления площади ромба, в которой длина его стороны (а) умножается на высоту(h):
Из данной формулы выражаем высоту:
Ответ: Высота ромба составляет 4,8 см.
Высоту ромба можно рассчитать, если его диагонали (d1 и d2)и сторона (а) – известные величинами. В этом случае для определения неизвестной высоты следует пользоваться приведенной ниже формулой:
Периметр (Р) ромба равен сумме длин всех его сторон (а) и вычисляется по следующей формуле:
В данном случае периметр ромба равен 48 см., это значит, что:
Находим значение а:
Площадь ромба (S) является произведением длины его стороны (а) и высоты (h), проведенной к этой стороне:
В задании сказано, что площадь ромба – 60 см.кв. Значит:
Находим неизвестную высоту:
Ответ: Высота ромба – 5 см.
Согласно формуле расчета периметра (Р) ромба, он равен сумме длин всех его сторон (а) (Р=а+а+а+а). Известно, что все стороны ромба имеет одинаковую длину. Из этого следует, что длина одной стороны будет равна ¼ части его периметра:
Площадь (S) ромба можно высчитать путем умножения длины его стороны (а) на высоту (h), проведенную к ней:
В конкретном случае:
Отсюда можем найти высоту (h), разделив площадь на длину стороны ромба:
Ответ: Высота ромба составляет 6 см.
Периметр (Р) ромба равен сумме длин всех его сторон (а), длины которых равны. Это значит:
Предположим, что длина одной из диагоналей ромба равна 10х, тогда длина второй его диагонали будет выглядеть как 24х. Отношение их длин можно записать в следующем виде:
Доказано, что диагонали ромба взаимно перпендикулярны и в точке пересечения они делятся пополам, при этом образуя четыре равных треугольника с прямым углом.
Теорема Пифагора гласит, что сумма длин его катетов, возведенных во вторую степень, равна длине гипотенузы, которая также возведена в квадрат:
Для данной задачи это равенство записывается так:
169х²=169; следовательно, х2 = 1. Значит х тоже будет равен 1.
Длина диаметра, обозначенного как 10х, равна 10 см. (10*1), а длина второго диаметра, который обозначен как 24х, равна 24 см. (24*1).
Площадь (S) ромба рассчитывается как:
Из этого можно составить следующее уравнение:
Выражаем h и получаем:
h= d₁*d₂/2*а=10·24:26=240/26=120/13 см.
Ромб имеет четыре высоты. Все они имеют равные длины. Вывод об этом можно сделать, рассмотрев все треугольные фигуры, элементами которых являются эти высоты. Есть возожность высчитать высоту ромба при помощи различных параметров, которые могут быть указаны в условии конкретной задачи.
Предположим, что нам известна площадь (S) ромба и длина его стороны (а). В этом случае высота ромба будет равна отношению его площади к длине высоты: h = S/a.
Если же по условию задачи известны длины диагоналей ромба d1 и d2, а также его сторона а, то высоту можно рассчитать так: h = (d1*d2 )/a.
В случае, когда известна длина стороны (а) ромба и угол А, находящийся между смежными сторонами, то для расчета высоты ромба используется следующая формула:
h = a*a*sin A /a = a*sin A.
Существуют также и другие варианты вычисления длины высоты ромба на основании того, какие величины будут известны по условию задания. Однако ключевыми параметрами, используя которые можно вычислить высоту ромба, являются диагонали, длина любой его стороны и угол, образованный между смежными сторонами.
Площадь ромба можно рассчитать одним из трех способов:
1. S = a² sin a, в которой α — образованный двумя сторонами угол, a — сторона.
2. S = ah, или Длина стороны ромба, умноженная на его высоту.
3. S = (d1*d2)/2, в которой d1 и d2 – длины диагоналей фигуры.
Зная, чему равен периметр ромба, можно вычислить длину его стороны:
Известно, что высота данной фигуры меньше ее стороны на 1,7 см. Теперь можем определить длину высоты:
Площадь ромба можно найти, умножив его сторону на высоту, которая на нее опущена:
Ответ: S = 50,4 см. кв.
Если длины диагоналей фигуры относятся как 4/3, то их половины будут относиться также:
(4d)²+(3d)²=10² = 16d²+9d² = 100
Теперь можно найти площадь:
S= 2*d¹/2*d²/2=2*8*6 = 96 см.кв.
Ответ: S ромба = 96 см.кв.
Площадь ромба можно описать как сумму площадей 2-х треугольных фигур, основанием которых является одна диагональ, а вторая диагональ ромба представляет собой сумму длин высот этих фигур. Диагонали ромба при пересечении образуют угол в 90 градусов. На основании этого можно найти площадь ромба следующим образом:
Известно, что, пересекаясь, диагонали ромба образуют угол в 90 градусов и в точке пересечения делятся пополам.
Для расчета площади ромба через диагонали нужно перемножить их длины, а затем разделить полученное число на два:
Для примера можно рассмотреть ромб, одна диагональ которого равна 5 см., а вторая – 4 см. Тогда его площадь будет равна:
S ромба возможно вычислить, перемножив длину одной из его сторон (а) и высоту (h). Формула записывается так:
Формулы ромба не по зубам? Тебе ответит эксперт через 10 минут!
Площадь ромба онлайн
С помощю этого онлайн калькулятора ромба можно найти площадь ромба по известным элементам. Для нахождения площади ромба введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть смотрите ниже.
| Открыть онлайн калькулятор |
1. Площадь ромба через сторону и угол
Пусть задан ромб ABCD (Рис.1). Выведем формулу вычисления площади ромба через сторону и угол.
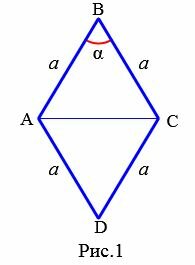 |
Проведем диагональ AC. Тогда ромб делится на два треугольника ABC и ADC. Противолежащие углы ромба равны (свойство 1 статя Ромб). Поэтому треугольники ABC и ADC равны по двум сторонам и углу между ними. Площадь треугольника ABC по двум сторонам и углу между ними вычисляется по формуле:
или, учитывая, что AB=BC=a:
Аналогично, площадь треугольника ADC вычисляется по формуле
Поэтому площадь ромба равна:
2. Площадь ромба через диагонали
Пусть известны диагонали d1 и d2 ромба ABCD (Рис.2). Выведем формулу вычисления площади ромба через диагонали.
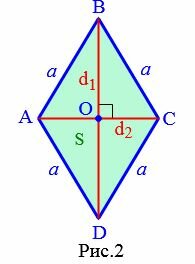 |
Поскольку диагонали ромба перепендикулярны и точкой пересечения делятся пополам (свойства 6 и 5 ромба), то они разделяют ромб на четыре прямоугольных треугольника. Тогда эти прямоугольные треугольники равны по двум катетам: \( \small \frac
Тогда площадь ромба равна:
3. Площадь ромба через сторону и высоту
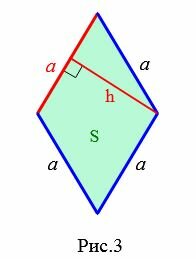 |
Пусть известны сторона a и высота h ромба (Рис.3). Так как ромб является параллелограммом, то площадь ромба вычисляется по формуле площади параллелограмма:
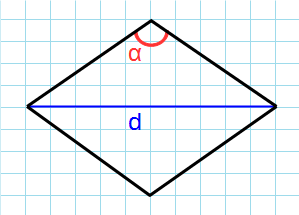
4. Площадь ромба через угол и противолежащую диагональ
Пусть известны один из углов α=∠ABC ромба и противолежащий диагональ d=AC (Рис.4). Выведем формулу вычисления площади ромба.
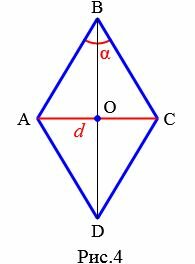 |
Проведем другой диагональ BD. Как было отмечено в параграфе 2, диагонали ромба разделяют его на четыре равных прямоугольных треугольников. Найдем площадь одного из них:
или, учитывая что \( \small AO=\frac<\large d><\large 2>,\) получим:
Тогда площадь ромба равна:
5. Площадь ромба через угол и диагональ из данного угла
Пусть известны один из углов α=∠BAD ромба и диагональ из данного угла d=AC (Рис.5). Выведем формулу вычисления площади ромба.
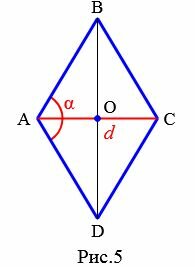 |
Проведем другой диагональ BD. Как было отмечено в параграфе 2, диагонали ромба разделяют его на четыре равных прямоугольных треугольников. Найдем площадь одного из них:
или, учитывая что \( \small AO=\frac<\large d><\large 2>,\) получим:
Тогда площадь ромба равна:
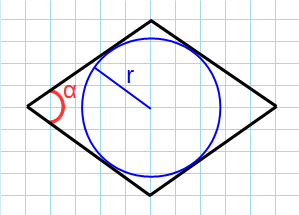
6. Площадь ромба через угол и радиус вписанной в ромб окружности
Пусть известны один из углов α=∠ABC ромба и радиус r вписанной в ромб окружности (Рис.6). Выведем формулу вычисления площади ромба.
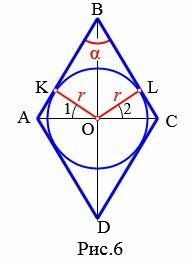 |
Как мы отметили выше, диагонали разделяют ромб на четыре равных прямоугольных треугольника. В частности
Тогда \( \small \angle BAO=\angle BCO=90°-\frac< \large \alpha > <\large 2>\). Треугольники AKO и CLO также прямоугольные. Следовательно
Применим теорему синусов для прямоугольного треугольника AOB:
Для прямоугольного треугольника AKO имеем:
или, учитывая (12) и KO=r:
Подставляя (15) в (14), получим:
Найдем площадь треугольника AOB:
Подставляя (15) и (16) в (17), получим:
Тогда площадь ромба равна:
7. Площадь ромба через сторону и радиус вписанной в ромб окружности
Пусть известны сторона a=AB ромба и радиус r вписанной в ромб окружности (Рис.7). Найдем площадь ромба.
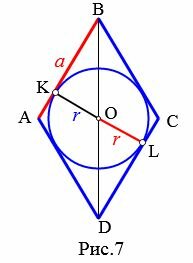 |
Прямая AB является касательной к окружности вписанной в ромб. Тогда \( \small OK ⊥ AB \). Прямая CD является касательной к окружности вписанной в ромб. Тогда \( \small OL ⊥ CD \). Поэтому треугольники BKO и DLO прямоугольные. Эти треугольники равны по гипотенузе и катету (BO=OD, KO=OL). Тогда \( \small \angle BOK=\angle DOL \). Углы BOK и KOD смежные. Следовательно \( \small \angle KOD=180°-\angle BOK. \) \( \small \angle KOD+\angle DOL \) \( \small =180°-\angle BOK+\angle DOL=180°. \) Получили, что отрезки KO и OL находятся на одной прямой. То есть KL=KO+OL=2r. Поскольку \( \small KL ⊥ AB, \) то является высотой ромба. Площадь ромба по стороне и высоте вычисляется из формулы (3). Тогда имеем:
Ромб. Формулы, признаки и свойства ромба
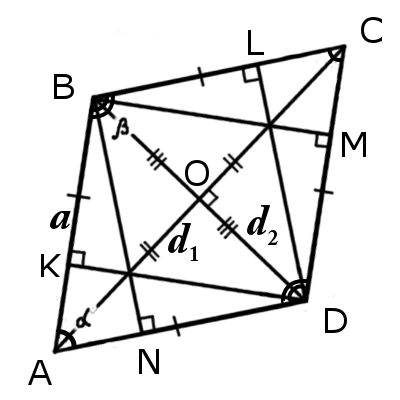 | 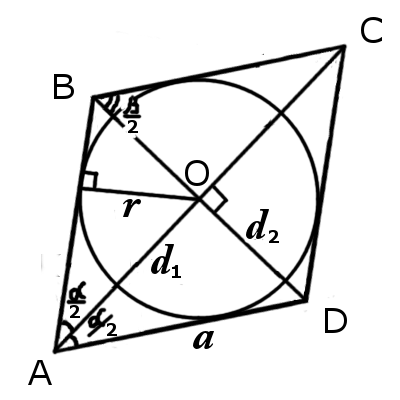 |
| Рис.1 | Рис.2 |
Признаки ромба
∠BAC = ∠CAD или ∠BDA = ∠BDC
Δ ABO = Δ BCO = Δ CDO = Δ ADO
Основные свойства ромба
∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC
Сторона ромба
Формулы определения длины стороны ромба:
2. Формула стороны ромба через площадь и синус угла:
| a = | √ S |
| √ sinα |
| a = | √ S |
| √ sinβ |
3. Формула стороны ромба через площадь и радиус вписанной окружности:
| a = | S |
| 2 r |
6. Формула стороны ромба через большую диагональ и половинный угол:
| a = | d 1 |
| 2 cos ( α /2) |
| a = | d 1 |
| 2 sin ( β /2) |
7. Формула стороны ромба через малую диагональ и половинный угол:
| a = | d 2 |
| 2 cos ( β /2) |
| a = | d 2 |
| 2 sin ( α /2) |
Диагонали ромба
Формулы определения длины диагонали ромба:
d 1 = a √ 2 + 2 · cosα
d 2 = a √ 2 + 2 · cosβ
d 1 = 2 a · cos ( α /2)
d 1 = 2 a · sin ( β /2)
d 2 = 2 a · sin ( α /2)
d 2 = 2 a · cos ( β /2)
7. Формулы диагоналей через площадь и другую диагональ:
| d 1 = | 2S |
| d 2 |
| d 2 = | 2S |
| d 1 |
8. Формулы диагоналей через синус половинного угла и радиус вписанной окружности:
| d 1 = | 2 r |
| sin ( α /2) |
| d 2 = | 2 r |
| sin ( β /2) |
Периметр ромба
Периметром ромба называется сумма длин всех сторон ромба.
Длину стороны ромба можно найти за формулами указанными выше.
Формула определения длины периметра ромба:
Площадь ромба
Формулы определения площади ромба:
4. Формула площади ромба через две диагонали:
5. Формула площади ромба через синус угла и радиус вписанной окружности:
6. Формулы площади через большую диагональ и тангенс острого угла ( tgα ) или малую диагональ и тангенс тупого угла ( tgβ ):
| S = | 1 | d 1 2 · tg ( α /2) |
| 2 |
| S = | 1 | d 2 2 · tg ( β /2) |
| 2 |
Окружность вписанная в ромб
Формулы определения радиуса круга вписанного в ромб:
1. Формула радиуса круга вписанного в ромб через высоту ромба:
2. Формула радиуса круга вписанного в ромб через площадь и сторону ромба:
3. Формула радиуса круга вписанного в ромб через площадь и синус угла:
4. Формулы радиуса круга вписанного в ромб через сторону и синус любого угла:
| r = | a · sinα |
| 2 |
| r = | a · sinβ |
| 2 |
5. Формулы радиуса круга вписанного в ромб через диагональ и синус угла:
| r = | d 1 · sin ( α /2) |
| 2 |
| r = | d 2 · sin ( β /2) |
| 2 |
6. Формула радиуса круга вписанного в ромб через две диагонали:
| r = | d 1 · d 2 |
| 2√ d 1 2 + d 2 2 |
7. Формула радиуса круга вписанного в ромб через две диагонали и сторону:
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.