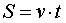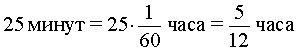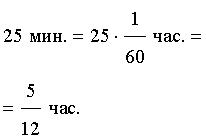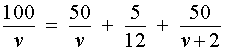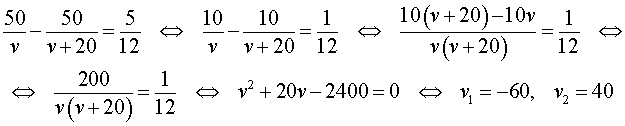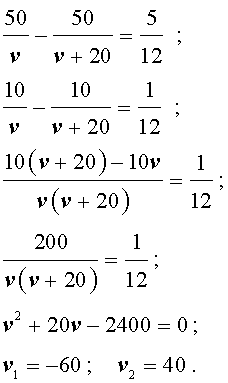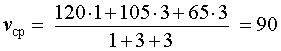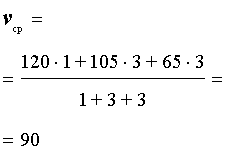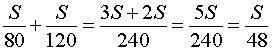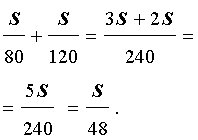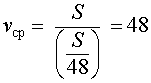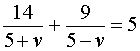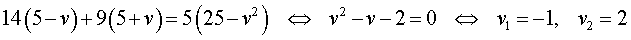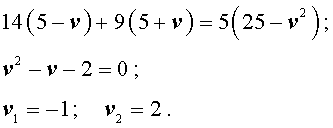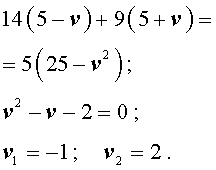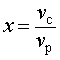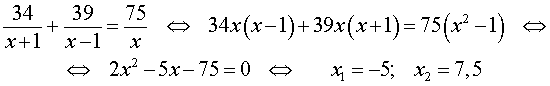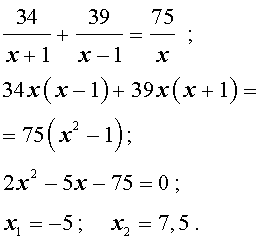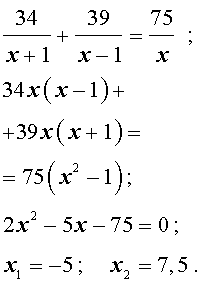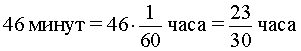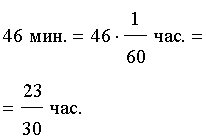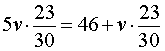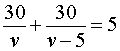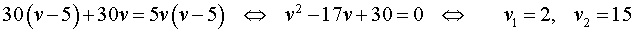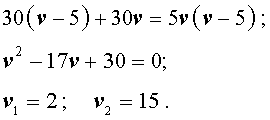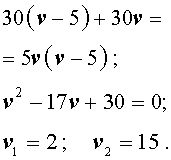Как находится собственная скорость лодки

Как находится собственная скорость лодки

Пн-Пт 9:00-19:00
Сб-Вс 10:00-16:00

Как рассчитать по формулам скорость лодки?

Собрали для Вас актуальные формулы, которые могут оказаться полезными каждому

✓ Формула 1

На примере разберем, как находить скорость лодки.

Скорость лодки по течению 21,8км/ч, а против течения 17,2 км/ч. Найти собственную скорость лодки и скорость течения реки.

Решение: Согласно формулам: Vс=(Vпо теч.+Vпр теч.)/2 и Vтеч.=(Vпо теч. — Vпр. теч)/2, найдем:

Vтеч = (21,8 — 17,2)/2=4,6\2=2,3 (км/ч)

Vс = Vпр теч.+Vтеч=17,2+2,3=19,5 (км/ч)

Ответ: Vc=19,5 (км/ч), Vтеч=2,3 (км/ч).

✓ Формула 2

Самым простым методом самостоятельного расчета предельной скорости лодки считается использование формулы, учитывающей параметры двигателя.

Для этого используется формула вычисления двигателя V = NK/R, где искомый параметр V – скорость километров в час, R – сопротивление движению (его вы можете взять в технической документации своего катера), K – коэффициент полезной деятельности винта. Определяется он в зависимости от типа лодки. Так, для спортивного катера его значение — 160, для крупных винтов — 140, для средних и малых — 120 и 100 соответственно.

Параметр N – мощность работы двигателя катера. Эту информацию вы можете рассчитать самостоятельно или обратиться за помощью к технической документации. Для того, чтобы вычислить предел скорости катера, возьмите максимально допустимую мощность. Этот метод позволяет рассчитать предел максимальной скорости катера достаточно точно, однако не следует забывать про вероятную погрешность.

Возможно вам будет интересным

История производства подвесных лодочных моторов

С чего все началось? Рассказываем!

15 сентября 2020 433

Что такое виндсерфинг и зачем он нужен?

Подробнее рассказываем в нашей статье!

31 августа 2020 354

Этапы получения прав на маломерное судно

Получение любых прав на средства передвижения требуют определенных затрат, например: сбор необходимых документов, обучение, экзамены и многое другое. Рассказываем подробнее.

27 августа 2020 454

В чем плюсы бронирования лодок ПВХ?

Рассказываем особенности, читайте

20 августа 2020 384

5 мифов про лодки ПВХ

Таинственные лодки ПВХ и какие мифы их окружают?

17 августа 2020 360

Почему покупают детские велосипеды?

Хотите порадовать ребенка велосипедом? Отлично, наш ассортимент полон детских велосипедов!

10 августа 2020 348

Что нужно знать перед покупкой велосипеда?

Какие бывают велосипеды? Как выбрать? Читайте в статье

Как выбрать лодочный мотор?

Отвечаем на Вопросы наших покупателей

Что такое килеватость судна и на что влияет?

Читайте подробнее в статье!

14 июля 2020 1 031

Пункт выдачи заказов:
г. Санкт-Петербург, ул. Софийская д. 8к1 БЦ Крол

Пн-Сб 10:00-19:00
Вс 10:00-18:00

Остались вопросы?

Задайте их нам прямо сейчас!

© Море Моторов, 2021 | Все права защищены

Предложения, размещенные на сайте more-motorov.ru, не являются публичной офертой

Пожалуйста, введите Ваши данные, и менеджер свяжется с Вами в ближайшее время

Источник

Как найти скорость в стоячей воде

Первое, что необходимо выучить и знать «на зубок» – формулы. Запишите и запомните:

Vпр. теч=Vпо теч. – 2Vтеч.

Vпо теч.=Vпр. теч+2Vтеч.

Vтеч.=(Vпо теч. – Vпр. теч)/2

Vс=(Vпо теч.+Vпр теч.)/2 или Vс=Vпо теч.+Vтеч.

На примере разберем, как находить собственную скорость и решать задачи такого типа.

Пример 1.Скорость лодки по течению 21,8км/ч, а против течения 17,2 км/ч. Найти собственную скорость лодки и скорость течения реки.

Решение: Согласно формулам: Vс=(Vпо теч.+Vпр теч.)/2 и Vтеч.=(Vпо теч. – Vпр. теч)/2, найдем:

Vтеч = (21,8 – 17,2)/2=4,62=2,3 (км/ч)

Vс = Vпр теч.+Vтеч=17,2+2,3=19,5 (км/ч)

Ответ: Vc=19,5 (км/ч), Vтеч=2,3 (км/ч).

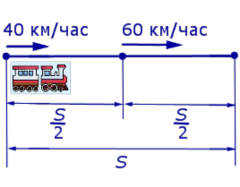
Пример 2. Пароход прошел против течения 24 км и вернулся обратно, затратив на обратный путь на 20 мин меньше, чем при движении против течения. Найдите его собственную скорость в неподвижной воде, если скорость течения равна 3 км/ч.

За Х примем собственную скорость парохода. Составим таблицу, куда занесем все данные.

Против теч. По течению

Зная, что на обратный путь пароход затратил на 20 минут времени меньше, чем на путь по течению, составим и решим уравнение.

Х=21(км/ч) – собственная скорость парохода.

Ответ или решение 1

Скорость лодки плывущей по течению реки, будет больше скорости лодки плывущей в стоячей воде, на скорость этого самого течения. Потому что, течение помогает лодке плыть. Следовательно чтобы узнать скорость лодки в стоячей воде, необходимо от скорости лодки плывущей по течению вычесть скорость течения реки. Узнаем собственную скорость лодки, если, нам известно что ее скорость по течению 19,2 км в час, а скорость течения 2,6 км в час.

19,2 – 2,6 = 16,6 км в час.

Ответ: Скорость лодки в стоячей воде составляет 16,6 км в час.

Разделы: Математика

Данный материал представляет собой систему задач по теме “Движение”.

Цель: помочь учащимся более полно овладеть технологиями решения задач по данной теме.

Задачи на движение по воде.

Очень часто человеку приходится совершать движения по воде: реке, озеру, морю.

Сначала он это делал сам, потом появились плоты, лодки, парусные корабли. С развитием техники пароходы, теплоходы, атомоходы пришли на помощь человеку. И всегда его интересовали длина пути и время, затраченное на его преодоление.

Представим себе, что на улице весна. Солнце растопило снег. Появились лужицы и побежали ручьи. Сделаем два бумажных кораблика и пустим один из них в лужу, а второй – в ручей. Что же произойдет с каждым из корабликов?

В луже кораблик будет стоять на месте, а в ручейке – поплывет, так как вода в нем «бежит» к более низкому месту и несет его с собой. То же самое будет происходить с плотом или лодкой.

В озере они будут стоять на месте, а в реке – плыть.

Рассмотрим первый вариант: лужа и озеро. Вода в них не движется и называется стоячей.

Кораблик поплывет по луже только в том случае, если мы его подтолкнем или если подует ветер. А лодка начнет двигаться в озере при помощи весел или если она оснащена мотором, то есть за счет своей скорости. Такое движение называют движением в стоячей воде.

Отличается ли оно от движения по дороге? Ответ: нет. А это значит, что мы с вами знаем как действовать в этом случае.

Задача 1. Скорость катера по озеру равна 16 км/ч.

Какой путь пройдет катер за 3 часа?

Следует запомнить, что скорость катера в стоячей воде называют собственной скоростью.

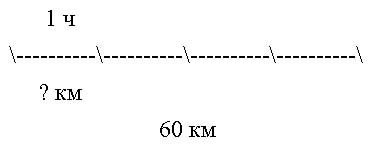
Задача 2. Моторная лодка за 4 часа проплыла по озеру 60 км.

Найдите собственную скорость моторной лодки.

Задача 3. Сколько времени потребуется лодке, собственная скорость которой

равна 28 км/ч, чтобы проплыть по озеру 84 км?

Итак, чтобы найти длину пройденного пути, необходимо скорость умножить на время.

Чтобы найти скорость, необходимо длину пути разделить на время.

Чтобы найти время, необходимо длину пути разделить на скорость.

Чем же отличается движение по озеру от движения по реке?

Вспомним бумажный кораблик в ручье. Он плыл, потому что вода в нем движется.

Такое движение называют движением по течению. А в обратную сторону – движением против течения.

Итак, вода в реке движется, а значит имеет свою скорость. И называют ее скоростью течения реки. ( Как ее измерить?)

Задача 4. Скорость течения реки равна 2 км/ч. На сколько километров река относит

любой предмет (щепку, плот, лодку) за 1час, за 4 часа?

Каждый из вас плавал в реке и помнит, что по течению плыть гораздо легче, чем против течения. Почему? Потому, что в одну сторону река «помогает» плыть, а в другую – «мешает».

Те же, кто не умеет плавать, могут представить себе ситуацию, когда дует сильный ветер. Рассмотрим два случая:

1) ветер дует в спину,

2) ветер дует в лицо.

И в том и в другом случае идти сложно. Ветер в спину заставляет бежать, а значит, скорость нашего движения увеличивается. Ветер в лицо сбивает нас, притормаживает. Скорость при этом уменьшается.

Остановимся на движении по течению реки. Мы уже говорили о бумажном кораблике в весеннем ручье. Вода понесет его вместе с собой. И лодка, спущенная на воду, поплывет со скоростью течения. Но если у нее есть собственная скорость, то она поплывет еще быстрее.

Следовательно, чтобы найти скорость движения по течению реки, необходимо сложить собственную скорость лодки и скорость течения.

Задача 5. Собственная скорость катера равна 21 км/ч, а скорость течения реки 4 км/ч. Найдите скорость катера по течению реки.

Теперь представим себе, что лодка должна плыть против течения реки. Без мотора или хотя бы весел, течение отнесет ее в обратную сторону. Но, если придать лодке собственную скорость ( завести мотор или посадить гребца), течение будет продолжать отталкивать ее назад и мешать двигаться вперед со своей скоростью.

Поэтому, чтобы найти скорость лодки против течения, необходимо из собственной скорости вычесть скорость течения.

Задача 6. Скорость течения реки равна 3 км/ч, а собственная скорость катера 17 км/ч.

Найдите скорость катера против течения.

Задача 7. Собственная скорость теплохода равна 47,2 км/ч, а скорость течения реки 4,7 км/ч. Найдите скорость теплохода по течению и против течения.

Ответ: 51,9 км/ч; 42,5 км/ч.

Задача 8. Скорость моторной лодки по течению равна12,4 км/ч. Найдите собственную скорость лодки, если скорость течения реки 2,8 км/ч.

Задача 9. Скорость катера против течения равна 10,6 км/ч. Найдите собственную скорость катера и скорость по течению, если скорость течения реки 2,7 км/ч.

Ответ: 13,3 км/ч; 16 км/ч.

Связь между скоростью по течению и скоростью против течения.

Введем следующие обозначения:

V_с. – собственная скорость,

V_теч. – скорость течения,

V _{по теч.} – скорость по течению,

V _пр.теч. – скорость против течения.

Тогда можно записать следующие формулы:

Попытаемся изобразить это графически:

Вывод: разность скоростей по течению и против течения равна удвоенной скорости течения.

Vno теч — Vnp. теч = 2 Vтеч.

Vтеч = (V по теч – Vnp. теч ): 2

1) Скорость катера против течения равна 23 км/ч, а скорость течения 4 км/ч.

Найдите скорость катера по течению.

2) Скорость моторной лодки по течению реки равна 14 км/ч/ а скорость течения 3 км/ч. Найдите скорость лодки против течения

Задача 10. Определите скорости и заполните таблицу:

Источник

Особенности решения задач на определение скорости течения реки. Примеры решений

Одними из увлекательных задач по математике и физике, которые предлагает учитель решить школьникам, являются задачи на определение скорости течения реки. В данной статье рассмотрим особенности решения этих задач и приведем несколько конкретных примеров.

О каких задачах пойдет речь?

Каждый знает, что вода в реке обладает некоторой скоростью течения. Равнинные реки (Дон, Волга) текут относительно медленно, небольшие же горные реки отличаются сильным течением и присутствием водяных воронок. Любой плавающий предмет, который брошен в реку, будет удаляться от наблюдателя со скоростью течения реки.

Люди, которые купались в реке, знают, что против ее течения плыть очень тяжело. Чтобы продвинуться на несколько метров, необходимо приложить намного больше усилий, чем при движении в стоячей воде озера. Наоборот, движение по течению осуществляется практически без каких-либо затрат энергии. Достаточно лишь поддерживать тело на плаву.

Все эти особенности позволяют сделать следующий важный вывод: если тело, имеющее в стоячей воде скорость v, будет двигаться в русле реки, то его скорость относительно берега будет равна:

Если тело движется под некоторым углом к течению, то результирующий вектор его скорости будет равен сумме векторов v¯ и u¯.

Формулы, которые необходимо запомнить

Помимо приведенной выше информации, для решения задач на скорость течения реки следует запомнить несколько формул. Перечислим их.

Скорость течения является величиной постоянной, а вот скорость тела (лодки, катера, пловца) в общем случае может меняться, как по величине, так и по направлению. Для равномерного прямолинейного движения справедливой будет формула:

Помимо этих формул, для успешного решения задач следует уметь пользоваться тригонометрическими функциями при разложении векторов скорости на составляющие.

Теперь перейдем к решению конкретных задач.

Задача с лодкой и рыбаком

Один рыбак решил отправиться на своей лодке без мотора вверх против течения реки на расстояние 2 километра. В стоячей воде он бы преодолел это расстояние за 30 минут, но при движении по реке ему понадобился целый час. Необходимо найти, чему равна скорость течения реки.

Поскольку скорость воды в реке является величиной неизвестной, то обозначим ее буквой x. Скорость лодки также неизвестна, однако ее можно вычислить, используя значения из условия для движения в стоячей воде. Получаем для скорости v лодки:

Мы нашли скорость, с которой рыбак на лодке может перемещаться по спокойному озеру. Чтобы найти скорость лодки против течения, необходимо из найденной величины вычесть значение x. Тогда для движения вверх по реке можно записать следующее равенство:

Выражаем отсюда значение неизвестного параметра, имеем:

Осталось подставить цифры из условия задачи и записать ответ:

Таким образом, скорость течения в реке в два раза меньше таковой для лодки.

Задача с моторной лодкой

Моторная лодка совершает каждый день переходы по реке из пункта A в пункт B. Дистанция между A и B составляет 7 км. Известно, что скорость лодки по течению равна 8 км/ч. Чему равна скорость течения, если на путь вниз по реке лодка затрачивает на 10 минут больше времени, чем при движении вверх по ней.

В данном случае мы не знаем ни скорость моторной лодки, ни скорость воды в реке. Обозначим первую как y, а вторую как x. Тогда можно записать следующие четыре уравнения:

Первое уравнение отражает скорость лодки по течению, второе и третье уравнения связывают время и скорость при движении вниз и вверх по реке соответственно. Четвертое уравнение следует из условия задачи о разности времен прямого и обратного пути между пунктами A и B.

Сначала найдем из этих уравнений время t₁ и t₂:

Для определения скорости x воды в реке вычтем из второго третье уравнение, получим:

Подставляем в это равенство рассчитанные величины t₁ и t₂, а также расстояние между пунктами S, получаем, что вода в реке течет со скоростью 0,64 км/ч.

Задача: движение катера под углом к течению

Теперь решим задачу, которая требует умения пользоваться тригонометрическими формулами.

Катер начал движение от одного берега реки к другому под углом 60 o к течению. Скорость катера в стоячей воде равна 10 км/ч. Скорость течения составляет 2 км/ч. Необходимо определить, на какое расстояние катер сместится вдоль берега, прибыв на противоположную сторону реки. Ширина русла реки равна 500 метров.

Данную задачу следует решать, разбив путь катера на две составляющие: перпендикулярную и параллельную берегу. Используя данные задачи, для перпендикулярной составляющей пути можно записать выражение:

Для вычисления параллельного берегу пути S₂ к горизонтальной проекции скорости катера следует добавить скорость течения, тогда соответствующее равенство будет иметь вид:

Подставляя известные величины, получаем ответ: катер вдоль берега пройдет путь 404 метра.

Источник

Как найти собственную скорость лодки

В задачах «на движение по реке» присутствуют скорости: собственная скорость (Vс), скорость по течению (Vпо теч.), скорость против течения (Vпр. теч.), скорость течения (Vтеч.). Необходимо отметить, что собственная скорость водного суда – это скорость в стоячей воде. Чтобы найти скорость по течению, надо к скорости течения прибавить собственную. Для того чтобы найти скорость против течения, надо из собственной скорости вычесть скорость течения.

Vпо теч.=Vпр. теч+2Vтеч.

Vс=(Vпо теч.+Vпр теч.)/2 или Vс=Vпо теч.+Vтеч.

На примере разберем, как находить собственную скорость и решать задачи такого типа.

Пример 1.Скорость лодки по течению 21,8км/ч, а против течения 17,2 км/ч. Найти собственную скорость лодки и скорость течения реки.

Vс = Vпр теч.+Vтеч=17,2+2,3=19,5 (км/ч)

Ответ: Vc=19,5 (км/ч), Vтеч=2,3 (км/ч).

Пример 2. Пароход прошел против течения 24 км и вернулся обратно, затратив на обратный путь на 20 мин меньше, чем при движении против течения. Найдите его собственную скорость в неподвижной воде, если скорость течения равна 3 км/ч.

За Х примем собственную скорость парохода. Составим таблицу, куда занесем все данные.

Против теч. По течению

Зная, что на обратный путь пароход затратил на 20 минут времени меньше, чем на путь по течению, составим и решим уравнение.

Х=21(км/ч) – собственная скорость парохода.

Источник

Задачи на движение

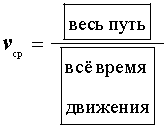
Скорость тела. Средняя скорость тела

Решение задач на движение опирается на хорошо известную из курса физики формулу

Сразу же сделаем важное

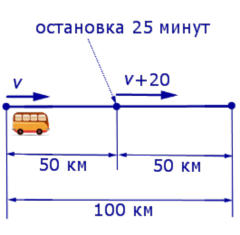
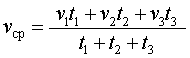(2)

– время движения автобуса по расписанию (в часах);

– время, за которое автобус проехал первую половину пути (в часах);

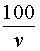
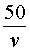
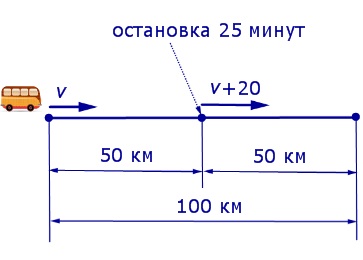
v + 20 – скорость автобуса во второй половине пути (в км/час);

– время, за которое автобус проехал вторую половину пути (в часах).

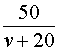
В условии задачи дано время остановки автобуса – 25 минут. Его необходимо выразить в часах, чтобы все единицы измерения были согласованными:

Теперь можно составить уравнение, исходя из того, что автобус прибыл в конечный пункт вовремя, а, значит, время, которое он был в пути, плюс время остановки должно равняться времени движения автобуса по расписанию:

Решим это уравнение:

По смыслу задачи первый корень должен быть отброшен.

Задача 2. (МИОО) Первый час автомобиль ехал со скоростью 120 км/час, следующие три часа – со скоростью 105 км/час, а затем три часа – со скоростью 65 км/час. Найдите среднюю скорость автомобиля на протяжении всего пути.

– время, за которое поезд прошел первую половину пути, выраженное в часах;

– время, за которое поезд прошел вторую половину пути, выраженное в часах.

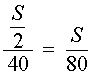
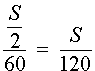
Следовательно, время, за которое поезд прошел весь путь, равно

В соответствии с формулой (1) средняя скорость поезда на протяжении всего пути

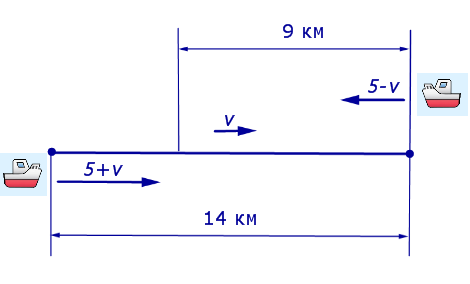
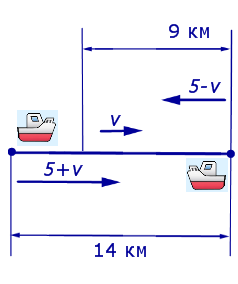
Движение по реке. Скорость течения реки

В отличие от задач на движение по суше, в задачах на движение по реке появляется новая величина – скорость течения реки.

По отношению к берегу, который неподвижен, скорость тела, движущегося по течению реки, равна сумме собственной скорости тела ( скорости тела по озеру, скорости тела в неподвижной воде, скорости тела в стоячей воде ) и скорости течения реки. По отношению к берегу скорость тела, движущегося против течения реки, равна разности собственной скорости тела и скорости течения реки.

5 + v – скорость, с которой лодка шла по течению реки (в км/час);

– время движения лодки по течению реки (в часах);

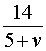
5 – v – скорость, с которой лодка шла против течения реки (в км/час);

– время движения лодки против течения реки (в часах);

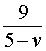
Теперь можно составить уравнение, принимая во внимание тот факт, что лодка находилась в пути 5 часов:

Решим это уравнение:

По смыслу задачи первый корень должен быть отброшен.

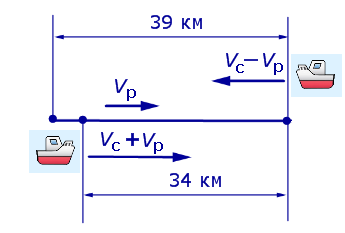
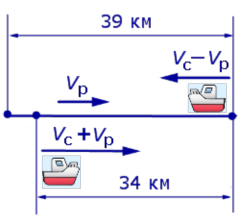
Задача 5. (Бюро «Квантум») Моторная лодка прошла по течению реки 34 км и 39 км против течения, затратив на это столько же времени, сколько ей нужно, чтобы пройти 75 километров в стоячей воде. Найдите отношение скорости лодки в стоячей воде к скорости течения реки.

Учитывая тот факт, что в обеих ситуациях лодка провела в пути одно и то же время, можно составить уравнение:

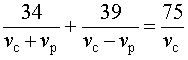(3)

Если ввести обозначение

то, воспользовавшись формулой

перепишем уравнение (3) в виде

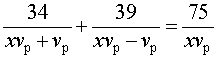(4)

По смыслу задачи первый корень должен быть отброшен.

Движение по кольцевым трассам

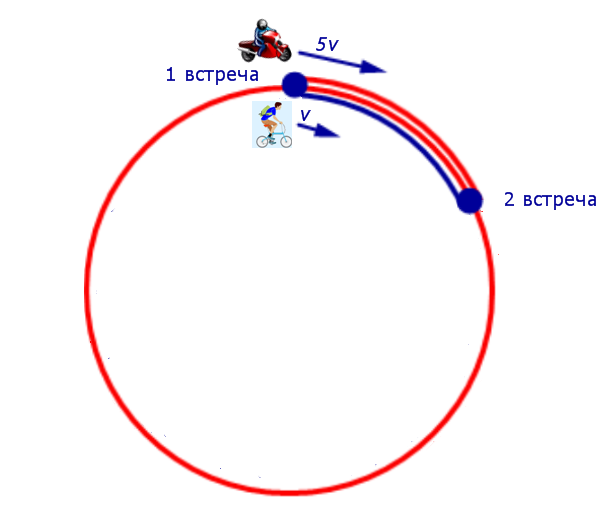
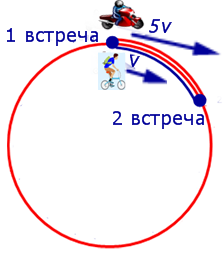
Задача 6. (www.reshuege.ru) Из пункта A круговой трассы длиной 46 км выехал велосипедист, а через 20 минут из пункта A следом за велосипедистом отправился мотоциклист. Через 5 минут после отправления мотоциклист догнал велосипедиста в первый раз, а еще через 46 минут после этого мотоциклист догнал велосипедиста во второй раз. Найдите скорости велосипедиста и мотоциклиста.

Таким образом, обозначив буквой v (км/час) скорость велосипедиста, получаем, что скорость мотоциклиста равна 5v (км/час).

В условии задачи дано время, прошедшее между двумя последовательными встречами мотоциклиста и велосипедиста, – 46 минут. Это время необходимо выразить в часах, чтобы все единицы измерения были согласованными:

Изобразим данные задачи, касающиеся движения мотоциклиста и велосипедиста между первой и второй встречами, на рисунке 6.

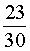
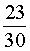
Поскольку за время часа, прошедшее от момента первой встречи до момента второй встречи, мотоциклист проехал 46 км (вся круговая трасса) плюс путь, который проехал велосипедист за часа, то можно составить следующее уравнение:

Решая это уравнение, находим скорость велосипедиста:

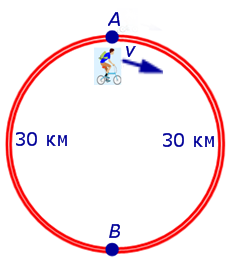
Если обозначить буквой v (км/час) скорость, с которой велосипедист прошел первый круг, то скорость велосипедиста на втором круге будет равна v – 5 (км/час), и можно составить уравнение

Решая это уравнение, находим скорость велосипедиста на первом круге:

Поскольку скорость велосипедиста на первом круге больше, чем 5 км/час, то первый корень должен быть отброшен.

Желающие ознакомиться с примерами решения различных задач по теме «Проценты» и применением процентов в экономике и финансовой математике могут посмотреть разделы нашего справочника «Проценты. Решение задач на проценты», «Простые и сложные проценты. Предоставление кредитов на основе процентной ставки», а также наши учебные пособия «Задачи на проценты» и «Финансовая математика».

Приемы, используемые для решения задач на выполнение работ представлены в разделе нашего справочника «Задачи на выполнение работ».

С примерами решения задач на смеси, сплавы и растворы можно ознакомиться в разделе нашего справочника «Задачи на смеси, сплавы и растворы».

Источник