Как находится собственная скорость теплохода
Как найти скорость в стоячей воде
Первое, что необходимо выучить и знать «на зубок» – формулы. Запишите и запомните:
Vпр. теч=Vпо теч. – 2Vтеч.
Vпо теч.=Vпр. теч+2Vтеч.
Vтеч.=(Vпо теч. – Vпр. теч)/2
Vс=(Vпо теч.+Vпр теч.)/2 или Vс=Vпо теч.+Vтеч.
На примере разберем, как находить собственную скорость и решать задачи такого типа.
Пример 1.Скорость лодки по течению 21,8км/ч, а против течения 17,2 км/ч. Найти собственную скорость лодки и скорость течения реки.
Решение: Согласно формулам: Vс=(Vпо теч.+Vпр теч.)/2 и Vтеч.=(Vпо теч. – Vпр. теч)/2, найдем:
Vтеч = (21,8 – 17,2)/2=4,62=2,3 (км/ч)
Vс = Vпр теч.+Vтеч=17,2+2,3=19,5 (км/ч)
Ответ: Vc=19,5 (км/ч), Vтеч=2,3 (км/ч).
Пример 2. Пароход прошел против течения 24 км и вернулся обратно, затратив на обратный путь на 20 мин меньше, чем при движении против течения. Найдите его собственную скорость в неподвижной воде, если скорость течения равна 3 км/ч.
За Х примем собственную скорость парохода. Составим таблицу, куда занесем все данные.
Против теч. По течению
Зная, что на обратный путь пароход затратил на 20 минут времени меньше, чем на путь по течению, составим и решим уравнение.
Х=21(км/ч) – собственная скорость парохода.
Ответ или решение 1
Скорость лодки плывущей по течению реки, будет больше скорости лодки плывущей в стоячей воде, на скорость этого самого течения. Потому что, течение помогает лодке плыть. Следовательно чтобы узнать скорость лодки в стоячей воде, необходимо от скорости лодки плывущей по течению вычесть скорость течения реки. Узнаем собственную скорость лодки, если, нам известно что ее скорость по течению 19,2 км в час, а скорость течения 2,6 км в час.
19,2 – 2,6 = 16,6 км в час.
Ответ: Скорость лодки в стоячей воде составляет 16,6 км в час.
Разделы: Математика
Данный материал представляет собой систему задач по теме “Движение”.
Цель: помочь учащимся более полно овладеть технологиями решения задач по данной теме.
Задачи на движение по воде.
Очень часто человеку приходится совершать движения по воде: реке, озеру, морю.
Сначала он это делал сам, потом появились плоты, лодки, парусные корабли. С развитием техники пароходы, теплоходы, атомоходы пришли на помощь человеку. И всегда его интересовали длина пути и время, затраченное на его преодоление.
Представим себе, что на улице весна. Солнце растопило снег. Появились лужицы и побежали ручьи. Сделаем два бумажных кораблика и пустим один из них в лужу, а второй – в ручей. Что же произойдет с каждым из корабликов?
В луже кораблик будет стоять на месте, а в ручейке – поплывет, так как вода в нем «бежит» к более низкому месту и несет его с собой. То же самое будет происходить с плотом или лодкой.
В озере они будут стоять на месте, а в реке – плыть.
Рассмотрим первый вариант: лужа и озеро. Вода в них не движется и называется стоячей.
Кораблик поплывет по луже только в том случае, если мы его подтолкнем или если подует ветер. А лодка начнет двигаться в озере при помощи весел или если она оснащена мотором, то есть за счет своей скорости. Такое движение называют движением в стоячей воде.
Отличается ли оно от движения по дороге? Ответ: нет. А это значит, что мы с вами знаем как действовать в этом случае.
Задача 1. Скорость катера по озеру равна 16 км/ч.
Какой путь пройдет катер за 3 часа?
Следует запомнить, что скорость катера в стоячей воде называют собственной скоростью.
Задача 2. Моторная лодка за 4 часа проплыла по озеру 60 км.
Найдите собственную скорость моторной лодки.
Задача 3. Сколько времени потребуется лодке, собственная скорость которой
равна 28 км/ч, чтобы проплыть по озеру 84 км?
Итак, чтобы найти длину пройденного пути, необходимо скорость умножить на время.
Чтобы найти скорость, необходимо длину пути разделить на время.
Чтобы найти время, необходимо длину пути разделить на скорость.
Чем же отличается движение по озеру от движения по реке?
Вспомним бумажный кораблик в ручье. Он плыл, потому что вода в нем движется.
Такое движение называют движением по течению. А в обратную сторону – движением против течения.
Итак, вода в реке движется, а значит имеет свою скорость. И называют ее скоростью течения реки. ( Как ее измерить?)
Задача 4. Скорость течения реки равна 2 км/ч. На сколько километров река относит
любой предмет (щепку, плот, лодку) за 1час, за 4 часа?
Каждый из вас плавал в реке и помнит, что по течению плыть гораздо легче, чем против течения. Почему? Потому, что в одну сторону река «помогает» плыть, а в другую – «мешает».
Те же, кто не умеет плавать, могут представить себе ситуацию, когда дует сильный ветер. Рассмотрим два случая:
1) ветер дует в спину,
2) ветер дует в лицо.
И в том и в другом случае идти сложно. Ветер в спину заставляет бежать, а значит, скорость нашего движения увеличивается. Ветер в лицо сбивает нас, притормаживает. Скорость при этом уменьшается.
Остановимся на движении по течению реки. Мы уже говорили о бумажном кораблике в весеннем ручье. Вода понесет его вместе с собой. И лодка, спущенная на воду, поплывет со скоростью течения. Но если у нее есть собственная скорость, то она поплывет еще быстрее.
Следовательно, чтобы найти скорость движения по течению реки, необходимо сложить собственную скорость лодки и скорость течения.
Задача 5. Собственная скорость катера равна 21 км/ч, а скорость течения реки 4 км/ч. Найдите скорость катера по течению реки.
Теперь представим себе, что лодка должна плыть против течения реки. Без мотора или хотя бы весел, течение отнесет ее в обратную сторону. Но, если придать лодке собственную скорость ( завести мотор или посадить гребца), течение будет продолжать отталкивать ее назад и мешать двигаться вперед со своей скоростью.
Поэтому, чтобы найти скорость лодки против течения, необходимо из собственной скорости вычесть скорость течения.
Задача 6. Скорость течения реки равна 3 км/ч, а собственная скорость катера 17 км/ч.
Найдите скорость катера против течения.
Задача 7. Собственная скорость теплохода равна 47,2 км/ч, а скорость течения реки 4,7 км/ч. Найдите скорость теплохода по течению и против течения.
Ответ: 51,9 км/ч; 42,5 км/ч.
Задача 8. Скорость моторной лодки по течению равна12,4 км/ч. Найдите собственную скорость лодки, если скорость течения реки 2,8 км/ч.
Задача 9. Скорость катера против течения равна 10,6 км/ч. Найдите собственную скорость катера и скорость по течению, если скорость течения реки 2,7 км/ч.
Ответ: 13,3 км/ч; 16 км/ч.
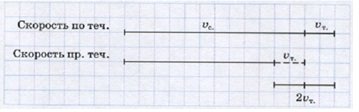
Связь между скоростью по течению и скоростью против течения.
Введем следующие обозначения:
Vс. – собственная скорость,
Vтеч. – скорость течения,
V по теч. – скорость по течению,
V пр.теч. – скорость против течения.
Тогда можно записать следующие формулы:
Попытаемся изобразить это графически:
Вывод: разность скоростей по течению и против течения равна удвоенной скорости течения.
Vno теч — Vnp. теч = 2 Vтеч.
Vтеч = (V по теч – Vnp. теч ): 2
1) Скорость катера против течения равна 23 км/ч, а скорость течения 4 км/ч.
Найдите скорость катера по течению.
2) Скорость моторной лодки по течению реки равна 14 км/ч/ а скорость течения 3 км/ч. Найдите скорость лодки против течения
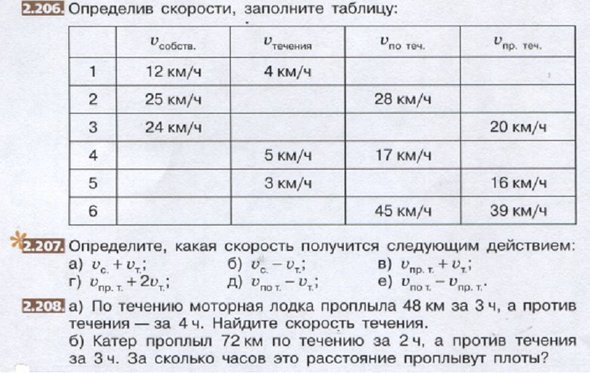
Задача 10. Определите скорости и заполните таблицу:
Задачи на движение по воде
Скорость по течению реки равна сумме собственной скорости транспортного средства и скорости течения реки
Чтобы найти скорость против течения, нужно отнять от собственной скорости транспортного средства скорость течения реки
Для начала необходимо за «х» взять неизвестную. В нашем случае(и чаще всего) за «х» берется скорость.
| $S$(км) | $v$(км/ч) | $t$(ч) |
| По течению | $(x+4)$ | |
| Против течения | $(x-4)$ |
| $S$(км) | $v$(км/ч) | $t$(ч) |
| По течению | $120$ | $(x+4)$ |
| Против течения | $120$ | $(x-4)$ |
| $S$(км) | $v$(км/ч) | $t$(ч) | |
| По течению | $120$ | $(x+4)$ | $<120>/<(х+4)>$ |
| Против течения | $120$ | $(x-4)$ | $<120>/<(х-4)>$ |
Решим полученное дробно рациональное уравнение, для этого перенесем все слагаемые в левую часть.
Далее проговариваем: дробь равна нулю, когда числитель равен нулю, а знаменатель не равен нулю.
Найдем сначала корни знаменателя (ОДЗ дроби)
Найдем корни числителя.
Для этого раскроем скобки и приведем подобные слагаемые.
| $S$(км) | $v$(км/ч) | $t$(ч) | |
| Первый теплоход | $70$ | $x$ | $<70>/<х>$ |
| Второй теплоход | $70$ | $(x+8)$ | $<70>/<(х+8)>$ |
Так как второй теплоход выехал на час позже, то время его в пути на час меньше относительно времени первого теплохода. Составим и решим уравнение: из большего времени отнимаем меньшее время и все это равно разнице времен
Приводим дроби к общему знаменателю
Найдем сначала корни знаменателя(ОДЗ дроби)
Найдем корни числителя
Задачи на движение по реке
Задачи на движение по реке трудны для пятиклассников, а взрослые недоумевают: чего же там трудного? Бревно или плот плывут со скоростью течения реки Vт., которая считается постоянной.
Скорость катера в стоячей воде Vс. называют собственной скоростью катера. Скорость катера по течению реки Vпо теч. больше собственной скорости катера на скорость течения реки: Vпо теч. = Vс. + Vт.
Скорость катера против течения реки Vпр теч. меньше собственной скорости катера на скорость течения реки: Vпо теч. = Vс. + Vт.
Эти соотношения полезно проиллюстрировать рисунком.
Скорость катера по течению больше его скорости против течения на две скорости течения.
Задача 1. Скорость катера в стоячей воде равна 15 км/ч, а скорость течения реки — 3 км/ч. Какова скорость катера по течению и против течения реки?
1) 15 + 3 = 18 (км/ч) — скорость катера по течению реки,
2) 15 — 3 = 12 (км/ч) — скорость катера против течения реки.
Ответ. 18 км/ч и 12 км/ч.
Обратим внимание: скорость катера по течению реки — это сумма его собственной скорости и скорости течения реки, а скорость катера против течения реки— это разность его собственной скорости и скорости течения реки, поэтому скорость по течению реки больше скорости против течения на удвоенную скорость течения.
Задача 2. Скорость моторной лодки по течению реки равна 48 км/ч, а против течения — 42 км/ч. Какова скорость течения реки и собственная скорость моторной лодки?
1) 48 — 42 = 6 (км/ч) — удвоенная скорость течения реки,
2) 6: 2 = 3 (км/ч) — скорость течения реки,
3) 48 — 3 = 45 (км/ч) — собственная скорость.
Ответ. 3 км/ч и 45 км/ч.
Задачи для закрепления берём в учебнике «Математика» для 5 класса (Просвещение, С. М. Никольский и др.) или в книге для учителя «Обучение решению текстовых задач в 5-6 классах» (раздел Книги на сайте www.shevkin.ru). Приведём три задачи из учебника.
В качестве примера применения формируемого умения приведём задачу из сборника для подготовки к ГИА-9.
Задача 3. Теплоход проходит по течению реки до пункта назначения 160 км и после стоянки возвращается в пункт отправления. Найдите скорость течения реки, если скорость теплохода в неподвижной воде равна 18 км/ч, стоянка длится 2 часа, а в пункт отправления теплоход возвращается ровно через 20 часов после отплытия из него.
Составлять и решать уравнение с неизвестным в знаменателе научат в 8 классе, если новый стандарт не отменит изучение таких уравнений, а находить скорость теплохода по течению и против течения реки надо научиться в 5 классе.
Задачи на движение по реке
Рассмотрим задачи, в которых речь идёт о движении объекта по реке. Скорость любого объекта в стоячей воде называют собственной скоростью этого объекта.
Чтобы узнать скорость объекта, который движется против течения реки, надо из собственной скорости объекта вычесть скорость течения реки.
Задача 1. Катер движется против течения реки. За сколько часов он преодолеет расстояние 112 км, если его собственная скорость 30 км/ч, а скорость течения реки 2 км/ч?
Решение: Сначала узнаем скорость движения катера против течения реки, для этого от его собственной скорости отнимем скорость течения:
Теперь можно узнать за сколько часов катер преодолеет 112 км, разделив расстояние на скорость:
Решение задачи по действиям можно записать так:
Ответ: За 4 часа катер преодолеет расстояние 112 км.
Чтобы узнать скорость объекта, который движется по течению реки, надо к собственной скорости объекта прибавить скорость течения реки.
Задача 2. Расстояние от пункта A до пункта B по реке равно 120 км. Сколько времени потратит моторная лодка на путь от пункта A до B, если её собственная скорость 27 км/ч, а скорость течения реки 3 км/ч?
Рассмотрите два варианта:
1) лодка движется по течению реки;
2) лодка движется против течения реки.
Решение: Если моторная лодка будет двигаться по течению реки, то её скорость будет равна сумме собственной скорости со скоростью течения реки:
Значит расстояние между пунктами лодка преодолеет за:
Если лодка будет двигаться против течения реки, то её скорость будет равна разности собственной скорости и скорости течения реки:
Значит, чтобы узнать сколько времени потратит лодка на путь от пункта A до пункта B, надо расстояние разделить на скорость:
Решение задачи по действиям для движения по течению реки можно записать так:
1) 27 + 3 = 30 (км/ч) — скорость лодки,
Для движения против течения реки решение задачи по действиям можно записать так:
1) При движении по течению реки моторная лодка потратит 4 часа на путь от пункта A до пункта B.
2) При движении против течения реки моторная лодка потратит 5 часов на путь от пункта A до пункта B.