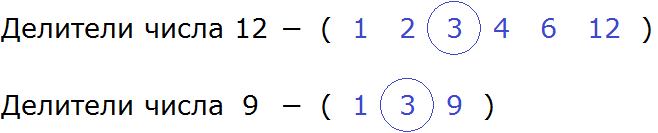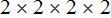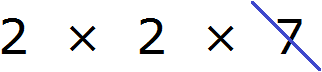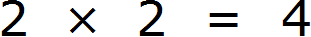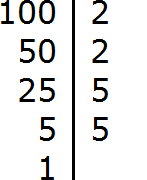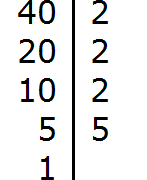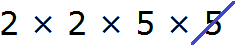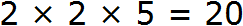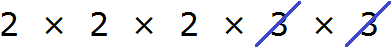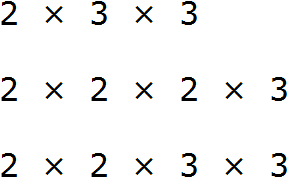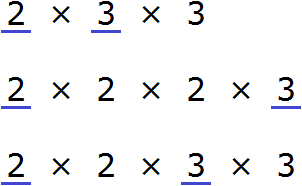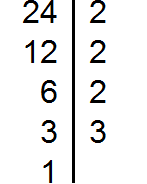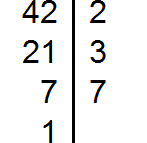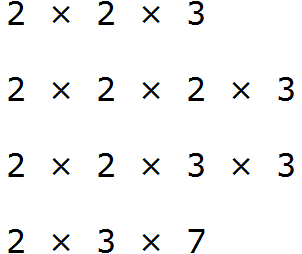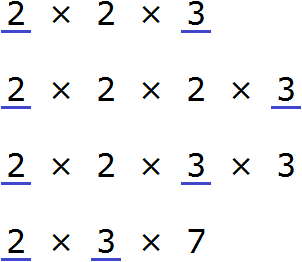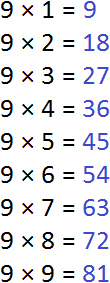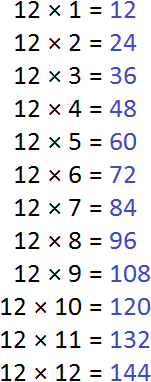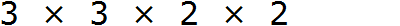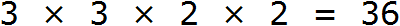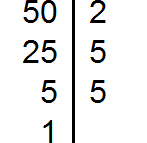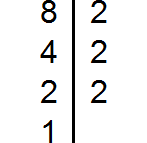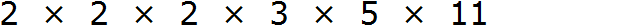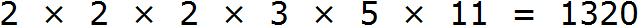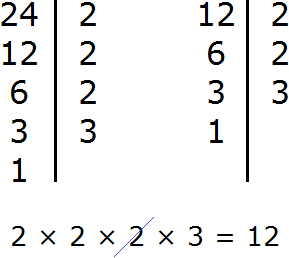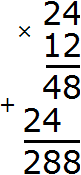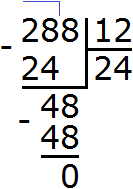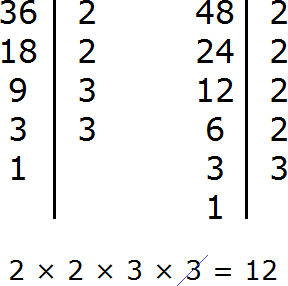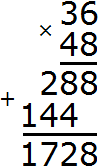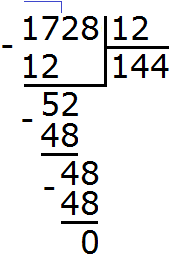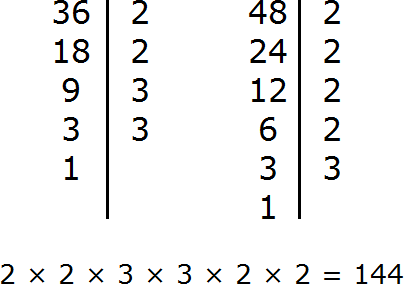Как находят нод и нок

НОД и НОК

Продолжаем изучать деление. В данном уроке мы рассмотрим такие понятия, как НОД и НОК.

НОД — это наибольший общий делитель.

НОК — это наименьшее общее кратное.

Тема довольно скучная, но разобраться в ней нужно обязательно. Не понимая этой темы, не получится эффективно работать с дробями, которые являются настоящей преградой в математике.

Наибольший общий делитель

Определение. Наибольшим общим делителем чисел a и b называется наибольшее число, на которое a и b делятся без остатка.

Чтобы хорошо понять это определение, подставим вместо переменных a и b любые два числа. Например, вместо переменной a подставим число 12, а вместо переменной b — число 9. Теперь попробуем прочитать это определение:

Наибольшим общим делителем чисел 12 и 9 называется наибольшее число, на которое 12 и 9 делятся без остатка.

Из определения понятно, что речь идёт об общем делителе чисел 12 и 9. Причем делитель является наибольшим из всех существующих делителей. Этот наибольший общий делитель (НОД) нужно найти.

Для нахождения наибольшего общего делителя двух чисел, используется три способа. Первый способ довольно трудоёмкий, но зато позволяет хорошо понять суть темы и прочувствовать весь ее смысл.

Второй и третий способы довольны просты и дают возможность быстро найти НОД. Рассмотрим все три способа. А какой применять на практике — выбирать вам.

Первый способ заключается в поиске всех возможных делителей двух чисел и в выборе наибольшего из них. Рассмотрим этот способ на следующем примере: найти наибольший общий делитель чисел 12 и 9.

Сначала найдём все возможные делители числа 12. Для этого разделим 12 на все делители в диапазоне от 1 до 12. Если делитель позволит разделить 12 без остатка, то мы будем выделять его синим цветом и в скобках делать соответствующее пояснение.

12 : 1 = 12
(12 разделилось на 1 без остатка, значит 1 является делителем числа 12)

12 : 2 = 6
(12 разделилось на 2 без остатка, значит 2 является делителем числа 12)

12 : 3 = 4
(12 разделилось на 3 без остатка, значит 3 является делителем числа 12)

12 : 4 = 3
(12 разделилось на 4 без остатка, значит 4 является делителем числа 12)

12 : 5 = 2 (2 в остатке)
(12 не разделилось на 5 без остатка, значит 5 не является делителем числа 12)

12 : 6 = 2
(12 разделилось на 6 без остатка, значит 6 является делителем числа 12)

12 : 7 = 1 (5 в остатке)
(12 не разделилось на 7 без остатка, значит 7 не является делителем числа 12)

12 : 8 = 1 (4 в остатке)
(12 не разделилось на 8 без остатка, значит 8 не является делителем числа 12)

12 : 9 = 1 (3 в остатке)
(12 не разделилось на 9 без остатка, значит 9 не является делителем числа 12)

12 : 10 = 1 (2 в остатке)
(12 не разделилось на 10 без остатка, значит 10 не является делителем числа 12)

12 : 11 = 1 (1 в остатке)
(12 не разделилось на 11 без остатка, значит 11 не является делителем числа 12)

12 : 12 = 1
(12 разделилось на 12 без остатка, значит 12 является делителем числа 12)

Теперь найдём делители числа 9. Для этого проверим все делители от 1 до 9

9 : 1 = 9
(9 разделилось на 1 без остатка, значит 1 является делителем числа 9)

9 : 2 = 4 (1 в остатке)
(9 не разделилось на 2 без остатка, значит 2 не является делителем числа 9)

9 : 3 = 3
(9 разделилось на 3 без остатка, значит 3 является делителем числа 9)

9 : 4 = 2 (1 в остатке)
(9 не разделилось на 4 без остатка, значит 4 не является делителем числа 9)

9 : 5 = 1 (4 в остатке)
(9 не разделилось на 5 без остатка, значит 5 не является делителем числа 9)

9 : 6 = 1 (3 в остатке)
(9 не разделилось на 6 без остатка, значит 6 не является делителем числа 9)

9 : 7 = 1 (2 в остатке)
(9 не разделилось на 7 без остатка, значит 7 не является делителем числа 9)

9 : 8 = 1 (1 в остатке)
(9 не разделилось на 8 без остатка, значит 8 не является делителем числа 9)

9 : 9 = 1
(9 разделилось на 9 без остатка, значит 9 является делителем числа 9)

Теперь выпишем делители обоих чисел. Числа выделенные синим цветом и являются делителями. Их и выпишем:

Выписав делители, можно сразу определить какой является наибольшим и общим.

Согласно определению, наибольшим общим делителем чисел 12 и 9, является число, на которое 12 и 9 делятся без остатка. Наибольшим и общим делителем чисел 12 и 9 является число 3

И число 12 и число 9 делятся на 3 без остатка:

Значит НОД (12 и 9) = 3

Второй способ нахождения НОД

Теперь рассмотрим второй способ нахождения наибольшего общего делителя. Суть данного способа заключается в том, чтобы разложить оба числа на простые множители и перемножить общие из них.

Пример 1. Найти НОД чисел 24 и 18

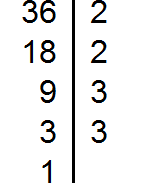
Сначала разложим оба числа на простые множители:

Теперь перемножим их общие множители. Чтобы не запутаться, общие множители можно подчеркнуть.

Смотрим на разложение числа 24. Первый его множитель это 2. Ищем такой же множитель в разложении числа 18 и видим, что он там тоже есть. Подчеркиваем обе двойки:

Снова смотрим на разложение числа 24. Второй его множитель тоже 2. Ищем такой же множитель в разложении числа 18 и видим, что его там второй раз уже нет. Тогда ничего не подчёркиваем.

Следующая двойка в разложении числа 24 также отсутствует в разложении числа 18.

Переходим к последнему множителю в разложении числа 24. Это множитель 3. Ищем такой же множитель в разложении числа 18 и видим, что там он тоже есть. Подчеркиваем обе тройки:

Итак, общими множителями чисел 24 и 18 являются множители 2 и 3. Чтобы получить НОД, эти множители необходимо перемножить:

Значит НОД (24 и 18) = 6

Третий способ нахождения НОД

Теперь рассмотрим третий способ нахождения наибольшего общего делителя. Суть данного способа заключается в том, что числа подлежащие поиску наибольшего общего делителя раскладывают на простые множители. Затем из разложения первого числа вычеркивают множители, которые не входят в разложение второго числа. Оставшиеся числа в первом разложении перемножают и получают НОД.

Пример 1. Найти НОД чисел 28 и 16.

В первую очередь, раскладываем числа 28 и 16 на простые множители:

Получили два разложения: 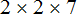и

Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входит семёрка. Её и вычеркнем из первого разложения:

Теперь перемножаем оставшиеся множители и получаем НОД:

Число 4 является наибольшим общим делителем чисел 28 и 16. Оба этих числа делятся на 4 без остатка:

Пример 2. Найти НОД чисел 100 и 40

Раскладываем на множители число 100

Раскладываем на множители число 40

Получили два разложения: 2 × 2 × 5 × 5 и 2 × 2 × 2 × 5

Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входит одна пятерка (там только одна пятёрка). Её и вычеркнем из первого разложения

Перемножим оставшиеся числа:

Получили ответ 20. Значит число 20 является наибольшим общим делителем чисел 100 и 40. Эти два числа делятся на 20 без остатка:

Пример 3. Найти НОД чисел 72 и 128

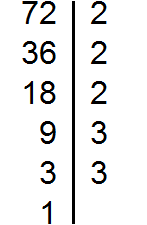
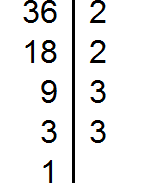
Раскладываем на множители число 72

Раскладываем на множители число 128

Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входят две тройки (там их вообще нет). Их и вычеркнем из первого разложения:

Перемножим оставшиеся числа:

Получили ответ 8. Значит число 8 является наибольшим общим делителем чисел 72 и 128. Эти два числа делятся на 8 без остатка:

Нахождение НОД для нескольких чисел

Наибольший общий делитель можно находить и для нескольких чисел, а не только для двух. Для этого числа, подлежащие поиску наибольшего общего делителя, раскладывают на простые множители, затем находят произведение общих простых множителей этих чисел.

Например, найдём НОД для чисел 18, 24 и 36

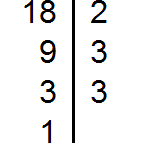
Разложим на множители число 18

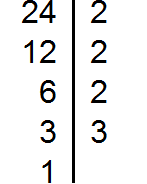
Разложим на множители число 24

Разложим на множители число 36

Получили три разложения:

Теперь найдём и подчеркнём общие множители:

Мы видим, что общие множители для чисел 18, 24 и 36 это множители 2 и 3. Эти множители входят во все три разложения. Перемножив эти множители, мы получим НОД, который ищем:

Получили ответ 6. Значит число 6 является наибольшим общим делителем чисел 18, 24 и 36. Эти три числа делятся на 6 без остатка:

Пример 2. Найти НОД для чисел 12, 24, 36 и 42

Разложим на простые множители каждое число. Затем найдём произведение общих простых множителей.

Разложим на множители число 12

Разложим на множители число 24

Разложим на множители число 36

Разложим на множители число 42

Получили четыре разложения:

Теперь найдём и подчеркнём общие множители:

Мы видим, что общие множители для чисел 12, 24, 36, и 42 это множители 2 и 3. Перемножив эти множители, мы получим НОД, который ищем:

Получили ответ 6. Значит число 6 является наибольшим общим делителем чисел 12, 24, 36 и 42. Эти числа делятся на 6 без остатка:

Наименьшее общее кратное

Из предыдущего урока мы знаем, что если какое-то число без остатка разделилось на другое, его называют кратным этого числа.

Оказывается, кратное может быть общим у нескольких чисел. И сейчас нас будет интересовать кратное двух чисел, причем оно должно быть максимально маленьким.

Определение. Наименьшее общее кратное (НОК) чисел a и b — это наименьшее число, которое кратно a и b. Другими словами, это такое маленькое число, которое делится без остатка на число a и число b.

Определение содержит две переменные a и b. Давайте подставим вместо этих переменных любые два числа. Например, вместо переменной a подставим число 9, а вместо переменной b подставим число 12. Теперь попробуем прочитать определение:

Наименьшее общее кратное (НОК) чисел 9 и 12 — это наименьшее число, которое кратно 9 и 12. Другими словами, это такое маленькое число, которое делится без остатка на число 9 и на число 12.

Из определения понятно, что наименьшее общее кратное это наименьшее число, которое делится без остатка на 9 и на 12. Это наименьшее общее кратное требуется найти.

Для нахождения наименьшего общего кратного (НОК) можно пользоваться тремя способами. Первый способ заключается в том, что можно выписать первые кратные двух чисел, а затем выбрать среди этих кратных такое число, которое будет общим для обоих чисел и маленьким. Давайте применим этот способ.

В первую очередь, найдем первые кратные для числа 9. Чтобы найти кратные для 9, нужно эту девятку поочерёдно умножить на числа от 1 до 9. Получаемые ответы будут кратными для числа 9.

Итак, начнём. Кратные будем выделять синим цветом:

Теперь находим кратные для числа 12. Для этого поочерёдно умножим число 12 на все числа 1 до 12:

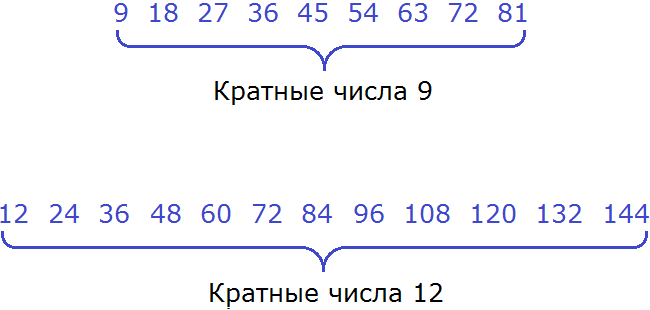
Теперь выпишем кратные обоих чисел:

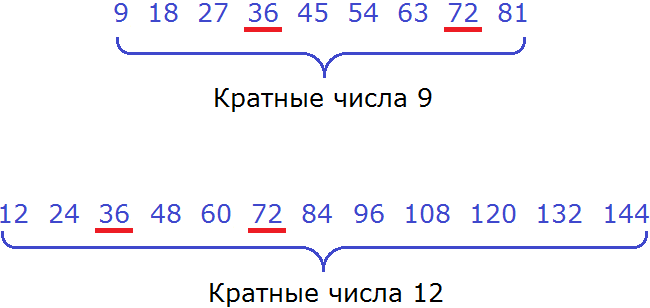
Теперь найдём общие кратные обоих чисел. Найдя, сразу подчеркнём их:

Общими кратными для чисел 9 и 12 являются кратные 36 и 72. Наименьшим же из них является 36.

Значит наименьшее общее кратное для чисел 9 и 12 это число 36. Данное число делится на 9 и 12 без остатка:

Второй способ нахождения НОК

Второй способ заключается в том, что числа для которых ищется наименьшее общее кратное раскладываются на простые множители. Затем выписываются множители, входящие в первое разложение, и добавляют недостающие множители из второго разложения. Полученные множители перемножают и получают НОК.

Применим данный способ для предыдущей задачи. Найдём НОК для чисел 9 и 12.

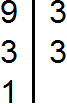
Разложим на множители число 9

Разложим на множители число 12

Выпишем первое разложение:

Теперь допишем множители из второго разложения, которых нет в первом разложении. В первом разложении нет двух двоек. Их и допишем:

Теперь перемножаем эти множители:

Получили ответ 36. Значит наименьшее общее кратное чисел 9 и 12 это число 36. Данное число делится на 9 и 12 без остатка:

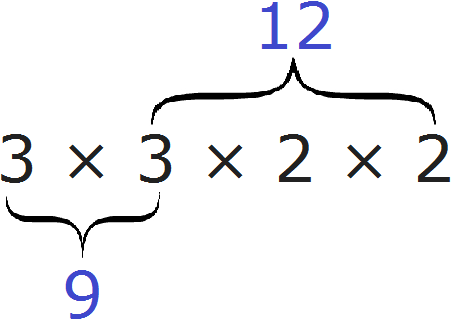
Говоря простым языком, всё сводится к тому, чтобы организовать новое разложение куда входят оба разложения сразу. Разложением первого числа 9 являлись множители 3 и 3, а разложением второго числа 12 являлись множители 2, 2 и 3.

Пример 2. Найти НОК чисел 50 и 180

Разложим на множители число 50

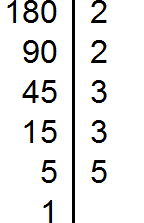
Разложим на множители число 180

Выпишем первое разложение:

Теперь допишем множители из второго разложения, которых нет первом разложении. В первом разложении нет ещё одной двойки и двух троек. Их и допишем:

Теперь перемножаем эти множители:

Получили ответ 900. Значит наименьшее общее кратное чисел 50 и 180 это число 900. Данное число делится на 50 и 180 без остатка:

Пример 3. Найти НОК чисел 8, 15 и 33

Разложим на множители число 8

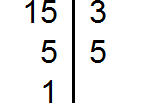
Разложим на множители число 15

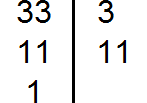
Разложим на множители число 33

Выпишем первое разложение:

Теперь допишем множители из второго и третьего разложения, которых нет первом разложении. Допишем множители 3 и 5 из второго разложения, и множитель 11 из третьего разложения:

Теперь перемножаем эти множители:

Получили ответ 1320. Значит наименьшее общее кратное чисел 8, 15 и 33 это число 1320. Данное число делится на 8, 15 и 33 без остатка:

НОК (8, 15 и 33) = 1320

Третий способ нахождения НОК

Есть и третий способ нахождения наименьшего общего кратного. Он работает при условии, что его ищут для двух чисел и при условии, что уже найден наибольший общий делитель этих чисел.

Данный способ разумнее использовать, когда одновременно нужно найти НОД и НОК двух чисел.

К примеру, пусть требуется найти НОД и НОК чисел 24 и 12. Сначала найдем НОД этих чисел:

Теперь для нахождения наименьшего общего кратного чисел 24 и 12, нужно перемножить эти два числа и полученный результат разделить на их наибольший общий делитель.

Итак, перемножим числа 24 и 12

Разделим полученное число 288 на НОД чисел 24 и 12

Получили ответ 24. Значит наименьшее общее кратное чисел 24 и 12 равно 24

Пример 2. Найти НОД и НОК чисел 36 и 48

Найдем НОД чисел 36 и 48

Перемножим числа 36 и 48

Разделим 1728 на НОД чисел 36 и 48

Получили 144. Значит наименьшее общее кратное чисел 36 и 48 равно 144

Для проверки можно найти НОК обычным вторым способом, которым мы пользовались ранее. Если мы всё сделали правильно, то должны получить 144

Не расстраивайтесь, если сразу не научитесь находить НОД и НОК. Главное понимать, что это такое и как оно работает. А ошибки вполне естественны на первых порах. Как говорят: «На ошибках учимся».

Источник

Нахождение наименьшего общего кратного: способы, примеры нахождения НОК

Продолжим разговор о наименьшем общем кратном, который мы начали в разделе « НОК – наименьшее общее кратное, определение, примеры». В этой теме мы рассмотрим способы нахождения НОК для трех чисел и более, разберем вопрос о том, как найти НОК отрицательного числа.

Вычисление наименьшего общего кратного (НОК) через НОД

Мы уже установили связь наименьшего общего кратного с наибольшим общим делителем. Теперь научимся определять НОК через НОД. Сначала разберемся, как делать это для положительных чисел.

Решение

Решение

В этом примере мы использовали правило нахождения наименьшего общего кратного для целых положительных чисел a и b : если первое число делится на второе, что НОК этих чисел будет равно первому числу.

Нахождение НОК с помощью разложения чисел на простые множители

Теперь давайте рассмотрим способ нахождения НОК, который основан на разложении чисел на простые множители.

Для нахождения наименьшего общего кратного нам понадобится выполнить ряд несложных действий:

Решение

Найдем все простые множители чисел, данных в условии:

441 147 49 7 1 3 3 7 7

700 350 175 35 7 1 2 2 5 5 7

Дадим еще одну формулировку метода нахождения НОК путем разложения чисел на простые множители.

Раньше мы исключали из всего количества множителей общие для обоих чисел. Теперь мы сделаем иначе:

Решение

Нахождение НОК трех и большего количества чисел

Независимо от того, с каким количеством чисел мы имеем дело, алгоритм наших действий всегда будет одинаковым: мы будем последовательно находить НОК двух чисел. На этот случай есть теорема.

Теперь рассмотрим, как можно применять теорему для решения конкретных задач.

Решение

Как видите, вычисления получаются несложными, но достаточно трудоемкими. Чтобы сэкономить время, можно пойти другим путем.

Предлагаем вам следующий алгоритм действий:

Решение

Нахождение наименьшего общего кратного отрицательных чисел

Для того, чтобы найти наименьшее общее кратное отрицательных чисел, эти числа необходимо сначала заменить на числа с противоположным знаком, а затем провести вычисления по приведенным выше алгоритмам.

Решение

Источник

Целые числа (натуральные и отрицательные числа, НОК и НОД)

Чтобы намного упростить себе жизнь когда надо что-то вычислить, чтобы выиграть драгоценное время на ОГЭ или ЕГЭ, чтобы сделать меньше глупых ошибок, – читай эту статью!

Вот чему ты научишься:

Целые числа — коротко о главном

Множество целых чисел состоит из 3 частей:

Множество целых чисел обозначается буквой Z.

Натуральные числа

Натуральные числа – это числа, которые мы употребляем для счета предметов.

Множество натуральных чисел обозначается буквой N.

В операциях с целыми числами понадобится умение находить НОД и НОК.

Наибольший общий делитель (НОД)

Чтобы найти НОД, необходимо:

Наименьшее общее кратное (НОК)

Чтобы найти НОК, необходимо:

Отрицательные числа

Числа, противоположные натуральным, то есть:

Ноль

Не дели на ноль! 🙂

Натуральные числа

Множество целых чисел состоит из 3 частей:

Множество целых чисел обозначается буквой Z.

«Бог создал натуральные числа, всё остальное – дело рук человеческих» (c) Немецкий математик Кронекер.

Натуральные числа – это числа, которые мы употребляем для счета предметов, и именно на этом основывается их история возникновения – необходимости считать стрелы, шкуры и т.д.

1, 2, 3, 4… n

Множество натуральных чисел обозначается буквой N.

Кроме этого, не входят и все дробные числа (мы также не можем сказать « у меня есть 1,5 ноутбука», или «я продал 2,5 машины»)

Любое натуральное число можно записать с помощью 10 цифр:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9

Таким образом, 14 – это не цифра. Это число. Из каких цифр оно состоит? Правильно, из цифр 1 и 4.

Натуральные числа можно складывать, вычитать, умножать и делить.

Сложение. Группировка при сложении чисел

Что интересного ты можешь сказать про эту процедуру?

Конечно, ты сейчас ответишь «от перестановки слагаемых значение суммы не меняется».

Казалось бы, примитивное, знакомое с первого класса правило, однако, при решении больших примеров оно моментально забывается!

Не забывай про него — используй группировку, чтобы облегчить себе процесс подсчета и снизить вероятность ошибок, ведь на ЕГЭ калькулятора у тебя не будет.

Смотри сам, какое выражение легче сложить?

Конечно же второе! Хотя результат один и тот же. Но! считая вторым способом у тебя меньше шансов ошибиться и ты все сделаешь быстрее!

Итак, ты в уме считаешь вот так:

4 + 5 + 3 + 6 = 4 + 6 + 5 + 3 = 10 + 5 + 3 = 18

Вычитание. Группировка при вычитании чисел

При вычитании мы также можем группировать вычитаемые числа, например:

32 — 5 — 2 — 6 = (32 — 2) — 5 — 6 = 30 — 5 — 6 = 19

А что, если вычитание чередуется в примере со сложением? Так же можно группировать, ответишь ты, и это правильно. Только прошу, не забывай о знаках перед числами, например: 32 — 5 — 2 — 6 = (32 — 2) — (6 + 5) = 30 — 11 = 19

Помни: неправильно проставленные знаки приведут к ошибочному результату.

Очевидно, что от перемены мест множителей значение произведения также не изменится:

Я не буду говорить тебе «используй это при решении примеров» (ты и сам понял намек, правда?), а лучше расскажу, как быстро умножать некоторые числа в уме.

Умножение. Как быстро умножать в уме

Итак, внимательно смотри таблицу:

И еще немного об умножении. Конечно, ты помнишь два особых случая…

Догадываешься, о чем я?

Ну что здесь можно сказать интересного?

Число может делиться на другое нацело (то есть, без остатка) и с остатком, который всегда меньше делителя, что вполне логично.

Особые случаи, если при делении у нас есть 0.

Чему будет равен пример, если 0 является делителем и чему равен пример, если он делимое?

Ах да, еще рассмотрим признаки делимости.

Всего существует 7 правил по признакам делимости, из которых первые 3 ты точно уже знаешь!

А вот остальные совсем не сложно запомнить.

Признаки делимости чисел

Первые три правила ты, конечно же, знаешь.

Четвертое и пятое легко запомнить – при делении на 3 и 9 мы смотрим, делится ли на это сумма цифр, составляющих число.

При делении на 4 мы обращаем внимание на две последние цифры числа — делится ли число, которое они составляют на 4?

При делении на 6 число должно одновременно делиться на 2 и на 3. Вот и вся премудрость.

Ты сейчас думаешь: «зачем мне все это»?

Во-первых, ЕГЭ проходит без калькулятора и данные правила помогут тебе сориентироваться в примерах.

А во-вторых, ты же слышал задачи про НОД и НОК? Знакомая аббревиатура? Начнем вспоминать и разбираться.

Наибольший общий делитель (НОД)

Наибольший общий делитель (НОД) — нужен для сокращения дробей и быстрых вычислений.

Допустим, у тебя есть два числа: 12 и 8.

На какое наибольшее число делятся оба этих числа? Ты, не задумываясь, ответишь 4, потому что знаешь, что:

Какие цифры в разложении общие?

Правильно, 2 * 2 = 4. Вот и твой ответ был 4.

Держа в голове этот простой пример, ты не забудешь алгоритм, как находить НОД.

Попробуй «выстроить» его у себя в голове. Получилось?

Чтобы найти НОД необходимо:

Понимаешь, зачем нам нужны были признаки делимости? Чтобы ты посмотрел на число и мог начать делить без остатка.

Найдем НОД числа 290

Глядя на него, ты сразу можешь сказать, что оно делится на 10, запишем:

29 больше разделить ни на что нельзя, а вот 10 можно – 5 и 2, получаем:

Найдем НОД числа 485.

По признакам делимости оно должно без остатка делиться на 5, так как на 5 заканчивается. Делим:

Проанализируем изначальное число.

На 2 оно делиться не может (последняя цифра – нечетная),
85 – не делится на 4, значит число тоже не делится на 4,

На 3 и на 9 также не делится (сумма цифр, входящих в число, не делится на 3 и на 9)

На 6 тоже не делится, так как не делится на 2 и 3,

На 8 тоже не делится, так как не делится на 2 и 4.

97 нельзя разделить на 7 нацело,

Значит, число 485 можно разложить только на 5 и 97.

А теперь найдем НОД этих чисел (290 и 485).

Совет: глядя на числа можно иногда сразу найти хотя бы один общий делитель. Раздели сначала на него, а потом уже раскладывай дальше. При этом, необязательно общий делитель раскладывать на его составляющие – все равно потом ты будешь их снова перемножать.

Задача №1. Найти НОД чисел 6240 и 6800

1) Делю сразу на 10, так как оба числа 100% делятся на 10:

2) Разделю на 4 оставшиеся большие числа (624 и 680), так как 24 и 80 без остатка делятся на 4 (при этом, 10раскладывать не буду – он и так общий делитель):

3) Оставлю 4 и 10 в покое и начну рассматривать числа 156 и 170. Оба числа точно делятся на 2 (заканчиваются на четные цифры (0 в таком случае представляем как 10, а 10 можно разделить на 2)):

4) Работаем с числами 78 и 85. Есть ли у них общие делители? Так легко, как в предыдущих действиях, и не скажешь, поэтому дальше просто разложим их на простые множители:

5) Как мы видим, мы были правы: у 78 и 85 общих делителей нет, и теперь нам нужно перемножить 10⋅4⋅2=80.

НОД (6240; 6800)=80

Задача №2. Найти НОД чисел 345 и 324

Здесь не могу быстро найти хоть один общий делитель, так что просто раскладываю на простые множители (как можно меньше):

Точно, НОД (345; 324)=3, а я изначально не проверила признак делимости на 3, и, возможно, не пришлось бы делать столько действий.

Но ты-то проверил, верно?

Как видишь, это совсем несложно.

Наименьшее общее кратное (НОК) — экономит время, помогает решить задачи нестандартно

Допустим, у тебя есть два числа – 8 и 16. Какое существует самое маленькое число, которое делится 8 и 16 без остатка(то есть нацело)? Сложно представить? Вот тебе визуальная подсказка:

Ты же помнишь, что обозначается буквой ℤ? Правильно, как раз целые числа. Так какое наименьшее число подходит на место х? 𝑥=16:

В данном случае НОК(8;16)=16.

Из этого простого примера вытекает несколько правил.

Наименьшее общее кратное (НОК)

Правила быстрого нахождения НОК.

Правило 1

Если одно из двух натуральных чисел делится на другое число, то большее из этих двух чисел является их наименьшим общим кратным.

Найди НОК у следующих чисел:

Конечно, ты без труда справился с этой задачей и у тебя получились ответы – 21,12, 15 и 33.

Заметь, в правиле мы говорим о ДВУХ числах, если чисел будет больше, то правило не работает.

Например, НОК (7;14;21) не равно 21, так как 21не делится без остатка на 14.

Правило 2

Если два (или более двух) числа являются взаимно простыми, то наименьшее общее кратное равно их произведению.

Найди НОК у следующих чисел:

Посчитал? Вот ответы – 21, 231, 42; 30.

Как ты понимаешь, не всегда можно так легко взять и подобрать этот самый х, поэтому для чуть более сложных чисел существует следующий алгоритм:

Найдем наименьшее общее кратное – НОК (345; 234)

Раскладываем каждое число:

Почему я сразу написал 3⋅2?

Вспомни признаки делимости на 6: делится на 2 (последняя цифра – четная) и сумма цифр делится на 3 (2+3+4=9).

Соответственно, можем сразу разделить 234 на 6, записав ее как 3⋅2.

Теперь выписываем в строчку наиболее длинное разложение – второе:

Добавим к нему числа из первого разложения, которых нет в том, что мы выписали:

Заметь: мы выписали все кроме 3, так как она у нас уже есть.

Теперь нам необходимо все эти числа перемножить!

НОК(345;234)=26910

Найди наименьшее общее кратное (НОК) (6240;6800) и (345;324)

Какие ответы у тебя получились?

Вот, что вышло у меня:

Сколько времени ты потратил на нахождение НОК? Мое время – 2 минуты, правда я знаю одну хитрость, которую предлагаю тебе открыть прямо сейчас!

Если ты очень внимателен, то ты наверное заметил, что по заданным числам мы уже искали НОД и разложение на множители этих чисел ты мог взять из того примера, тем самым упростив себе задачу, но это далеко не все.

Посмотри на картинку, возможно, к тебе придут еще какие-нибудь мысли:

Ну что? Сделаю подсказку: попробуй перемножить НОК и НОД между собой и запиши все множители, которые будут при перемножении. Справился? У тебя должна получиться вот такая цепочка:

Присмотрись к ней повнимательней: сравни множители с тем, как раскладываются 6240 и 6800.

Какой вывод ты можешь сделать из этого? Правильно! Если мы перемножим значения НОК и НОД между собой, то мы получим произведение этих чисел.

Соответственно, имея числа и значение НОД (или НОК), мы можем найти НОК (или НОД) по такой схеме:

1. Находим произведение чисел:

2. Делим получившееся произведение на наш НОД (6240; 6800) = 80:

Запишем правило в общем виде:

Попробуй найти НОД, если известно, что:

Справился? НОД(345; 234)=3.

Отрицательные числа – «лжечисла» и их признание человечеством

Как ты уже понял, это числа, противоположные натуральным, то есть:

Отрицательные числа можно складывать, вычитать, умножать и делить – все как в натуральных.

Казалось бы, что в них такого особенного?

А дело в том, что отрицательные числа «отвоевывали» себе законное место в математике аж до XIX века (до этого момента было огромное количество споров, существуют они или нет).

Само отрицательное число возникло из-за такой операции с натуральными числами, как «вычитание».

Действительно, из 3 вычесть 11 – вот и получается отрицательное число. Именно поэтому, множество отрицательных чисел часто называют «расширением множества натуральных чисел».

Отрицательные числа долго не признавались людьми.

Так, Древний Египет, Вавилон и Древняя Греция – светочи своего времени, не признавали отрицательных чисел, а в случае получения отрицательных корней в уравнении (например, как у нас 3−11), корни отвергались как невозможные.

Впервые отрицательные числа получили свое право на существование в Китае, а затем в VII веке в Индии.

Как ты думаешь, с чем связано это признание?

Правильно, отрицательными числами стали обозначать долги (иначе — недостачу).

Считалось, что отрицательные числа – это временное значение, которое в результате изменится на положительное (то есть, деньги кредитору все же вернут). Однако, индийский математик Брахмагупта уже тогда рассматривал отрицательные числа наравне с положительными.

В Европе к полезности отрицательных чисел, а также к тому, что они могут обозначать долги, пришли значительно позже, эдак, на тысячелетие.

Первое упоминание замечено в 1202 году в «Книге абака» Леонарда Пизанского (сразу говорю — к Пизанской башне автор книги отношения никакого не имеет, а вот числа Фибоначчи – это его рук дело (прозвище Леонардо Пизанского — Фибоначчи)).

Далее европейцы пришли к тому, что отрицательные числа могут обозначать не только долги, но и нехватку чего бы то ни было, правда, признавали это не все.

Так, в XVII веке Паскаль считал что 0−4=0.

Как думаешь, чем он это обосновывал?

Верно, «ничто не может быть меньше НИЧЕГО».

Отголоском тех времен остается тот факт, что отрицательное число и операция вычитания обозначается одним и тем же символом – минусом «-». И правда: 6−8. Число «8» положительное, которое вычитается из 6, или отрицательное, которое суммируется к 6?… Что-то из серии «что первое: курица или яйцо?» Вот такая вот, своеобразная эта математическая философия.

Отрицательные числа закрепили свое право на существование с появлением аналитической геометрии, иначе говоря, когда математики ввели такое понятие как числовая ось.

Именно с этого момента наступило равноправие. Однако все равно вопросов было больше чем ответов, например:

пропорция \( \displaystyle \frac<1><-1>=\frac<-1><1>\)

Данная пропорция носит название «парадокс Арно». Подумай, что в ней сомнительного?

В итоге, математики договорились до того, что Карл Гаусс (да, да, это тот самый, который считал сумму \( \displaystyle 40\) (или \( \displaystyle 100\)) чисел) в 1831 году поставил точку.

Он сказал, что отрицательные числа имеют те же права, что и положительные, а то, что они применимы не ко всем вещам, ничего не означает, так как дроби так же не применимы ко многим вещам (не бывает так, что яму роют \( \displaystyle 1,5\) землекопа, нельзя купить \( \displaystyle 4,5\) билета в кино и т.д.).

Успокоились математики только в XIX веке, когда Уильямом Гамильтоном и Германом Грассманом была создана теория отрицательных чисел.

Вот такие они спорные, эти отрицательные числа.

Возникновение «пустоты» или биография нуля

В математике \( \displaystyle 0\) – особенное число.

С первого взгляда, это ничто: прибавить \( \displaystyle 0\), отнять \( \displaystyle 0\) – ничего не изменится, но стоит только приписать его справа к «\( \displaystyle 1\)», и полученное число \( \displaystyle 10\) будет в \( \displaystyle 10\) раз больше изначального.

Умножением на ноль мы все превращаем в ничто, а разделить на «ничто», то есть \( \displaystyle 0\), мы не можем. Одним словом, волшебное число)

История нуля длинная и запутанная.

След нуля найден в сочинениях китайцев во 2 тыс. н.э. и ещё раньше у майя. Первое использование символа нуля, каковым он является в наши дни, было замечено у греческих астрономов.

Существует множество версий, почему было выбрано именно такое обозначение «ничего».

Некоторые историки склоняются к тому, что это омикрон, т.е. первая буква греческого слова ничто – ouden. Согласно другой версии, жизнь символу ноля дало слово «обол» (монета, почти не имеющая ценности).

Ноль (или нуль) как математический символ впервые появляется у индийцев (заметь, там же стали «развиваться» отрицательные числа).

Первые достоверные свидетельства о записи нуля относятся к 876 г., и в них «\( \displaystyle 0\)» – составляющая числа \( \displaystyle 270\).

В Европу ноль также пришел с запозданием — лишь в 1600г., и также как и отрицательные числа, сталкивался с сопротивлением (что поделаешь, такие они, европейцы).

«Нуль часто ненавидели, издавна боялись, а то и запрещали» — пишет американский математик Чарльз Сейф.

Так, турецкий султан Абдул-Хамид II в конце XIXв. приказал своим цензорам вычеркнуть из всех учебников химии формулу воды H2O, принимая букву «О» за нуль и не желая, чтобы его инициалы порочились соседством с презренным нулём».

На просторах интернета можно встретить фразу: «Ноль — самая могущественная сила во Вселенной, он может всё! Ноль создаёт порядок в математике, и он же вносит в неё хаос». Абсолютно верно подмечено:)

Источник