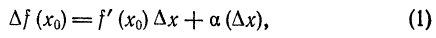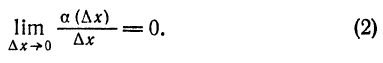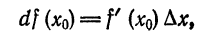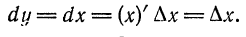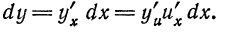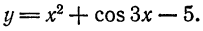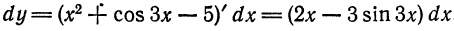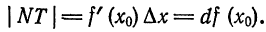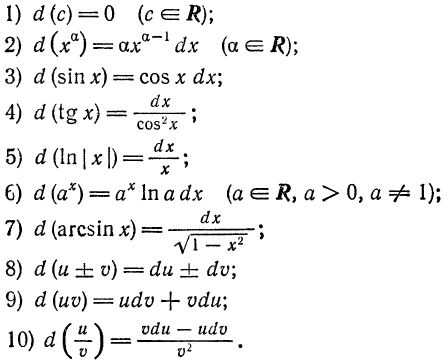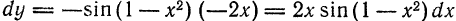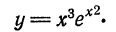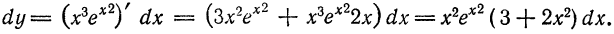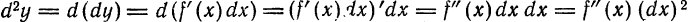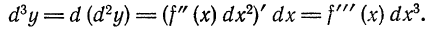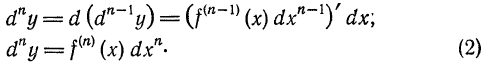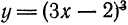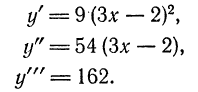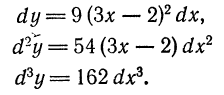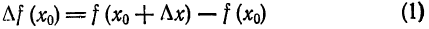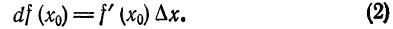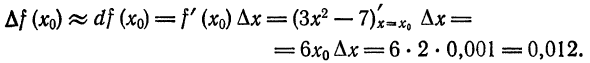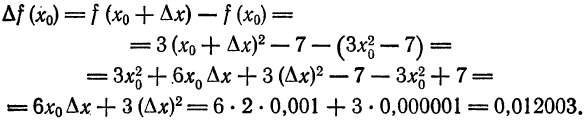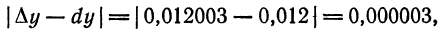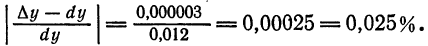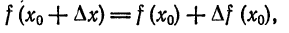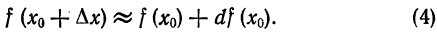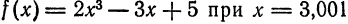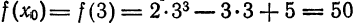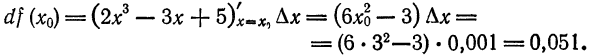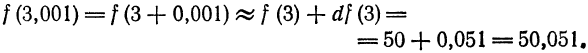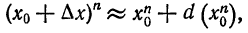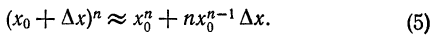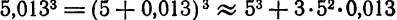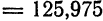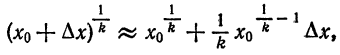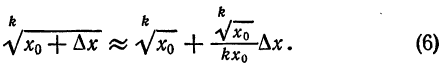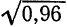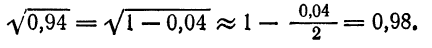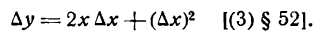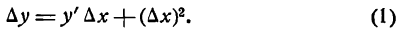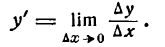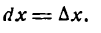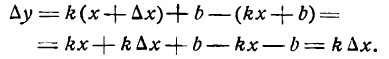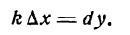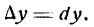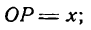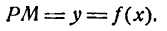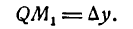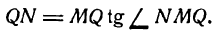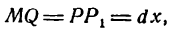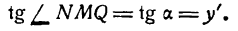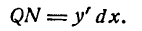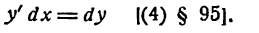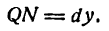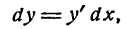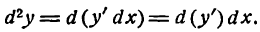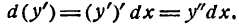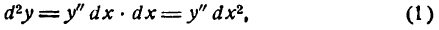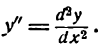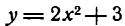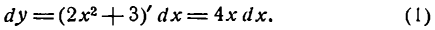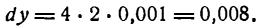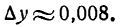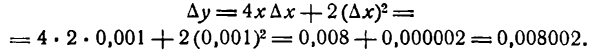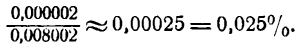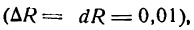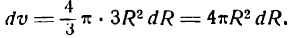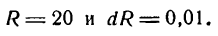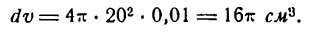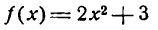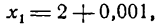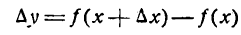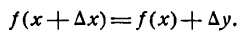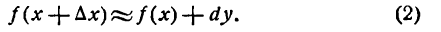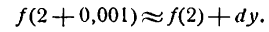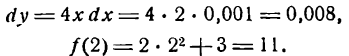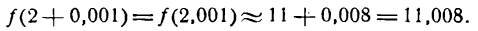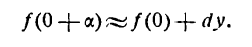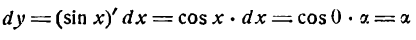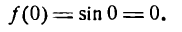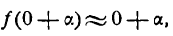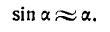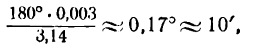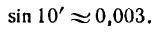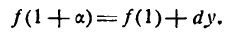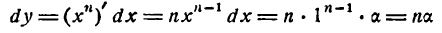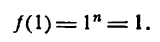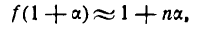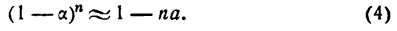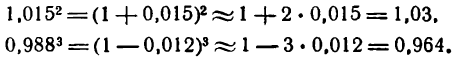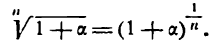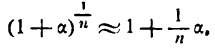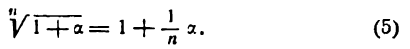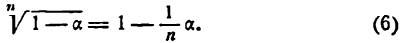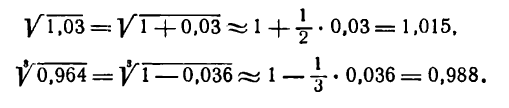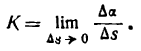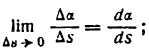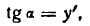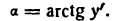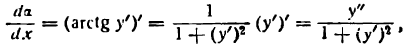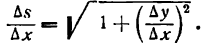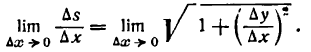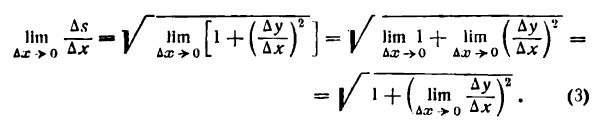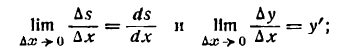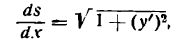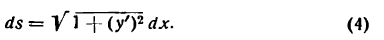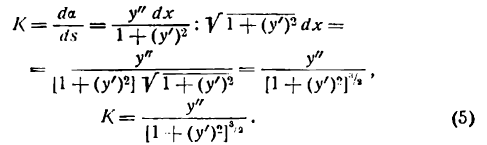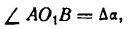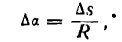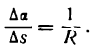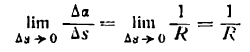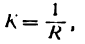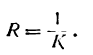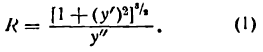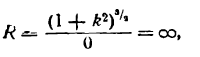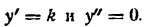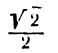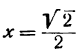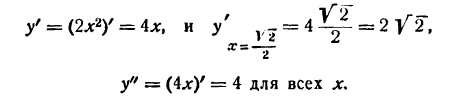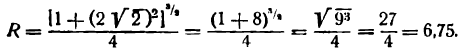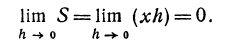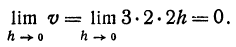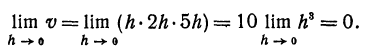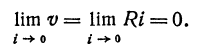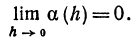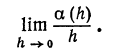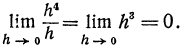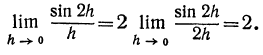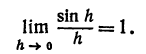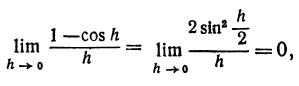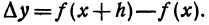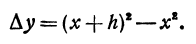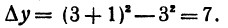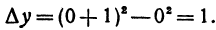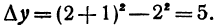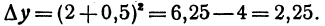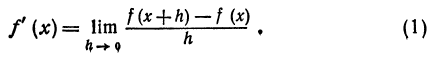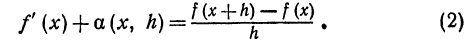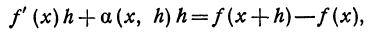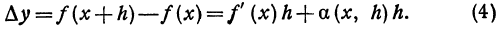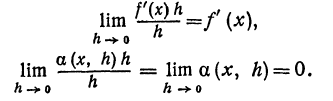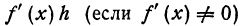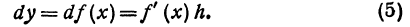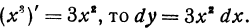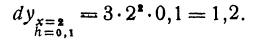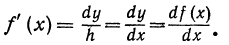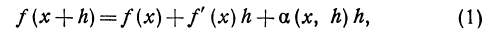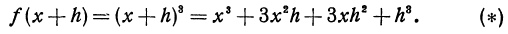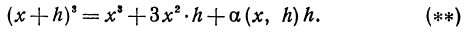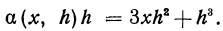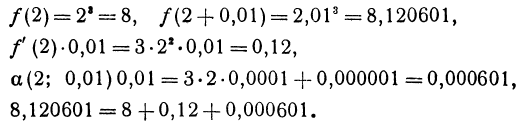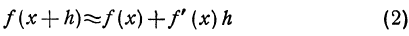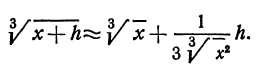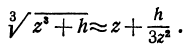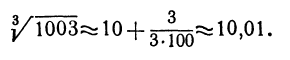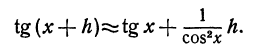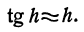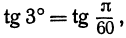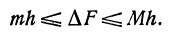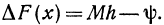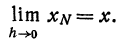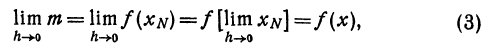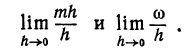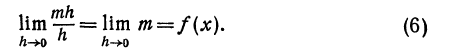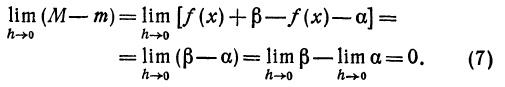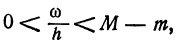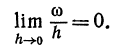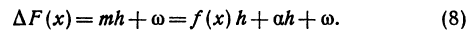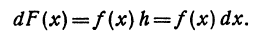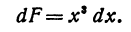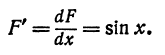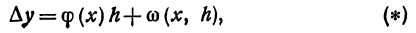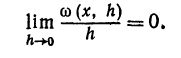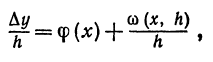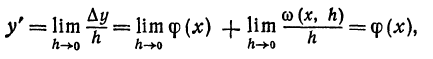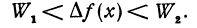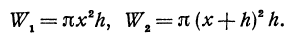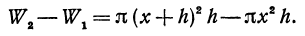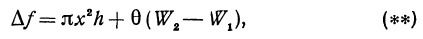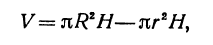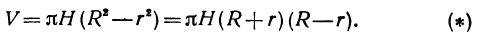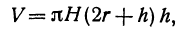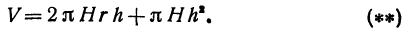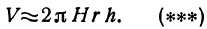Как находятся дифференциалы высших порядков
Будь умным!
Работа добавлена на сайт samzan.ru: 2016-03-13
Производные и дифференциалы высших порядков, их свойства. Точки экстремума функции. Теоремы Ферма и Ролля.
Свойства производных высших порядков.
Основные свойства производных высших порядков следуют из соответствующих свойств первой производной:
Заметим, что коэффициенты в этой формуле совпадают с соответствующими коэффициентами формулы бинома Ньютона, если заменить производные данного порядка той же степенью переменной. Для n =1 эта формула была получена при изучении первой производной, для производных высших порядков ее справедливость можно доказать с помощью метода математической индукции.
Дифференциалы высших порядков.
Обозначение: d ² y = d ( dy ).
При вычислении второго дифференциала учтем, что dx не зависит от х и при дифференцировании выносится за знак производной как постоянный множитель.
Итак, d ² y = d ( dy )= d ( f ΄( x ) dx )=( f΄ ( x ) dx )΄ dx =( f΄ ( x ))΄( dx )²= f΄΄ ( x ) dx ². (19.3)
Подобным же образом можно найти третий дифференциал от данной функции:
d ³ y = d ( d ² y )= f΄΄΄ ( x ) d ³ x и дифференциалы более высоких порядков.
d n y = d(d n-1 y) = (f (n-1) (x)d n-1 x)΄ = f (n) (x)d n x. (19.4)
Свойства дифференциалов высших порядков.
Точки экстремума функции.
Переходя к пределу в полученных неравенствах, находим, что из первого из них следует, что f ′( x 0 ) ≥ 0, а из второго что f ′( x 0 ) ≤ 0. Следовательно, f ′( x 0 ) = 0.
Замечание 1. В теореме Ролля существенно выполнение всех трех условий. Приведем примеры функций, для каждой из которых не выполняется только одно из условий теоремы, и в результате не существует такой точки, в которой производная функции равна нулю.
Действительно, у функции, график которой изображен на рис. 1, f (0)= f ( 1 )=0, но х =1 точка разрыва, то есть не выполнено первое условие теоремы Ролля. Функция, график которой представлен на рис.2, не дифференцируема при х = 0, а для третьей функции f (- 1 )≠ f ( 1 ).
Замечание 2. Геометрический смысл теоремы Ролля: на графике рассматриваемой функции найдется по крайней мере одна точка, касательная в которой параллельна оси абсцисс.
Теоремы Лагранжа и Коши. Правило Лопиталя. Раскрытие неопределенностей.
откуда непосредственно следует утверждение теоремы.
Замечание 2. Если f ′( a )= g ′( a )= 0 и f ′( x ) и g ′( x ) удовлетворяют условиям, наложенным в теореме 20.3 на f ( x ) и g ( x ), к отношению можно еще раз применить правило Лопиталя: и так далее.
Перемножив неравенства (20.4) и (20.5), получим
, или, после использования равенства (20.3):
Формула Тейлора с остаточным членом в форме Пеано и в форме Лагранжа. Разложение основных элементарных функций по формуле Тейлора. Применение формулы Тейлора для приближенных вычислений.
Пусть искомый многочлен имеет вид:
Дополнительно вводится 0!=1.
Используя это обозначение, получим:
Таким образом, искомый многочлен имеет вид:
Формы остаточного члена в формуле Тейлора.
Применив для вычисления предела n раз правило Лопиталя, получим:
Найдем еще один вид записи R n ( x ). Представим его в виде
и определим вид функции Q ( x ). Из (21.7) следует, что
При этом предполагается, что а и х приняли фиксированные значения. Тогда
Замечание. Если в формуле Тейлора принять а = 0, этот частный случай называют формулой Маклорена :
Разложение по формуле Тейлора некоторых элементарных функций.
Отметим, что для любого х
Разложение по формуле Маклорена имеет вид:
В этом случае, как и в предыдущем, при всех значениях х
Можно предложить еще один вариант этой формулы:
Таким же образом, как и для синуса, можно получить разложение по формуле Тейлора:
f (n) (0) = m ( m 1)…( m n +1). Тогда
Применение формулы Тейлора для приближенных вычислений.
Заменяя какую-либо функцию, для которой известно разложение по формуле Тейлора, многочленом Тейлора, степень которого выбирается так, чтобы величина остаточного члена не превысила выбранное значение погрешности, можно находить приближенные значения функции с заданной точностью.
Условия возрастания и убывания функции. Экстремумы функции, необходимое условие. Достаточные условия. Отыскание наибольшего и наименьшего значений функции, дифференцируемой на отрезке.
В предыдущих лекциях использовались известные из курса элементарной математики понятия возрастающей и убывающей функций. Определим их еще раз.
Определение 22.1. Функция y = f ( x ) называется возрастающей (убывающей) на [ ab ], если
1. Пусть f ( x ) возрастает на [ ab ]. Тогда при то есть Если же поэтому Следовательно, в обоих случаях Значит, что и требовалось доказать.
Но по условию поэтому f ( x 2 ) > f ( x 1 ), следовательно, f ( x ) возрастающая функция.
Замечание 1. Аналогичную теорему можно доказать и для убывающей функции: Если f ( x ) убывает на [ ab ], то на [ ab ]. Если на ( ab ), то f ( x ) убывает на [ ab ].
Замечание 2. Геометрический смысл доказанной теоремы: если функция возрастает на отрезке [ ab ], то касательная к ее графику во всех точках на этом отрезке образует с осью Ох острый угол (или горизонтальна). Если же функция убывает на рассматриваемом отрезке, то касательная к графику этой функции образует с осью Ох тупой угол (или в некоторых точках параллельна оси Ох ).
Необходимое условие экстремума.
В лекции 19 было дано определение максимума и минимума функции.
Доказательство. Действительно, производная в точке х 0 либо существует, либо нет. Если она существует, то по теореме Ферма она равна нулю.
Замечание. Отметим еще раз, что теорема 22.2 дает необходимое, но не достаточное условие экстремума, то есть не во всех точках, в которых f ′( x ) = 0, функция достигает экстремума.
Пример. У функции y = x ³ y ′ = 3 x 2 = 0 при х = 0, однако функция монотонно возрастает во всей области определения.
Определение 22.2. Если функция определена в некоторой окрестности точки х 0 и ее производная в этой точке равна нулю или не существует, точка х 0 называется критической точкой функции. Теорема 22.1 означает, что все точки экстремума находятся в множестве критических точек функции.
Достаточные условия экстремума.
б) Если n = 2 m четное и f (2 m ) ( x 0 ) > 0, то таким же образом доказывается, что х 0 точка минимума.
Вывод : проверить наличие экстремума в критической точке можно тремя способами:
Наибольшее и наименьшее значения функции,
дифференцируемой на отрезке.
Пусть функция y = f ( x ) дифференцируема на отрезке [ ab ]. Тогда по теореме 17.2 она непрерывна на нем, и по теореме 16.2 достигает на этом отрезке своего наибольшего и наименьшего значения. Если f ( x ) имеет на [ ab ] конечное число критических точек, то ее наибольшее значение будет либо одним из ее максимумов (а именно, наибольшим максимумом), либо будет достигаться в одной из конечных точек отрезка. То же можно сказать и о наименьшем значении. Из сказанного следует, что поиск наибольшего и наименьшего значений дифференцируемой функции на отрезке можно проводить по следующей схеме:
Таким образом, наибольшее значение функции на рассматриваемом отрезке равно 61 и принимается на его правой границе, а наименьшее равно 20 и достигается в точке минимума внутри отрезка.
Исследование выпуклости функции. Точки перегиба, их нахождение. Асимптоты функций. Общая схема исследования функции и построения ее графика.
Определение 23.1. Кривая называется выпуклой (обращенной выпуклостью вверх) на интервале ( ab ), если все точки кривой лежат ниже любой ее касательной на этом интервале.
Например, кривая, изображенная на рисунке, выпукла на интервале (ВС) и вогнута на интервале (АВ).
Доказательство. Докажем первое утверждение теоремы. Пусть f ′′( x ) ab ).
Второе утверждение теоремы доказывается аналогичным образом.
Замечание. Если в точке перегиба существует касательная к кривой, то в этой точке она пересекает кривую, потому что по одну сторону от данной точки кривая проходит выше касательной, а по другую ниже.
Замечание. Можно доказать, что если в условиях теоремы 22.5 критическая точка не является точкой экстремума, то она является точкой перегиба.
Рассмотрим три вида асимптот и определим способы их нахождения.
Замечание. Число вертикальных асимптот графика функции не ограничено, а наклонных и горизонтальных в сумме может быть не более двух (при и при ).
Общая схема исследования функции.
Результаты, полученные при изучении различных аспектов поведения функции, позволяют сформулировать общую схему ее исследования с целью построения качественного графика, отражающего характерные особенности поведения данной функции. Для этого требуется определить:
Заметим, что подробный ответ на первый вопрос фактически содержит ответы на второй и отчасти на седьмой вопросы. Действительно, если в область определения не входят отдельно расположенные точки и найдены односторонние пределы функции в этих точках, то тем самым указан характер разрывов. В частности, если какой-либо из этих односторонних пределов бесконечен, через точку разрыва (или через соответствующую границу области определения) проходит вертикальная асимптота. Если область определения функции не ограничена слева или справа и на бесконечности соответствующего знака существует конечный предел функции, то график имеет на указанном конце оси Ох горизонтальную асимптоту.
Пример. Исследуем функцию и построим ее график.
Построим график функции на основе результатов проведенного исследования.
Будь умным!
Работа добавлена на сайт samzan.ru: 2016-03-13
Производные и дифференциалы высших порядков, их свойства. Точки экстремума функции. Теоремы Ферма и Ролля.
Свойства производных высших порядков.
Основные свойства производных высших порядков следуют из соответствующих свойств первой производной:
Заметим, что коэффициенты в этой формуле совпадают с соответствующими коэффициентами формулы бинома Ньютона, если заменить производные данного порядка той же степенью переменной. Для n =1 эта формула была получена при изучении первой производной, для производных высших порядков ее справедливость можно доказать с помощью метода математической индукции.
Дифференциалы высших порядков.
Обозначение: d ² y = d ( dy ).
При вычислении второго дифференциала учтем, что dx не зависит от х и при дифференцировании выносится за знак производной как постоянный множитель.
Итак, d ² y = d ( dy )= d ( f ΄( x ) dx )=( f΄ ( x ) dx )΄ dx =( f΄ ( x ))΄( dx )²= f΄΄ ( x ) dx ². (19.3)
Подобным же образом можно найти третий дифференциал от данной функции:
d ³ y = d ( d ² y )= f΄΄΄ ( x ) d ³ x и дифференциалы более высоких порядков.
d n y = d(d n-1 y) = (f (n-1) (x)d n-1 x)΄ = f (n) (x)d n x. (19.4)
Свойства дифференциалов высших порядков.
Точки экстремума функции.
Переходя к пределу в полученных неравенствах, находим, что из первого из них следует, что f ′( x 0 ) ≥ 0, а из второго что f ′( x 0 ) ≤ 0. Следовательно, f ′( x 0 ) = 0.
Замечание 1. В теореме Ролля существенно выполнение всех трех условий. Приведем примеры функций, для каждой из которых не выполняется только одно из условий теоремы, и в результате не существует такой точки, в которой производная функции равна нулю.
Действительно, у функции, график которой изображен на рис. 1, f (0)= f ( 1 )=0, но х =1 точка разрыва, то есть не выполнено первое условие теоремы Ролля. Функция, график которой представлен на рис.2, не дифференцируема при х = 0, а для третьей функции f (- 1 )≠ f ( 1 ).
Замечание 2. Геометрический смысл теоремы Ролля: на графике рассматриваемой функции найдется по крайней мере одна точка, касательная в которой параллельна оси абсцисс.
Теоремы Лагранжа и Коши. Правило Лопиталя. Раскрытие неопределенностей.
откуда непосредственно следует утверждение теоремы.
Замечание 2. Если f ′( a )= g ′( a )= 0 и f ′( x ) и g ′( x ) удовлетворяют условиям, наложенным в теореме 20.3 на f ( x ) и g ( x ), к отношению можно еще раз применить правило Лопиталя: и так далее.
Перемножив неравенства (20.4) и (20.5), получим
, или, после использования равенства (20.3):
Формула Тейлора с остаточным членом в форме Пеано и в форме Лагранжа. Разложение основных элементарных функций по формуле Тейлора. Применение формулы Тейлора для приближенных вычислений.
Пусть искомый многочлен имеет вид:
Дополнительно вводится 0!=1.
Используя это обозначение, получим:
Таким образом, искомый многочлен имеет вид:
Формы остаточного члена в формуле Тейлора.
Применив для вычисления предела n раз правило Лопиталя, получим:
Найдем еще один вид записи R n ( x ). Представим его в виде
и определим вид функции Q ( x ). Из (21.7) следует, что
При этом предполагается, что а и х приняли фиксированные значения. Тогда
Замечание. Если в формуле Тейлора принять а = 0, этот частный случай называют формулой Маклорена :
Разложение по формуле Тейлора некоторых элементарных функций.
Отметим, что для любого х
Разложение по формуле Маклорена имеет вид:
В этом случае, как и в предыдущем, при всех значениях х
Можно предложить еще один вариант этой формулы:
Таким же образом, как и для синуса, можно получить разложение по формуле Тейлора:
f (n) (0) = m ( m 1)…( m n +1). Тогда
Применение формулы Тейлора для приближенных вычислений.
Заменяя какую-либо функцию, для которой известно разложение по формуле Тейлора, многочленом Тейлора, степень которого выбирается так, чтобы величина остаточного члена не превысила выбранное значение погрешности, можно находить приближенные значения функции с заданной точностью.
Условия возрастания и убывания функции. Экстремумы функции, необходимое условие. Достаточные условия. Отыскание наибольшего и наименьшего значений функции, дифференцируемой на отрезке.
В предыдущих лекциях использовались известные из курса элементарной математики понятия возрастающей и убывающей функций. Определим их еще раз.
Определение 22.1. Функция y = f ( x ) называется возрастающей (убывающей) на [ ab ], если
1. Пусть f ( x ) возрастает на [ ab ]. Тогда при то есть Если же поэтому Следовательно, в обоих случаях Значит, что и требовалось доказать.
Но по условию поэтому f ( x 2 ) > f ( x 1 ), следовательно, f ( x ) возрастающая функция.
Замечание 1. Аналогичную теорему можно доказать и для убывающей функции: Если f ( x ) убывает на [ ab ], то на [ ab ]. Если на ( ab ), то f ( x ) убывает на [ ab ].
Замечание 2. Геометрический смысл доказанной теоремы: если функция возрастает на отрезке [ ab ], то касательная к ее графику во всех точках на этом отрезке образует с осью Ох острый угол (или горизонтальна). Если же функция убывает на рассматриваемом отрезке, то касательная к графику этой функции образует с осью Ох тупой угол (или в некоторых точках параллельна оси Ох ).
Необходимое условие экстремума.
В лекции 19 было дано определение максимума и минимума функции.
Доказательство. Действительно, производная в точке х 0 либо существует, либо нет. Если она существует, то по теореме Ферма она равна нулю.
Замечание. Отметим еще раз, что теорема 22.2 дает необходимое, но не достаточное условие экстремума, то есть не во всех точках, в которых f ′( x ) = 0, функция достигает экстремума.
Пример. У функции y = x ³ y ′ = 3 x 2 = 0 при х = 0, однако функция монотонно возрастает во всей области определения.
Определение 22.2. Если функция определена в некоторой окрестности точки х 0 и ее производная в этой точке равна нулю или не существует, точка х 0 называется критической точкой функции. Теорема 22.1 означает, что все точки экстремума находятся в множестве критических точек функции.
Достаточные условия экстремума.
б) Если n = 2 m четное и f (2 m ) ( x 0 ) > 0, то таким же образом доказывается, что х 0 точка минимума.
Вывод : проверить наличие экстремума в критической точке можно тремя способами:
Наибольшее и наименьшее значения функции,
дифференцируемой на отрезке.
Пусть функция y = f ( x ) дифференцируема на отрезке [ ab ]. Тогда по теореме 17.2 она непрерывна на нем, и по теореме 16.2 достигает на этом отрезке своего наибольшего и наименьшего значения. Если f ( x ) имеет на [ ab ] конечное число критических точек, то ее наибольшее значение будет либо одним из ее максимумов (а именно, наибольшим максимумом), либо будет достигаться в одной из конечных точек отрезка. То же можно сказать и о наименьшем значении. Из сказанного следует, что поиск наибольшего и наименьшего значений дифференцируемой функции на отрезке можно проводить по следующей схеме:
Таким образом, наибольшее значение функции на рассматриваемом отрезке равно 61 и принимается на его правой границе, а наименьшее равно 20 и достигается в точке минимума внутри отрезка.
Исследование выпуклости функции. Точки перегиба, их нахождение. Асимптоты функций. Общая схема исследования функции и построения ее графика.
Определение 23.1. Кривая называется выпуклой (обращенной выпуклостью вверх) на интервале ( ab ), если все точки кривой лежат ниже любой ее касательной на этом интервале.
Например, кривая, изображенная на рисунке, выпукла на интервале (ВС) и вогнута на интервале (АВ).
Доказательство. Докажем первое утверждение теоремы. Пусть f ′′( x ) ab ).
Второе утверждение теоремы доказывается аналогичным образом.
Замечание. Если в точке перегиба существует касательная к кривой, то в этой точке она пересекает кривую, потому что по одну сторону от данной точки кривая проходит выше касательной, а по другую ниже.
Замечание. Можно доказать, что если в условиях теоремы 22.5 критическая точка не является точкой экстремума, то она является точкой перегиба.
Рассмотрим три вида асимптот и определим способы их нахождения.
Замечание. Число вертикальных асимптот графика функции не ограничено, а наклонных и горизонтальных в сумме может быть не более двух (при и при ).
Общая схема исследования функции.
Результаты, полученные при изучении различных аспектов поведения функции, позволяют сформулировать общую схему ее исследования с целью построения качественного графика, отражающего характерные особенности поведения данной функции. Для этого требуется определить:
Заметим, что подробный ответ на первый вопрос фактически содержит ответы на второй и отчасти на седьмой вопросы. Действительно, если в область определения не входят отдельно расположенные точки и найдены односторонние пределы функции в этих точках, то тем самым указан характер разрывов. В частности, если какой-либо из этих односторонних пределов бесконечен, через точку разрыва (или через соответствующую границу области определения) проходит вертикальная асимптота. Если область определения функции не ограничена слева или справа и на бесконечности соответствующего знака существует конечный предел функции, то график имеет на указанном конце оси Ох горизонтальную асимптоту.
Пример. Исследуем функцию и построим ее график.
Построим график функции на основе результатов проведенного исследования.
Дифференциалы высших порядков.
Пусть функция у= ¦(х) определена в некотором промежутке Х (например, интервале) и имеет в каждой внутренней точке производные всех порядков. Тогда ее дифференциал dу=у 1 dх. Будем называть ее дифференциалом первого порядка.
В каждой конкретной точке дифференциал функции есть число. На промежутке он есть функция от х. Поэтому можно говорить о дифференциале от первого дифференциала.
Определение: Дифференциал от дифференциала первого порядка функции у= ¦(х) называют дифференциалом второго порядка этой функции и символически записывают d(dу)=d 2 у.
Вообще: дифференциалом n-го порядка функции у= ¦(х) называют дифференциал от дифференциала (n-1) порядка функции d n у= d(d n-1 у).
Дифференциалы порядка выше первого называются дифференциалами высших порядков.
При вычислении дифференциалов высших порядков нужно учитывать, что dх есть произвольное, но не зависящее от х число и при дифференцировании по х нужно считать постоянным множителем.
Здесь снова dх 3 = dх dх dх, а не d(х 3 )=3х 2 dх
Здесь dх n = (dх) n по прежнему.
Из общей формулы дифференциала n-го порядка в частности следует формула производной n-го порядка.
Мы видели, что форма первого дифференциала dу=у 1 dх не зависит от того, является ли х независимым переменным или х является сама функцией от некоторой переменной t.
Форма дифференциала порядка n=2 уже не сохраняется в этом случае, она не обладает инвариантностью.
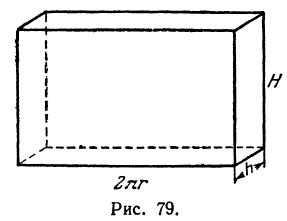
В случае независимой переменной х d 2 у=у 11 dх 2 –дифференциал второго порядка. Пусть теперь х= 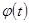
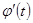
d 2 у= d (у 1 dх) = d (у 1 )dх+ у 1 d (dх)= у 11 dх 2 + у 1 d 2 х, т.е.
d 2 у= у 11 dх 2 + у 1 d 2 х – форма дифференциала изменилась, добавилось слагаемое у 1 d 2 х. Тем более не сохраняется форма d n у. Значит, в случае, когда х не есть независимая переменная обозначение у (п) = d п у/ dх п следует понимать, как единый символ, а не как отношение дифференциалов.
Дифференциал функции в математике с примерами решения и образцами выполнения
Понятие дифференциала функции:
Известно, что если функция 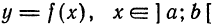
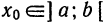
где функция 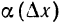
Слагаемое 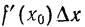
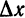
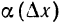
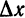
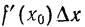
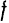
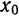
Определение:
Дифференциалом функции 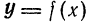
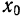
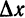
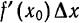
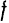
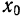
Дифференциал функции обозначается 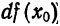
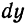
Пример:
Найти дифференциал функции 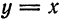
Решение:
По формуле (3) имеем:
Итак, дифференциал 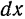
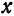
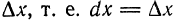
Пример:
Найти дифференциал сложной функции 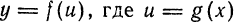
Решение:
По формуле (4) находим:
Но — 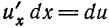
Таким образом, форма дифференциала не зависит от того, является аргумент данной функции независимой переменной или функцией другого аргумента. Это свойство дифференциала сложной функции называется инвариантностью формы дифференциала.
Пример:
Найти дифференциал функции
Решение:
По формуле (4) находим:
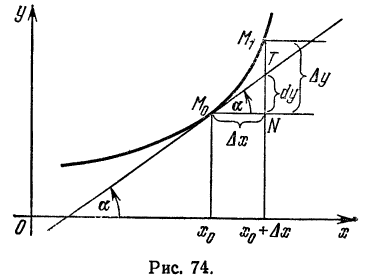
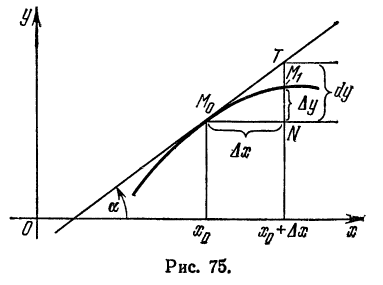
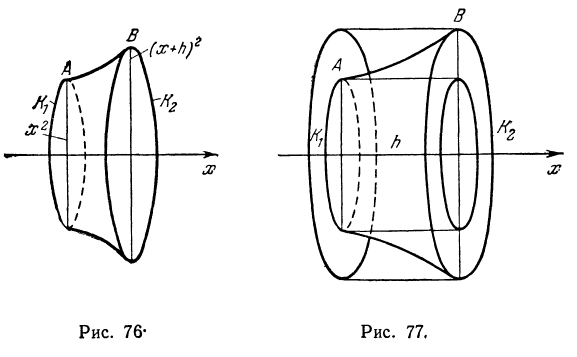
Геометрический смысл дифференциала
Пусть 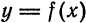
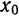
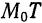
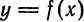
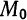
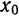
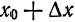
Из прямоугольного треугольника 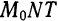
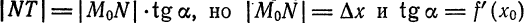
Таким образом, дифференциал функции 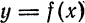
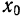
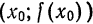
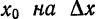
Можно показать, что этот вывод не зависит от расположения графика функции и касательной на координатной плоскости.
Дифференциал может быть как меньше приращения функции (см. рис. 74), так и больше (рис. 75). Однако при достаточно малых приращениях 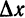
принять 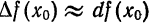
Вычисление дифференциала
Мы установили, что дифференциал функции 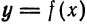
т. е. дифференциал функции 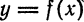
По формуле (1) можно вычислить дифференциал любой дифференцируемой функции. Так, например;
Аналогично, каждой из основных формул дифференцирования можно сопоставить соответствующую формулу для вычисления дифференциала.
Пример:
Найти дифференциал функции
Решение:
По формуле (1) находим:
Пример:
Найти дифференциал функции
Решение:
Находим:
Дифференциалы высших порядков
Из формулы 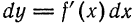
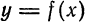
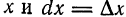
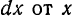
Рассмотрим дифференциал 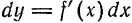
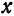
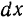
Дифференциал от дифференциала функции 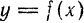
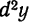
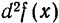
Таким образом,
Принято скобки при степенях 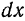
Аналогично определяются дифференциалы третьего порядка:
Вообще, дифференциалом п-го порядка называется дифференциал от дифференциала 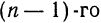
Таким образом, для нахождения дифференциала п—го порядка функции 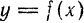
Пример:
Найти дифференциалы первого, второго и третьего порядка функции
Решение:
Находим соответствующие производные
от данной функции:
Приложение дифференциала приближенным вычислениям
Рассмотрим функцию 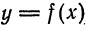
Выше (§ 2) было установлено, что при достаточно малых 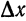
Так как вычислять 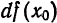
Вычисление приближенного значения приращения функции
Пример:
Найти приближенное значение приращения функции 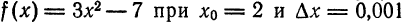
Решение:
Применив формулу (3), получим:
Посмотрим, какую погрешность мы допустили, вычислив дифференциал данной функции вместо ее приращения. Для этого найдем истинное значение приращения:
Далее, находим абсолютную погрешность приближения:
а затем и относительную погрешность:
Погрешность приближения оказалась довольно малой, что еще раз подтверждает целесообразность применения формулы (3).
Вычисление приближенного числового значения функции
Из формулы (1) имеем
Пример:
Найти приближенное значение функции
Решение:
Представим 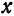
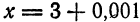
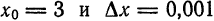
Приближенное вычисление степеней
Рассмотрим функцию 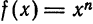
По этой формуле наводят приближенное значение степеней.
Пример:
Найти приближенное значение степени 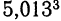
Решение:
Представим данную степень в виде 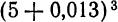
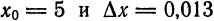
(5) найдем:
Приближенное извлечение корней
При 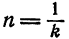
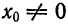
Формула (6), известная и по школьному курсу, дает возможность найти приближенные значения различных корней.
Пример:
Найти приближенное значение корня
Решение:
Представим данный корень в виде 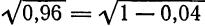
Дополнение к дифференциалу





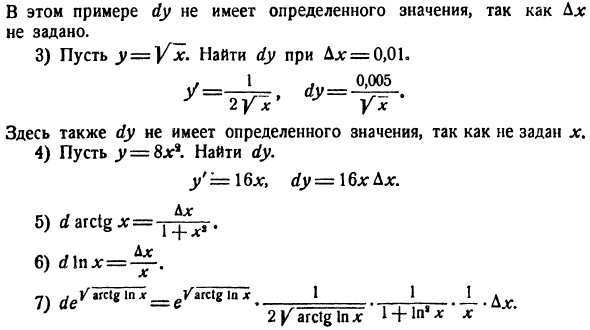



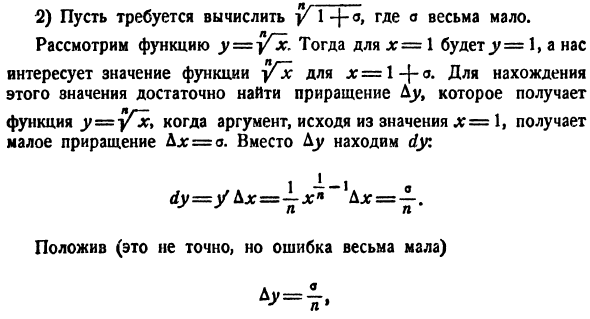




Понятие о дифференциале в высшей математике
Сравнение бесконечно малых величин между собой
I. Мы рассмотрели действия над бесконечно малыми величинами и показали, что в результате сложения, вычитания и умножения их получаются также бесконечно малые величины. Однако частное от деления двух бесконечно малых друг на друга может быть не только бесконечно малой величиной, но и бесконечно большой и конечной.
В самом деле, пусть, например, а — бесконечно малая, тогда 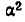
1) отношение 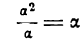
2) отношение 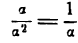
3) отношение 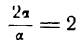
Первое отношение показывает, что бесконечно малая 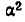
Второе отношение указывает на то, что а, неограниченно уменьшаясь, остается значительно больше, чем 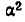
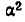
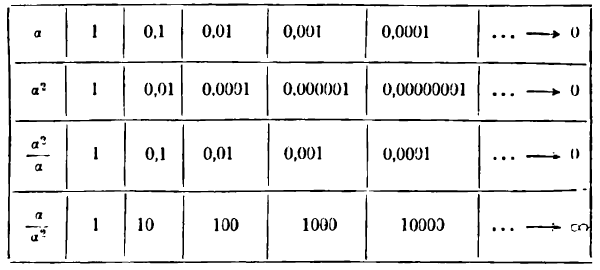
Сказанное можно иллюстрировать следующей таблицей:
Принято бесконечно малую 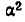
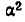
Что касается третьего отношения, то из него следует, что бесконечно малые 2а и а стремятся к нулю с одинаковой скоростью, так как при их изменении отношение 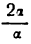
Таким образом, частное от деления двух бесконечно малых величин позволяет сравнивать их между собой. Это сравнение особенно полезно в приближенных вычислениях, где отбрасывание бесконечно малых высшего порядка приводит к значительному упрощению вычислений.
II. Возьмем функцию 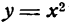
Множитель при 
Сравним изменение величины обоих слагаемых правой части равенства (I) с уменьшением 
х = 2 и, следовательно, у’ = 4, составим следующую таблицу значений этих слагаемых:
Как видно из таблицы, слагаемые у’ 
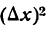


Покажем, что то же самое справедливо для любой дифференцируемой функции f(x).
Пусть дана функция у = f(х). Ее производная
Согласно определению предела переменной имеем:
где а—бесконечно малая величина при 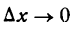
И здесь при уменьшении 



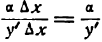
малая величина при 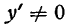



Определение:
Главная часть у’ 
Дифференциал функции у = f(х) принято обозначать символом dу. Таким образом
Дифференциал аргумента dх принимают равным приращению аргумента 
Поэтому равенство (3) можно переписать в следующем виде:
т. е. дифференциал функции равен произведению производной функции на дифференциал аргумента. Из формулы (4) следует:
Равенство (5) показывает, что производная функции есть отношение дифференциала функции к дифференциалу аргумента. На этом основании производную функции часто выражают в виде 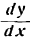
III. Заменив в равенстве (2) 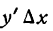
Как было показано выше, 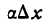
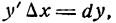
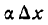
В практических вопросах часто используют формулу (7), т. е. берут дифференциал функции вместо ее приращения, делая при этом незначительную ошибку и тем меньшую, чем меньше 
Примечание:
В случае линейной функции 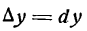
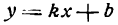
Множитель 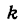
Итак, в случае линейной функции
Геометрическое изображение дифференциала
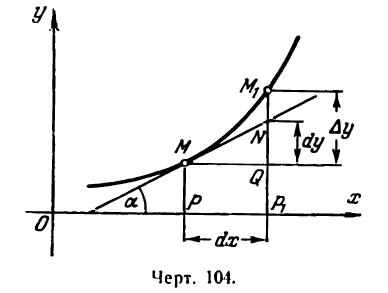
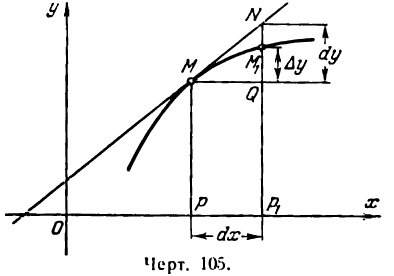
Возьмем функцию у = f(x), график которой изображен на рис. 104.
Пусть абсцисса точки М
Дадим аргументу х приращение 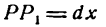
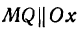
Проведем в точке М касательную к кривой; полученный при этом отрезок QN, равный приращению ординаты точки М, движущейся по касательной, называется приращением ординаты касательной. Из прямоугольного треугольника МQN имеем:
а, согласно геометрическому смыслу производной,
Таким образом, если в точке М кривой у = f(х) провести касательную, то дифференциал функции у = f(х) в этой
точке изобразится приращением ординаты касательной, соответствующим приращению ее абсциссы на dx.
Дифференциал функции в данной точке может быть как меньше приращения ее (рис. 104), так и больше (рис. 105).
Дифференциал второго порядка
Дифференциал dy функции у = f(x), называемый первым дифференциалом или дифференциалом первого порядка, представляет собой также функцию x, а потому и от него можно найти дифференциал, который называют вторым дифференциалом или дифференциалом второго порядка. В этом случае пишут d(dy) или короче 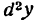
Найдем выражение дифференциала второго порядка от функции через ее производную. Для этого продифференцируем по х равенство.
считая dx постоянным множителем (так как dx не зависит от х):
Но согласно формуле (4)
т. е. дифференциал второго порядка равен произведению второй производной функции на квадрат дифференциала аргумента.
Из равенства (1) следует
Это дает основание для выражения второй производной
функции в виде отношения 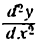
Приложение дифференциала к приближенным вычислениям
Рассмотрим несколько примеров использования дифференциала в приближенных вычислениях.
а) Определение приращения функции.
Пример:
Найти приближенно приращение функции
при х = 2 и 
Решение:
Так как приращение аргумента — величина малая, то согласно формуле (7) можем приращение функции заменить ее дифференциалом.
Дифференциал же данной функции
Заменив в равенстве (1) х и dх их значениями, получим:
Посмотрим, какую ошибку мы делаем, беря дифференциал вместо приращения. Для этого найдем точное значение приращения функции:
Сравнивая полученное точное значение 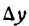
Ошибка оказалась очень малой.
Пример:
Шар радиуса R = 20 см был нагрет, отчего радиус его удлинился на 0,01 см. Насколько увеличился при этом объем шара?
Решение:
Объем шара определяется по формуле
Каждому значению R по закону, заданному этой формулой, отвечает одно определенное значение v, т. е. v есть функция от R. Следовательно, наша задача сводится к определению приращения функции v при заданном приращении аргумента R. Так как приращение аргумента мало
то мы можем приращение функции заменить ее дифференциалом.
Находим дифференциал функции v.
б) Нахождение числового значения функции. Пусть требуется найти приближенное значение функции
при x1 = 2,001, т. е. найти величину f(2,001). Представим х1 в виде суммы
где 0,001 будем рассматривать как приращение аргумента. Из формулы для приращения функций
Полагая 
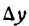
Применив равенство (2) к данному примеру, можем написать:
Равенство (2) может служить формулой для приближенного вычисления значения функции.
в) Вычисление по приближенным формулам. Пользуясь формулой (2), выведем приближенные формулы для вычисления некоторых выражений. 1) Возьмем функцию
и положим, что угол х, равный нулю, получает весьма малое приращение а. Применим формулу (2), полагая в ней х = 0 и dx = а. Получим:
Отсюда следует, что синус очень малого угла приближенно равен самому углу; при этом нужно помнить, что угол должен быть выражен в радианной мере. Так, например, sin 0,003 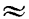
2) Возьмем функцию 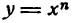
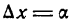
Точно так же можно вывести равенство
По формулам (3) и (4) можно быстро найти приближенную степень числа, близкого к единице; например:
3) Выведем формулу для приближенного вычисления выражения 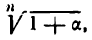
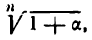
Аналогично выводится формула
По формулам (5) и (6) можно легко найти приближенное значение корня из числа, близкого к единице; например:
Кривизна кривой
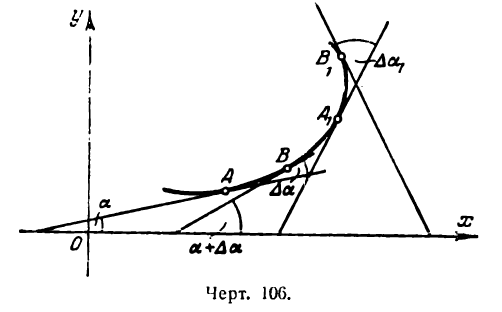
Пусть дана кривая, определяемая уравнением у = f(х) (рис. 106).
Возьмем на ней две точки А и В и проведем в них касательные к кривой. При переходе от точки А к точке В касательная меняет угол наклона к положительному направлению оси абсцисс на некоторую величину. Если обозначим угол наклона касательной в точке А к оси Ох через а, то угол наклона касательной в точке В к той же оси, получив приращение 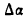
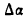
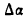
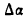
Разделив 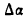
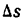
Средняя кривизна кривой на разных ее участках может быть различной.
Допустим теперь, что точка В, двигаясь по кривой, неограниченно приближается к точке А и 
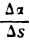
Определение:
Кривизной кривой в данной ее точке А называется предел, к которому стремится средняя кривизна дуги АВ при неограниченном приближении точки В к А.
Согласно определению производной
Преобразуем правую часть этого равенства, выразив dа. и ds через производные данной функции у =f(x).
Согласно геометрическому смыслу производной имеем
где а — угол наклона касательной к кривой у =f(х) в точке А к положительному направлению оси абсцисс (рис. 106); отсюда
В этом равенстве аrctg у’ — функция от функции, так как аrctg у’ зависит от у’, a у’ зависит от х. Продифференцируем последнее равенство по аргументу х; получим:
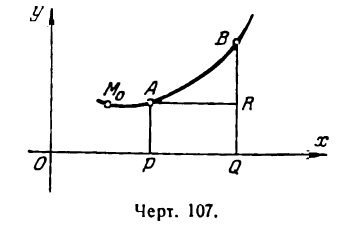
Найдем выражение ds через производную функции у =f(x). Для этого возьмем снова тот же участок АВ кривой (рис. 107).
Будем рассматривать длину АВ как приращение дуги 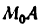

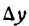

Разделив обе части равенства на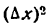
Положим, что 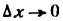
поэтому равенство (3) примет вид
Подставив значение da и ds в выражение (1), получим:
Формула (5) позволяет найти кривизну кривой, определяемой уравнением у = f(x), в любой ее точке.
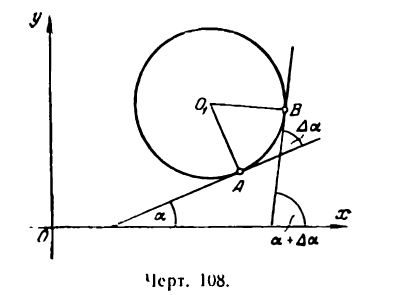
Кривизна окружности
Проведем касательные в двух точках А и В окружности (рис. 108).
Обозначив дугу АВ через 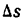
на этом участке; она выразится дробью 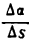
так как углы АО1В и 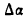
Ясно, что такой же вывод мы получим, взяв другой какой-либо участок окружности. Следовательно,
для любой точки окружности, т. е. кривизна окружности постоянна во всех ее точках и равна обратной величине ее радиуса.
Радиус кривизны кривой
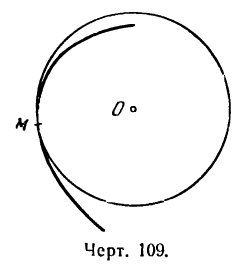
При изучении кривизны кривой подбирают такую окружность, кривизна которой равна кривизне кривой в той или иной ее точке. Центр этой окружнoсти называется центром кривизны кривой в соответствующей точке, радиус—радиусом кривизны кривой в этой точке, а сама окружность— окружностью кривизны (рис. 109).
Определение:
Окружностью кривизны в точке М кривой называется окружность, проходящая через точку М и имеющая с кривой одинаковую кривизну и общую касательную.
Заметим, что центр окружности кривизны всегда располагается со стороны вогнутости кривой.
Кривизна окружности, как мы знаем,
Следовательно, и радиус кривизны кривой в точке ее определяется тем же равенством.
Применяя эту формулу к прямой линии, заданной, например уравнением 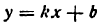
так как
Это значит, что прямую линию можно рассматривать как окружность бесконечно большого радиуса.
Пример:
Найти радиус кривизны кривой 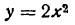
Решение:
Найдем сначала первую и вторую производные функции 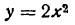
Подставив значения у’ и у» в формулу (1), получим:
Как найти дифференциал — подробная инструкция
Бесконечно малые величины
Бесконечно малые величины 
Определение:
Бесконечно малой величиной вблизи h = a называется функция, зависящая от h и имеющая предел, равный нулю при условии, что независимое переменное стремится к а.
Например, 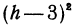
Приведем примеры геометрического и физического содержания.
Пример:
Площадь S прямоугольника со сторонами х и h является бесконечно малой при любых х, так как
Пример:
Объема прямоугольного параллелепипеда, ребра которого равны 3, 2 и 2h, является бесконечно малым, так как
Пример:
Объем v прямоугольного параллелепипеда, ребра которого равны h, 2h и 5h, является бесконечно малым, так как
Пример:
По закону Ома v = Ri, где v — напряжение, R — сопротивление и i — ток. Отсюда следует, что при постоянном сопротивлении напряжение является бесконечно малым относительно тока, так как
Пусть дана бесконечно малая величина а (h), т. е.
Рассмотрим предел отношения
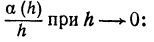
Если этот предел существует и равен нулю, то бесконечно малая величина a (h) называется бесконечно малой более высокого порядка, чем h.
Если предел равен конечному числу 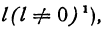
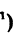
Пример:
Пусть 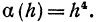
Пример:
Пример:
Пример:
В заключение параграфа рассмотрим функцию y = f(x). Пусть приращение независимого переменного равно А, тогда приращение функции равно
Пример:
Пусть дана функция 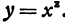
Если же x = 0 и по-прежнему h =1, то
Здесь h сохраняет значение 1, но, поскольку х меняется, изменяется и 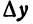
Если же x = 2, а h = 0,5, то
Здесь х сохраняет значение 2, но h меняется, поэтому меняется и 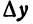
Если f(х)—функция непрерывная, то, по определению, ее приращение 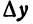
Дифференциал
Пусть дана непрерывная функция у = f(х), имеющая производную. Тогда, по определению производной,
Очевидно, что первый член
Из равенства (4) получаем, что приращение функции с точностью до бесконечно малой высшего порядка равно f'(х)h ; это выражение называется дифференциалом функции.
Определение. Дифференциал есть та часть при-ращения функции 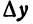
Дифференциал функции обозначают или dy, или df(x), так что
Для симметрии записей вводится определение дифференциала независимого переменного.
Определение:
Дифференциалом независимого переменного называется его приращение.
Дифференциал независимого переменного обозначается dx, так что имеем
Операция нахождения дифференциала называется дифференцированием.
Пример:
Найдем дифференциал функции у = sin х. Так как (sin х)’ = cos х, то dy = dsin х = cos х • h = cos xdx.
Пример:
Подставляя сюда вместо х его значение 2, а вместо dx его значение 0,1, получим
Из определения дифференциала функции следует, что дифференциал функции одного переменного является функцией двух переменных. Из формул (5) и (6) следует, что
Таким образом, производная равна отношению дифференциала функции к дифференциалу независимого переменного.
С этого момента для обозначения производной будем пользоваться и знаком ( )’ и отношением дифференциалов.
Таблица дифференциал
Применение к приближенным вычислениям
Перепишем формулу (4) § 2 в следующем виде:
и для начала посмотрим на примере, как будут выглядеть отдельные ее члены при некоторых числовых значениях х и h.
Пример:
Пусть 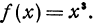
С другой стороны, применяя формулу (1) и зная, что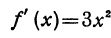
Сравнивая формулы (*) и (**), видим, что в левых частях стоит одно и то же, в правых же частях совпадают первые два члена, следовательно, третий член в формуле (**) равен двум последним членам в формуле (*), т. е.
Вычислим все члены, встречающиеся в этом примере, при указанных числовых значениях х и h:
Если бы мы захотели вычислить 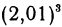
(знак 
Приведем примеры применения формулы (2).
Пример:
Выведем приближенную формулу для вычисления кубического корня. Возьмем 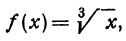
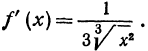
Если положить 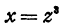
Отсюда видно, что если нам известен кубический корень из числа, то для близких чисел можно с удобством воспользоваться выведенной формулой. Например, зная, что 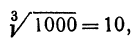
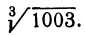
Сделаем проверку, возведя 10,01 в куб. Видим, что вместо 1003 получили число 1003,003001, т. е. ошибка меньше 0,005.
Пример:
Выведем приближенную формулу для вычисления тангенсов малых углов. Так как 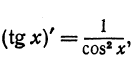
Зная, что tg 0 = 0 и cos 0=1, и полагая в предыдущей формуле x = 0, найдем
Напоминаем, что здесь h есть радианная мера угла. Например, вычислим tg3°. Переведем сначала градусную меру угла в радианную:
Дифференциал площади криволинейной трапеции
Определение:
Криволинейной трапецией называется плоская фигура, ограниченная с трех сторон прямыми, а с четвертой стороны кривой. При этом две прямые параллельны между собой и перпендикулярны третьей, а кривая пересекается с любой прямой, параллельной боковым сторонам, в одной точке.
Не исключается случай, когда одна или обе боковые стороны обращаются в точку. На рис. 69, 70, 71 изображены криволинейные трапеции.
Все плоские фигуры, с которыми нам придется встречаться, могут быть представлены как совокупность криволинейных трапеций. Например, на рис. 72 фигура разбита на четыре криволинейные трапеции.
Конечная наша цель — определить площадь криволинейной трапеции, но пока эту задачу мы еще не можем решить. Однако мы сумеем найти дифференциал площади криволинейной трапеции. Решим эту задачу, предполагая, что трапеция расположена определенным образом.
Пусть дана криволинейная трапеция АВСD, ограниченная осью Ох, двумя прямыми, перпендикулярными этой оси, и кривой, заданной уравнением у=f(х) (рис. 73).
Будем считать, что прямая АВ неподвижна в процессе всех рассуждений, т. е. абсцисса точки А есть постоянная величина. «Прямую же СD будем двигать, т. е. абсцисса точки D будет переменной. Обозначим ее через х.
Ясно, что площадь криволинейной трапеции АВСD будет изменяться в зависимости от величины х, значит, площадь есть функция х. Обозначим ее F(х). Этой функции мы не знаем, но несмотря на это найдем ее дифференциал.
Дадим х приращение h = DК, тогда площадь F(x) получит приращение 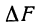
При изменении независимого переменного от величины х до х + h (от точки D) до точки К) функция f(х), т. е. ордината точки, лежащей на кривой, также изменяется и при этом достигает наибольшего значения М и наименьшего значения т. На рис. 73 QR = М и NР= т.
Обозначим разность между приращением 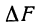
Остановимся на формуле (1) и проследим, как меняются ее члены при стремлении h к нулю.
Предварительно заметим, что, во-первых, всегда, т. е. при любых значениях x,
и, во-вторых, если 
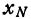

Функция f(х) предполагается непрерывной. В силу свойств непрерывной функции (см. гл. VI, § 6) находим
а это значит, что можно записать (см. начало § 2 этой главы)
где а—бесконечно малая относительно h. Также можно заключить, что
где 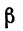
Исследуем порядок малости членов, стоящих в правой части равенства (1). Для этого найдем следующие пределы:
Первый предел находим непосредственно [применяя (3)]:
Чтобы найти второй предел, найдем сначала [используя (4) и (5)]
Так как 
а в силу равенства (7)
Таким образом, установлено, что и mh и 
Учитывая все эти рассуждения и применяя равенство (4), можно переписать равенство (1) в виде
В правой части равенства (8) стоят три члена. Каждый из них является бесконечно малым относительно h первый из них линеен относительно h, а два других имеют высший порядок малости.
Этим результатом мы воспользуемся в следующих главах.
Пример:
Найдем дифференциал площади F криволинейной трапеции, ограниченной осью Ох, кривой, заданной уравнением 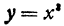
Применяя только что полученный результат, будем иметь
Пример:
Найти производную от площади криволинейной трапеции, ограниченной осью Ох, кривой, заданной уравнением у = sin x, прямой х = 2 и подвижной прямой, параллельной оси Оу.
Находим дифференциал этой площади: dF = sin x dx, а следовательно и производную:
Применение дифференциала к различным задачам
Рассуждения не только приводят к понятию дифференциала, но в некоторых случаях позволяют найти производную. Предположим, что приращение некоторой функции представлено в виде
где 
т. е. 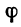
Пример:
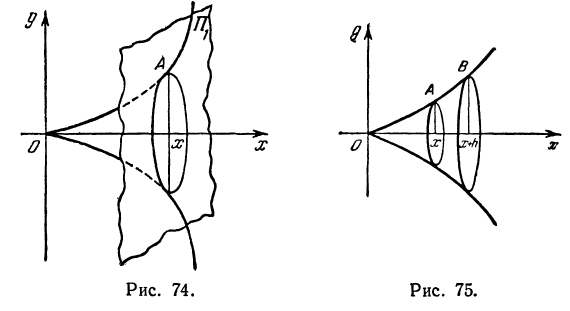
Найти производную от функции f(x), определенной геометрически как объем, ограниченный:
1) поверхностью Р, полученной от вращения вокруг оси Ох дуги ОА, принадлежащей параболе 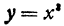
2) плоскостью П1, перпендикулярной оси Ох и отстоящей от начала координат на расстояние х (рис. 74).
Рассмотрим два цилиндра: первый из них имеет основанием К1, образующую, параллельную оси Ох, и высоту h, второй имеет основанием К2 и образующую, также параллельную оси Ох (рис. 77).
Но oбъемы W1 и W2 легко подсчитать:
Разность объемов W1 и W2 (т. е. объем цилиндрического кольца) равна
Приращение 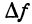
где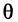
то член 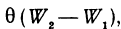
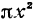
В этом примере следует обратить внимание на то, что функция f(х) была определена чисто геометрически, нам не была известна формула, определяющая эту функцию, однако производную мы нашли.
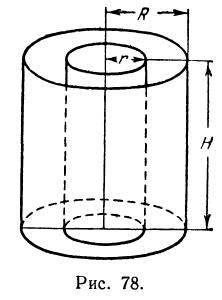
Пример:
Рассмотрим цилиндрическую трубу, у которой радиус внешней поверхности R, радиус внутренней поверхности r, высота H. Найдем объем V материала, из которого сделана эта труба (рис. 78).
Будем называть этот объем объемом цилиндрического слоя. Поскольку объем внешнего цилиндра равен 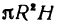
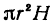
Если стенка трубы тонкая, то r и R мало отличаются друг от друга. Обозначим их разность через h (h = R — r). Тогда формула (*) примет вид
Второй член, стоящий в правой части равенства (*), второго порядка относительно h. Поэтому при 
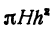
Интересно отметить еще один способ получения этой формулы (рис. 79).
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института