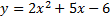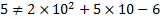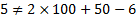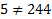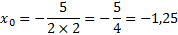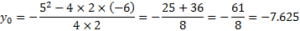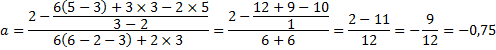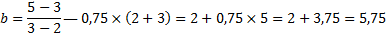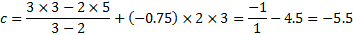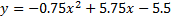Как находятся координаты вершины параболы
Парабола, график, вершина, нули.
теория по математике 📈 функции
Функция вида y=ax 2 +bx+c, где а, b, с – некоторые числа, причем, а ≠ 0 число, х – переменная, называется квадратичной функцией.
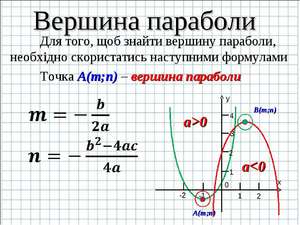
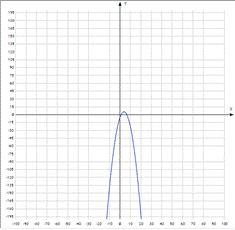
Графиком квадратичной функции является парабола, она имеет вершину и две ветви, которые могут быть направлены либо вверх, либо вниз (рис.1). Красной точкой обозначена вершина параболы, из которой выходят ветви. Её координаты по графику – (3; –4). Направление ветвей зависит от значения коэффициента «а», то есть, если «а» – положительное число, то ветви направлены вверх; если число «а» – отрицательное, то ветви направлены вверх. На данном рисунке ветви направлены вверх, значит коэффициент «а» у формулы, которая задает эту функцию – положительное число. Коэффициент «с» показывает ординату (у) точки пересечения ветви параболы с осью у. Так, на рисунке №1 парабола пересекает ось у в точке (5;0), значит коэффициент с=5.
Чтобы найти координаты вершины параболы (х0; у0), надо воспользоваться формулой:
для нахождения у0 можно просто подставить значение х0 в формулу данной функции y0=ax 2 +bx+c вместо х.
Рассмотрим это на примере конкретно заданной функции.
Пример №1
Найти вершину параболы, заданной формулой у=2х 2 – 8х + 5.
Найдем, чему равны коэффициенты: а=2; b= – 8
Подставим их в формулу и вычислим значение х0:
Теперь в заданную по условию формулу вместо х подставим найденное значение у0=2 ∙ 2 2 – 8 ∙ 2 + 5=8 – 16 + 5= –3
Итак, мы нашли координаты вершины параболы: (2; –3).
Значения х, при которых функция принимает значения, равные нулю, называются нулями функции. Другими словами, Значения абсцисс (х) точек пересечения ветвей параболы с осью х, называются нулями функции. На рисунке №1 точки координаты точек пересечения ветвей параболы с осью х следующие: (1;0) и (5;0). Значит, нули функции – это значения х, равные 1 и 5.
Рассмотрим, как найти нули функции не по рисунку, а по заданной формуле.
Пример №2
Найти нули функции у=х 2 +4х – 5
Так как нули функции это абсциссы точек пересечения ветвей параболы с осью х, то их координаты будут (х;0), то есть у=0. Значит, вместо у подставляем нуль в нашу формулу 0=х 2 +4х – 5 и получаем квадратное уравнение, решив которое, мы и найдем значения нулей функции:
D=b 2 – 4ac=4 2 — 4 ∙ 1 ∙ ( − 5 ) = 36
Значит, нули функции равны –5 и 1
Примечание к заданию по нахождению нулей функции без графика
Если дискриминант уравнения отрицательный, значит, нулей функции нет, то есть парабола не пересекает ось х (вершина находится выше неё, если ветви направлены вверх и ниже, если ветви направлены вниз).
Рассмотрим нахождение соответствия рисунков парабол, расположенных в системе координат значениям а и с.
Пример №3
Для выполнения данного задания на соответствие необходимо сначала поработать с графиками, подписав на них, какими – отрицательными или положительными являются коэффициенты а и с.
Теперь можно выполнить соответствие:
Пример №4
Рассмотрим еще пример на соответствие
В данном задании рассмотрим коэффициенты в формулах и подчеркнем их: так, в формуле под буквой А коэффициент а=-2, т.е. отрицательный, значит, ветви направлены вниз, а это график под номером 2. В формулах под буквами Б и В первые и третьи коэффициенты одинаковые, значит, сравнить по рисунку их невозможно, следовательно, будем сравнивать по расположению вершины (справа или слева от оси у), а именно х0.
Итак, найдем х0 для формулы «Б»:
Видим, что х0 отрицательное, значит, вершина расположена слева от оси у, а это рисунок 3. Ну и осталось привести в соответствие В и 1.
А) a>0, с >0 Б) а 0 В) а>0, с
На рисунках в задании изображены параболы. Вспомним, что обозначают коэффициенты а и с: а – направление ветвей (a 0 – ветви вверх); коэффициент с показывает ординату точку пересечения параболы с осью х (с >0 – пересечение в положительном направлении; с 0, с >0 — это график №1
Б) а 0 — это график №3
pазбирался: Даниил Романович | обсудить разбор | оценить
Установите соответствие между функциями и их графиками.
ФУНКЦИИ
Сразу обратим внимание на вариант В. Эта функция единственная, имеющая положительный коэффициент при х 2 (здесь а=1, т.е. а>0). При а>0 график параболы направлен ветками вверх. Такой график имеется только один – под №3. Кроме того, можно обратить внимание на коэфициент с. Она равен 3, т.е. с>0. Это указывает на то, что парабола должна пересечь ось Оу выше начала координат. Что и отображено на графике В. Получаем соответствие: В–3.
Оба других графика – 1-й и 2-й – пересекают ось Оу ниже начала координат, что соответствует значению с=–3
pазбирался: Даниил Романович | обсудить разбор | оценить
На рисунках изображены графики функций вида
Установите соответствие между знаками коэффициентов a и c и графиками функций.
Мы вспоминаем, за что отвечают коэффициенты a и b при построении графиков функции вида
Коэффициент a определяет направление ветвей параболы: если a > 0, то ветви направлены вверх, а если a 0.
Далее мы смотрим, на что влияет коэффициент c.
Коэффициент c отвечает за положение параболы относительно оси x, или же отвечает за сдвиг по оси y, а именно:
если c > 0, то вершина параболы расположена выше оси х
Из всего вышеперечисленного можно найти ответ:
pазбирался: Даниил Романович | обсудить разбор | оценить
Квадратичная функция. Построение параболы
8 класс, 9 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные понятия
Функция — это зависимость «y» от «x», при которой «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.
Задать функцию означает определить правило в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
График функции — это объединение всех точек, когда вместо «x» можно подставить в функцию произвольные значения и найти координаты этих точек.
Еще быстрее разобраться в теме и научиться строить график квадратичной функции можно на курсах по математике в онлайн-школе Skysmart.
Построение квадратичной функции
Квадратичная функция задается формулой y = ax 2 + bx + c, где x и y — переменные, a, b, c — заданные числа, обязательное условие — a ≠ 0. В уравнении существует следующее распределение:
График квадратичной функции — парабола, которая имеет следующий вид для y = x 2 :
Если в уравнении квадратичной функции старший коэффициент равен единице, то график имеет ту же форму, как y = x 2 при любых значениях остальных коэффициентов.
График функции y = –x 2 выглядит, как перевернутая парабола:
Зафиксируем координаты базовых точек в таблице:
Посмотрев на оба графика можно заметить их симметричность относительно оси ОХ. Отметим важные выводы:
Рассмотрим три случая:
Если a > 0, то график выглядит как-то так:
0″ height=»671″ src=»https://lh6.googleusercontent.com/8ryBuyxmK9S2EbnsNc4AE5PEl_NpIg0RAM_Y_V8wUP-zREEHNgi9QoQTl8FXxoujjWRAvf3s-MPRsXsoepaLLSTHDX-ReGtrsnLQp4dW3WaEyPF2ywjVpYFXlDIpAEHoIiwlxiB7″ width=»602″>
На основе вышеизложенного ясно, что зная направление ветвей параболы и знак дискриминанта, у нас есть понимание, как будет выглядеть график конкретной функции.
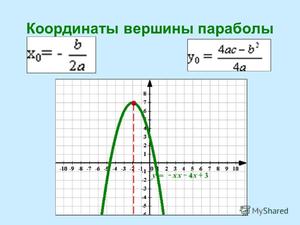
Координаты вершины параболы также являются важным параметром графика квадратичной функции и находятся следующим способом:
Ось симметрии параболы — прямая, которая проходит через вершину параболы параллельно оси OY.
Чтобы построить график, нам нужна точка пересечения параболы с осью OY. Так как абсцисса каждой точки оси OY равна нулю, чтобы найти точку пересечения параболы y = ax 2 + bx + c с осью OY, нужно в уравнение вместо х подставить ноль: y(0) = c. То есть координаты этой точки будут соответствовать: (0; c).
На изображении отмечены основные параметры графика квадратичной функции:
Алгоритм построения параболы
Рассмотрим несколько способов построения квадратичной параболы. Наиболее удобный способ можно выбрать в соответствии с тем, как задана квадратичная функция.
Уравнение квадратичной функции имеет вид y = ax 2 + bx + c.
Как строим:
В данном случае дискриминант больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ. Чтобы найти их координаты, решим уравнение:
Как строим:
Уравнение квадратичной функции имеет вид y = (x + a) × (x + b)
Рассмотрим следующий пример: y = (x − 2) × (x + 1).
Как строим:
Данный вид уравнения позволяет быстро найти нули функции:
(x − 2) × (x + 1) = 0, отсюда х₁ = 2, х₂ = −1.
Определим координаты вершины параболы:
Найти точку пересечения с осью OY:
с = ab = (−2) × (1) = −2 и ей симметричная.
Отметим эти точки на координатной плоскости и соединим плавной прямой.
Как найти вершину параболы: три формулы
Парабола присутствует в мире математики, физики и других наук. По траектории параболы передвигаются искусственные спутники, которые стремятся покинуть пределы Солнечной системы, мяч при игре в волейбол тоже описывает её траекторию. Нужно уметь строить параболу. А чтобы это не составляло труда, надо знать, как найти вершину параболы.
Нахождение вершины параболы: способы, примеры, советы
У каждой точки параболы есть симметричная ей, кроме одной точки, и эта точка называется вершиной. Для того чтобы найти точку, которая является вершиной, нужно определиться, что такое точка на графике. Точка на графике – это определённая координата по оси абсцисс и по оси ординат. Она обозначается как (x; y). Давайте разбираться, как найти заветные числа.
Первый способ
Например, y =x 2 –8 x +15;
находим первый, второй коэффициенты и свободный член;
подставляем значения a и b в формулу;
вычисляем значения y;
Значит, вершина находится в точке (4;-1).
Рассмотрим на примере y =x 2 –6x+5
1) Приравниваем к нулю:
2) Находим дискриминант, используя формулу: D = b 2 –4 ac:
3) Находим корни уравнения по формуле (-b±√ D)/2a:
Второй способ
Дополнение до полного квадрата – отличный способ узнать, где располагается вершина. Используя этот способ, вы сможете вычислить точки x и y одновременно, без нужды подставлять x в начальный пример. Рассмотрим этот метод на примере функции: y=x 2 +8 x +10.
2. Теперь в левой части нужно сделать полный квадрат. Для этого посчитайте (b/2) 2 и увеличьте обе части уравнения результат. В этом случае нужно подставит 8 вместо b.
У нас получается 16. Теперь прибавьте это число к обеим частям уравнения:
3. Видно, что полученное выражение – полный квадрат. Его можно представить в форме: (x + 4) 2 = 6.
4. Используйте это выражение для поиска координат вершины параболы. Чтобы посчитать x, нужно приравнять его к 0. Получаем, x =-4. Координата y равна тому, что находится в правой части, то есть y =6. Вершина параболы этого уравнения (-4, 6).
Третий способ
Если вы знаете, что такое производная, то для вас есть другая формула. Несмотря на то, куда смотрят «рога» параболы, её вершина — точка экстремума. Для этого способа надо применить следующий алгоритм:
1. Нахождение первой производной по формуле f'(x) = (ax² + bx + c)’ = 2ax + b.
2. Приравнивание производной к 0. В итоге вы получите 0 = 2ax + b, отсюда можно найти то, что нас интересует.
Рассмотрим этот способ подробнее.
Дана функция y = 4x²+16x-17;
f'(x) = (4x²+16x-17)’ = 8x+16 =0
Построение параболы
Самое трудное при построении – это верно найти точки функции. Для подробного построения нужно просчитать 5–7 точек (для школьного курса хватит этого). Для этого выбираем какое-либо значение x и подставляем его в данную функцию. Итогом подсчётов будет число точки по оси ординат. После этого ставим на координатную плоскость полученные нами точки. В итоге у нас получается парабола.
2) Заполняем таблицу
Так как парабола имеет осевую симметрию, то можно считать только значения справа или слева от вершины. Лучше считать те значения, которые ближе к 0, так удобнее. В нашем случае эти значения 4 и 5.
| X | 4 | 5 | 5,5 | 6 | 7 |
| Y | -4 | -6 | -6,25 | -6 | -4 |
Советы
Правильно находите коэффициенты.
Пишите промежуточные вычисления на бумаге. Это не только облегчит нахождение вершины, но и поможет найти свои ошибки.
Делайте всё поэтапно. Следуйте алгоритму.
Обратите ваше внимание на то, что:
Видео
Это видео поможет вам научиться находить вершину параболы
Уравнение по трем точкам: как найти вершину параболы, формула
Многие технические, экономические и социальные вопросы прогнозируются при помощи кривых. Наиболее используемым типом среди них является парабола, а точнее, ее половина. Важной составляющей любой параболической кривой является ее вершина, определение точных координат которой иногда играет ключевую роль не только в самом отображении протекания процесса, но и для последующих выводов. О том, как найти ее точные координаты, и пойдет речь в данной статье….
Начало поиска
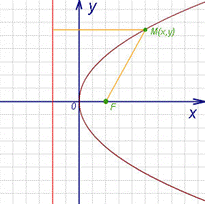
Перед тем как перейти к поиску координат вершины параболы, ознакомимся с самим определением и его свойствами. В классическом понимании параболой называется такое расположение точек, которые удалены на одинаковом расстоянии от конкретной точки (фокус, точка F), а также от прямой, которая не проходит через точку F. Рассмотрим данное определение более предметно на рисунке 1.
Рисунок 1. Классический вид параболы
На рисунке изображена классическая форма. Фокусом является точка F. Директрисой в данном случае будет считаться прямая параллельная оси Y (выделена красным цветом). Из определения можно удостовериться, что абсолютно любая точка кривой, не считая фокуса, имеет себе подобную с другой стороны, удаленную на таком же расстояние от оси симметрии, как и сама. Более того, расстояние от любой из точек на параболе равно расстоянию до директрисы. Забегая вперед, скажем, что центр функции не обязательно должен находиться в начале координат, а ветки могут быть направлены в разные стороны.
Парабола, как и любая другая функция, имеет свою запись в виде формулы:
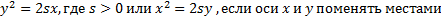
В указанной формуле буква «s» обозначает параметр параболы, которая равна расстоянию от фокуса до директрисы. Также есть и другая форма записи, указано ГМТ, имеющая вид:
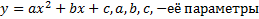
Такая формула используется при решении задач из области математического анализа и применяется чаще, чем традиционная (в силу удобства). В дальнейшем будем ориентироваться на вторую запись.
Это интересно! Первый признак равенства треугольников: доказательство
Расчет коэффициентов и основных точек параболы
К числу основных параметров принято относить расположение вершины на оси абсцисс, координаты вершины на оси ординат, параметр директрисы.
Численное значение координаты вершины на оси абсцисс
Если уравнение параболы задано в классическом виде (1), то значение абсциссы в искомой точке будет равняться половине значения параметра s (половине расстояния между директрисой и фокусом). В случае, если функция представлена в виде (2), то x нулевое рассчитывается по формуле:
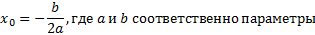
Т.е., глядя на эту формулу, можно утверждать, что вершина будет находиться в правой половине относительно оси y в том случае, если один из параметров a или b будет меньше нуля.
Уравнение директрисы определяется следующим уравнением:
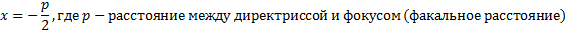
Это интересно! Что такое деление с остатком: примеры для ребенка в 3, 4 классе
Значение вершины на оси ординат
Численное значение местонахождения вершины для формулы (2) на оси ординат можно найти по такой формуле:
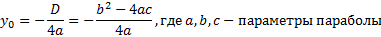
Отсюда можно сделать вывод, что в случае если а<,0, то вершина кривой будет находиться в верхней полуплоскости, в противном случае – в нижней. При этом точки параболы будут обладать теми же свойствами, что были упомянуты ранее.
Если дана классическая форма записи, то более рациональным будет вычисление значения расположения вершины на оси абсцисс, а через него и последующее значение ординаты. Отметим, что для формы записи (2), ось симметрии параболы, в классическом представлении, будет совпадать с осью ординат.
Важно! При решении заданий с использованием уравнения параболы прежде всего выделите основные значения, которые уже известны. Более того, нелишним будет, если будут определены недостающие параметры. Такой подход заранее даст большее «пространство для маневра» и более рациональное решение. На практике старайтесь использовать запись (2). Она более проста для восприятия (не придется «переворачивать координаты Декарта), к тому же подавляющее количество заданий приспособлено именно под такую форму записи.
Это интересно! Чему равна и как найти площадь равностороннего треугольника
Построение кривой параболического типа
Используя распространенную форму записи, перед тем как построить параболу, требуется найти ее вершину. Проще говоря, необходимо выполнить следующий алгоритм:
Т.е. алгоритм не представляет собой ничего сложного, основной акцент делается на том, как найти вершину параболы. Дальнейший процесс построения можно считать механическим.
При условии, что даны три точки, координаты которых известны, прежде всего необходимо составить уравнение самой параболы, а потом повторить порядок действий, который был описан ранее. Т.к. в уравнении (2) присутствуют 3 коэффициента, то, используя координаты точек, вычислим каждое из них:
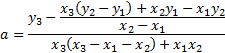
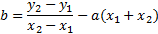
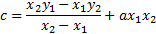
В формулах (5.1), (5.2), (5.3) применяются соответственно тех точек, которые известны (к примеру А ( 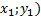
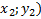
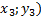
При построении параболы всегда должна присутствовать ось симметрии. Формула оси симметрии для записи (2) будет иметь такой вид:
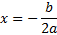
Т.е. найти ось симметрии, которой симметричны все точки кривой, не составляет труда. Точнее, она равна первой координате вершины.
Это интересно! Изучаем математику в игровой форме: как ребенку быстро выучить таблицу умножения
Наглядные примеры
Пример 1. Допустим, имеем уравнение параболы:
Требуется найти координаты вершины параболы, а также проверить, принадлежит ли точка D (10, 5) данной кривой.
Решение: Прежде всего проверим принадлежность упомянутой точки самой кривой
Откуда делаем вывод, что указанная точка не принадлежит заданной кривой. Найдем координаты вершины параболы. Из формул (4) и (5) получаем такую последовательность:
Пример 2. Найти вершину параболы, зная три точки, которые ей принадлежат: A (2,3), B (3,5), C (6,2). Используя формулы (5.1), (5.2), (5.3), найдем коэффициенты уравнения параболы. Получим следующее:
Используя полученные значения, получим следующие уравнение:
На рисунке заданная функция будет выглядеть следующим образом (рисунок 2):
Рисунок 2. График параболы, проходящий через 3 точки
Т.е. график параболы, который проходит по трем заданным точкам, будет иметь вершину в 1-й четверти. Однако ветки данной кривой направлены вниз, т.е. имеется смещение параболы от начала координат. Такое построение можно было предвидеть, обратив внимание на коэффициенты a, b, c.
В частности, если a<,0, то ветки» будут направлены вниз. При a>,1 кривая будет растянута, а если меньше 1 – сжата.
Константа c отвечает за «движение» кривой вдоль оси ординат. Если c>,0, то парабола «ползет» вверх, в противном случае – вниз. Относительно коэффициента b, то определить степень влияния можно лишь изменив форму записи уравнения, приведя ее к следующему виду:
Если коэффициент b>,0, то координаты вершины параболы будут смещены вправо на b единиц, если меньше – то на b единиц влево.
Важно! Использование приемов определения смещения параболы на координатной плоскости подчас помогает экономить время при решении задач либо узнать о возможном пересечении параболы с другой кривой еще до построения. Обычно смотрят только на коэффициент a, так как именно он дает четкий ответ на поставленный вопрос.
Полезное видео: как найти вершину параболы
Полезное видео: как легко составить уравнение параболы из графика
Вывод
Такой как алгебраический процесс, как определение вершин параболы, не является сложным, но при этом достаточно трудоемкий. На практике стараются использовать именно вторую форму записи с целью облегчения понимания графического решения и решения в целом. Поэтому настоятельно рекомендуем использовать именно такой подход, и если не помнить формулы координаты вершины, то хотя бы иметь шпаргалку.