Как научить пользоваться транспортиром ребенка
Класс: 5
Презентация к уроку
I. Организационный момент
II. Вступительное слово учителя
Мы познакомимся с измерительным прибором (как он называется, вы узнаете немного позже), научимся с его помощью измерять, а затем и строить углы. Вы покажите свои знания, докажите насколько внимательны.
Будем учиться не только математике, но и умению общаться, уважению друг к другу.
Для того чтобы достичь наших целей, вы должны быть волевыми, настойчивыми, целеустремленными, поэтому эпиграфом нашего урока будут слова:
III. Устная работа
Какие из углов, изображенных на рисунке, являются:
а) острыми;
б) тупыми;
в) есть ли среди этих углов прямые?
О каком угле мы с вами еще не вспомнили? [О развернутом]
Какой угол называется развернутым? Острым? Прямым? Тупым?
Мы знаем, что два угла можно сравнивать друг с другом.
Какой способ для этого мы использовали? [Наложение]
Но углы, также как и отрезки, можно сравнивать не только наложением, но и с помощью измерения.
IV. Изучение нового материала
Для построения и измерения углов используют специальный прибор. Как он называется, вы узнаете, отгадав кроссворд.
1. Результат деления.
2. Лучи образующие угол.
3. Точка, из которой выходят лучи образующие угол.
4. Угол, который образуют два дополнительных друг другу луча.
5. Результат сложения.
6. Угол, который составляет половину развернутого угла.
7. Инструмент, который используют для построения прямого угла.
8. Угол, меньше прямого.
9. Угол, больше прямого, но меньше развернутого.
10. Результат умножения.
11. Результат вычитания.
Учитель демонстрирует учащимся транспортир или показывает на плакате:
– Для измерения углов применяют транспортир. Положите перед собой транспортиры. Вы видите, какие они разные, но у всех есть нечто общее, о чем мы сейчас будем говорить.
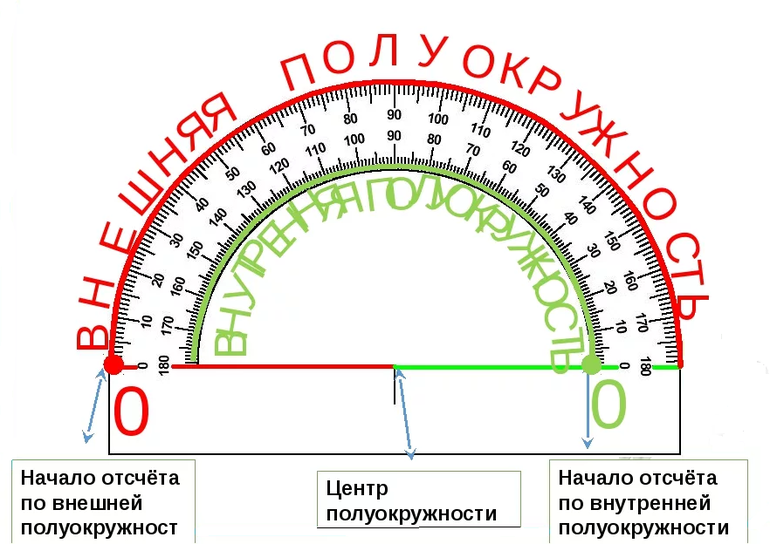
Слайд 5. Итак, шкала транспортира. Она расположена на полуокружности и пронумерована
от 0 до 180. Бывают шкалы двойные: нумерация идет слева направо и справа налево.
Слайд 6. Также есть круглые транспортиры, шкала идет по кругу от 0 до 360, но она также разделена на две полуокружности.
Центр этой полуокружности отмечен на транспортире точкой или черточкой. Найдите на своем транспортире центр и покажите его.
Штрихи шкалы транспортира делят полуокружность на 180 равных частей. Лучи, проведенные из центра полуокружности через эти штрихи, образуют 180 углов, каждый из которых равен 
Слайд 7. Итак, градусом называют 
Историческая справка
Слово «градус» – латинское, означает «шаг», «ступень». Измерение углов в градусах появилось более 3 тыс. лет назад в Вавилоне. В расчетах там использовались шестидесятеричная система счисления, шестидесятеричные дроби.
С этим связано, что вавилонские математики и астрономы, а вслед за ними греческие и индийские, полный оборот (окружность) делили на 360 частей – градусов (шесть раз по шестьдесят), каждый градус – на 60 минут, а минуту – на 60 секунд:
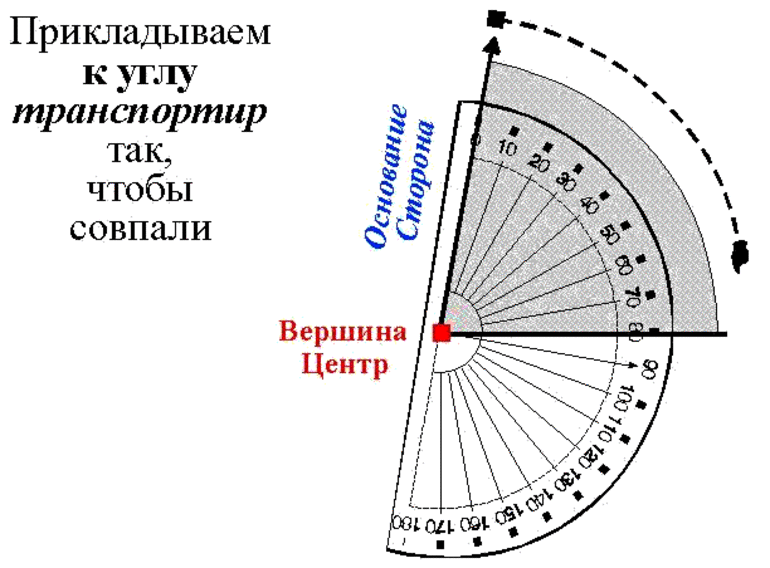
Объяснение учителя (с демонстрацией на доске), как с помощью транспортира можно измерить угол.
– Как измеряют углы с помощью транспортира?
1) Нужно вершину угла совместить с центром транспортира.
2) Одна сторона угла должна проходить через нулевую отметку (0° по шкале).
3) Вторая сторона угла должна пересекать шкалу. Нужно посмотреть, через какую
отметку проходит вторая сторона угла. Это и есть величина этого угла.
Если у транспортира есть две шкалы, то надо смотреть на отметку той шкалы, через ноль которой проходит одна из сторон угла.
V. Практическая работа
Каждому ученику выдается набор углов: острый, прямой, тупой и развернутый.
а) развернутого угла;
б) прямого угла;
в) острого угла;
г) тупого угла.
Вывод:
| – развернутый угол равен 180°; – прямой угол равен 90° (половина развернутого угла); – острый угол меньше 90°; – тупой угол больше 90°, но меньше 180°. |
Задание: Начертите в тетради угол любой величины. Предложите соседу по парте его измерить.
VII. Работа по карточкам
У всех учеников карточки с одинаковым заданием.
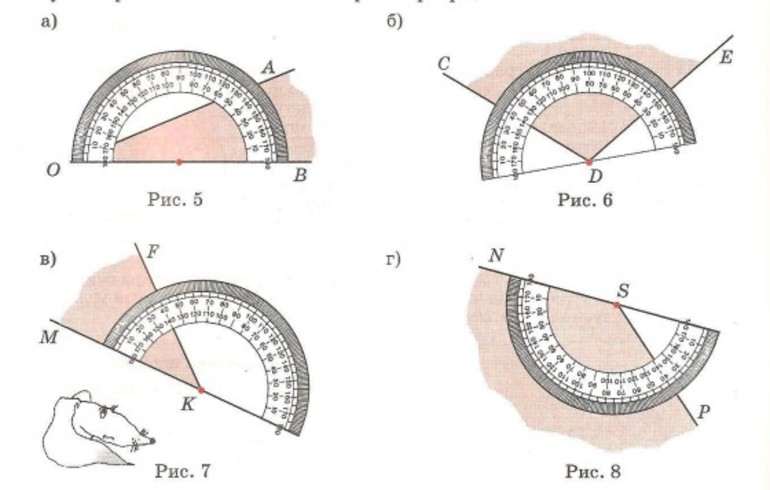
Задание: Измерьте углы и запишите результаты измерений в тетрадях.
Задание: Выполняется устно с использованием модели часов.
Какой угол образуют часовая и минутная стрелки часов:
а) в 3 ч; в) в 10 ч; д) в 2 ч 30 мин;
б) в 5 ч; г) в 6 ч; е) в 5 ч 30 мин?
Задача №1652
Луч ОС лежит внутри угла АОВ, причем 

Конспект урока «Измерение углов. Транспортир»
Саракташский районный отдел образования
Муниципальное общеобразовательное бюджетное учреждение
«Черкасская средняя общеобразовательная школа имени Чумакова Г.Т»
Урок математики. 5 класс
Измерение углов. Транспортир.
Дедловский Юрий Анатольевич,
высшая квалификационная категория,
педагогический стаж 35 лет
На данном уроке дети повторно знакомятся с таким чертёжным инструментом как транспортир
Объект исследования – углы. Дети вспоминают части транспортира, учатся находить значение величины угла, отрабатывают алгоритм пользования транспортиром, учатся классифицировать виды углов по величине – прямые, острые, тупые.
На уроке предполагается работа в группах по 3-4 человека.
Дети учатся использовать приобретённые знания и навыки при выполнении практических работ.
познакомить учащихся с единицей измерения углов, с прибором для измерения углов;
научить пользоваться транспортиром.
развивать внимание, мышление учащихся;
развивать самостоятельность учащихся, используя проблемные ситуации, творческие задания;
развивать познавательный интерес к предмету.
воспитывать чувство взаимоуважения;
воспитывать у учащихся навыки учебного труда.
4.Формировать универсальные учебные действия:
коммуникативные (умение принимать ответственное решение при совместной деятельности в микрогруппе, построение речевых высказываний, согласованность действий с партнёрами, планирование учебного сотрудничества),
личностные (умение соблюдать установленные правила),
регулятивные (самоконтроль, самооценка, целеполагание, планирование, прогнозирование, умение формулировать тему и выявлять объект исследования, коррекция),
познавательные (умения классифицировать, ставить проблему, выделять существенное, наблюдать, обобщать, строить речевые высказывания, делать выводы и использовать полученные знания в практической деятельности).
ПК, проекционное оборудование, презентация к уроку;
Чертёжные инструменты (треугольники, линейки, транспортиры);
Деятельность учащихся на уроке
Формирование УУД на каждом этапе урока
Задача: создать условия для возникновения у учеников внутренней потребности включения в учебный процесс.
Дети приветствуют учителя. Рассаживаются за столы, которые расставлены для работы в группе (5 групп по 3 – 4 человека)
Занимай свои места.
Чтоб от безделья не зевать
Полезно голову ломать!
Регулятивные (самоконтроль, организация учебного места)
Задача: создать условия для возникновения внутренней потребности включения в учебную деятельность, вызвать интерес.
Для измерения длины, времени, массы.
У детей получается отчёт. Самопроверка.
Дети выбирают руководителей групп, специалистов, определяют их обязанности, вспоминают правила работы в группах.
Руководитель будет обобщать высказывания детей, контролировать действия членов своей группы.
ПРАВИЛА РАБОТЫ В ГРУППАХ
-прислушиваемся к мнению товарищей
— высказываемся по очереди
-доверяем руководителю озвучить решение группы.
У каждой группы на столе лежит коробка с различными предметами. Среди них полоска бумаги.
Нам понадобится линейка. Дети измеряют полоску бумаги.
Учитель предлагает рассмотреть линейку, весы, часы. Для чего нужны эти предметы? Что они измеряют?
Предлагаю поработать в группах. Для этого нужно распределить обязанности и выбрать руководителя. Какие обязанности будет выполнять руководитель? Чем занимаются остальные?
Вспомним правила работы в группе.
Каким чертёжным инструментом вы воспользуетесь, чтобы измерить полоску бумаги? Какая мерка вам нужна?
Познавательные УУД (умение классифицировать, извлечение из памяти сохранённой информации)
Коммуникативные УУД (построение речевых высказываний, аргументация своего мнения)
(определение и понимание учебной задачи)
Актуализация и постановка проблемы.
Задача: актуализация знаний, достаточных для построения нового знания, фиксация учащихся затруднений в выполнении.
Угол – фигура, состоящая из двух лучей, берущих начало в одной точке.
У детей на столах два угла. Измеряют при помощи треугольника, линейки – знакомых чертёжных инструментов.
Дети в группах совещаются и ищут свои способы доказательства. Высказывают предположения. Дают разные ответы. Возможно проверить способом наложения углов. Возможно какая – нибудь группа догадается взять ножницы, вырезать углы и наложить их друг на друга.
Ответы детей. Возможно кто-нибудь вспомнит транспортир.
Отгадывают и получают ключевое слово «транспортир»
Найдите изображения углов. Вспомните, какая фигура называется угол?
Теперь измеряем углы, которые лежат в ваших конвертах: красный и синий. Какой больше? Как догадались?
Сравните углы и начертите в тетради точно такие же. Каким инструментом вы пользовались, чтобы начертить больший угол?
Посмотрите на доску, я не начертил эту фигуру, т.к. очень сложно начертить при помощи треугольника и линейки угол. Докажите, что у вас получились именно такие же углы.
А вы знаете, что существует специальный чертёжный инструмент для измерения и построения углов? Знаете как он называется?
Учитель предлагает отгадать при помощи кроссворда название этого нового для учащихся чертёжного инструмента.
1. Результат деления.
2. Лучи образующие угол.
3. Точка, из которой выходят лучи образующие угол.
4. Угол, который образуют два дополнительных друг другу луча.
5. Результат сложения.
6. Угол, который составляет половину развернутого угла.
7. Инструмент, который используют для построения прямого угла.
8. Угол, меньше прямого.
9. Угол, больше прямого, но меньше развернутого.
10. Результат умножения.
11. Результат вычитания.
Регулятивные УУД (планирование, прогнозирование, определение и понимание учебной задачи)
Познавательные УУД (постановка проблемы)
Личностные УУД (выражение своих мыслей, познавательная мотивация)
Построение проекта выхода из проблемной ситуации.
Задача: сформулировать и согласовать тему и цели урока, построить план достижения цели.
Тема урока: Измерение углов с помощью транспортира. Цель урока: Научиться пользоваться транспортиром при измерении и построении углов. Объекты исследования: различные углы.
Дети самостоятельно формулируют тему урока, называют объект исследования, формулируют цель урока
В каждой группе текст.
Когда же появился транспортир? Оказывается, эта угловая мера возникла много тысяч лет назад. Предполагают, что это было связано с созданием первого календаря. Древние математики нарисовали круг и разделили его на столько же частей, сколько дней в году. Но они думали, что в году не 365 или 366 дней, а 360 дней. Поэтому круг разделили на 360 равных частей. Такое изображение было очень удобным, на нём можно было отмечать каждый прошедший день, и видеть, сколько дней осталось до конца года. Каждой части дали название – градус. Градусная мера сохранилась и до наших дней
Слово «градус» – латинское, означает «шаг», «ступень». Измерение углов в градусах появилось более 3 тыс. лет назад в Вавилоне. В расчетах там использовались шестидесятеричная система счисления, шестидесятеричные дроби.
С этим связано, что вавилонские математики и астрономы, а вслед за ними греческие и индийские, полный оборот (окружность) делили на 360 частей – градусов (шесть раз по шестьдесят), каждый градус – на 60 минут, а минуту – на 60 секунд:
Почему древние математики разделили круг на 360 равных частей?
Когда возник этот прибор?
Какое название получила каждая часть?
Есть шкала и центр. Полукруглая шкала разделена на 180 частей или градусов.
Дети по-разному прикладывают транспортир. В каждой группе получаются разные результаты.
Руководители групп подходят к доске и записывают величину углов.
Сформулируйте тему сегодняшнего урока.
Что будет объектом исследования?
Перед началом работы определим учебную задачу.
Познакомимся с историей возникновения транспортира.
Беседа по содержанию.
Придумайте вопросы по содержанию.
А теперь давайте подробнее рассмотрим транспортиры.
Рассмотрите транспортиры. В чём они схожи?

ОСНОВНАЯ ЛИНИЯ ТРАНСПОРТИРА.)
Итак, в руках у вас прибор для измерения углов. Приложите транспортир и определите величину углов, лежащих у вас на столе.
Коммуникативные УУД (согласованность действий с партнёрами)
Личностные УУД (умение соблюдать установленные правила)
Умение работать с текстовой информацией.
Умение анализировать текст, ставить вопросы по содержанию, поиск необходимой информации
Открытие новых знаний.
Задача: выбор учащимися метода разрешения проблемной ситуации и на основе выбранного метода выдвижение и проверка гипотез.
Мы не умеем ими пользоваться.
Нужно создать алгоритм измерения углов при помощи транспортира.
АЛГОРИТМ ИЗМЕРЕНИЯ УГЛОВ ТРАНСПОРТИРОМ
1.Совместим вершину угла с центром транспортира
2.Расположить транспортир так что бы при этом одна из сторон совпала с основной линией транспортира (то есть совместить с 0 )
3. Найти штрих на шкале, через который проходит вторая сторона.
4. Определить градусную меру угла, учитывая его вид.
Дети правильно прикладывают транспортиры и записывают данные на листах бумаги. Руководители групп выходят и показывают наработки групп.
Не у всех получились одинаковые результаты.
Что-то делаем неправильно.
Есть на транспортире две шкалы с делениями: внешняя и внутренняя.
Дети затрудняются ответить. Нужно понаблюдать.
Вывод: Если угол острый, то смотрим значение по внутренней стороне, а если тупой, то по внешней стороне
Давайте сравним полученные результаты. Транспортиры у всех одинаковые, а результаты получились разные. В чём проблема?
Как решить проблему?
Но сначала немножко отдохнём.
Покажите руками угол 0, 90°, 180°, 360.
Покажите руками острый угол, тупой угол.
Покажите рукой, где вокруг нас есть прямые углы.
Повернитесь на 180°. А теперь на 90°, а теперь на 360.
Пользуясь алгоритмом (он лежит перед детьми) определите величину углов на вашем столе.
Какой вывод можно сделать?
Почему результаты получились разные. На что нужно обратить внимание? Посмотрите внимательно на транспортир. Что вы заметили?
По какой шкале нужно смотреть значение измерений?
Обратимся к последнему пункту алгоритма.
ПРОВЕРЬТЕСООТВЕТСТВУЕТ ЛИ ПОЛУЧЕННАЯ МЕРА УГЛА ЕГО ВИДУ(ТУПОЙ, ПРЯМОЙ,ОСТРЫЙ)
Сделайте вывод: какой угол можно считать острым, а какой тупым?
Личностные УУД (определение своей роли в группе, стремление к эффективной работе, осознание ответственности за общее дело, эмпатия по отношению к другим)
Познавательные УУД (выстраивание логической цепи рассуждений, формулирование выводов, анализ, синтез, сравнение, обобщение, выдвижение гипотез и их обоснование, установление причинно – следственных связей, создание алгоритма действий
Коммуникативные УУД (умение договариваться, учёт разных мнений)
Задача: Применить полученные знания в практических действиях.
Острые – 35, 80, 63, 45
Тупые – 135, 170, 92, 112
Чертят углы и проверяют задание у одноклассников.
Детям предлагаются величина углов – нужно определить острый угол или тупой?
135, 35, 80, 170, 63, 92, 45, 112
Начертите в тетради каждый индивидуально один острый и один тупой угол. Значения углов подпишите. Обменяйтесь тетрадями в группе и проверьте.
О каком угле мы с вами еще не вспомнили? [О развернутом и полном]
Какой угол называется развернутым, полным? Острым? Прямым? Тупым?
Мы знаем, что два угла можно сравнивать друг с другом.
Какой способ для этого мы использовали? [Наложение]
Регулятивные УУД (контроль, коррекция, оценка)
Познавательные УУД (выполнение действий по алгоритму)
Коммуникативные УУД (формулирование и аргументация своего мнения)
Самостоятельная работа с самопроверкой по эталону.
Задача: самостоятельное выполнение учащимися заданий, самопроверка, сравнение с алгоритмом.
Задание: Выполняется устно с использованием модели часов.
Какой угол образуют часовая и минутная стрелки часов:
а) в 3 ч; в) в 10 ч; д) в 2 ч 30 мин;
б) в 5 ч; г) в 6 ч; е) в 5 ч 30 мин?
Личностные УУД (адекватное понимание причин успешности или неуспешности)
Познавательные УУД (выполнение действий по алгоритму)
(мобилизация сил для преодоления препятствий, распределение времени)
Задача: Организовать самооценку учениками деятельности на уроке.
Измерение углов с помощью нового чертёжного инструмента – транспортира.
Мы учились измерять углы с помощью транспортира. Научились отличать острый угол от тупого по его величине.
Дети записывают свои ответы.
Вспомним о теме нашего урока.
Какую цель мы перед собой ставили?
Как вы считаете достигли ли мы её?
У каждого из вас есть листок, на котором написано
Личностные УУД (самооценка по критериям успешности, адекватное оценивание себя)
Начертить в тетради с помощью транспортира пять острых углов, пять тупых углов, прямой угол. Значения величин углов подписать
Люди обычно сталкиваются с транспортирами в математике, когда учатся в школе создавать точные геометрические фигуры. Возможно, у многих из них никогда больше не будет причин снова использовать эти приборы, тем не менее транспортиры имеют долгую историю применения в различных областях.
История изобретения
Происхождение этого математического инструмента восходит к жрецам в Египте и Вавилоне, которые установили меру углов в градусах, минутах и секундах. Однако до времён классической Греции тригонометрия не использовалась в математике.
Во втором веке до нашей эры астроном Гиппарх из Никии изобрёл тригонометрический стол, для измерения треугольников. Затем Птолемей включил в свою великую астрономическую книгу «Альмагест» таблицу, с угловыми приращениями от 0 до 180°, с погрешностью менее 1/3600 единиц. Он также объяснил метод составления этой таблицы, и на протяжении всей книги приводил много примеров того, как вычислять с помощью неё неизвестные элементы фигур.
Птолемей также был автором, так называемой теоремы Менелая для решения сферических треугольников, и на протяжении многих веков его тригонометрия была основным пособием для астрономов.
Возможно, в то же время, учёные Индии также разработали тригонометрическую систему, основанную на функции синуса, которая, в отличие от используемого в настоящее время синуса, была не пропорцией, а длиной стороны, противоположной углу в прямом треугольнике этой гипотенузы. Индийские математики использовали разные значения для этого в своих таблицах.
Томас Бландевиль рассказал о приборе специально созданном, для рисования и измерения фигур в своём «Кратком описании универсальных карт» 1589 года. Как видно из названия, он применял его, чтобы править навигационные карты для использования в высоких широтах.
Другие европейские математики также описывали подобные приборы примерно в то же время. Независимо от того, кто первым придумал этот инструмент, к началу XVII века он вошёл в стандартную практику мореплавателей и геодезистов. К XVIII веку транспортиры начали появляться в учебниках по геодезии и геометрии.
Транспортиры в современном понимании возникли во второй половине XVIII века, когда такие учёные, как Джесси Рамсден и Георг Фридрих Брандер, усовершенствовали ранее созданные устройства.
В то время предпочтительными материалами для их изготовления были:
В первой половине XX века начали применять олово и целлулоид.
Называться транспортиром (рус.) прибор стал в 1610 году. Термин произошёл от средневекового слова protractor, что означает «переносить», который, в свою очередь, произошел от латинского слова protrahere «тянуть вперёд».
Разновидности и использование
Транспортир — это простой гониометр для измерения или создания угла. Он выглядит как круглый или полукруглый диск с делением. Диск может быть изготовлен из пластика, прочной бумаги или листового металла. Типичными являются диаметры от 8 до 15 см и деления на 1° и 0,5°, при измерении также 0,5 Гон (новый градус). Точность составляет от 0,1 до 0,5° в зависимости от диаметра шкалы. Более точные приборы имеют поворотную рейку со шкалой (длина до миллиметра).
Частично из-за различного использования их изготавливают во многих формах: знакомый полукруг, а также круги, прямоугольники, квадраты или четверть круга (квадранты). Они также могут иметь различные диаметры. Их изготавливают из латуни, стали, дерева, слоновой кости или пластика. Самой распространённой формой является полукруг с ограничительной шкалой в 180 градусов.
Угловой транспортир — градуированный круглый инструмент с одной поворотной рукой; используется для измерения или разметки. В строительстве часто требуется отмерить угол в 90 градусов. Иногда прилагается шкала Вернье, чтобы дать более точные показания. Прибор широко применяется для изготовления архитектурных и механических чертежей, хотя его использование уменьшилось с появлением современного программного обеспечения для рисования.
Универсальные транспортиры скоса используются изготовителями инструментов; поскольку они делают измерения посредством механического контакта с предметом, то классифицируются как механические транспортиры.
Угловой транспортир применяется для того, чтобы измерить и проверить углы с очень жёсткими допусками. Он считывает до 5 угловых минут (5 или 1/12°) и может измерять от 0 до 360°.
Сегодня также применяются электронные приборы, которые обычно работают с поворотным датчиком. Кроме того, связанными с транспортиром приборами являются:
Измерение градусов угла
Для того чтобы научиться пользоваться транспортиром инструкция нужна на начальном этапе. Для его освоения достаточно нескольких минут и примеров (смотреть онлайн) того, как можно измерить и построить угол с помощью этого прибора.
Измерить угол, значит найти его величину. Углы разделяют на три типа: острый, тупой и прямой. Прямоугольный имеет 90 градусов. Все углы что имеют больше этого значения называются тупыми, и соответственно меньше 90 градусов называются острыми. Развёрнутый угол имеет 180 градусов.
Понимание того, что углы являются частями окружностей, полезно, потому что тогда конструкция транспортира обретает смысл. Поскольку полный круг имеет 360º, отдельный угол должен быть меньше этого числа, потому что он часть круга.
Алгоритм измерения следующий: для того чтобы измерить угол транспортиром необходимо приложить его центр верхней кромки линейки к вершине измеряемого угла. Вершина — это точка, в которой две из трёх сторон треугольника пересекаются.
Нижнюю планку (основание) транспортира нужно выставить горизонтально. Каждый транспортир имеет точку, спроектированную в центре основания, Эта средняя точка располагается на вершине угла, который должен быть измерен или нанесён на график. Другая сторона должна пересекать транспортир в одной из точек его дуги.
Если вторая сторона (линия) до дуги не доходит нужно продолжить её с помощью простой или масштабной линейки. То число, на шкале дуги, которое будет пересечено линией и есть величина угла в градусах.
Для удобства на большинстве транспортиров сделано две шкалы, внутренняя и внешняя, которые отображают числа в каждой строке.
Построение угла
Берётся чистый лист бумаги в клетку. На нём карандашом отмечается точка, от которой проводиться прямая линия, как одна из сторон будущего угла. Эта черта служит для того, чтобы задать направление второй стороне. В простых упражнениях, для приобретения навыка построения угла, линия проводится горизонтально.
Центр основы транспортира располагается на любом из концов черты, который будет вершиной угла. Эта точка отмечается на бумаге карандашом. И именно к этому месту, внутри отверстия и присоединяется вершина угла, одна из сторон которого должна совпадать в горизонтальной плоскости с внутренней стороной линейки транспортира.
Затем на шкале отмечается необходимый градус. С внутренней стороны отверстия также обозначается точка возле этого градуса. И от вершины проводится прямая линия к этой точке. Таким образом, получается необходимый угол.
Для того чтобы правильно пользоваться транспортиром очень важно его выровнять, и точно прикладывать, для получения верных измерений.
Пересечённые линии в верхней части прямой кромки линейки должны совпадать с вершиной (конечной точкой), где соединяются два луча.