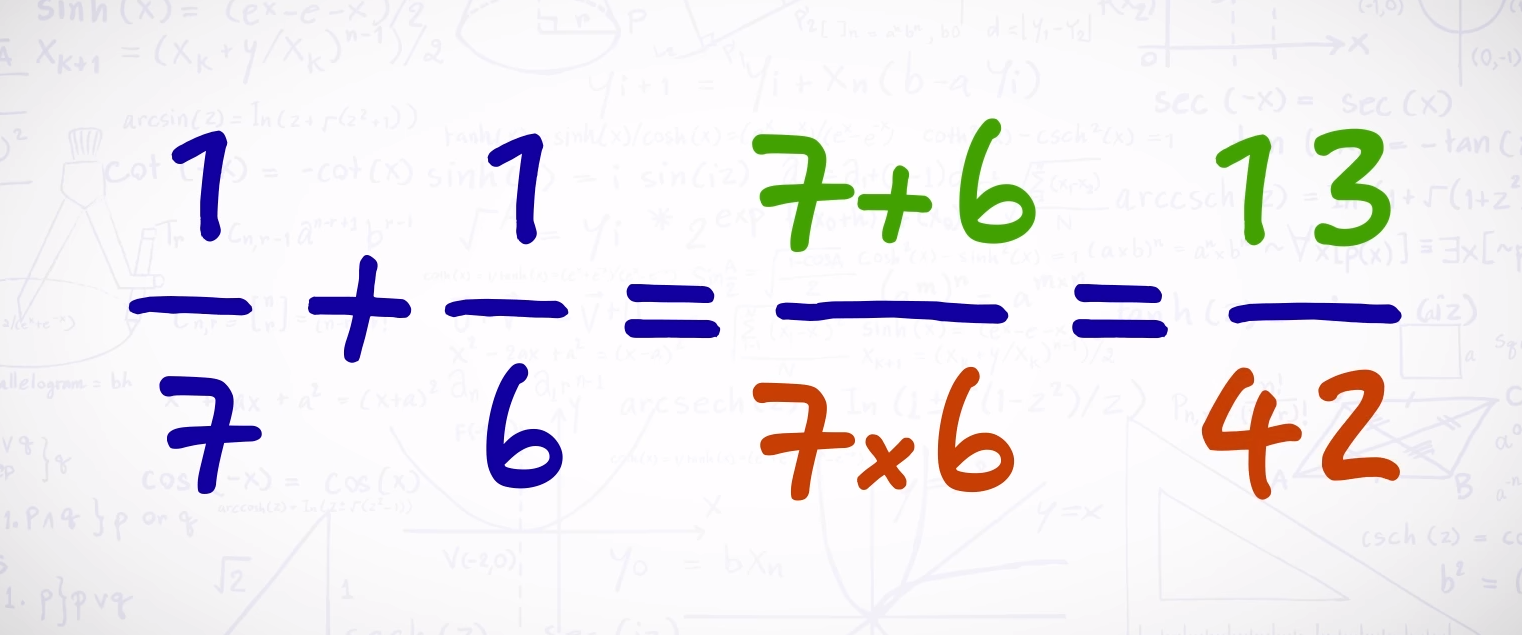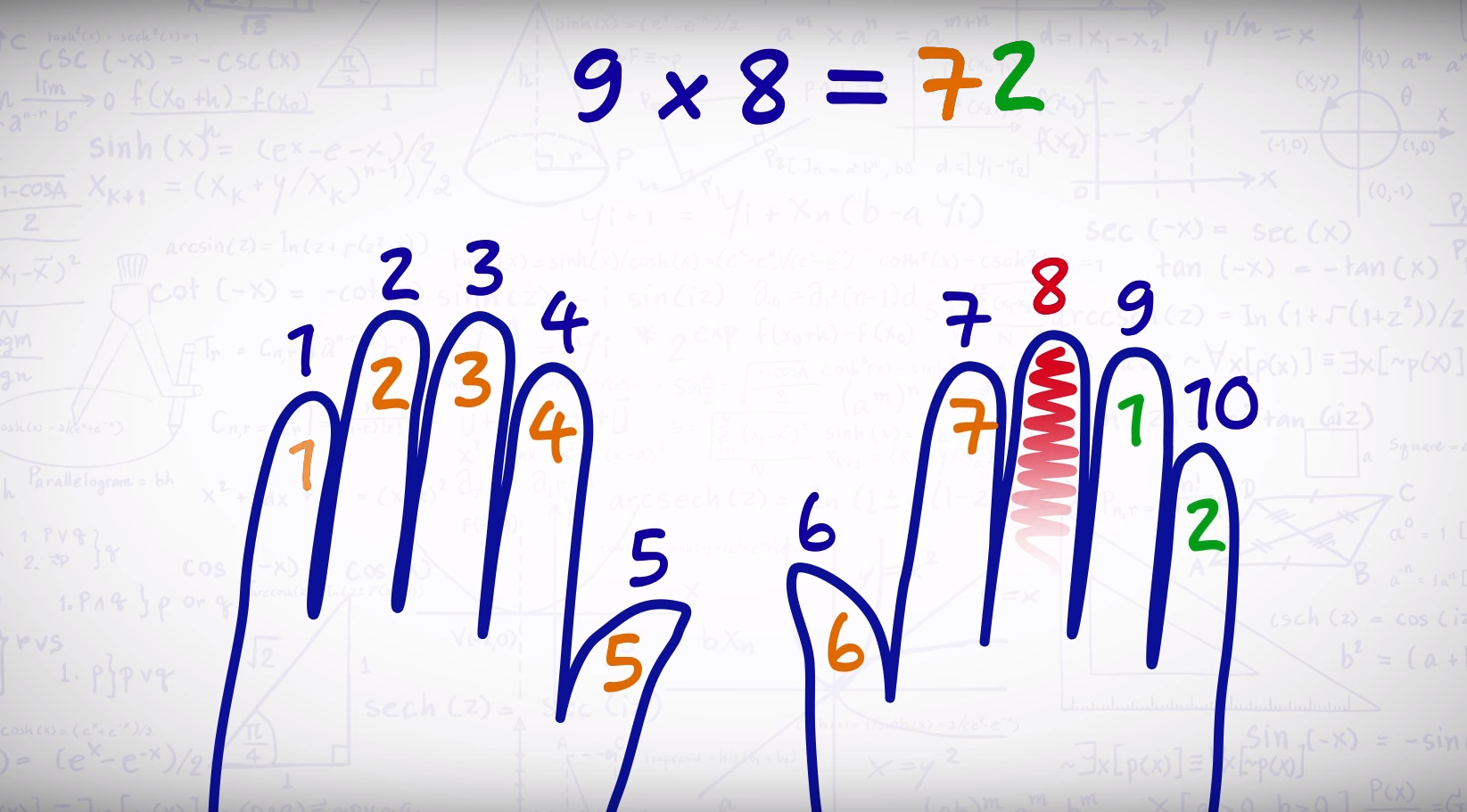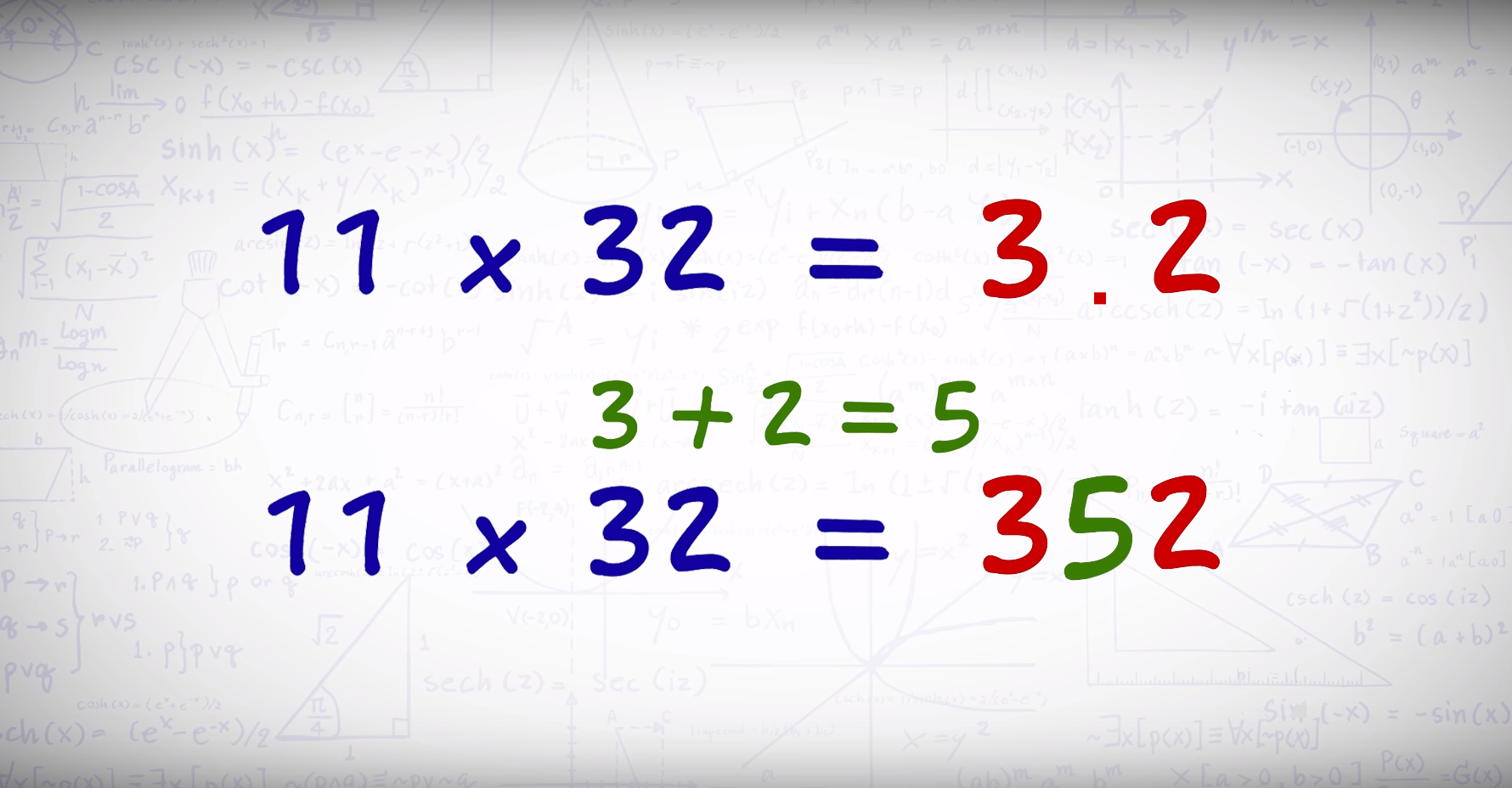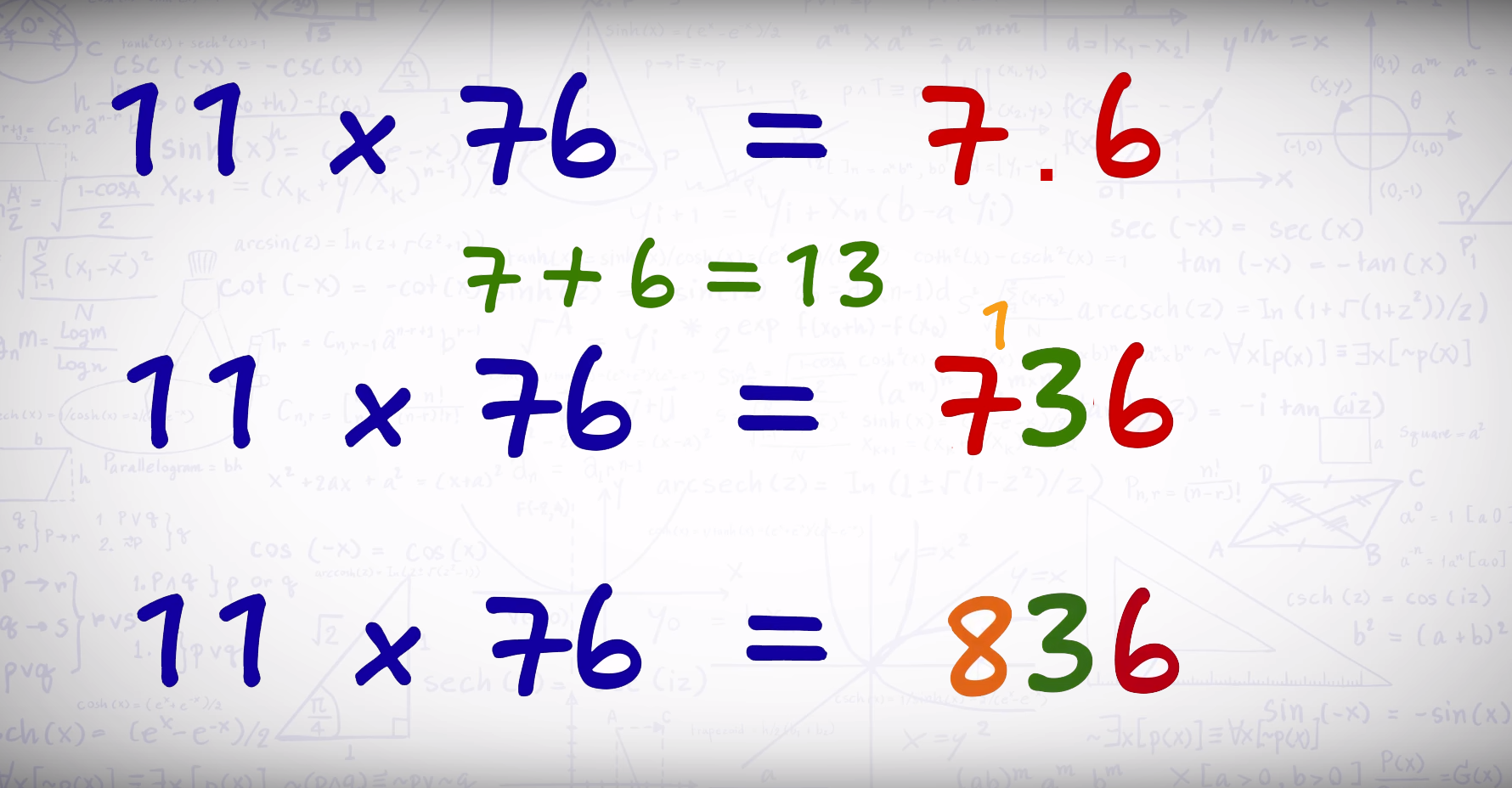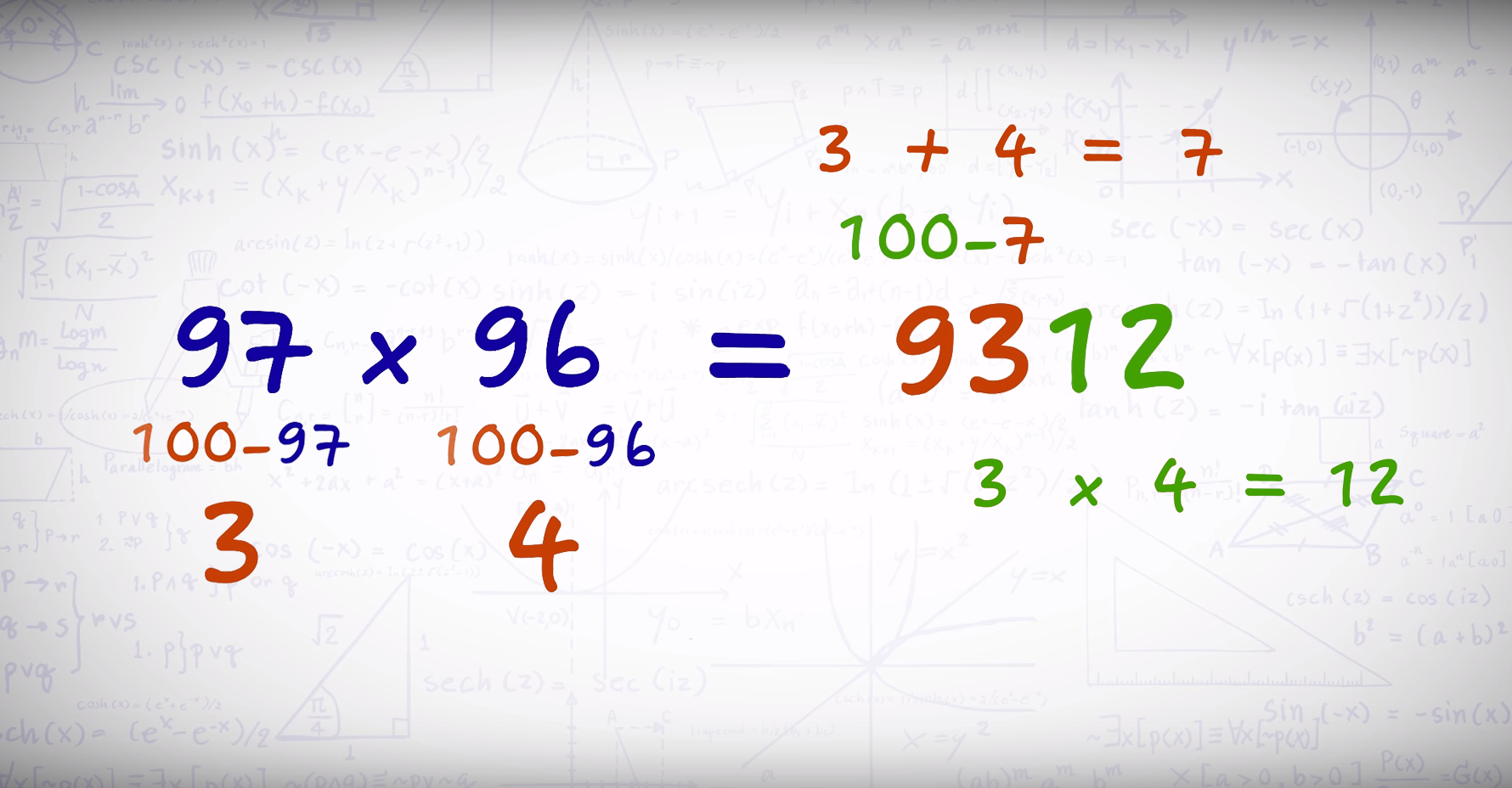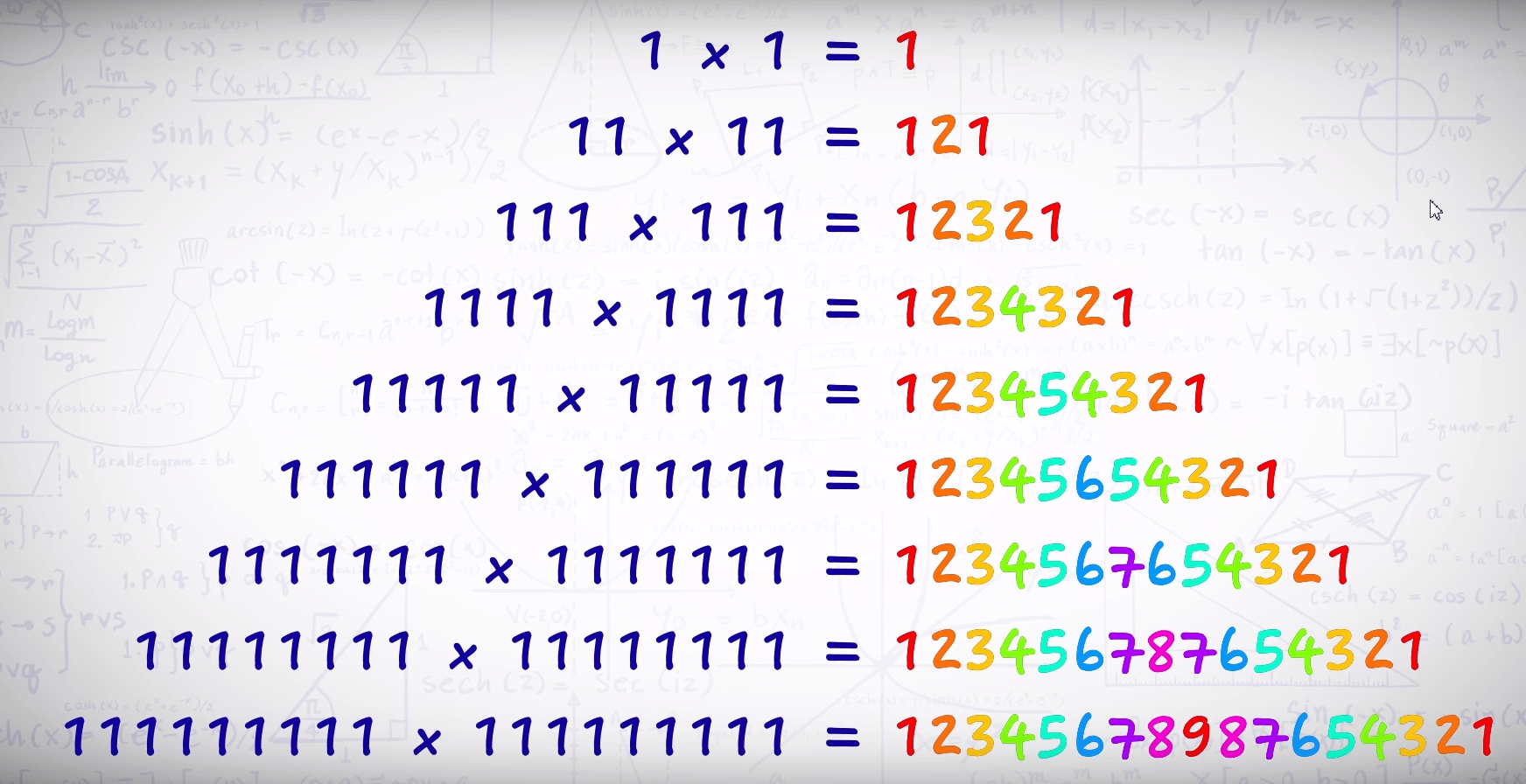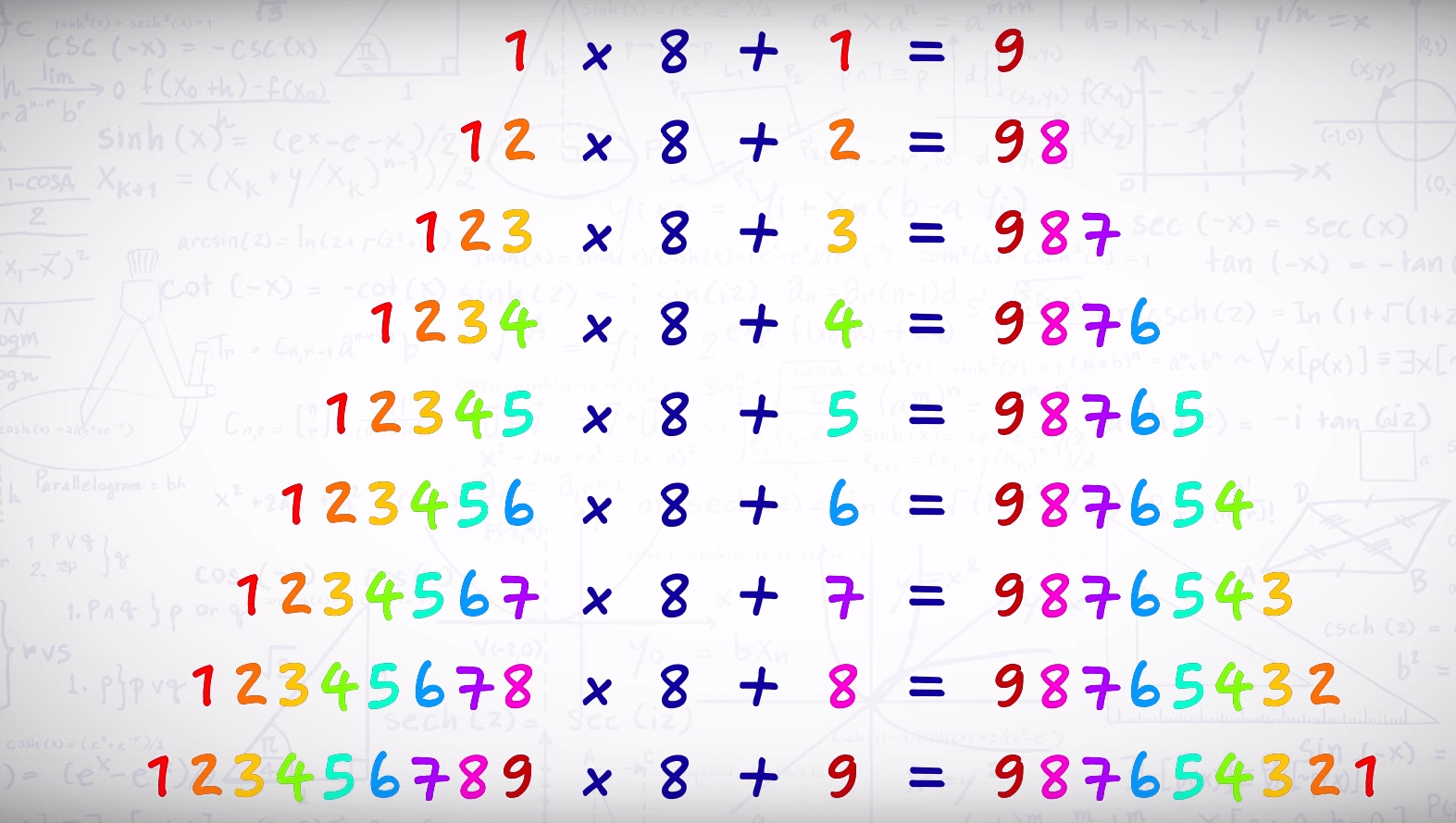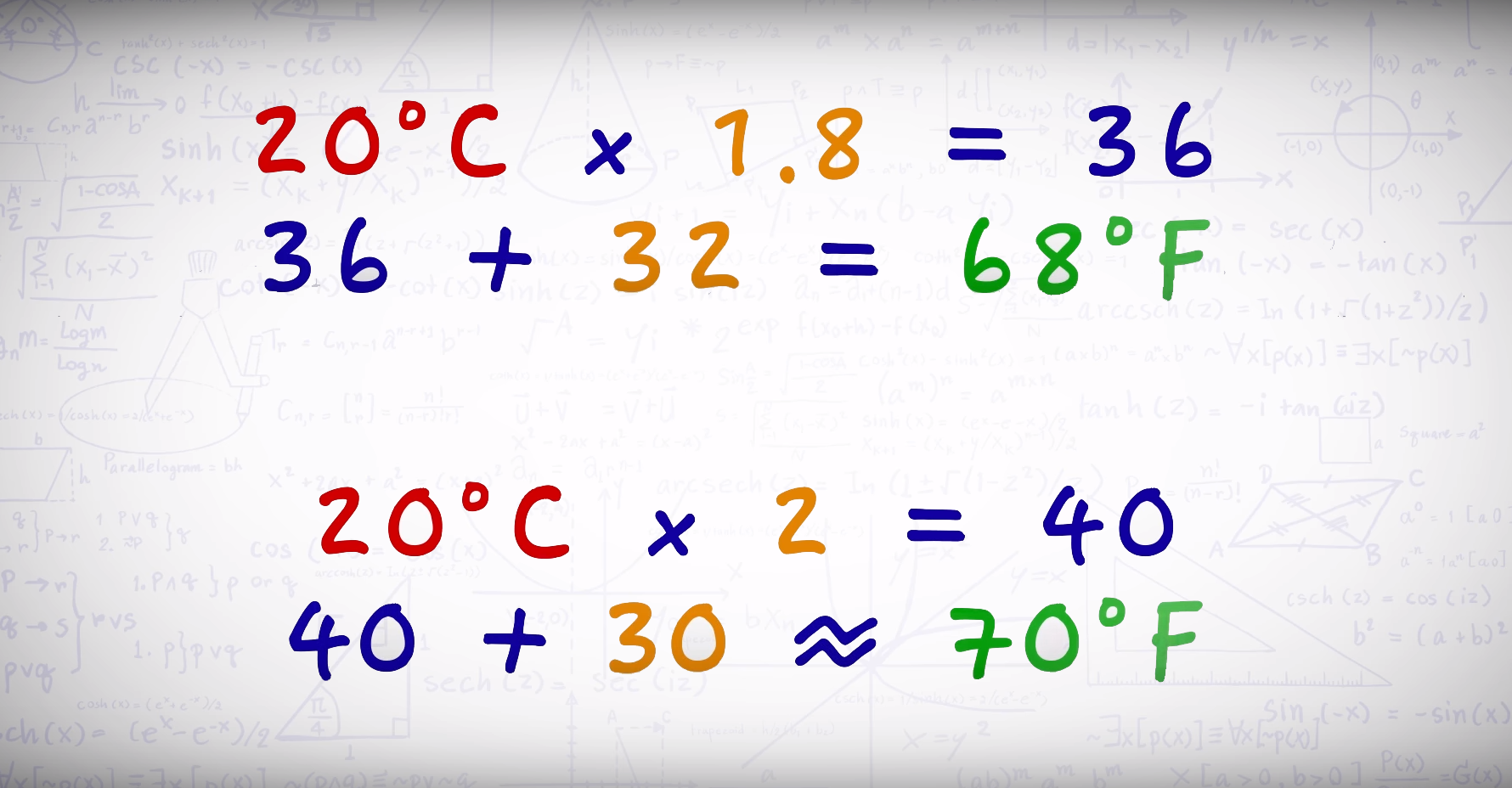Как научиться считать на пальцах
Умножение и сложение на пальцах рук: 3 забытых русских способа, которые вас удивят
Вы когда-нибудь задумывались почему дети, когда учатся считать, делают это на пальцах? Оказывается, это сложилось исторически очень и очень давно.
Единственной причиной, заставившей большинство народов избрать десятичную систему счисления, является то, что у человека на руках десять пальцев. Счёт на пальцах широко применялся в древнем мире и средневековье. Об исторической роли напоминают и языковые факты.
В «Арифметике» Магницкого числа 1, 2, 3, …9 называются «перстами», ноль называется «низачто», полные десятки — «составами», числа, состоящие из десятков и единиц — «сочинители». Эти названия являются аналогами таких же названий в европейских языках.
Впервые у Герберта (французский учёный монах-математик, 940 — 1003; с 999 г. Римский папа Сильвест II) встречаются для чисел в пределе сотни: digiti — пальцевые числа 1, 2, …9 (digitus — палец), articuli — суставные числа, полные десятки, compositi — составные из десятков и единиц.
Итальянский математик Леонардо Пизанский (наиболее известен под прозвищем Фибоначчи, дата рождения — ок. 1170 г.) и авторы, знакомые с арабской арифметикой, употребляли терминологию: unitates — единицы, deceni — десятки; авторы эпохи Возрождения — употребляли греческие слова monadici (единицы), decades(десятки). Термин «десятичная, или декадная система счисления» начинает широко употребляться с конца XVIII в.
Пальцевой счёт был необходим в торговых местах, где сталкивались представители разных народов, не имевших общего языка. Практическая необходимость выработала общий пальцевой счёт, и ему даже обучали в школах.
Старинный русский способ умножения чисел от 6 до 9 (таблица умножения до 5 заучивалась) применялся купцами как вспомогательный при устном счёте. Если нужно было перемножить два числа a и b, которые оба больше 5 и меньше 9, то:
Чтобы было понятно — разберём на примере:
Найти произведение чисел 7 и 9.
Сожмём пальцы рук в кулаки. Число 7 больше 5 на 2, число 9 — на 4. Разогнём на одной руке 2 пальца, на другой —4. Сумма 2 +4 = 6, значит число десятков в искомом произведении 6, остались сжатыми пальцы на руках 3 и 1, перемножаем их: 3× 1 = 3. Это будет число единиц в искомом. Получили 63. Действительно, 7 × 9 = 63.
Интересно, правда? Попробуйте сами, потренируйтесь, умножьте: 6 на 8.
Ещё был известен способ «счёт дюжинами».
Счёт дюжинами (по 12) вёлся большим пальцем по фалангам остальных четырёх пальцев правой руки, начиная от нижней фаланги указательного пальца до верхней фаланги мизинца.
Если число превышало 12, то при достижении 12 считающий загибал палец на другой руке. При достижении пяти дюжин, т.е. 12 × 5 = 60, все пальцы руки были загнуты в кулак.
Дюжинами в России до начала XX века было принято считать пишущие перья, карандаши, наборы из 12 предметов вилок, ложек, комплекты стульев и кресел на 12 персон (помните, роман И.Ильфа и Е.Петрова «Двенадцать стульев»).
А ещё на Руси был распространён «счёт сорокАми».
Охотники за пушным зверем в Сибири считали «сорочками» — укомплектованными в мешками шкурками (как правило, 40 соболиных хвостов и 40 беличьих шкурок, именно столько уходило на пошив шубы (сорочки) русского боярина XVI века). Счёт сороками напоминал счёт дюжинами, только подсчёта фаланг считали суставы пальцев, которых 8 (см. рис.).

Следы пальцевого «счёта сороками» сохранились в народных суевериях: несчастливым для охотника считался сорок первый медведь.
Об исторической роли счёта на пальцах говорят и названия числительных у разных народов: часто число пять называется «рукой», десять — «две руки», двадцать — «весь человек», т.е. 2 руки и 2 ноги.
Ментальная Арифметика на Пальцах

Ответ счета в Ментальной Арифметики может исходить только с объяснением математики пальцев. Если вы посмотрите на этот аккуратный способ подсчета до 99 на ваших двух руках, то вы поймете Соробан — Абакус! Четыре бусинки означают четыре пальца на руке и отдельную бусину для большого пальца это нашу пятерку.
Человеческая рука несет пять пальцев; у двух рук их десять. Несомненно, этот факт отвечает за универсальное принятие десятичной системы.
Дети учатся рассчитывать, считая пальцы в математике, сначала до 5 с одной стороны, а затем до 10 на две руки. Тем не менее, есть простой способ подсчитать до 10 с помощью всего 5 пальцев одной руки и до 100, используя обе руки.
Вот как это сделать:
Сложенный кулак может стоять на 10, если вы не планируете использовать секундную стрелку или 0, если вы это сделаете:
Вторая рука используется таким же образом, но для подсчета в математике 10 секунд:
С фотографиями и скриншотами из онлайн-счетов Soroban мы можем показать эту идею. Он работает лучше всего, если вы считаете. Сначала используйте четыре пальца правой руки для подсчета 1, 2, 3, 4. Это соответствует четырем шарикам в первом ряду Соробана, показанным желтым.
Затем вещи становятся немного более абстрактными. Большой палец — 5, сам по себе, точно так же, как и одинокий желтый шарик. Мы переходим от прямого подсчета к символам или иначе образности:
Вы добавляете пальцы в большой палец, чтобы подсчитать 6, 7, 8, 9. Представьте, что маленький ребенок играет с традиционными играми с пальцами с родителями. Дети могут мгновенно распознавать (сублицировать) количества от 1 до 4, но подсчет западных пальцев проходит до 10 — намного выше диапазона субтитизации. В отличие от подсчета западных пальцев, эта система вводит группы и символы (большой палец — 5), а также добавление, как только вы покидаете диапазон субтитизации. Другими словами, система следит за тем, как работают умы детей.
Что происходит, когда вы достигаете 10? Что-то очень полезное и захватывающее! Вы можете использовать другую руку, которая означает значение нового места — и новый ряд бус на абакусе. Цифры, бусины и пальцы — все вместе, как рука в перчатке.
Это интересно, читайте также:
Вот еще одно отличие этой системы от подсчета ваших 10 пальцев. Вы можете сосчитать весь путь до 99 на ваших двух руках!
И если вы объедините силы с другом, вы можете показать еще большие цифры.
Вот видео, показывающее, как считать весь путь от 1 до 99:
Ментальная Арифметика удивительная наука, которая помогает понимать самую из всех точных наук нашу любимую математику. Изучайте и любите математику, она откроет вам много тайн, которые всегда очевидны и интересны. Ваша Ментальная Арифметика.
Таблица умножения, считаем на пальцах
Большинство детей начинают осваивать счёт при помощи пальцев. Вероятно, именно так и начиналась вся математика, ведь рука самый удобный инструмент для элементарных подсчётов, который «всегда с тобой». Однако мало кто знает, что при помощи пальцев можно не только учиться считать, складывать и вычитать. Этот универсальный «прибор» помогает выполнять и более сложные арифметические действия, к примеру: такие, как умножение.
Существует множество методик, которые позволяют ребёнку достаточно быстро и легко выучить таблицу умножения. Все они в достаточной мере эффективны. Однако некоторые примеры всё равно могут даваться малышу с трудом. Вот тут то и помогает пальчиковый счёт.
Нет ничего страшного, если на первых порах ребёнок будет пользоваться этой методикой, чтобы найти правильный ответ. В конце концов, нужное число запомниться, а значит, цель будет достигнута.
Правда, на пальцах можно подсчитать далеко не все примеры из таблицы умножения, а лишь столбики на 6, 7, 8 и 9. Но и в этом есть плюс: именно эта часть таблицы считается самой сложной для запоминания. Так что пальчики в этой работе могут выступить хорошими помощниками.
Секреты умножения на пальцах
Воспользоваться возможностью вычисления примеров из таблицы умножения на пальцах можно только при наличии определённых знаний и навыков. Во-первых, ребёнок должен свободно владеть сложением, а во-вторых, он уже должен знать таблицу умножения от 1 до 5. В противном случае посчитать что-то при помощи пальцев будет достаточно проблематично.
Умножаем на 2 при помощи пальцев
С этого, собственно, можно начать изучение таблицы умножения. Как известно, умножение на 2 – это прибавление к исходной цифре её же самой. Объяснить это ребёнку можно как раз на пальцах.
Два пальца на одной руке и два на другой – всего 4 пальца (2*2=4), пять пальчиков на одной и пять на другой – всего десять пальцев (5*2=10). Тоже самое можно проделать с одним, тремя и четырьмя пальцами. Правда, на первых пяти примерах освоение таблицы умножения на 2 и заканчивается. Дальше подсчёты вести проблематично из-за отсутствия нужных «инструментов». Однако этого уже достаточно, чтобы ребёнок освоил основной принцип умножения на 2. Если при этом он с лёгкостью складывает в пределах 20, то запомнить остальные примеры ему труда не составит.
Умножаем на 9 при помощи пальцев
Изучив таблицу умножения первых пяти столбиков можно нарушить порядок и перескочить сразу на столбец с цифрой 9. Это обусловлено сразу несколькими причинами. Во-первых, в этом столбике очень много закономерностей, которые значительно упрощают запоминание. Во-вторых, эти примеры легче всего посчитать именно на пальцах.
Начнём с закономерностей. Главная из них заключает в том, что сумма цифр всех произведений этого столбика равняется 9, а количество десятков отличаются в меньшую сторону от умножаемого числа на единицу. Для примера можно рассмотреть выражение 5*9. Количество десятков в произведении равно 5-1=4, а количество единиц – 9-4=5. Итого: 45.
Кроме того, рассматривая столбик можно заметить, что количество десятков в каждом следующем ответе увеличивается на единицу, а количество единиц на неё же уменьшается: 09, 18, 27, 36, 45, 54, 63, 72, 81, 90. Кстати, именно на этой закономерности и основан принцип подсчёта примеров из этого столбика на пальцах.
Для этого надо поставить кисти рук ладошками к себе и пронумеровать пальчики цифрами от 1 до 10. Чтобы узнать результат примера нужно загнуть палец с соответствующей цифрой и подсчитать пальчики слева и справа от него. Слева будет количество десятков, а справа – единиц. Например: выражение 5*9. Загнуть надо мизинец на левой руке. Слева останется 4 пальчика, а справа – 5. Ответ: 45.
Умножаем на 6, 7 и 8 при помощи пальцев
Считать на пальцах результаты таблицы умножения на 6, 7 и 8 несколько сложнее, чем производить расчёты, в которых цифры умножаются на 9. Кроме того, посчитать примеры с умножением от 1 до 5 на пальцах не получится. Однако ничего страшного в этом нет. Ведь на этом этапе ребёнок уже более или менее знает таблицу умножения на 1, 2, 3, 4 и 5. Также он понимает главный закон умножения – коммуникативный или переместительный, который гласит, что от перемены мест множителей произведение не изменяется, например: 9*5=45 и 5*9=45. Получается что половину столбиков с умножением на 6, 7 и 8 ребёнком уже выучена. Ну а результаты остальных примеров как раз можно посчитать и на пальцах.
Итак, всё что нужно для такого расчёта, так это две ладошки. Их надо поставить перед собой пальцами друг к другу и пронумеровать пальцы снизу вверх цифрами от 6 до 10, т.е. мизинцы будут обозначены цифрой 6, безымянные пальчики – 7, средние – 8, указательные – 9 и большие 10.
Теперь можно приступать непосредственно к расчётам примеров из таблицы умножения на 6, 7 и 8. Чтобы это сделать надо соединить кончики пальцев с соответствующими цифрами и подсчитать количество пальчиков над соединёнными отдельно на правой и левой руке. Полученные цифры надо перемножить. Получится количество единиц в ответе на соответствующее выражение. Теперь надо посчитать соединённые пальчики и те, которые остались под ними. Это будут десятки. Объединив полученные цифры, получаем итоговый результат умножения.
Сложно и запутано? Это только на первый взгляд. На самом деле всё очень просто. Особенно если рассмотреть все эти действия на конкретном примере.
Итак, чтобы ответить на вопрос «Сколько будет 6*7?», нужно соединить кончик мизинца левой руки с безымянным пальчиком правой. Теперь следует подсчитать. Над соединёнными пальцами на левой руке осталось 4 пальчика, а на правой – 3. Значит количество единиц в произведении равно 4*3=12. Теперь следует узнать количество десятков. Это два соединённых пальца и один под ними, т.е. 3 десятка. Осталось всё суммировать: 30+12=42. Это действительно несложно.
Со всеми остальными примерами из таблицы умножения на 6, 7 и 8 будет ещё проще, поскольку в них не придётся перескакивать через десяток, т.е. количество единиц и десятков будет соответствовать тем цифрам, которые присутствуют в нужном ответе.
Вместо заключения
Счёт на пальцах может и не самый лучший метод для запоминания таблицы умножения. Часто дети хитрят и используют его, чтобы не вспоминать правильный ответ. Однако ругать ребёнка за это не стоит. В итоге он всё равно запомнит все примеры, пусть даже и таким нестандартным способом. Кстати, процесс запоминания пройдёт значительно быстрее, если таблицу умножения постоянно повторят, используя какие-нибудь примеры из жизни.
Видео: «Таблица умножения на пальцах»
В уме и на пальцах: 7 простых математических трюков
Сколько цифр числа Пи вы помните? Можете умножить 97 на 96 в уме? Мы подобрали несколько мнемонических приемов и математических трюков.
Операции с дробями
Сложить две дроби, у которых в числителе стоит единица, очень просто: нужно найти сумму знаменателей и поделить на их произведение:
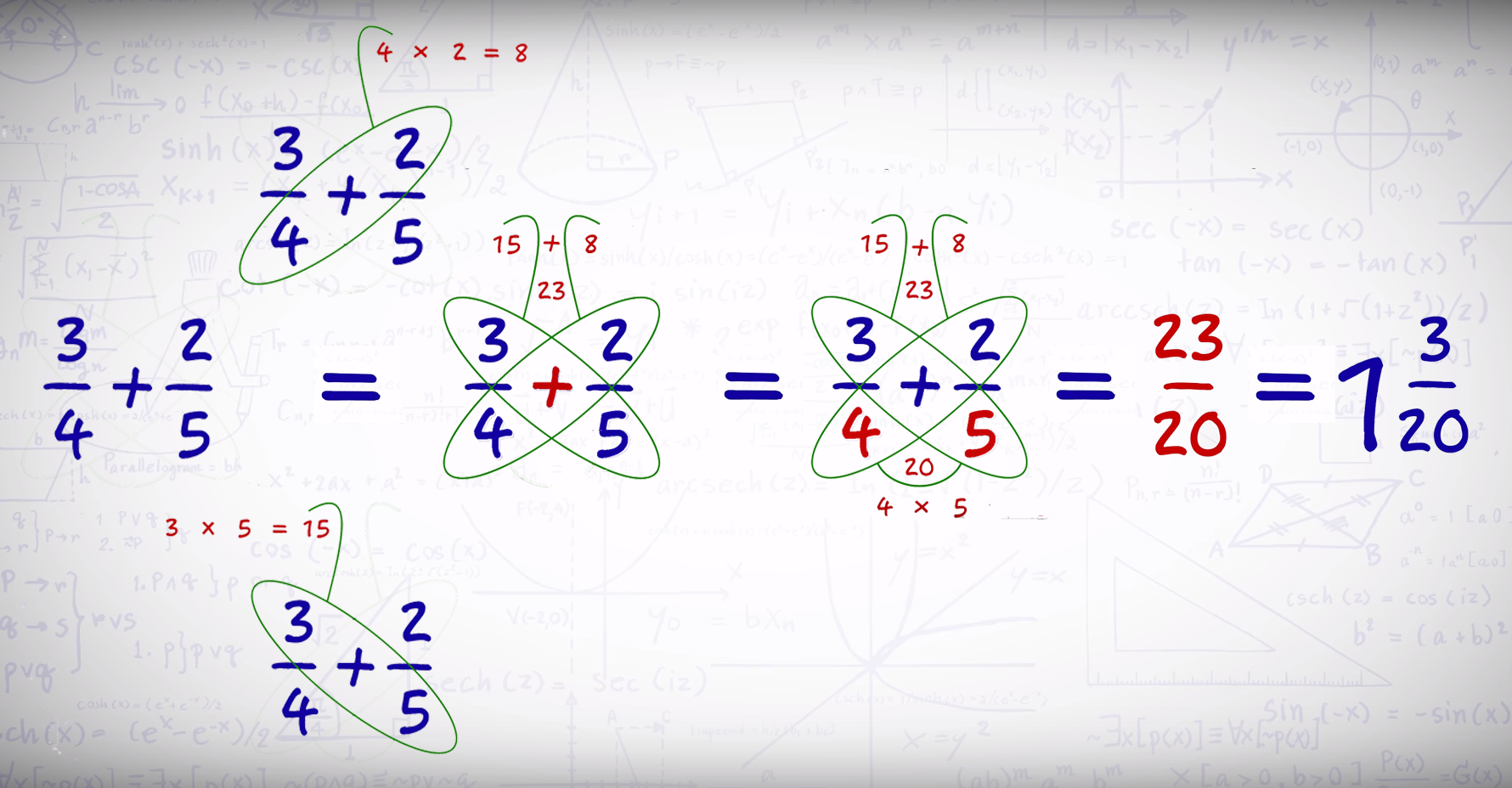
Для более сложных случаев существует метод бабочки. Попробуем с его помощью сложить ¾ и ⅖.
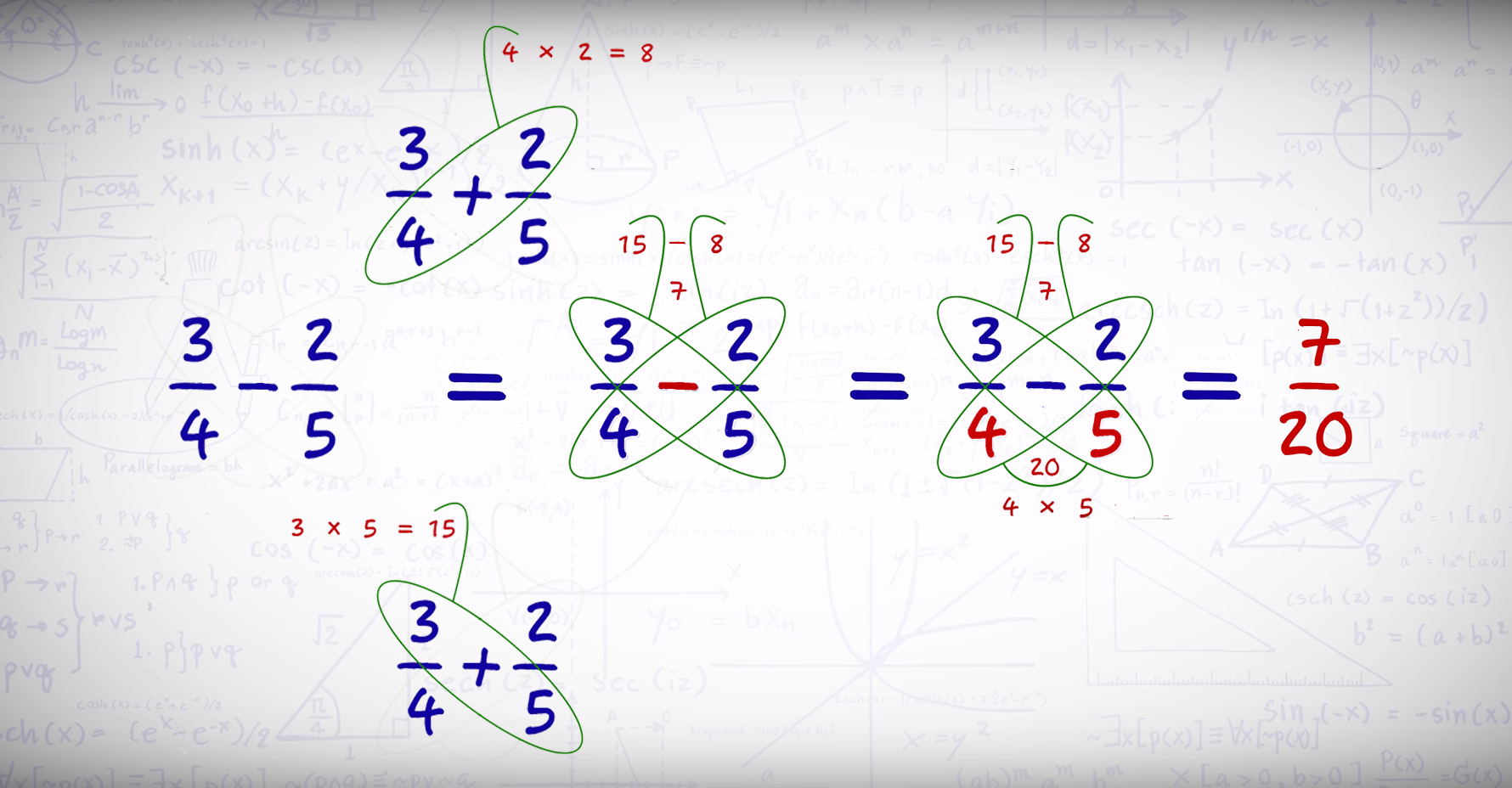
Вычитание осуществляется точно так же, только на втором шаге нужно найти не сумму, а разность двух значений.
Пара математических трюков для умножения на 9
Запомнить таблицу умножения на 9 очень просто: она симметричная.
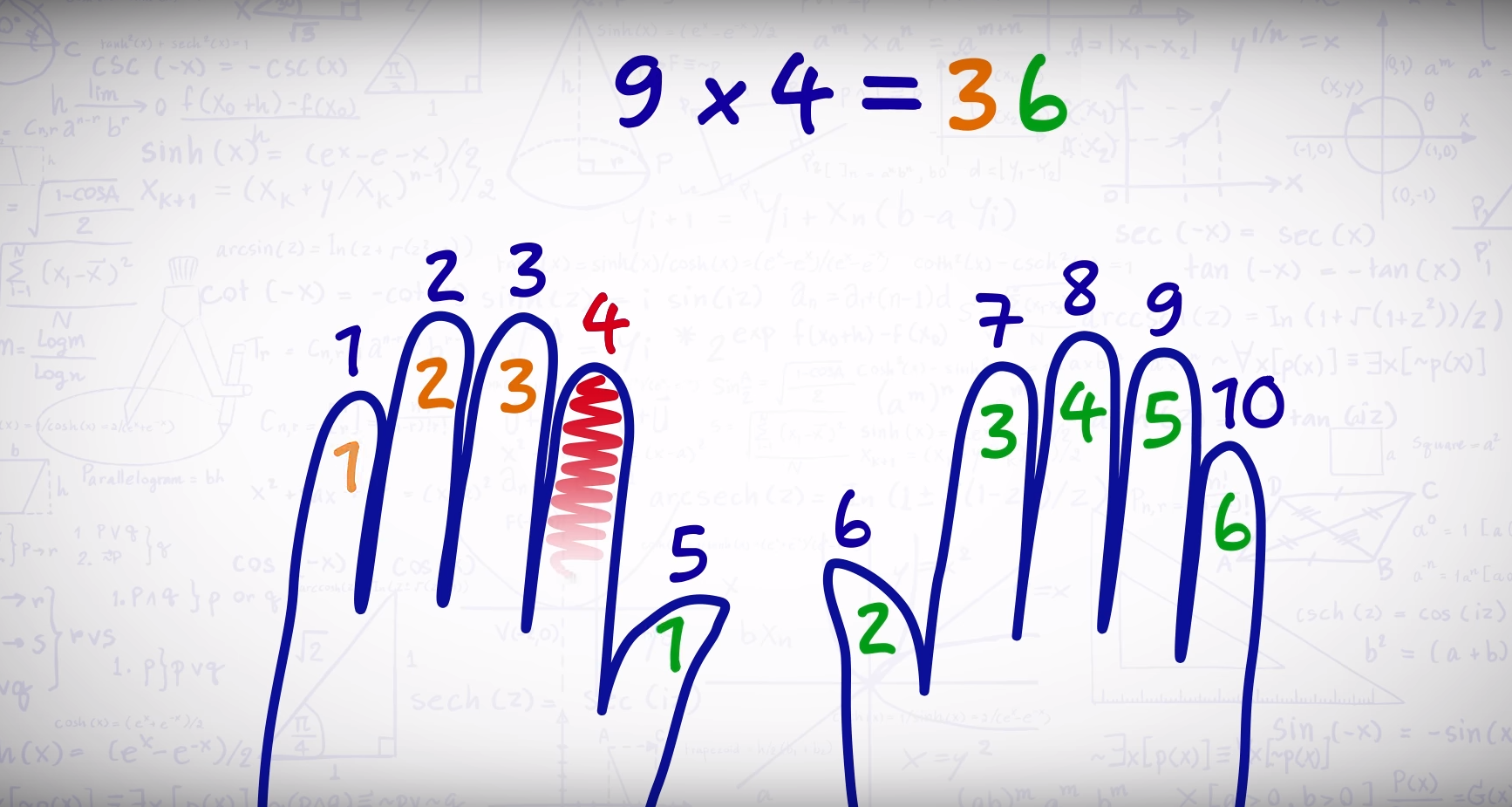
А для быстрых вычислений можно использовать собственные руки.
Для примера, умножим 4 на 9:
А теперь посложнее:
В буквальном смысле посчитали на пальцах.
Умножение на 11
Еще одно удобное число – 11. При умножении на него первая и последняя цифры результата заранее известны, а остальные получаются путем попарного сложения разрядов исходного числа.
Для примера умножим 11 на 32:
Слишком просто? Давайте возьмем пример посложнее и умножим 11 на 76:
Сумма цифр (7+6) здесь состоит из двух разрядов (13), а не из одного, как в предыдущем примере. Поэтому значение первого разряда (1) пришлось прибавить к первой цифре результата (7).
А теперь настоящий вызов: умножим 11 на 25816! Если вы сможете сделать это в уме, вы великолепны! Если нет, то воспользуйтесь этим методом.
Начинаем как раньше, с определения первой и последней цифр. А затем заполняем пропуски, складывая цифры попарно, начиная с конца:
Умножение больших чисел
Отличный метод для умножения чисел, близких к 100. С малыми значениями работать гораздо проще, чем с большими, поэтому мы заменим сами множители на их разность с сотней.
Вычитая из 100 числа 96 и 97 получим 4 и 3 – теперь это наши основные операнды.
Число Пи
Запомнить первые 7 цифр числа Пи поможет английский мнемоник
How I wish I could calculate Pi
Количество букв в каждом слове равно соответствующей цифре.
Математические пирамиды
Два замечательных примера арифметической симметрии, которые вы можете использовать для быстрых вычислений или математических трюков.
От Цельсия до Фаренгейта и обратно
Приходилось когда-нибудь переводить температуру по Цельсию в градусы Фаренгейта? Формула несложная, но запоминается плохо:
градусы Цельсия * 1.8 + 32 = градусы Фаренгейта
Для приблизительных подсчетов можно использовать более удобные значения: умножать на 2 и прибавлять 30.
Обратное преобразование состоит в вычитании 32 и делении на 1.8. Здесь также можно использовать упрощенную формулу:
Ментальная арифметика на пальцах
Содержание:
Ментальная арифметика. Что это такое
Где и когда можно заниматься
Методика ментальной арифметики пошаговая, состоящая из 10 уровней, из которых 5 уровней образуют базовую программу детского развития. Каждый уровень длится 4-6 месяцев, а все обучение базовой программы занимает 2-2,5 года.
Заниматься можно не только в специальных группах с педагогом, но и в домашних условиях с родителями. В группах мини-уроки обычно проходят 1-2 раза еженедельно по 30-45 мин. Дома можно упражняться через день по 15-20 мин.
На начальном уровне достигаются следующие цели:
Навык визуализации является значимым и переходным на следующий уровень. Если ребенок хорошо разовьет навык визуализации, то в дальнейшем быстро и самостоятельно сможет считать без счет в уме (ментально).
Счеты для ментальной арифметики. Какие и зачем
Потребность человека в количественном измерении, подсчете и математических расчетах появилась задолго до появления чисел. Первым расчетным инструментом, который природа предоставила в распоряжение человека, была его собственная рука/пальцы. Потом считать стали на ракушках, веточках, камешках и так далее.
Эти счеты состоят из нескольких частей:
Японский соборан или абакус напоминает наши, отечественные счеты, которые перевернули на бок.
Как быстро считать на абакусе. Общие правила
В счетах соробан имеет значение каждый элемент! Так:
Существует история, что в конце 1946 года японский почтовый чиновник, весьма искусный в использовании абакуса, вступил в соревнование с иностранным солдатом, который для счета использовал самый современный калькулятор. В четырех из пяти состязаний японский чиновник со счетами оказался быстрее, уступив лишь в сложных задачах.
Сложение и вычитание на абакусе
Прежде всего, нужно научиться откладывать числа на счетах. Например:
После того как дошкольник освоил цифры на абакусе, практику откладывания чисел, можно переходить к примерам простого сложения. Пошагово это происходит так:
С верхней 2ой спицы опускаем 2 бусины, с 1ой нижней поднимаем 3.
На 2ой и 1ой спицах возвращаем по 1-ной бусине.
Уроки ментальной арифметики по набору чисел, сложению/вычитанию можно предварительно смотреть в видео и сразу повторять с ребенком. Это особенно полезно, если занимаетесь сами, дома.
Умножение и деление на абакусе
Работаем с десятками: с нижней 3ей спицы поднимаем вверх 2-е бусины, 10 * 20 = 200.
Поднимаем на 2ой нижней спице вверх 4-е бусины, умножаем единицы первого числа на десятки, 2 * 20 = 40.
Опускаем на 2ой спице одну верхнюю бусину и все нижние, умножаем десятки первого числа на единицы второго, 10 * 1 = 10.
Поднимаем на 1ой нижней спице вверх 2-е бусины, умножаем единицы первого и второго числа, 2 * 1 = 2.
В результате: 12 * 21 = 252.
По мере тренировки и решения примеров приходит понимание действий, подсчет доводится до автоматизма.
После того, как хорошо усвоено умножение, можно приступать к примерам деления.
Выставляем в правой половине счет 62, левая пустая, для ответа.
Делим 6 на 2, получаем 3 и откладываем его на крайней левой спице.
В первой половине на 2ой спице отнимается 6-ть бусин остается 2.
На второй слева спице откладывается 1, которая получилась, когда 2 : 2.
Решение примера получается: 62 : 2 = 31.
Как перейти от абакуса к счету на пальцах
Для того, чтобы в последующих уроках начать представлять бусинки, желательно проделывать различные задания, развивающие образное мышление. Например, нахождение различий на картинках, пересказ содержимого в картинке и ответ на вопросы по рисунку, определение фигур на ощупь.
Как правило, обучение ментальной арифметике завершается тем, что ребенок без специальных счет, в уме, быстро решает любые примеры, хорошо запоминает действия, имеет развитое логическое и математическое мышление.
Плюсы и минусы ментальной арифметики
С помощью магнитно-резонансного теста (МРТ) исследователи доказали, что большинство людей (90%) в мире используют в основном левую сторону мозга для своей повседневной деятельности, включая регулярные школьные занятия. При этом правое полушарие мозга развивается недостаточно, поэтому воображение, фантазия, креативность, гибкость мышления развиты недостаточно.
Таким образом, чтобы повысить общий интеллект головного мозга необходимо межполушарное взаимодействие. Чтобы достичь полного развития мозга, мы и используем ментальную арифметику как средство и счеты как инструмент.
Уроки ментальной арифметики разрешены всем, независимо от пола, физической формы, они не имеют медицинских ограничений. Заниматься можно в группе и одному, дома, с родителями. Малыши с 4-х лет уже могут осваивать интересные счеты абакус и заниматься с игровым раздаточным материалом.
Есть ли минусы у ментальной математики? Многие педагоги подчеркивают важность правильного расписания занятий. Не перегрузить, чтобы не спровоцировать утомление и ухудшение результатов запоминания!
Еще один нюанс состоит в том, чтобы заниматься по плану, не перескакивая с темы на тему. В этом случае можно гарантировать стойкий результат и гармоничное развитие ребенка.
В школу с удовольствием
Подготовьте своего дошкольника к занятиям, используя методику ментальной арифметики. Он научится быстро считать, решать примеры и будет уверенно чувствовать себя на уроках. Учителя наверняка отметят гибкость его мышления, тягу к знаниям, которые вы развили с помощью менара!