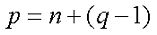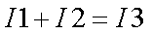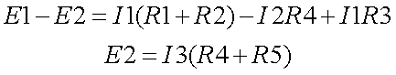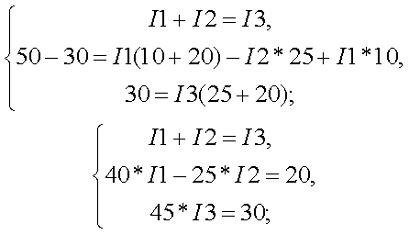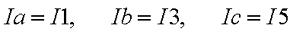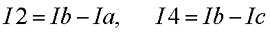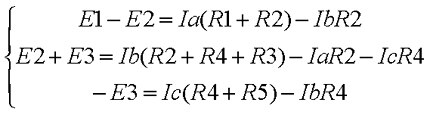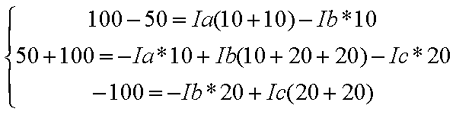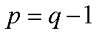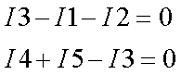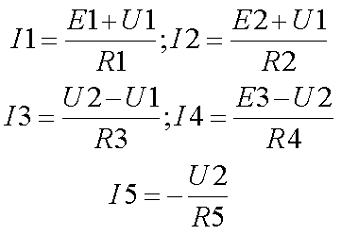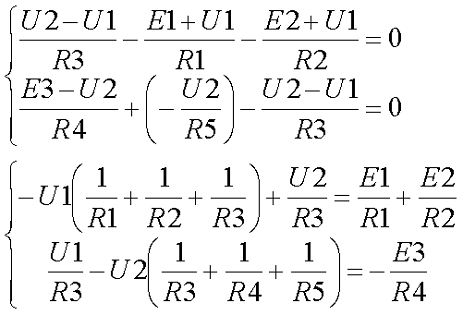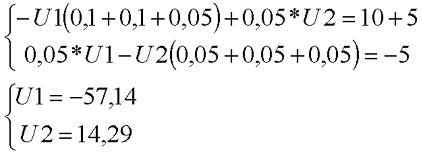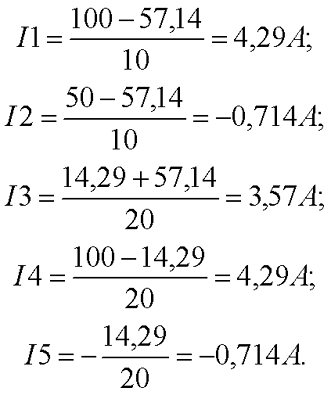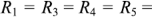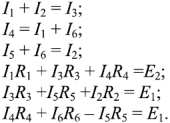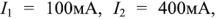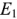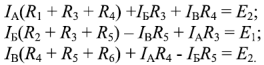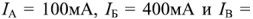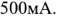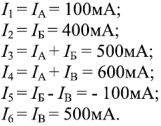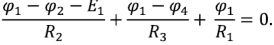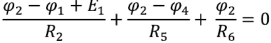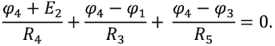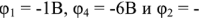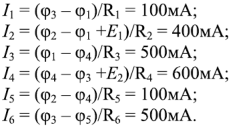какой метод расчета требует наименьшее число уравнений при расчете сложной цепи
ElectronicsBlog
Обучающие статьи по электронике
Электротехника Часть 5 Методы расчёта электрических цепей
Всем доброго времени суток. В прошлой статье я рассматривал типы соединений приемников энергии в электрических цепях, а так же законы Кирхгофа, которые определяют основные соотношения токов и напряжений в этих цепях. Но кроме знания основных законов электротехники необходимо уметь рассчитывать неизвестные параметры электрических цепей по заданным известным параметрам. Так, например, по известным напряжениям, ЭДС и сопротивлениям необходимо знать какую мощность будет потреблять тот или иной приемник энергии, а так же вся цепь в целом. Этим мы и займёмся в данной статье.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Расчёт электрических цепей с помощью законов Кирхгофа
Существует несколько методов расчёта электрических цепей, которые различаются между собой параметрами, которые необходимо найти, а так же количеством необходимых расчётов.
Вначале я расскажу, как произвести расчёт цепи в общем виде, но в результате размеры вычислений будут неоправданно большими. Данный метод расчёта основан на законах Ома и Кирхгофа и используется при расчётах небольших цепей с малым количеством контуров. Для этого составляют систему уравнений из (q — 1) уравнений для узлов цепи и n уравнений для независимых контуров. Независимые контуры характеризуются тем, что при составлении уравнений для каждого нового контура входит хотя бы одна новая ветвь, не вошедшая в предыдущий контур. Таким образом, количество уравнений в системе уравнений по данному методу расчёта цепи будет определяться следующим выражением
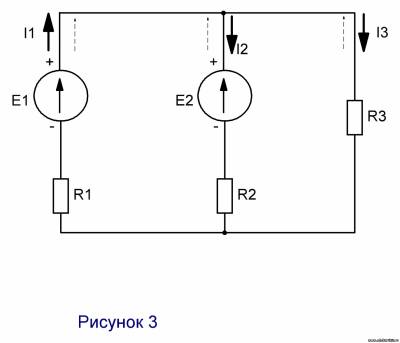
В качестве примера рассчитаем электрическую цепь, приведённую на рисунке ниже
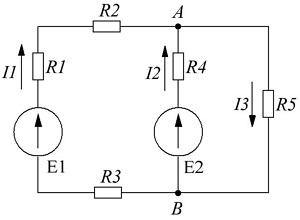
Пример электрической цепи для расчёта по законам Ома и Кирхгофа.
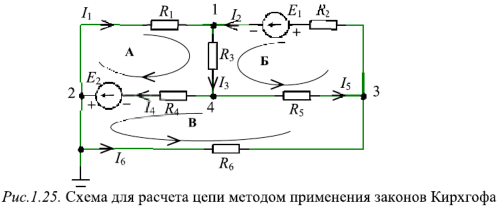
В качестве примера возьмём следующие параметры схемы: E1 = 50 B, E2 = 30 B, R1 = R3 = 10 Ом, R2 = R5 = 20 Ом, R4 = 25 Ом.
Таким образом, получившаяся система уравнений будет иметь следующий вид
Решив данную систему, получим следующие результаты: I1 ≈ 0,564 А, I2 ≈ 0,103 А, I2 ≈ 0,667 А.
В результате решения системы уравнений по данному методу может оказаться, что токи получились отрицательными. Это значит, что действительное направление токов противоположно по направлению выбранному.
Метод контурных токов
Рассмотренный выше метод расчета электрических цепей при анализе больших и разветвленных цепей приводит к неоправданно трудоемким расчетам, поэтому редко применяется. Более широко используется метод контурных токов, позволяющий значительно сократить количество уравнений. При этом вместо токов в ветвях электрической цепи определяются так называемые контурные токи при помощи второго закона Кирхгофа. Таким образом, количество требуемых уравнений будет равняться числу независимых контуров. В качестве примера рассчитаем цепь изображённую на рисунке ниже
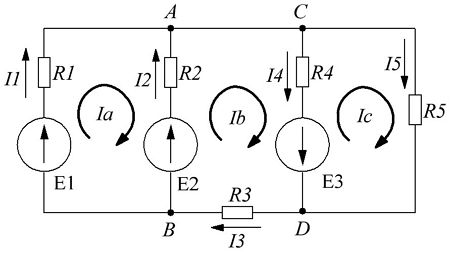
Расчет цепи методом контурных токов.
Если бы мы вели расчёт цепи по методу законов Ома и Кирхгофа, то необходимо было бы решить систему из пяти уравнений. Для расчёта по методу контурных токов необходимо всего три уравнения.
В начале расчёта выделяют независимые контуры, в нашем случае это: E1R1R2E2, E2R2R4E3R3 и E3R4R5. Затем контурам присваивают произвольно направленный контурный ток, который имеет одинаковое направление для всех участков выбранного контура, в нашем случае для первого контура контурный ток будет Ia, для второго – Ib, для третьего – Ic. Как видно из рисунка некоторые контурные токи соответствуют токам в ветвях
Остальные же токи можно найти как разность двух контурных токов
В результате выбора контурных токов можно составить систему уравнений по второму закону Кирхгофа
Рассчитаем схему, изображённую на рисунке выше со следующими параметрами E1 = E3 = 100 B, E2 = 50 B, R1 = R2 = 10 Ом, R3 = R4 = R5 = 20 Ом. Запишем систему уравнений
Метод узловых напряжений
Кроме метода контурных токов, для уменьшения трудоемкости расчётов, применяют метод узловых напряжений, при этом возможно еще меньшее число уравнений, так как при этом методе их число достигает
где q – количество узлов в электрической цепи.
Принцип расчёта электрической цепи заключается в следующем:
В качестве примера возьмём предыдущую цепь и составим систему уравнений
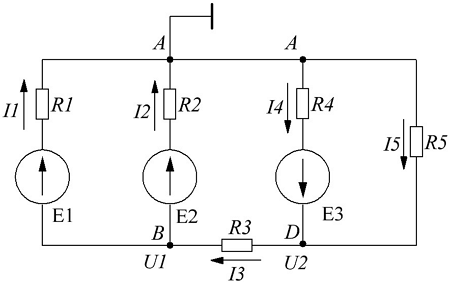
Схема для решения уравнений методом узловых потенциалов.
В качестве базисного возьмём узел А и заземлим его, для остальных узлов B и D составим уравнения по первому закону Кирхгофа
Примем потенциалы узлов В = U1 и D = U2, тогда токи в ветвях выразятся через обобщённый закон Ома
В результате получившаяся система будет иметь следующий вид
Рассчитаем схему, изображённую на рисунке выше со следующими параметрами E1 = E3 = 100 B, E2 = 50 B, R1 = R2 = 10 Ом, R3 = R4 = R5 = 20 Ом. Запишем систему уравнений
Результат решения для токов I2 и I5 получился отрицательным, так как действительное направление токов противоположно направлению, изображённому на рисунке. Данные результаты совпадают с результатами, полученными для этой же схемы при расчёте по методу контурных токов.
Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.
Какой метод расчета требует наименьшее число уравнений при расчете сложной цепи
Сложной электрической цепью называют цепь с несколькими замкнутыми контурами, с любым размещением в ней источников питания и потребителей, которую нельзя свести к сочетанию последовательных и параллельных соединений.
Основными законами для расчета цепей наряду с законом Ома являются два закона Кирхгофа, пользуясь которыми, можно найти распределение токов и напряжений на всех участках любой сложной цепи.
В § 2-15 мы ознакомились с одним методом расчета сложных цепей, методом наложения.
Сущность этого метода заключается в том, что ток в какой-либо ветви является алгебраической суммой токов, создаваемых в ней всеми поочередно действующими э. д. с. цепи.
Рассмотрим расчет сложной цепи методом узловых и контурных уравнений или уравнений по законам Кирхгофа.
Для нахождения токов во всех ветвях цепй необходимо знать сопротивления ветвей, а также величины и направления всех э. д. с.
Перед составлением уравнений по законам Кирхгофа следует произвольно задаться направлениями токов в ветвях, показав их на схеме стрелками. Если выбранное направление тока в какой-либо ветви противоположно действительному, то после решения уравнений этот ток получается со знаком минус.
Число необходимых уравнений равно числу неизвестных токов; число уравнений, составляемых по первому закону Кирхгофа, должно быть на единицу меньше числа узлов цепи, остальные уравнения составляются по второму закону Кирхгофа. При составлении уравнений по второму закону Кирхгофа следует выбирать наиболее простые контуры, причем каждый из них должен содержать хотя бы одну ветвь, не входившую в ранее составленные уравнения.
Расчет сложной цепи с применением двух уравнений Кирхгофа рассмотрим на примере.
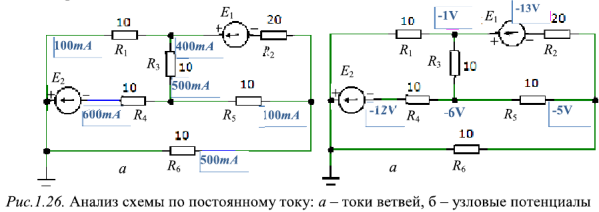
Пример 2-12. Вычислить токи во всех ветвях цепи рис. 2-11, если э. д. с. источников 
, а сопротивления ветвей 
.
Внутренними сопротивлениями источников пренебречь.
Рис. 2-11. Сложная электрическая цепь с двумя источниками питания.
Выбранные произвольно направления токов в ветвях показаны на рис. 2-11.
Так как число неизвестных токов три, то необходимо составить три уравнения.
При двух узлах цепи необходимо одио узловое уравнение. Напишем его для точки В:
4 Второе уравнение напишем, обходя по направлению движения часовой стрелки контур АБВЖЗА,
Третье уравнение напишем, обходя по направлению движения часовой стрелки контур АГВЖЗА,
Заменив в уравнениях (2-49) и (2-50) буквенные обозначения числовыми значениями, получим:
Заменив в последнем уравнении ток 
его выражением 
уравнения (2-48), получим;
(2-52а)
Умножив уравнение (2-52а) на 0,3 и сложив с уравнением (2-51), получим:
откуда определяется ток в третьей ветви:
Напряжение на концах третьей ветви
Токи в первой и второй ветвях:
Полученное отрицательное значение тока 
указывает на то, что в действительности этот ток направлен противоположно указанному на схеме (рис. 2-11). Таким образом, источник 
работает в рейшме генератора, а источник 
— в режиме двигателя.
Какой метод расчета требует наименьшее число уравнений при расчете сложной цепи
Методы расчета сложных электрических цепей постоянного тока
1. Метод узловых и контурных уравнений
В основе расчета лежат первый и второй законы Кирхгофа.
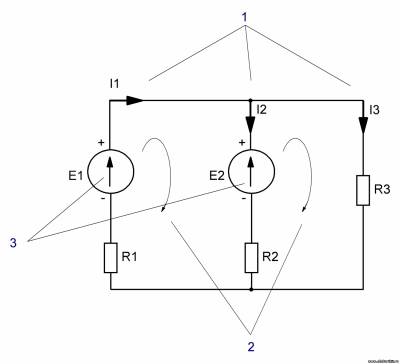
Итак, на схеме рисуем направления токов (1), согласно этим направлениям рисуем направления обхода контуров (2), согласно полярности источников питания ставим направления ЭДС (3).
Согласно первому закону Кирхгофа:
Теперь составляем уравнения по второму закону Кирхгофа:
Получили систему из трех уравнений. Решаем.
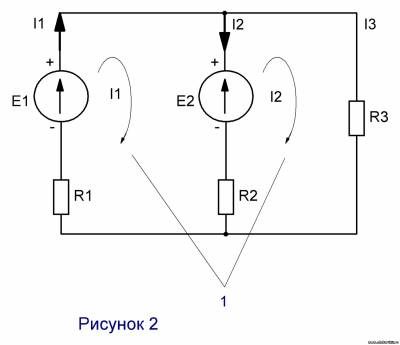
2. Метод контурных токов
Этот метод основан на втором законе Кирхгофа
3. Определяем истинные токи.
3. Метод двух узлов
Этот метод применим для схем, имеющих два узла
Так как, значения I2 и I3 получились отрицательными, то эти токи будут противоположными по направлению (на рисунке показаны жирные сплошные стрелки).
4. Метод наложения или метод суперпозиции
Метод основан на том, что любой ток в цепи создается совместным действием всех источников питания. Поэтому можно рассчитать частичные токи от действия каждого источника питания отдельно, а затем, найти истинные токи как арифметическую составляющую частичных.
Методы расчета сложных электрических цепей
Методы расчета сложных электрических цепей
Сложной электрической цепью называют разветвленную цепь с несколькими источниками электрической энергии. Применение методов эквивалентных преобразований в таких цепях, как правило, не эффективно, так как не позволяют упростить ее до одноконтурной цепи или цепи с двумя узлами. Для расчета таких цепей используют более общие методы.
Метод непосредственного применения законов Кирхгофа
Метод заключается в составлении системы уравнений с применением первого и второго законов Кирхгофа для заданной электрической цени, решение которой позволяет определить токи всех ветвей цепию.
Реализация этою метода, как и любого другого метода расчета сложной электрической цени, начинается с предварительного анализа ее схемы с целью определения числа узлов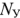 
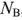
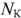
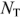
, числа ветвей 
, числа независимых контуров 
, числа ветвей 
с источниками токов, выяснения возможности упрощения схемы.
Прежде всего определяют число неизвестных токов, которое равно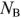 
— 
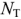
. Для каждой ветви задают положительное направление тока.
Далее по первому закону Кирхгофа составляют 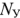— 1 независимых уравнений.
Затем по второму закону составляют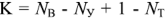 
уравнений. При этом выбирают независимые контуры, не содержащие источников тока.
Общее число составленных по первому и второму законам Кирхгофа должно быть равно числу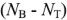 
неизвестных токов.
Рассмотрим применение законов Кирхгофа для определения токов в ветвях цепи, схема которой приведена на рис. 1.25. Пусть ЭДС идеальных источников напряжения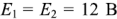 
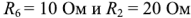
, сопротивления 
. Требуется определить все токи схемы с помощью метода непосредственного применения законов Кирхгофа.
Схема содержит 6 ветвей с неизвестными токами и четыре узла. Па схеме узлы обозначены арабскими цифрами, показаны принятые направления токов и направления обхода контуров А, Б и В.
Составим систему из 6 уравнений. Уравнения по первому закону Кирхгофа запишем для узлов 1, 2, 3, уравнения по второму закону Кирхгофа запишем для контуров А, Б, В:
Решив эту систему уравнений, получим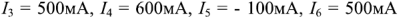 
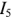
. Отрицательное значение тока 
, указывает на то, что выбранное при составлении уравнений направление этого тока не соответствует действительности. Правильное направление — от узла 3 к узлу 4.
Для проверки вычислений с помощью программы схемотехнического моделирования Micro Сар выполнен анализ по постоянному току схемы, изображенной на рис. 1.25. Изображенные на рис. 1.26,а значения токов ветвей (в мА) подтверждают правильность выполненных расчетов. Изображенные на рис. 1.26,б узловые потенциалы схемы (в В) позволяют определить направление токов ветвей.
Метод контурных токов
Метод контурных токов наиболее часто применяется на практике для расчета сложных цепей, так как он позволяет находить все неизвестные величины при числе уравнений, меньшем числа неизвестных величин.
По этому методу в каждом независимом контуре схемы вместо действительных токов в ветвях вводят условный контурный ток. Действительный ток в любой ветви, принадлежащей только одному контуру, численно равен контурному току. Действительный ток в любой ветви, принадлежащей нескольким контурам равен алгебраической сумме контурных токов, проходящих через эту ветвь.
Падение напряжения при прохождении тока смежного контура в элементе принимают положительным, если направление тока в смежном контуре совпадает с направлением обхода, Если направление тока смежного контура не совпадает с направлением обхода, падение напряжения считают отрицательным. Значение ЭДС берется со знаком плюс, если направление обхода контура совпадает с положительным направлением ЭДС, и со знаком минус — если не совпадает.
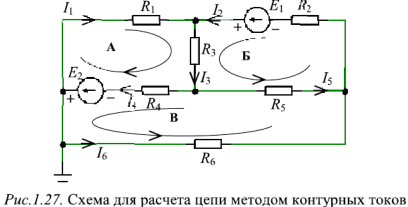
Метод контурных токов рассмотрим на примере схемы электрической цепи, изображенной на рис. 1.27. Схема имеет три независимых контура: А, Б, В. Через сопротивления каждого контура проходит свой контурный ток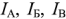 
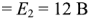
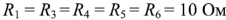
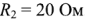
. Направления обхода каждого контура совпадает с направлением контурного тока этого контура. ЭДС идеальных источников напряжения 
, сопротивления 
и 
.
Уравнения, составленные по второму закону Кирхгофа, для контуров А, Б и В:
Подставив в эту систему уравнений численные значения ЭДС источников и сопротивлений и решив ее, получим 
Действительные токи ветвей схемы:
Полученные значения полностью совпадают с результатами ранее проделанного расчета этой же цени по методу непосредственного применения Законов Кирхгофа.
Метод узловых потенциалов
Потенциал любой точки электрической цепи определяется напряжением между данной точкой и точкой цепи с потенциалом равным нулю.
Метод узловых потенциалов заключается в том, что вначале полагают равным нулю потенциал некоторого базисного узла и для оставшихся (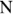 
-1) узлов составляют уравнения по первому закону Кирхгофа: алгебраическая сумма токов всех ветвей, подключенных к рассматриваемому узлу равна нулю. При этом токи ветвей, соединяющих узлы, определяются с помощью обобщенного закона Ома. Решив полученную систему уравнений, определяют потенциалы узлов.
Далее, применив обобщенный закон Ома для ветвей, определяют искомые токи.
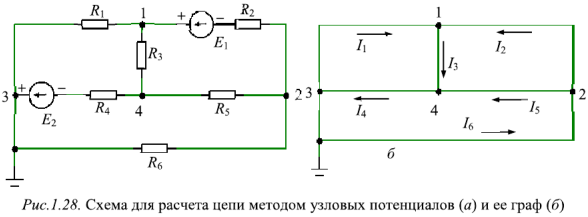
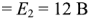
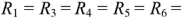
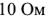
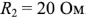
Метод узловых потенциалов рассмотрим на примере схемы электрической цепи, изображенной на рис. 1.28 (я). В этой схеме ЭДС идеальных источников напряжения , сопротивления 
и 
.
Схема имеет четыре узла. Примем потенциал узла 3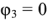 
. Составляем уравнения по методу узловых потенциалов. Сумма токов узла 1 приравнивается нулю. Ток каждой ветви, подключенной к узлу 1, записывается в соответствии с обобщенным законом Ома
Аналогично для узла 2
Подставив в полученную систему уравнений численные значения ЭДС источников и сопротивлений и решив ее, получим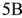 
. Полученные результаты совпадают с данными (рис. 1.26,6^, полученными при выполнении с помощью программы Micro-Сар анализа по постоянному току схемы, изображенной на рис. 1.28,а.
Применив обобщенный закон Ома для каждой ветви схемы, получим искомые токи:
Полученные значения токов совпадают с результатами расчета этой цепи методом непосредственного применения законов Кирхофа и методом контурных токов.
Направления найденных токов указаны на графе цепи на рис. 1.28,6. Графом цепи называют такое изображение схемы электрической цепи, в котором все ветви заменены линиями, источники напряжения закорочены, а источники тока разомкнуты. Все ветви и все узлы сохраняются.
Метод узловых потенциалов имеет преимущество перед методом контурных токов в том случае, когда число уравнений, записанных по первому закону Кирхгофа, меньше числа уравнений, записанных по второму закону Кирхгофа.
Метод двух узлов является частным вариантом метод узловых потенциалов. Он применяется в тех случаях, когда анализируемая схема содержит только два узла (для определенности узлы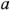 
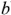
и 
) и большое число параллельных ветвей, содержащих и не содержащих источники ЭДС. Согласно методу двух узлов межузловое напряжение
где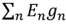 
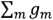
— алгебраическая сумма произведений ЭДС ветвей (ЭДС считаются положительными, если они направлены к узлу , и отрицательными, если от узла к узлу ) на проводимости этих ветвей; 
— сумма проводимости всех ветвей, соединяющих узлы и .
Эта теория взята со страницы помощи с заданиями по электротехнике:
Возможно эти страницы вам будут полезны:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института