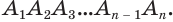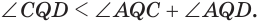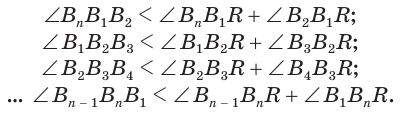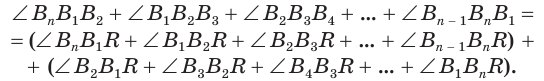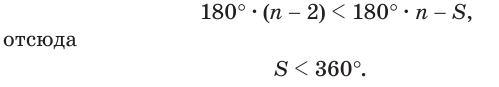какой многогранник существует в геометрии ответ миллионер

Геометрия. 10 класс

Конспект урока

Геометрия, 10 класс

Урок № 16. Правильные многогранники

Перечень вопросов, рассматриваемых в теме:

Правильный многогранник – выпуклый многогранник, все грани которого равные правильные многоугольники и в каждой его вершине сходится одно и то же число ребер.

Правильный тетраэдр – многогранник, составленный из четырех равносторонних треугольников.

Правильный октаэдр – многогранник, составленный из восьми равносторонних треугольников.

Правильный икосаэдр – многогранник, составленный из двадцати равносторонних треугольников.

Куб (гексаэдр) – многогранник, составленный из шести квадратов.

Правильный додекаэдр – многогранник, составленный из двенадцати правильных пятиугольников.

Точки А и А1 называются симметричными относительно точки О, если О – середина отрезка АА1.

Точки А и А1 называются симметричными относительно прямой а, если прямая а проходит через середину отрезка АА1 и перпендикулярна этому отрезку.

Точки Аи А1 называются симметричными относительно плоскости α, если плоскость α проходит через середину отрезка АА1 и перпендикулярна этому отрезку.

Точка (прямая, плоскость) называется центром (осью, плоскостью) симметрии фигуры, если каждая точка фигуры симметрична относительно нее некоторой точке той же фигуры.

Потоскуев Е.В., Звавич Л. И. Геометрия. 11кл.: учеб. Для классов с углубл. И профильным изучением математики общеобразоват. Учреждений – М.: Дрофа, 2009. – 368 с.: ил. (128 с. – 131 с.)

Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10–11 классы : учеб. Для общеобразоват. организаций : базовый и углубл. уровни – М.: Просвещение, 2014. – 255 с. (68 с. – 73 с.)

Открытые электронные ресурсы:

Многогранники.ru – сайт о создании моделей многогранников из бумаги https://www.mnogogranniki.ru/

Теоретический материал для самостоятельного изучения

Также нам уже знаком правильный тетраэдр.

Заметьте, что правильный тетраэдр и правильная треугольная пирамида – это различные многогранники!

Напомним, что пирамида называется правильной, если в основании лежит правильный многоугольник, а основание высоты совпадает с центром многоугольника. Таким образом, в правильной треугольной пирамиде боковые ребра равны друг другу, но могут быть не равны ребрам основания пирамиды, а в правильном тетраэдре все ребра равны.

Правильных многогранников существует всего 5. Перечислим их.

Правильный тетраэдр – многогранник, составленный из четырех равносторонних треугольников. Каждая его вершина является вершиной трех треугольников, значит сумма плоских углов при каждой вершине равна 180.

Правильный октаэдр – многогранник, составленный из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной четырех треугольников, значит, сумма плоских углов при каждой вершине равна 240.

Куб (гексаэдр) – многогранник, составленный из шести квадратов. Каждая вершина куба является вершиной трех квадратов, значит, сумма плоских углов при

каждой вершине равна 270.

Правильный икосаэдр – многогранник, составленный из двадцати равносторонних треугольников. Каждая вершина икосаэдра является вершиной пяти треугольников, значит, сумма плоских углов при каждой равна 300.

Рисунок 4 – Правильный икосаэдр

Правильный додекаэдр – многогранник, составленный из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трех правильных пятиугольников, значит, сумма плоских углов при каждой равна 324.

Рисунок 5 – Правильный додекаэдр

Докажем, что правильных многогранников существует ровно 5, то есть что не существует правильного многогранника, гранями которого являются правильные n-угольники при n≥6.

По этой причине каждая вершина правильного многогранника может быть вершиной либо трех, либо четырех, либо пяти равносторонних треугольников, либо трех квадратов, либо трех правильных пятиугольников.

Симметрия в пространстве

Одно из интересных свойств правильных многогранников – это элементы симметрии.

Прежде чем мы их выделим давайте определим симметрию в пространстве.

Вам уже знакома симметрия из курса планиметрии. Там мы рассматривали фигуры симметричные относительно прямой и точки. В стереометрии же рассматривают симметрию относительно точки, прямой и плоскости.

Будем говорить, что точки А и А1 симметричны относительно точки О (рис. 6), если О – середина отрезка АА1. В таком случае О будет являться центром симметрии и будет симметрична сама себе.

Рисунок 6 – Центральная симметрия

Точки А и А1 называются симметричными относительно прямой а, если прямая а проходит через середину отрезка АА1 и перпендикулярна к этом отрезку (рис. 7). Прямая а называется осью симметрии, а каждая ее точка считается симметричной самой себе.

Рисунок 7 – Осевая симметрия

Точки АА1 называются симметричными относительно плоскости α, если плоскость α проходит через середину отрезка АА1 и перпендикулярна к этому отрезку (рис. 8). Плоскость α называется плоскостью симметрии, а каждая ее точка считается симметричной самой себе.

Точка (прямая, плоскость) называется центром (осью, плоскостью) симметрии фигуры, если каждая точка фигуры симметрична относительно нее некоторой точке той же фигуры.

Если фигура имеет центр (ось, плоскость) симметрии, то говорят, что она обладает центральной (осевой, зеркальной) симметрией.

Рисунок 8 – Зеркальная симметрия

Рисунок 9 – Элементы симметрии куба

Примером фигуры, обладающей и центральной, и осевой и зеркальной симметрией является куб (рис. 9).

Фигура может иметь один или несколько центров (осей, плоскостей) симметрии. Так, например, у куба один центр симметрии и несколько осей и плоскостей симметрии.

В геометрии центр, ось и плоскость симметрии многогранника называют элементами симметрии многогранников.

С симметрией мы часто можем встретиться в природе, архитектуре, быту.

Например, многие кристаллы имеют центр ось или плоскость симметрии.

Многие здания симметричны относительно плоскости. Примером такого здания является здание Московского государственного университета.

Рисунок 10 – Здание Московского государственного университета

Примеры и разбор решения заданий тренировочного модуля

№1 Выберите неверные утверждения

1) правильный додекаэдр состоит из 8 правильных треугольников

2) тетраэдр имеет 4 грани

3) гексаэдр состоит из шести параллелограммов

4) правильный октаэдр состоит из правильных пятиугольников

Утверждение под номером 1 неверно, так как название «додекаэдр» с греческого означает «двенадцать граней». В действительности, додекаэдр состоит из двенадцати правильных пятиугольников.

Утверждение 2 верно. Тетраэдр с греческого означает 4 грани и состоит тетраэдр из 4-х треугольников.

Гексаэдр, он же куб состоит из квадратов, которые в свою очередь являются параллелограммами, поэтому утверждение 3 верно.

С греческого «октаэдр» означает 8 граней, состоять в таком случае из пятиугольников он не может. Октаэдр состоит из восьми треугольников. Утверждение 4 неверно.

№ 2 Установите соответствие между правильными многогранниками и их развертками.

1) 2) 3) 4)

5) 6)

7) 8)

9) 10)

Для выполнения этого задания необходимо понять, из каких многоугольников составлен многогранник.

Итак, куб состоит из квадратов. Единственная развертка, состоящая из квадратов это развертка под номером 6. Проверить себя можно и мысленно сложив из развертки кубик.

Многогранник под номером 2 – тетраэдр, состоит из четырех треугольников. Поэтому ему будет соответствовать развертка под номером 7. Мысленно сложите из развертки тетраэдр.

Октаэдр состоит из 8 треугольников, в этом несложно убедиться исходя из изображения. Развертка под номером 8 как раз состоит из 8 треугольников.

Многогранник под номером 4 состоит также из треугольников, а единственная развертка, состоящая из треугольников, осталась под номером 10. Попробуйте вырезать такую развертку из бумаги и собрать свой икосаэдр!

Многогранник под номером 5 состоит из пятиугольников. Оставшаяся развертка 9 тоже состоит из пятиугольников. Осталось проверить, что количество совпадает.

Источник

Какой многогранник существует в геометрии ответ миллионер

Кратко охарактеризуем геометрические свойства некоторых многогранников:

а) модель		б) эпюр
Рисунок 67. Пирамида

2. Призма — многогранник, две грани которого (основания призмы) представляют собой равные многоугольники с взаимно параллельными сторонами, а все другие грани параллелограммы. Призма называется прямой, если её ребра перпендикулярны плоскости основания. Если основанием призмы является прямоугольник, призму называют параллелепипедом (рис. 68).

а) модель		б) эпюр
Рисунок 68. Призма

3. Призматоид — многогранник, ограниченный двумя многоугольниками, расположенными в параллельных плоскостях (они являются его основаниями); его боковые грани представляют собой треугольники или трапеции, вершины которых являются и вершинами многоугольников оснований (рис.69).

а) модель		б) эпюр
Рисунок 69. Призматоид

4. Тела Платона. Многогранник, все грани которого представляют собой правильные и равные многоугольники, называют правильными . Углы при вершинах такого многогранника равны между собой.

Существует пять типов правильных многогранников. Эти многогранники и их свойства были описаны более двух тысяч лет назад древнегреческим философом Платоном, чем и объясняется их общее название.

Каждому правильному многограннику соответствует другой правильный многогранник с числом граней, равным числу вершин данного многогранника. Число ребер у обоих многогранников одинаково.

а) модель		б) эпюр
Рисунок 70. Тетраэдр

Гексаэдр — правильный шестигранник (рис. 71). Это куб состоящий из шести равных квадратов.

а) модель		б) эпюр
Рисунок 71. Гексаэдр

Октаэдр — правильный восьмигранник ( рис.72). Он состоит из восьми равносторонних и равных между собой треугольников, соединенных по четыре у каждой вершины.

а) модель		б) эпюр
Рисунок 72. Октаэдр

Додекаэдр — правильный двенадцатигранник, состоит из двенадцати правильных и равных пятиугольников, соединенных по три около каждой вершины (рис. 73).

а) модель		б) эпюр
Рисунок 73. Додекаэдр

Икосаэдр — состоит из 20 равносторонних и равных треугольников, соединенных по пять около каждой вершины (рис.74).

а) модель		б) эпюр
Рисунок 74. Икосаэдр

5. Звездчатые формы и соединения тел Платона. Кроме правильных выпуклых многогранников существуют и правильные выпукло-вогнутые многогранники. Их называют звездчатыми (самопересекающимися). Рассматривая пересечения продолжения граней Платоновых тел, мы будем получать звездчатые многогранники.

Источник

Правильные многогранники в геометрии с примерами

Пусть есть плоский многоугольник

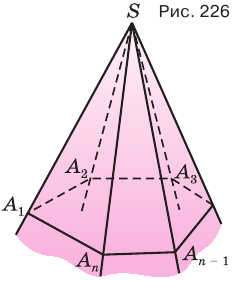
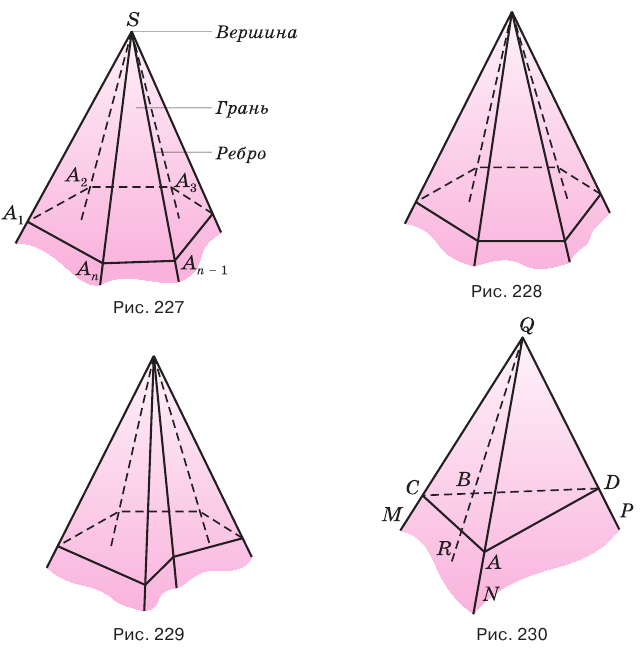
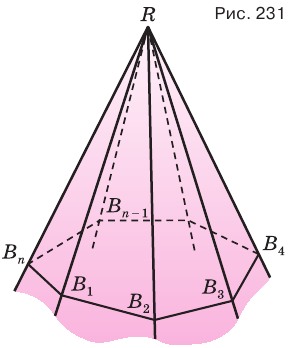
Многогранный угол называется выпуклым, если он расположен по одну сторону от плоскости любой его грани. Многогранный угол на рисунке 228 выпуклый, а на рисунке 229 — невыпуклый. По количеству граней многогранные углы разделяют на трехгранные, четырехгранные и т. д.

Теорема 12.

Сумма плоских углов выпуклого многогранного угла меньше 360°.

Доказательство:

Установим сначала, что каждый плоский угол трехгранного угла меньше суммы двух других его углов.

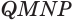
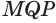
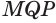
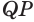
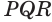
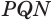
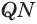
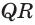
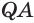
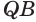
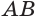
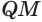
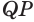
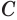
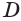
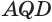
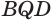
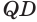
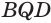
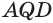
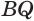
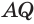
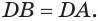
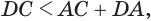
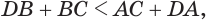
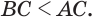
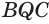
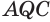
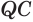
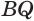
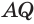
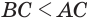
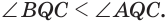
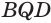
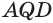
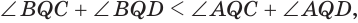
Пусть есть трехгранный угол (рис. 230). Пусть для определенности угол — больший из плоских углов трехгранного угла. В плоскости грани от луча отложим угол , равный углу , и на лучах и отложим равные отрезки и . Через прямую проведем такую плоскость, которая пересекает ребра и в некоторых точках и . Треугольники и равны, так как у них сторона общая, и по построению равны углы и , а также стороны и . Значит, Далее по свойству сторон треугольника получаем или или Теперь, поскольку у треугольников и сторона общая, стороны и равны, но , то Прибавив к левой и правой частям этого неравенства соответственно углы и , которые равны друг другу, получим, что или

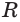
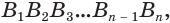
Пусть теперь есть выпуклый многогранный угол с вершиной (рис. 231). Если пересечь его какой-либо плоскостью, то в сечении получим многоугольник каждая вершина которого является вершиной трехгранного угла, образованного двумя гранями данного угла и секущей плоскостью. По доказанному для этих трехгранных углов получаем:

Сложим покомпонентно эти неравенства:

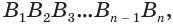
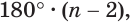
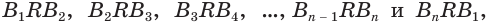
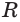
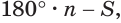
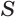
Теперь обратим внимание на то, что сумма в левой части последнего неравенства есть сумма углов многоугольника которая равна а в правой — сумма углов всех треугольников но без их углов при вершине , которая равна где выражает сумму плоских углов данного многогранного угла. Таким образом,

Многогранник, у которого все грани являются равными правильными многоугольниками и все двугранные углы равны друг другу, называется правильным многогранником.

Из этого определения следует, что у правильного многогранника равны друг другу все его:

Теорема 13.

Количество ребер, сходящихся в каждой вершине правильного многогранника, не больше пяти.

Доказательство:

Допустим, что это не так, т. е. в вершине многогранника сходится шесть или больше ребер. Тогда при этой вершине многогранник имел бы шесть или больше равных плоских углов. Учитывая, что сумма этих углов меньше 360°, получаем, что каждый из них меньше 60°. Но это невозможно, поскольку гранями правильного многогранника являются правильные многоугольники, а у них углы не меньше 60°.

Теорема 14.

Количество сторон правильного многоугольника, являющегося гранью правильного многогранника, не больше пяти.

Доказательство:

В каждой вершине правильного многогранника сходится не менее трех плоских углов, а поэтому каждый из них должен быть меньше 120°. Вместе с этим угол правильного шестиугольника равен 120°, а угол правильного многоугольника с большим количеством сторон больше 120°. Поэтому правильные многоугольники, количество сторон которых больше пяти, не могут быть гранями правильного многоугольника.

Теорема 15.

Есть пять типов правильных многогранников.

Доказательство:

В соответствии с теоремой 14 гранями многогранника могут быть правильные треугольники, четырехугольники или пятиугольники.

Если гранями правильного многогранника служат треугольники, то, с учетом теоремы 13, в вершинах многогранника могут сходиться три, четыре или пять ребер. Если гранями правильного многогранника служат четырехугольники или пятиугольники, то в вершинах многогранника может сходиться только три ребра. Значит, существует не более пяти видов правильных многогранников.

Чтобы убедиться, что такие виды многогранников существуют, достаточно указать способ построения каждого из них.

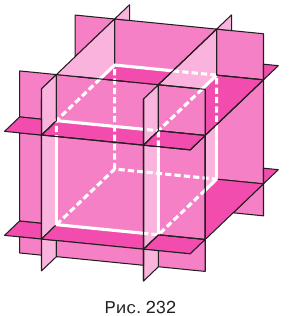
Прежде всего отметим, что правильным многогранником, гранями которого служат правильные четырехугольники, т. е. квадраты, является куб, который еще называют правильным гексаэдром. Куб можно построить так. В произвольно выбранной плоскости построить квадрат, через его стороны провести плоскости, перпендикулярные выбранной плоскости, и провести еще одну плоскость, параллельную выбранной плоскости и отстоящую от нее на сторону квадрата (рис. 232). Мы видим, что гексаэдр имеет 6 граней, 12 ребер и 8 вершин.

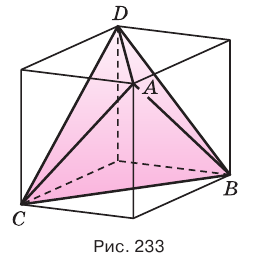
Построение многогранника, в каждой вершине которого сходится по три треугольные грани, может быть таким. Построить куб. Выбрать одну из его вершин и в каждой грани с этой вершиной выбрать вершину, противолежащую вершине . Пусть это вершины , , . Точки , , , являются вершинами искомого многогранника (рис. 233). Действительно, каждый из отрезков является диагональю одной из граней куба, а поэтому все эти отрезки равны друг другу. Получается, что в треугольной пирамиде все грани являются правильными треугольниками. Такая пирамида называется правильным тетраэдром. Тетраэдр имеет 4 грани, 6 ребер и 4 вершины.

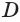
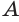
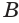
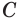
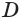
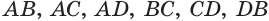
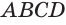
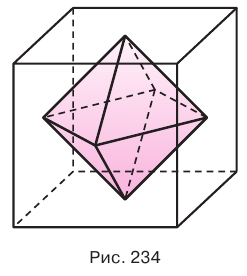
Построение многогранника, в каждой вершине которого сходится по четыре треугольные грани, может быть таким. Построить куб и найти центры шести его граней (рис. 234). Эти точки являются вершинами многогранника, все грани которого — правильные треугольники. Такой многогранник называется правильным октаэдром. Октаэдр имеет 8 граней, 12 ребер и 6 вершин.

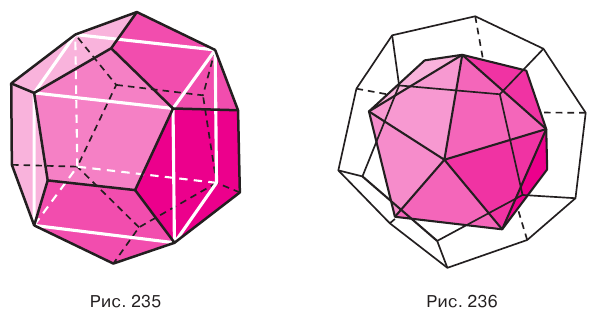
Построение многогранника, в каждой вершине которого сходится по три пятиугольные грани, можно выполнить, снова используя куб. Если через каждое из двенадцати ребер куба провести плоскость, которая не имеет с поверхностью куба других общих точек, кроме точек этого ребра, то полученные 12 плоскостей при пересечении дадут грани некоторого многогранника. Можно так подобрать наклон этих плоскостей к граням куба, что грани этого двенадцатигранника будут правильными пятиугольниками (рис. 235). Такой многогранник называется правильным додекаэдром. Додекаэдр имеет 12 граней, 30 ребер и 20 вершин.

Наконец, многогранник, в каждой вершине которого сходится по пять треугольных граней, можно построить, используя додекаэдр: центры граней додекаэдра являются вершинами искомого правильного многогранника (рис. 236). Такой многогранник называется правильным икосаэдром. Икосаэдр имеет 20 граней, 30 ребер и 12 вершин.

Таким образом, есть пять типов правильных многогранников.

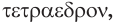
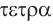
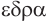
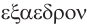
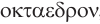
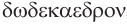
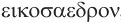
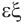
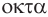
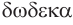
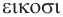
Названия правильных многогранников происходят из греческого языка. Термин тетраэдр, по-гречески означает четырехгранник: — четыре и — грань. Соответственно термины гексаэдр, октаэдр, додекаэдр, икосаэдр, по-гречески , , , , означают шестигранник, восьмигранник, двенадцатигранник, двадцатигранник: , — шесть, — восемь, — двенадцать, — двадцать.

Мы знаем, что правильные гексаэдр и тетраэдр имеют описанный и вписанный шары. Также описанный и вписанный шары имеют октаэдр, додекаэдр и икосаэдр. Центры этих шаров совпадают, и эта точка является центром симметрии соответствующего правильного многогранника, кроме тетраэдра, который не имеет центра симметрии.

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник