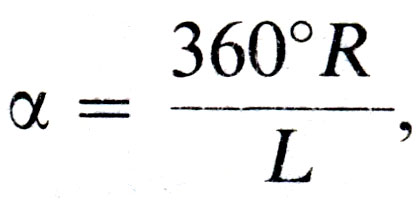какой знак должен сопровождать чертежи разверток
§ 16. Чертежи разверток поверхностей геометрических тел
16.1. Чертежи разверток поверхностей призм и цилиндров.
Для изготовления ограждений станков, вентиляционных труб и некоторых других изделий вырезают из листового материала их развертки.
Развертка поверхностей любой прямой призмы представляет собой плоскую фигуру, составленную из боковых граней — прямоугольников и двух оснований — многоугольников.
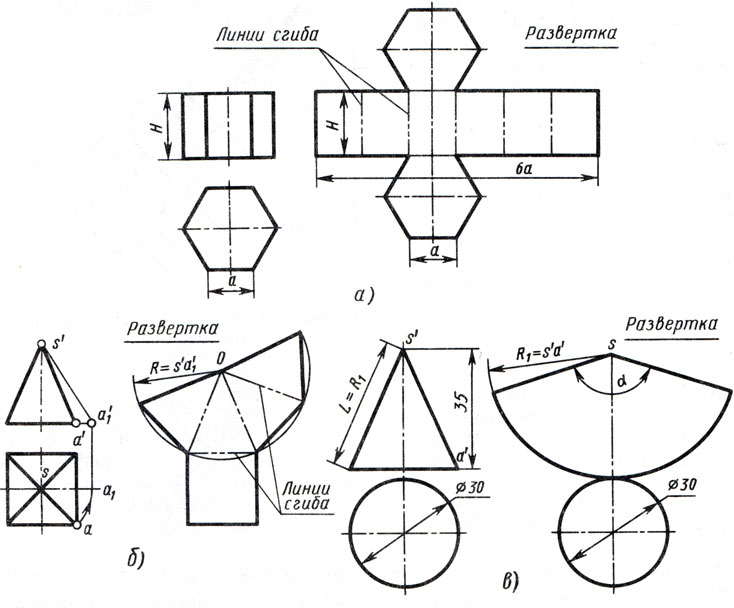
Например, у развертки поверхностей шестиугольной призмы (рис. 139, б) все грани — равные между собой прямоугольники шириной а и высотой h, а основания — правильные шестиугольники со стороной, равной а.
Рис. 139. Построение чертежа развертки поверхностей призмы: а — два вида; б — развертка поверхностей
Таким образом, можно построить чертеж развертки поверхностей любой призмы.
Развертка поверхностей цилиндра состоит из прямоугольника и двух кругов (рис. 140, б). Одна сторона прямоугольника равна высоте цилиндра, другая — длине окружности основания. На чертеже развертки к прямоугольнику пристраивают два круга, диаметр которых равен диаметру оснований цилиндра.
16.2. Чертежи разверток поверхностей конуса и пирамиды.
Рис. 141. Построение чертежа развертки поверхностей конуса: а — два вида; б — развертка поверхностей
Длину окружности при построении сектора можно определить по формуле C = 3.14xD.
Угол а подсчитывают по формуле а = 360°хD/2L, где D — диаметр окружности основания, L —длина образующей конуса, ее можно подсчитать по теореме Пифагора.
Рис. 142. Построение чертежа развертки поверхностей пирамиды: а — два вида; б — развертка поверхностей
Чертеж развертки поверхностей пирамиды строят так (рис. 142, б):
Из произвольной точки О описывают дугу радиуса L, равного длине бокового ребра пирамиды. На этой дуге откладывают четыре отрезка, равные стороне основания. Крайние точки соединяют прямыми с точкой О. Затем пристраивают квадрат, равный основанию пирамиды.
Какой знак должен сопровождать чертежи разверток
§ 24. Построение разверток поверхностей тел
Для изготовления кожухов машин, ограждений станков, вентиляционных устройств, трубопроводов необходимо из листового материала вырезать их развертки.
Разверткой поверхности многогранника называют плоскую фигуру, полученную при совмещении с плоскостью чертежа всех граней многогранника в последовательности их расположения на многограннике.
Чтобы построить развертку поверхности многогранника, нужно определить натуральную величину граней и вычертить на плоскости последовательно все грани. Истинные размеры ребер граней, если они спроецированы не в натуральную величину, находят способами вращения или перемены плоскостей проекций (проецированием на дополнительную плоскость), приведенными в предыдущем параграфе.
Рассмотрим построение разверток поверхности некоторых простейших тел.
Подобным образом можно построить развертки прямых призм с любой фигурой в основании.
Развертка поверхности прямого кругового конуса представляет собой плоскую фигуру, состоящую из кругового сектора и круга (рис. 176, в). Построение выполняют следующим образом. Проводят осевую линию и из точки, взятой на ней, как из центра, радиусом Rh равным образующей конуса sfd, очерчивают дугу окружности. В данном примере образующая, подсчитанная по теореме Пифагора, равна приблизительно
38 мм (L = √l5 2 + 35 2 = √l450 ≈ % 38 мм). Затем подсчитывают угол сектора по формуле
В данном примере α = 360°⋅15/38 ≈ 142,2°.
Этот угол строят симметрично относительно осевой линии с вершиной в точке s. К полученному сектору пристраивают круг с центром на осевой линии и диаметром, равным диаметру основания конуса.
Рис. 176. Чертеж разверток поверхностей геометрических тел
Урок черчения: «Чертежи развёрток некоторых геометрических тел»
Конспект урока черчения.
Тема: Чертежи разверток некоторых геометрических тел.
— закрепить понятие геометрические тела;
— читать и строить их чертежи геометрических тел;
— способствовать самостоятельному изучению построению разверток геометрических тел;
— развивать пространственные представления и мышление, умение работать с информационными источниками;
— воспитывать чувство времени, ответственности в коллективе.
Тип урока: урок изучения нового материала
Очень правильно, очень мудро,
Да не будет помехой лень,
Утром говорить всем: «Доброе … ( утро)»,
Ну а днем говорить: «Добрый..( день)».
Просмотр готовности учащихся к уроку.
Готов ли ты начать урок!
Всё ли на месте? Всё ли в порядке:
Книжки, ручки, карандаши и тетрадки?
Есть у нас девиз такой:
Всё, что надо под рукой!
2. Актуализация знаний
На прошлых уроках мы рассмотрели некоторые геометрические тела, научились строить их чертежи. Давайте вспомним, какие геометрические тела бывают?
Я показываю, а учащиеся называют.
Давайте проверим, как вы усвоили пройденный материал.
Каков порядок расположения проекций? (фронтальная, горизонтальная и профильная).
Один работает у доски (Юра), выполняя проекции конуса, а остальные работают самостоятельно в своих тетрадях.
Высота конуса L= 40 мм, а диаметр основания 30 мм.
3. Изучение нового материала.
Сообщение темы урока.
Сегодня мы продолжим работу с геометрическими телами, тема сегодняшнего урока: «Чертежи разверток некоторых геометрических тел».
На уроке мы должны научиться самостоятельно, выполнять развёртку некоторых геометрических тел.
С развёртками поверхностей мы часто встречаемся в обыденной жизни, на производстве, в строительстве. Чтобы изготовить упаковку для сока, конфет, духов, праздничную коробочку или кулёк и т.п., надо уметь строить развёртки поверхностей геометрических тел.
Рассмотрите развёртки упаковок и скажите, из каких геометрических фигур они состоят?
А что же такое развёртка? Откроем учебники на странице 63 и прочитаем определение.
А теперь я покажу вам порядок выполнения развёртки некоторых геометрических тел.
Развёртка поверхности пирамиды.
Для того чтобы выполнить развёртку, давайте определим из каких фигур состоит пирамида.
Боковая поверхность пирамиды состоит из четырех равных треугольников. Для построения треугольника необходимо знать величины его сторон. Равные ребра пирамиды служат боковыми сторонами граней (треугольниками). Из произвольной точки описываем дугу радиусом, равным длине бокового ребра пирамиды. На этой дуге откладываем четыре отрезка, равные стороне основания. Крайние точки соединяем прямыми с центром описанной дуги. Затем пристраиваем квадрат, равный основанию пирамиды.
Развёртка поверхностей цилиндра.
Развёртка боковой поверхности цилиндра состоит из прямоугольника и двух кругов. Одна сторона прямоугольника равна высоте цилиндра, другая – длине окружности основания.
Длина окружности высчитывается по формуле: L= Пи*D.
На чертеже развёртки к прямоугольнику пристраивают два круга, диаметр которых равен диаметру основания цилиндра.
Линии сгиба должны проводиться штрихпунктирной линией с двумя точками.
Всё понятно? Для закрепления нового материала выполним по карточкам практическую работу в парах. А один у доски выполнит развёртку куба.
4. Практическая работа в парах. Прежде чем начать работу, скажите, пожалуйста, с какими инструментами и с каким материалом вы будете работать?
Чертежи детали
Рабочие чертежи разрабатывают, как правило, на все детали, входящие в состав изделия.
Допускается не выпускать чертежи на:
а) детали, изготовляемые из фасонного или сортового материала отрезкой под прямым углом, из листового материала отрезкой по окружности в том числе, с концентрическим отверстием или по периметру прямоугольника без последующей обработки;
б) одну из деталей изделия в случаях, указанных в требованиях к выполнение отдельных видов сборочных чертежей.
в) детали изделий с неразъемными соединениями (сварных, паяных, клепаных, склеенных, сбитых гвоздями и т. п.), являющихся составными частями изделий единичного производства, если конструкция такой детали настолько проста, что для ее изготовления достаточно трех-четырех размеров на сборочном чертеже или одного изображения такой детали на свободном поле чертежа;
г) детали изделий единичного производства, форма и размеры которых (длина, радиус сгиба и т. п.) устанавливаются по месту, например, отдельные части ограждений и настила, отдельные листы обшивки каркасов и переборок, полосы, угольники, доски и бруски, трубы и т. п.;
д) покупные детали, подвергаемые антикоррозионному или декоративному покрытию, не изменяющему характер сопряжения со смежными деталями.
Необходимые данные для изготовления и контроля деталей, на которые не выпускают чертежи, указывают на сборочных чертежах и в спецификации.
На чертежах деталей и в спецификации условные обозначения материала должны соответствовать обозначениям, установленным стандартами на материал. При отсутствии стандарта на материал его обозначают по техническим условиям.
Обозначение материала детали по стандарту на сортамент записывают на чертеже только в тех случаях, когда деталь в зависимости от предъявляемых к ней конструктивных и эксплуатационных требований должна быть изготовлена из сортового материала определенного профиля и размера, например:
40 ГОСТ 1133-71
| Ст3 ГОСТ 535-88 |
Допускается в условном обозначении материала не указывать группу точности, плоскостность, вытяжку, обрезку кромок, длину и ширину листа, ширину ленты и другие параметры, если они не влияют на эксплуатационные качества изделия (детали). При этом общая последовательность записи данных, установленных стандартами или техническими условиями на материалы, должна сохраняться.
В основной надписи чертежа детали указывают не более одного вида материала. Если для изготовления детали предусматривается использование заменителей материала, то их указывают в технических требованиях чертежа или технических условиях на изделие.
Если форма и размеры всех элементов определены на чертеже готовой детали, развертку (изображение, длину развертки) не приводят.
Когда изображение детали, изготовляемой гибкой, не дает представления о действительной форме и размерах отдельных ее элементов, на чертеже детали помещают частичную или полную ее развертку. На изображении развертки наносят только те размеры, которые невозможно указать на изображении готовой детали.
Над изображением развертки помещают знак 
(рис. 21).
Развертку изображают сплошными основными линиями, толщина которых должна быть равна толщине линий видимого контура на изображении детали.
Рисунок 21. Чертеж детали изготовленной гибкой
При необходимости, на изображении развертки наносят линии сгибов, выполняемые штрихпунктирной тонкой линией с двумя, с указанием на полке линии-выноски «Линия сгиба».
Допускается, не нарушая ясности чертежа, совмещать изображение части развертки с видом детали. В этом случае развертку изображают штрихпунктирными тонкими линиями с двумя точками и знак не помещают (рис. 22).
Рисунок 22. Пример совмещения развертки с видом детали
Рисунок 23. Чертеж пружины
Если у такой детали деформируемые элементы в свободном состоянии могут иметь произвольную форму, то деталь изображают на чертеже в состоянии ее измерения с соответствующим указанием на поле чертежа (рис. 24).
Рисунок 24. Пример чертежа детали, деформируемые элементы которой в свободном положении могут иметь произвольную форму
Если деталь должна быть изготовлена из материала, имеющего определенное направление волокон, основы и т. п. (металлическая лента, ткани, бумага, дерево), то на чертеже при необходимости допускается указывать направление волокон (рис. 25).
Рисунок 25. Примеры указания направления волокон, основы и т.д.
Указания о расположении слоев материала детали, изготовляемой из текстолита, фибры, гетинакса или другого слоистого материала, при необходимости помещают в технических требованиях (рис. 26).
Рисунок 26. Пример указания расположения слоев материала детали
На чертежах деталей, изготовляемых из материалов, имеющую лицевую и оборотную стороны (кожа, некоторые виды тканей, пленок и др.), при необходимости на полке линии-выноски указывают лицевую сторону (рис. 27). Такие указания допускается помещать и на сборочных чертежах изделий, в состав которых входят детали, имеющие лицевую и оборотную сторону (рис. 28).
Рисунок 27. Пример указания лицевой стороны детали
Детали из прозрачных материалов изображают как непрозрачные. Нанесенные на детали с обратной стороны от наблюдателя надписи, цифры, знаки и другие подобные данные, которые у готовой детали должны быть видны с лицевой стороны, изображают на чертеже как видимые и помещают соответствующее указание в технических требованиях (рис. 29).
Развёртывание поверхностей
Содержание:
Развертывание цилиндров и конусов основывается на способах развертки гранных поверхностей приведенных выше. В общем случае поверхность цилиндра аппроксимируется призматической поверхностью, а конус – пирамидой и затем строится приближенная развертка кривой поверхности.
Свойства развёрток
Развёрткой криволинейной поверхности Ф называется плоская фигура 
, полученная путём совмещения поверхности Ф с плоскостью Σ (рис. 5.1). В начертательной геометрии плоскостью Σ является одна из плоскостей проекций.
Развёртывание поверхности
Применение развёрток
Поверхности Ф, которые можно совместить с плоскостью Σ без разрывов и складок, являются, развёртывающимися. К ним принадлежат все многогранники (см. п. 4.1), цилиндрические и конические поверхности (см. п. 3.2.1.3, рис. 3.55 б – в), торсы (см. п. 3.2.1.3, рис. 3.57). Все другие кривые поверхности не развёртываются на плоскость, поэтому при их изготовлении из листового материала они приближённо заменяются развёртывающимися поверхностями (призмами, пирамидами, цилиндрами, конусами). В этих случаях имеют место так называемые условные развёртки (см. п. 5.4.1.3 – 5.4.1.4).
Основные свойства развёрток:
а) прямая l на поверхности Ф отвечает прямой 
на развёртке 
б) параллельные прямые 
на поверхности Ф отвечают параллельным прямым 
на развёртке 
в) длина (натуральная величина) любой линии s на поверхности Ф равна длине линии 
на развёртке 
г) угол α между линиями r, s на поверхности Ф равен углу между линиями 
на развёртке
д) площадь S фигуры на поверхности Ф равна плоскости соответствующей фигуры на развёртке 
е) если прямая на развёртке 
отвечает кривой линии s на поверхности Ф, то кривая s является геодезическою линией поверхности Ф. Длина дуги МN геодезической линии является наименьшей из всех возможных дуг MN на поверхности Ф.
Описанные свойства геометрически интерпретированы на рис. 5.3.
Свойства развёрток
Геодезическая линия широко применяется в неэвклидовой геометрии, теоретических и практических задачах геодезии – науки, которая изучает измерения пространства, в том числе размеры и форму Земли, её гравитационное поле и т.д.
Развёртывание поверхности многогранника
Развёрткой многогранника называется фигура, полученная в результате последовательного совмещения граней многогранника с плоскостью. Развёртка всегда строится наружной (лицевой) стороной к наблюдателю.
Способ натуральных граней
Согласно свойствам развёртки (см. п. 5.1) все грани многогранника Ф сохраняют на развёртке свою длину, для определения которой используются способы начертательной геометрии.
На рис. 5.4 построены горизонтальная и фронтальная проекции треугольной пирамиды SABC. Основа АВС является плоскостью горизонтального уровня, поэтому проецируется на П1 в натуральную величину А1В1С1. Для определения натуральных величин граней SAB, SBC, SCA используется способ вращения вокруг горизонтально-проецирующей оси і, которая проходит через вершину S пирамиды. Отрезки 
являются натуральными величинами ребер SA, SB, SC пирамиды. По этим ребрам строится развёртка пирамиды. Вырезав плоскую заготовку из контура развёртки и сложив её по линиям сгиба и совмещая одноименные рёбра, можно получить поверхность данной пирамиды SABC.
Способ натуральных граней
Для определения на развёртке произвольной точки D пирамиды применяется способ вспомогательного отрезка. Точка D принадлежит грани SАС. Через вершину S и точку D проводится отрезок S-1, точка 1 которого принадлежит основе АВС пирамиды. Определяется натуральная величина 
отрезка S-1, на нём определяется проекция 
На отрезке 
развёртки строится отрезок 
, длина которого равна длине проекции 
Способ нормального сечения
Способ нормального сечения применяется для построения развёртки призм, ребра которых являются прямыми уровня.
Суть способа нормального сечения
Призма пересекается в произвольном месте плоскостью Σ, перпендикулярной рёбрам. Определяется натуральная величина линии 1 – 2 – … нормального сечения. Эта линия является плоским многоугольником, количество сторон которого равно количеству граней призмы. Линия 1 – 2 – … разворачивается до формы прямого отрезка 
… На перпендикулярах, проведенных по обе стороны от точек 
…, строятся части натуральных величин рёбер пирамиды, которые находятся по разные стороны секущей плоскости Σ.
На рис. 5.5 заданы две проекции треугольной призмы ABCDEF с рёбрами AD, BE, CF горизонтального уровня. Вводится секущая плоскость Σ, перпендикулярная рёбрам призмы (горизонтальный след Σ1 перпендикулярен горизонтальным проекциям рёбер призмы). Плоскость Σ пересекает призму по треугольнику 1 – 2 – 3, точки которого принадлежат, соответственно, рёбрам AD, BE, CF. Способом замены плоскостей проекций определяется натуральная величина 
нормального сечения (ось 
параллельна следу Σ1). Треугольник 
разворачивается до формы прямого отрезка 
длины частей 
которого равны соответствующим сторонам треугольника 
На перпендикулярах, проведенных по обе стороны от точек 
строятся отрезки 
длины которых равны длинам проекций 
На развёртке достраиваются натуральные величины основ АВС, DEF призмы.
Способ нормального сечения
Для определения на развёртке произвольной точки G призмы применяется способ вспомогательных отрезков. Точка G принадлежит грани ABDE. Через точку G проводится отрезок 4 – 5, параллельный рёбрам призмы. Точка 4 принадлежит отрезку АВ, точка 5 – отрезку DE. Определяется точка 6 пересечения отрезка 4 – 5 с плоскостью Σ. Точка 6 принадлежит отрезку 1 – 2. Определяется проекция 
На отрезке 
развёртки строится отрезок 
, длина которого равна длине проекции 
Из точки 
развёртки призмы проводится отрезок 
в направлении, перпендикулярном отрезку 
в сторону точки 
Длина отрезка 
равна длине проекции 
Способ раскатки
Способ раскатки применяется для развёртывания призмы, основа которой параллельна одной плоскости проекций, а боковые рёбра параллельны другой плоскости проекций.
Из точек 1, 2, … основы 
… верхней грани призмы проводятся лучи, перпендикулярные боковым рёбрам 
… На этих лучах строятся точки 
… так, что длины отрезков 
… равны натуральным величинам отрезков 
, …
На рис. 5.6 заданы две проекции треугольной призмы 
с основой 1 – 2 – 3 и верхней гранью 
горизонтального уровня и рёбрами 
фронтального уровня. Из фронтальных проекций 
проводятся лучи, перпендикулярные фронтальным проекциям 
На этих лучах по очереди откладываются точки 
так, что длины отрезков 
равны натуральным величинам отрезков
Способ раскатки
Для определения на развёртке произвольной точки А призмы применяется способ вспомогательного луча. Точка А принадлежит грани 
Через точку А проводится отрезок 
параллельный рёбрам призмы, точка 4 которого принадлежит отрезку 1 – 3 основы. Из проекций 
проводятся лучи 
перпендикулярные фронтальным проекциям рёбер призмы. Из точки 
принадлежащей отрезку 
развёртки, проводится отрезок 
параллельный отрезку 
до пересечения с лучом 
Развёртывание поверхностей тел вращения
По развертыванию поверхности делятся на два класса: развертываемые, которые можно совместить с плоскостью без разрывов и складок, и неразвертываемые, которые невозможно совместить с плоскостью без разрывов и складок. Развертываются все многогранные поверхности, из кривых поверхностей – только линейчатые, у которых смежные образующие параллельны между собой (цилиндрические) или пересекаются по одной точке (конические).
Из всего разнообразия поверхностей тел вращения точное развёртывание осуществляется только для прямых круговых цилиндра и конуса (рис. 5.7 – 5.8).
Поверхность прямого кругового цилиндра разворачивается в прямоугольник, одна сторона которого равна длине 
нормального сечения (окружности диаметром d), другая – высоте h цилиндра (рис. 5.7). Развёртка цилиндра при необходимости дополняется нижней и верхней основами – окружностями диаметром d. Для определения точки А на развёртке прямого кругового цилиндра применяется способ образующей линии. Определяется угол α, и строится образующая линия на развёртке. Она размещена на расстоянии 
Высота точки 
равна высоте точки А.
Развёртка цилиндра
Поверхность прямого кругового конуса разворачивается в сектор окружности с центром в вершине S конуса. Радиус сектора равен длине l образующей линии конуса; угол φ = 180°·d/l, где d – диаметр основы конуса (рис. 5.8). Развёртка конуса при необходимости дополняется основой – окружностью диаметром d. Для определения точки А на развёртке прямого кругового конуса применяется способ образующей линии. Определяется угол α и строится образующая линия на развёртке, положение которой определяется углом β = 0,5αd/l. Точка 
расположена на расстоянии 
равном натуральной величине 
отрезка SA.
Развёртка конуса
Приближённое и условное развёртывание кривых поверхностей
При построении приближенных и условных разверток используют ап-проксимацию (от approximare (лат.) – приближаться) одной поверхности к другой. Аппроксимацией называют замену одной поверхности другой – аппроксимирующей, которая приближается к заданной по каким-то опре-деленным свойствам (форма, площадь, кривизна) с той или иной степенью точности.
Способ аппроксимирующих поверхностей
Развёртка любой развёртывающейся поверхности (кроме прямых круговых конуса и цилиндра) строится приближённо. Это происходит вследствие того, что при развёртывании кривой поверхности её аппроксимируют гранями вписанных многогранников(рис. 5.9).
Способ призматических поверхностей
Например, цилиндрическая поверхность условно заменяется призмой (рис. 5.9 а), коническая поверхность – пирамидой (рис. 5.9 б).
– Аппроксимация тела вращения многогранником
Для построения приближённой развёртки цилиндрической поверхности используется способ призматических поверхностей
Суть способа призматических поверхностей
В цилиндрическую поверхность вписывается призма, количество граней которой прямо влияет на точность построения развёртки цилиндра. Строится развёртка этой призмы способом нормального сечения или раскатки (см. п. 5.2.2 – 5.2.3). Через точки на развёртке призмы проводятся плавные кривые, являющиеся контуром приближённой развёртки цилиндра. При необходимости развёртка цилиндра дополняется нижней и верхней основами.
На рис. 5.10 изображен комплексный чертёж эллиптического цилиндра, поверхность которого аппроксимируется двенадцатигранной призмой. Развёртка последней строится способом раскатки. Через точки 
проводятся плавные кривые (синусоиды), образующие контур развёртки цилиндра. Развёртка дополняется нижней и верхней основами цилиндра.
Способ пирамидальных поверхностей
Способ пирамидальных поверхностей используется для построения развёртки боковой поверхности конуса.
Суть способа пирамидальных поверхностей
В коническую поверхность вписывается пирамида. Строится приближённая развёртка этой пирамиды способом натуральных граней (см. п. 5.2.1). Через точки на развёртке пирамиды проводится плавная кривая, являющаяся контуром развёртки конуса. По необходимости развёртка конуса дополняется его основой.
Аппроксимация (от англ. approximation – приближение) – научный метод, состоящий в замене одних объектов другими, более простыми, приближёнными к оригиналу.
Необходимо различать такие понятия, как приближённая и условная развёртка. Приближённая развёртка касается развёртывающихся поверхностей. Условная развёртка строится для поверхностей, которые не развёртываются.
Развёртка эллиптического цилиндра
На рис. 5.11 изображен комплексный чертёж эллиптического конуса, поверхность которого аппроксимируется двенадцатигранной пирамидой. Развёртка последней строится способом натуральных граней. Через точки 
проводится плавная кривая, которая образует контур развёртки конуса. Развёртка дополняется основой конуса.
Развёртка эллиптического конуса
Способ цилиндрических поверхностей
Для поверхностей, которые не развёртываются. в том числе нелинейчатых, строятся условные развёртки. Основные способы построения условных развёрток такие:
а) способ цилиндрических поверхностей;
б) способ конических поверхностей;
в) метод триангуляции.
Суть способа цилиндрических поверхностей
Кривая поверхность описывается совокупностью цилиндрических поверхностей, которые в дальнейшем развёртываются и совмещаются по точкам и линиям. Полученная развёртка является условной развёрткой кривой поверхности.
На рис. 5.12 построена условная развёртка сферы. Вокруг её поверхности описываются шесть одинаковых цилиндрических поверхностей. Одна из таких поверхностей имеет образующие линии 
Длины этих образующих равны длинам их горизонтальных проекций 
.Расстояния между образующими одинаковы и равны длине дуги SA, то есть длине фронтальной проекции 
Развёрткой одной из шести цилиндрических поверхностей является фигура в форме лепестка, контур которой проходит через концы 
образующих линий, удалённых одна от другой на одинаковое расстояние, равное длине дуги . Прибавляя к полученной части еще пять, строится условная развёртка сферы.
Условная развёртка сферы.
На рис. 5.13 построена условная развёртка открытого тора. Вокруг его поверхности описываются двенадцать одинаковых цилиндрических поверхностей. Одна из таких поверхностей имеет образующие линии 
Длины этих образующих равны длинам их фронтальных проекций 
Расстояния между образующими одинаковы и равны длине дуги SA, то есть, длине горизонтальной проекции S1A1. Развёрткой одной из двенадцати цилиндрических поверхностей является фигура, контур которой проходит через концы 
образующих линий, удалённых одна от другой на одинаковое расстояние, равное длине дуги S1A1. Прибавляя к полученной части еще одиннадцать, строится условная развёртка тора.
Условная развёртка открытого тора
Способ конических поверхностей
Способ конических поверхностей используется для построения условных развёрток закрытых тел вращения (эллипс, параболоид, эллипсоид, двуполостной гиперболоид, закрытый тор и т.д.).
Суть способа конических поверхностей
Сегменты поверхности описываются совокупностью конических поверхностей, которые развёртываются и совмещаются по точкам и линиям. Полученная развёртка является условной развёрткой кривой поверхности.
На рис. 5.14 построена условная развёртка сферы. Вокруг её поверхности описывается одна цилиндрическая и шесть конических поверхностей с разными вершинами 
Длины образующих линий 
одинаковы и равны длине проекции 
Углы и радиусы развёртывания конусов определяются, как описано в п. 5.3.
Условная развёртка сферы
На рис. 5.15 построена условная развёртка эллипсоида. Вокруг его поверхности описываются одна цилиндрическая и шесть конических поверхностей с разными вершинами 
Длины образующих линий 
могут быть разными и определяются по их фронтальным проекциям. Углы и радиусы развёртывания конусов определяются, как показано в п. 5.3.
Условная развёртка эллипсоида
Метод триангуляции
Метод триангуляции (от англ. triangle – треугольник) применяется для развёртывания многогранников, приближенного развёртывания цилиндрических и конических поверхностей и поверхностей с ребром поворота (торсов), а также условного развёртывания поверхностей которые не развёртываются.
Суть метода триангуляции
Кривая поверхность разбивается на треугольники с общими сторонами. Натуральные величины этих треугольников сочетаются по общим сторонам. Внешний контур полученной плоской фигуры является приближенной или условной развёрткой заданной кривой поверхности.
На рис. 5.16 построена приближённая развёртка торса Ф. Последний разбивается совокупностью треугольников с вершинами 1, 2, …, принадлежащими ребру возврата 
и одной из линий l поверхности Ф. Натуральные величины сторон 1 – 2, 2 – 3, … треугольников определяются способом вращения вокруг проецирующей оси. По найденным отрезкам строятся натуральные величины треугольников 1 – 2 – 3, 2 – 3 – 4, …, которые сочетаются по общим сторонам. Контур полученной плоской фигуры является приближенной развёрткой торса Ф.
Приближённая развёртка торса
На рис. 5.17 построена приближённая развёртка поверхности произвольного пространственного тела. Его поверхность разбивается на треугольники, стороны которых построены по точкам 1, 2, …, А, В, …, принадлежащим соответственно верхней и нижней основам тела. Натуральные величины сторон треугольников определяются способом вращения вокруг горизонтально-проецирующих осей, проходящих через точки В, С. По найденным отрезкам строятся натуральные величины треугольников, которые сочетаются по общим сторонам. Контур полученной плоской фигуры является приближенной развёрткой поверхности тела.
Развёртка поверхности тела методом триангуляции
Примеры и образцы решения задач:
Услуги по выполнению чертежей:
Присылайте задания в любое время дня и ночи в ➔ 
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.