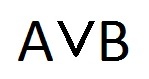какой знак используется для записи дизъюнкции
Урок на тему «Логические операции. Дизъюнкция»
Следующая логическая операция, которую мы рассмотрим после конъюнкции — дизъюнкция. Часто можно встретить другие названия этой операции — логическое сложение, логическое ИЛИ или просто ИЛИ.
В естественном языке дизъюнкция заменяется союзом ИЛИ.
Дизъюнкция, как и конъюнкция — бинарная операция, т. е. для нее необходимо два операнда.
Рассмотрим пример. Пусть есть два высказывания: A = «Париж — столица Франции» и B = «Сегодня пасмурно«. Тогда дизъюнкция этих высказываний будет выглядеть так «Париж — столица Франции ИЛИ сегодня пасмурно «, а обозначаться так:
Так как на клавиатуре нет символа дизъюнкция, его можно набрать из бэкслэша ( \ ) и слэша ( / ) — получится \/ — похоже на обозначение дизъюнкции.
Таблица истинности для дизъюнкции выглядит так:
| A | B | A \/ B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
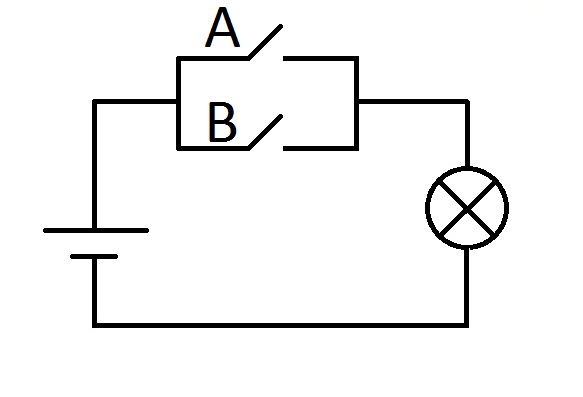
Запомнить таблицу довольно просто — дизъюнкция ложна только в одном случае — когда оба исходных высказывания ложны. Так же можно запомнить таблицу истинности для дизъюнкции, если представить ее электрический аналог — два параллельно включенных выключателя:
Электрический аналог дизъюнкции
По схеме сразу понятно, что лампочка будет гореть когда замкнуты оба выключателя, либо хотя бы один из них — аналогично дизъюнкции.
Автор: Александр Чернышов
Оцените статью, это очень поможет развитию сайта.
Дизъюнкция
Логическая операция Дизъюнкция — бинарная операция над высказываниями, результатом которой является истинное высказывание в случаях, когда среди исходных высказываний есть хотя бы одно истинное. Дизъюнкция ложна, если оба исходных высказывания ложны.
Другие названия дизъюнкции — логическое сложение, логическое ИЛИ или просто ИЛИ.
Дизъюнкция изучается в информатике при рассмотрении раздела алгебра логики.
В естественных языках дизъюнкцию заменяют союзом «или«.
В языках программирования для дизъюнкции используют обозначение ‘ or ‘ или одинарной (двойной) вертикальной чертной ‘ | ‘ (либо ‘ || ‘) (например, x 5 или a>=10 || a ).
Как набрать знак дизъюнкцию на клавиатуре
Так как на клавиатуре нет знака дизъюнкции (∨), ее удобно набирать используя комбинацию символов обратный слэш и слэш \/.
Таблица истинности для дизъюнкции
Истинность дизъюнкции определяется ее таблицей истинности.
| A | B | A \/ B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Дизъюнкция и круги Эйлера
Результатом дизъюнкции является как область пересечения высказываний, там и области самих исходных высказываний.
Электрический аналог дизъюнкции
Представим, что выключатели A и B — это высказывания, причем 0 — выключатель разомкнут, 1 — выключатель замкнут. Лампа символизирует дизъюнкцию. Когда она не горит — 0, горящая лампа — 1. Тогда становится очевидным, что лампа будет гореть если хотя бы один (и оба сразу) выключатель будет замкнут, что полностью соотносится с таблицей истинности для дизъюнкции.
Какой знак используется для записи дизъюнкции
2) Логическое сложение или дизъюнкция:
Таблица истинности для дизъюнкции
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
3) Логическое отрицание или инверсия:
Таблица истинности для инверсии
| A | ¬ А |
| 1 | 0 |
| 0 | 1 |
4) Логическое следование или импликация:
«A → B» истинно, если из А может следовать B.
Обозначение: F = A → B.
Таблица истинности для импликации
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
5) Логическая равнозначность или эквивалентность:
Какой знак используется для записи дизъюнкции
§ 2. Логические операции. Формализация высказываний
Сейчас мы познакомимся с шестью основными логическими операциями. Каждая из них имеет несколько названий и обозначений.
Названия операции
Возможные обозначения
Конъюнкция, логическое умножение, операция И, операция AND.
`&, ^^, *,` по аналогии с алгебраическим умножением может никак не обозначаться
Дизъюнкция, нестрогая дизъюнкция, логическое сложение, операция ИЛИ, операция OR.
Строгая дизъюнкция, разделительная дизъюнкция, исключающее ИЛИ, сложение по модулю `2`.
Эквивалентность, эквиваленция, равенство, равнозначность.
Импликация, следование, следствие
Теперь для того чтобы строго определить эти логические операции, нам нужно для каждой из них выписать таблицу истинности. Все перечисленные операции кроме отрицания имеют два операнда. Знак операции в выражениях пишется между операндами (как в алгебре чисел). Операция отрицания имеет один операнд и в выражениях записывается либо в виде черты над операндом, либо в виде символа «приставка» слева от операнда.
1) `p` и `q` ложны. Это значит, что четырёхугольник не является квадратом и его стороны не равны. Это возможная ситуация.
2) `p` – ложно, `q` – истинно. Это значит, что четырёхугольник не является квадратом, но стороны у него равны. Это возможно (ромб).
3) `p` – истинно, `q` – истинно. Это значит, что четырёхугольник является квадратом и стороны у него равны. Это возможная ситуация.
4) `p` – истинно, `q` – ложно. Это значит, что четырёхугольник является квадратом, но стороны у него не равны. Это невозможная ситуация.
Очень часто вместо «присвоим логическим переменным эти высказывания» говорят «обозначим высказывания следующим образом». В дальнейшем мы тоже будем использовать этот речевой оборот.
Логика
НЕКОТОРЫЕ
СВОЙСТВА ЛОГИЧЕСКИХ ОПЕРАЦИЙ
1. Обозначения
1.1. Обозначения для логических связок (операций):
a) отрицание (инверсия, логическое НЕ) обозначается ¬ (например, ¬А);
b) конъюнкция (логическое умножение, логическое И) обозначается /\
(например, А /\ В) либо & (например, А & В);
c) дизъюнкция (логическое сложение, логическое ИЛИ) обозначается \/
(например, А \/ В);
d) следование (импликация) обозначается → (например, А → В);
e) тождество обозначается ≡ (например, A ≡ B). Выражение A ≡ B истинно тогда и только тогда, когда значения A и B совпадают (либо они оба истинны, либо они оба ложны);
f) символ 1 используется для обозначения истины (истинного высказывания); символ 0 – для обозначения лжи (ложного высказывания).
1.2. Два логических выражения, содержащих переменные, называются равносильными (эквивалентными), если значения этих выражений совпадают при любых значениях переменных. Так, выражения А → В и (¬А) \/ В равносильны, а А /\ В и А \/ В – нет (значения выражений разные, например, при А = 1, В = 0).
1.3. Приоритеты логических операций: инверсия (отрицание), конъюнкция (логическое умножение), дизъюнкция (логическое сложение), импликация (следование), тождество. Таким образом, ¬А \/ В \/ С \/ D означает то же, что и
Возможна запись А \/ В \/ С вместо (А \/ В) \/ С. То же относится и к конъюнкции: возможна запись А /\ В /\ С вместо (А /\ В) /\ С.
2. Свойства
Приведенный ниже список НЕ претендует на полноту, но, надеемся, достаточно представителен.
2.1. Общие свойства
2.2.Дизъюнкция
2.3. Конъюнкция
2.4. Простые дизъюнкции и конъюнкции
Назовем (для удобства) конъюнкцию простой, если подвыражения, к которым применяется конъюнкция, – различные переменные или их отрицания. Аналогично, дизъюнкция называется простой, если подвыражения, к которым применяется дизъюнкция, – различные переменные или их отрицания.
2.5. Импликация