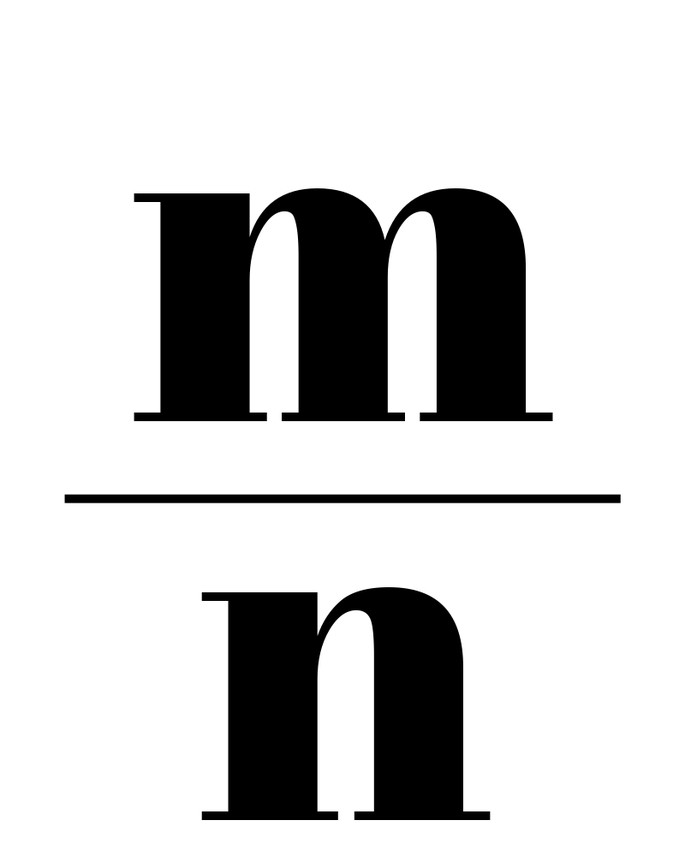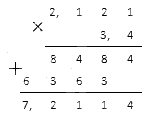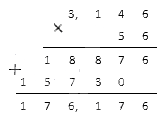при каком условии равно нулю произведение рациональных чисел частное рациональных чисел
Что такое Рациональные числа?
Определение рациональных чисел
Рациональное число — это число, которое можно представить в виде положительной или отрицательной обыкновенной дроби или числа ноль. Если число можно получить делением двух целых чисел, то это число рациональное.
Рациональные числа — это те, которые можно представить в виде
где числитель m — целое число, а знаменатель n — натуральное число.
Рациональные числа – это все натуральные, целые числа, обыкновенные дроби, бесконечные периодические дроби и конечные десятичные дроби.
Множество рациональных чисел принято обозначать латинской буквой Q.
Примеры рациональных чисел:
Свойства рациональных чисел
У рациональных чисел есть определенные законы и ряд свойств — рассмотрим каждый их них. Пусть а, b и c — любые рациональные числа.
Кроме основных перечисленных есть еще ряд свойств:
Мы знаем, что 0 = d + (-d) для любого рационального d, значит a * 0 = a * (d + (-d)).
Распределительный закон позволяет переписать выражение:
Так получилась сумма двух противоположных чисел, которая в результате дает нуль, что доказывает равенство a * 0 = 0.
Определение иррационального числа
Иррациональное число — это действительное число, которое невозможно выразить в форме деления двух целых чисел, то есть в рациональной дроби
Оно может быть выражено в форме бесконечной непериодической десятичной дроби.
Бесконечная периодическая десятичная дробь — это такая дробь, десятичные знаки которой повторяются в виде группы цифр или одного и того же числа.
Обозначение множества иррациональных чисел: латинская буква I.
Действительные или вещественные числа — это все рациональные и иррациональные числа: положительные, отрицательные и нуль.
Свойства иррациональных чисел:
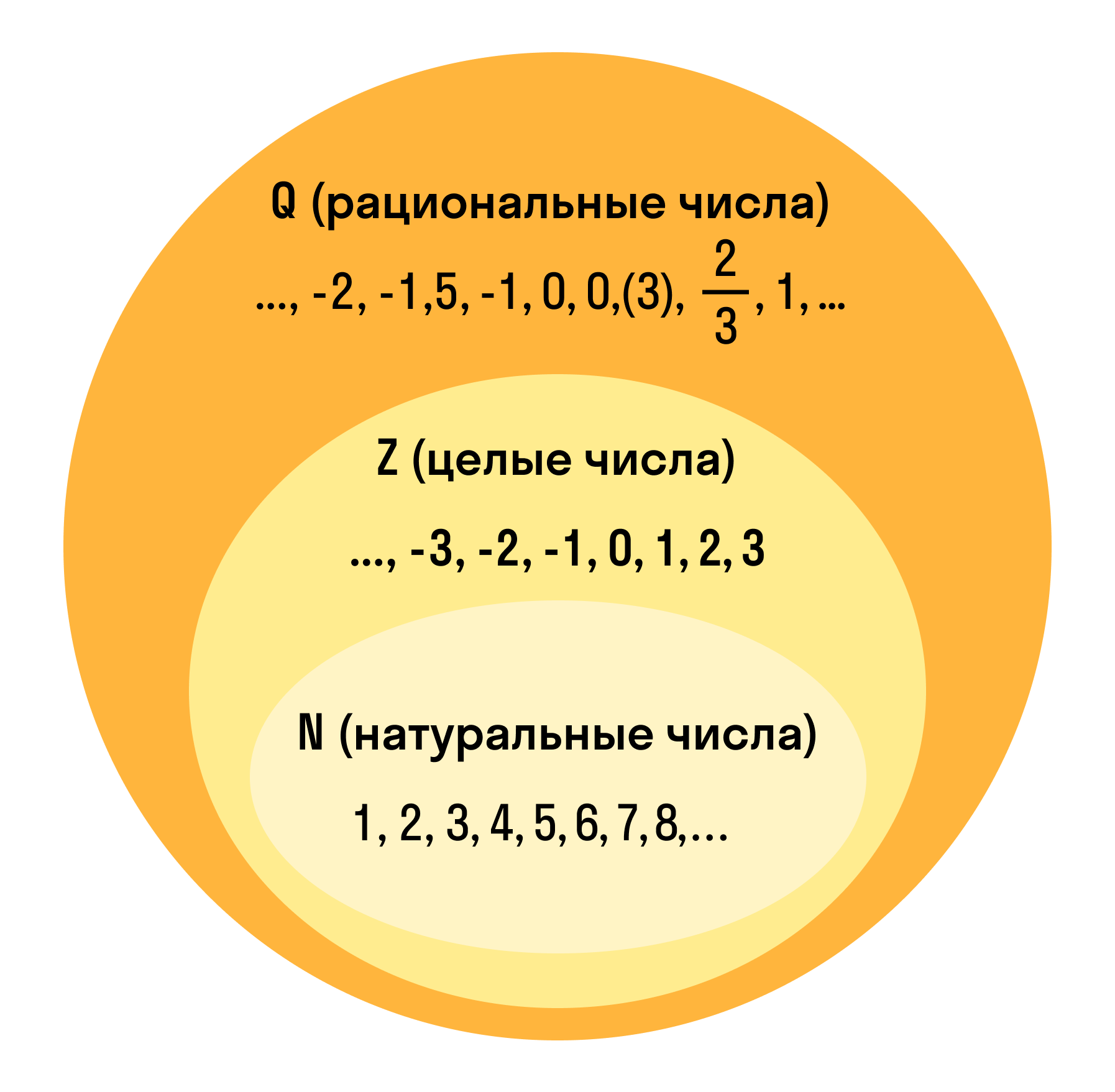
Различие между целыми, натуральными и рациональными числами
Натуральные числа — это числа, которые мы используем, чтобы посчитать что-то конкретное, осязаемое: один банан, две тетрадки, десять стульев.
А вот, что точно не является натуральным числом:
Целые числа — это натуральные числа, противоположные им и нуль.
Какие числа называются рациональными мы уже знаем из первой части статьи. Повторим еще раз.
Рациональные числа — это конечные дроби и бесконечные периодические дроби.
Например:
Любое рациональное число можно представить в виде дроби, у которой числитель принадлежит целым числам, а знаменатель — натуральным. Поэтому во множество рациональных чисел входит множество целых и натуральных чисел.
Но не все числа можно назвать рациональными. Например, бесконечные непериодические дроби не принадлежат множеству рациональных чисел. Так √3 или 𝜋 (число пи) нельзя назвать рациональными числами.
Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)
Записаться на марафон
Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)
Рациональные числа: определения, примеры
Данная статья посвящена изучению темы «Рациональные числа». Ниже приведены определения рациональных чисел, даны примеры, рассказано о том, как определить, является ли число рациональным, или нет.
Рациональные числа. Определения
Прежде чем дать дефиницию рациональных чисел вспомним, какие еще есть множества чисел, и как они связаны между собой.
Натуральные числа, в совокупности с противоположными им и числом ноль образуют множество целых чисел. В свою очередь, совокупность целых дробных чисел образует множество рациональных чисел.
Определение 1. Рациональные числа
Таким образом, можно оставить ряд свойств рациональных чисел:
Приведенное выше определение рациональных чисел можно сформулировать более кратко. Еще раз ответим на вопрос, что такое рациональное число.
Определение 2. Рациональные числа
Можно показать, что данное определение равносильно предыдущему определению рациональных чисел. Чтобы сделать это, вспомним, что черта дроби равносильна знаку деления. С учетом правил и свойств деления целых чисел, можно записать следующие справедливые неравенства:
Таким образом, можно записать:
Приведем еще одну эквивалентную форму определения рациональных чисел.
Определение 3. Рациональные числа
Данное определение напрямую следует из самого первого определения этого пункта.
Подведем итог и сформулируем резюме по данному пункту:
Какое из чисел является рациональным?
Как мы уже выяснили, любое натуральное число, целое число, правильная и неправильная обыкновенная дробь, периодическая и конечная десятичная дробь являются рациональными числами. Вооружившись этими знаниями можно без труда определить, является ли какое-то число рациональным.
Однако на практике часто приходится иметь дело не с числами, а с числовыми выражениями, которые содержат корни, степени и логарифмы. В некоторых случаях ответ на вопрос «рационально ли число?» является далеко не очевидным. Рассмотрим методы ответа на этот вопрос.
Таким образом, упрощение сложного числового выражения позволяет определить, рационально ли заданное им число.
Теперь разберемся со знаком корня.
5 = 2 log 2 5 = 2 m n 5 n = 2 m
Очевидно, последнее равенство невозможно так как в левой и правой частях находятся соответственно нечетное и четное числа. Следовательно, сделанное предположение неверно, и число log 2 5 не является рациональным числом.
Действия с рациональными числами: правила, примеры, решения
Ниже рассмотрим правила основных математических действий над рациональными числами: сложение, вычитание, умножение и деление. Разберем теорию на практических примерах.
Действие сложения рациональных чисел
Рациональные числа содержат натуральные, тогда смысл действия сложения рациональных чисел сопоставим со смыслом сложения натуральных. Например, сумму рациональных чисел, записанную как 5 + 1 4 возможно описать следующим образом: к 5 целым предметам добавили четверть такого предмета, после чего полученное количество рассматривается совместно.
Сформулируем правила сложения рациональных чисел:
Сложение нуля с отличным от него рациональным числом
Прибавление нуля к любому числу дает то же число. Данное правило возможно записать в виде равенства: a + 0 = a (для любого рационального числа а). Используя переместительное свойство сложения, получим также верное равенство: 0 + a = a .
Сложение противоположных рациональных чисел
Сумма противоположных чисел равна нулю.
Сложение положительных рациональных чисел
В виде обыкновенной дроби возможно представить любое положительное рациональное число и использовать далее схему сложения обыкновенных дробей.
Решение
Осуществим сложение дробей с разными знаменателями:
6 10 + 5 9 = 54 90 + 50 90 = 104 90 = 1 7 45
Рациональные числа, которые подвергают действию сложения, возможно записать в виде конечных десятичных дробей или в виде смешанных чисел и, таким образом, осуществить сложение десятичных дробей и смешанных чисел соответственно.
Сложение рациональных чисел с разными знаками
Для того, чтобы осуществить сложение рациональных чисел с разными знаками, необходимо из бОльшего модуля слагаемых вычесть меньший и перед полученным результатом поставить знак того числа, модуль которого больше.
Решение
Сложение отрицательных рациональных чисел
Для того, чтобы произвести сложение отрицательных рациональных чисел, необходимо сложить модули заданных слагаемых, затем полученному результату присвоить знак минус.
Решение
Действие вычитания рациональных чисел
При вычитании из бОльшего положительного рационального числа мы либо производим вычитание обыкновенных дробей, либо, если это уместно, вычитание десятичных дробей или смешанных.
Решение
Необходимо из рационального числа 2 7 вычесть рациональное число 5 3 7
Решение
Действие умножения рациональных чисел
Общее понятие числа расширяется от натуральных чисел к целым, так же как от целых к рациональным. Все действия с целыми числами имеют те же свойства, что и действия с натуральными. В таком случае, и действия с рациональными числами также должны характеризоваться всеми свойствами действий с целыми числами. Но для действия умножения рациональных чисел присуще дополнительное свойство: свойство умножения взаимообратных чисел. Вышесказанному соответствуют все правила умножения рациональных чисел. Укажем их.
Умножение на нуль
Произведение любого рационального числа a на нуль есть нуль.
Умножение на единицу
Т.е. a · 1 = a или 1 · a = a (для любого рационального a ). Единица здесь является нейтральным числом по умножению.
Умножение взаимообратных чисел
К примеру, результатом произведения чисел 5 6 и 6 5 будет единица.
Умножение положительных рациональных чисел
В общих случаях умножение положительных рациональных чисел сводится к умножению обыкновенных дробей. Первым действием множители представляются в виде обыкновенных дробей, если заданные числа таковыми не являются.
Решение
Можно также работать и с конечными десятичными дробями. Удобнее будет в данном случае не переходить к действиям над обыкновенными дробями.
Решение
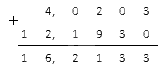
Перемножим десятичные дроби столбиком:
В частных случаях нахождение произведения рациональных чисел представляет собой умножение натуральных чисел, умножение натурального числа на обыкновенную или десятичную дробь.
Умножение рациональных чисел с разными знаками
Чтобы найти произведение рациональных чисел с разными знаками, необходимо перемножить модули множителей и полученному результату присвоить знак минус.
Решение
Умножение отрицательных рациональных чисел
Для того, чтобы найти произведение отрицательных рациональных чисел, необходимо перемножить модули множителей.
Перемножим их столбиком:
Полученный результат и будет являться искомым произведением.
Деление рациональных чисел
На множестве рациональных чисел деление не считается самостоятельным действием, поскольку оно производится через действие умножения. Собственно, этот смысл заложен в правило деления рациональных чисел.
Таким образом, деление рационального числа на другое рациональное число, отличное от нуля, сводится к действию умножения рациональных чисел.
Решение