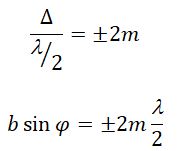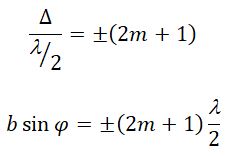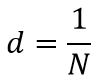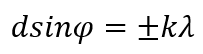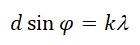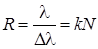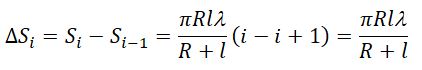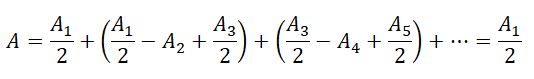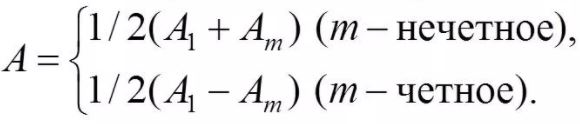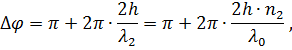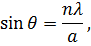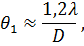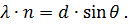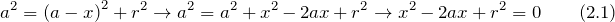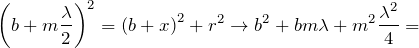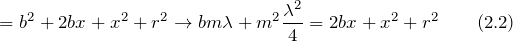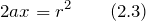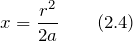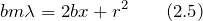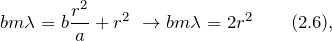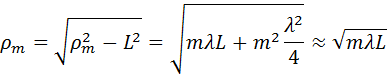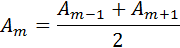при каком условии возможна дифракция волн

При каком условии возможна дифракция волн

Наблюдение дифракции осуществляется обычно по следующей схеме. На пути световой волны, распространяющейся от некоторого источника, помещается непрозрачная преграда, закрывающая часть волновой поверхности световой волны. За преградой располагается экран, на котором возникает дифракционная картина.

Свойства дифракции:

1) Дифракция волн – характерная особенность распространения волн независимо от их природы.

3) Дифракция волн зависит от соотношения между длиной волны и размером объекта, вызывающего дифракцию. В пределе при λ→0 законы волновой оптики переходят в законы геометрической оптики. Дифракция обнаруживается в тех случаях, когда размеры огибаемых препятствий соизмеримы с длиной волны.

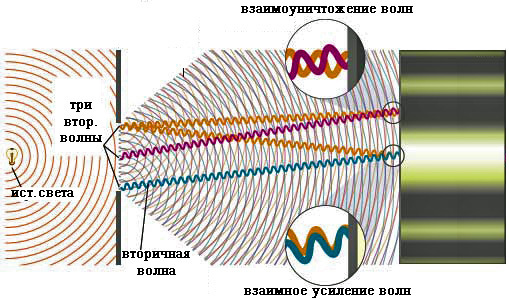
Каждый элемент волнового фронта можно рассматривать как центр вторичного возмущения, порождающего вторичные сферические волны, а результирующее световое поле в каждой точке пространства будет определяться интерференцией этих волн.

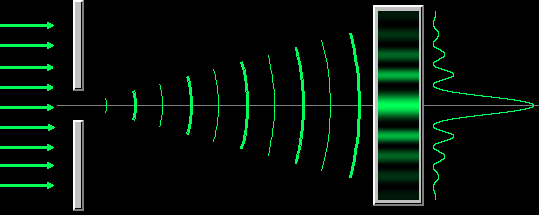
Дифракция Фраунгофера от одной щели

Дифракция Фраунгофера наблюдается, когда источник света сильно удален от места наблюдения, в результате фронт волны можно считать плоским.

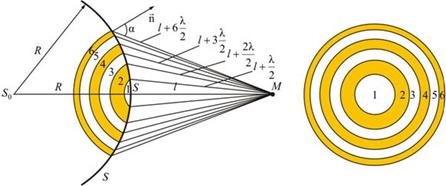
Разобьем MN на отрезки длиной λ/2. Параллельно произвольному направлению луча через точки разбиения (1, 2, 3) проведем линии, которые разделят открытую часть волновой поверхности MN на участки равной ширины – зоны Френеля, параллельные краям щели. По построению ∆ – разность хода лучей от краев зон Френеля равна λ/2. Это означает, что волны, идущие от двух соседних зон при наложении погасят друг друга. Т.о., если на открытой части волновой поверхности для данного направления наблюдения уложится целое четное число зон Френеля, то для данного направления будет наблюдаться min интенсивности, т.к. зоны попарно друг друга погасят.

Если число зон Френеля целое и нечетное, то в этом направлении будет наблюдаться max:

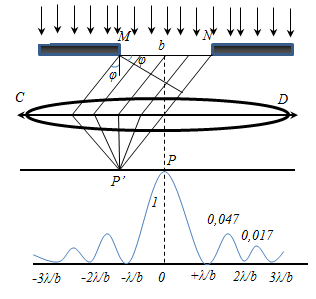
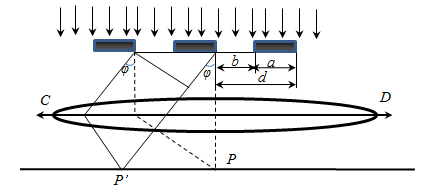
Дифракционная решетка

Совокупность большого числа щелей и промежутков между ними называется дифракционной решеткой.

В областях, в которых существует минимум при одной щели, минимумы будут и в случае N щелей, т. е. условие первичного минимума дифракционной решетки аналогично условию минимума для одной щели:

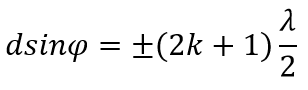
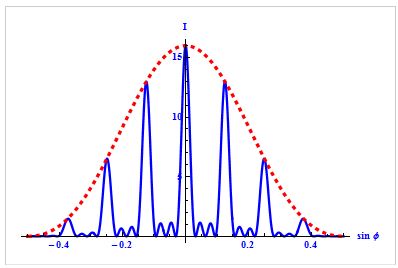
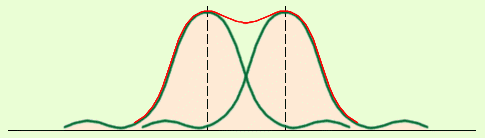
— условие главных минимумов.

Условие главных максимумов :

Эти максимумы расположены симметрично относительно центра (k = 0) и главного максимума.

Между главными максимумами будут расположены (N-1) дополнительных минимумов.

Разрешающая способность дифракционной решетки

Размер дифракционных изображений очень мал. Например, радиус центрального светлого пятна в фокальной плоскости линзы диаметром D = 5 см с фокусным расстоянием F = 50 см в монохроматическом свете с длиной волны λ = 500 нм приблизительно равен 0,006 мм. Но в высокоточных астро­но­ми­ческих приборах реализуется дифракци­он­ный предел качества изо­бра­же­ний. Вслед­ствие дифракционного размытия изобра­жения двух близких точек объекта могут оказаться неотличимыми от изо­бра­же­ния одной точки.

Спектральной разрешающей способностью R решетки, характеризующей возможность разделения с ее помощью двух близких спектральных линий с длинами волн λ и λ + Δλ, называется отношение длины волны λ к минимально возможному значению Δλ

Действие оптических приборов описывается законами геометрической оптики. Согласно этим законам можно различать с помощью микроскопа сколь угодно малые детали объекта; с помощью телескопа можно установить существование двух звезд при любых малых угловых расстояниях между ними. Однако в действительности это не так, и лишь волновая теория света позволяет разобраться в причинах предела разрешающей способности оптических приборов.

Метод зон Френеля

Колебания, возбуждаемые в точке M между двумя соседними зонами, противоположны по фазе, так как разность хода от этих зон до точки M Δ = λ/2.

Поэтому при сложении этих колебаний, они должны взаимно ослаблять друг друга: A = A₁ + A₂ + A₃ +. + A_i.

где A – амплитуда результирующего колебания, A_i – амплитуда колебаний, возбуждаемая i-й зоной Френеля.

Величина A_i зависит от площади S_i зоны и угла α_i между нормалью к поверхности и прямой, направленной в точку M.

Площадь одной зоны

Отсюда видно, что площадь зоны Френеля не зависит от номера зоны i. Это значит, что при не слишком больших i площади соседних зон одинаковы.

Отсюда следует, что углы между нормалью к зоне и направлением на точку M у соседних зон примерно равны, т.е. что амплитуды волн, приходящих в точку M от соседних зон, примерно равны.

.

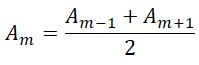
Тогда выражение для амплитуды можно записать в виде

Так как площади соседних зон одинаковы, то выражения в скобках равны нулю, значит результирующая амплитуда А = A₁ /2.

Интенсивность излучения J

Так как радиус центральной зоны мал ( r₁ = 0,16 мм), следовательно, можно считать, что свет от точки P до точки M распространяется прямолинейно.

Если на пути волны поставить непрозрачный экран с отверстием, оставляющим открытой только центральную зону Френеля, то амплитуда в точке M будет равна A₁. Соответственно, интенсивность в точке M будет в 4 раза больше, чем при отсутствии экрана (т.к. J = 4J₁ ). Интенсивность света увеличивается, если закрыть все четные зоны.

Таким образом, принцип Гюйгенса–Френеля позволяет объяснить прямолинейное распространение света в однородной среде.

Дифракция на простых объектах

Дифракция на щели

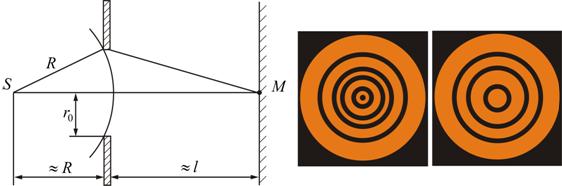
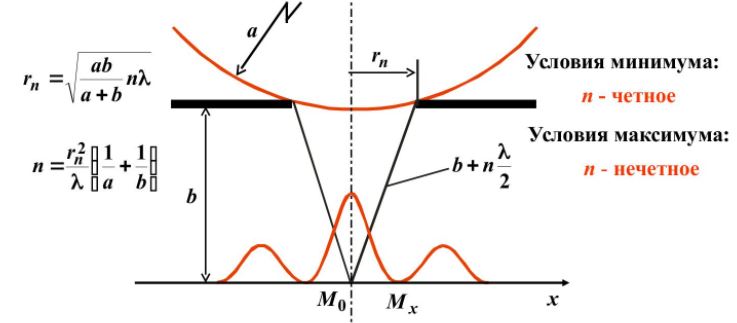
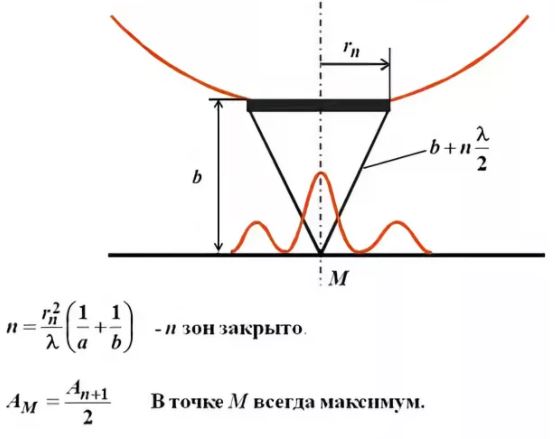
Разобьем открытую часть волновой поверхности на зоны Френеля. Вид дифракционной картины зависит от числа зон Френеля, открываемых отверстием. К огда отверстие открывает нечетное число зон Френеля, то амплитуда (интенсивность) в точке М будет больше, чем при свободном распространении волны; если четное, то амплитуда (интенсивность) будет равна нулю.

Дифракция на круглом отверстии при открытом чётном (слева) и не чётном (справа) числе зон.

Естественно, что если r₀>>λ, то никакой дифракционной картины не будет.

Дифракция от диска
Сферическая волна, распространяющаяся от точечного источника S, встречает на своем пути диск.

В центре тени светлое пятно

Амплитуда световых колебаний в точке M равна половине амплитуды, обусловленной первой открытой зоной. Если размер диска невелик (охватывает небольшое число зон), то действие первой зоны немногим отличается от действия центральной зоны волнового фронта. Таким образом, освещенность в точке M будет такой же, как и в отсутствие экрана. Вследствие симметрии центральная светлая точка будет окружена кольцами света и тени (вне границ геометрической тени).

Парадоксальное, на первый взгляд, заключение, в силу которого в самом центре геометрической тени может находиться светлая точка, было выдвинуто Пуассоном в 1818 г. и впоследствии было названо его именем. «Пятно Пуассона» подтверждает правильность теории Френеля.

Источник

Интерференция и дифракция

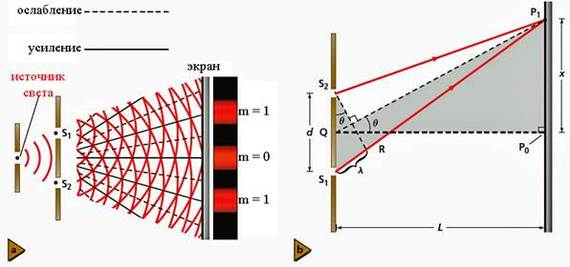
Интерференция – это сложение колебаний. В результате интерференции в каких-то точках пространства происходит рост амплитуды колебаний, а в других – их уменьшение. Неизменная картина интерференции наблюдается только тогда, когда разность складываемых колебаний постоянна (они когерентны). Очевидно, что когерентными могут быть колебания одинаковой частоты. Поэтому чаще всего изучают интерференцию монохроматических колебаний.

На фото изображена интерференция волн на поверхности воды.

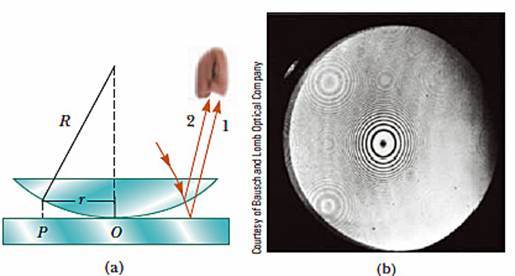
Интерференцию световых волн можно наблюдать, если положить стеклянную линзу на стеклянную пластинку (см. рисунок справа) и посмотреть на них сверху. Луч света (красные стрелки) падает сверху на линзу, преломляется, отражается от её нижней искривлённой поверхности и выходит из линзы (луч 2). Однако часть луча, упавшего на нижнюю поверхность линзы, выходит из неё, падает на стеклянную пластинку, отражается от неё, проходит через линзу и выходит из неё (луч 1). Лучи 1 и 2 когерентны, т.к. они возникли из одного луча.

Если попав в глаз, фаза этих лучей будет отличаться на целое число периодов, то эти лучи будут усиливать друг друга и мы увидим яркое пятно. В тех случаях, когда их разность фаз составит нечётное число полупериодов (Т/2, 3Т/2, 5Т/2 и т.д.) лучи уничтожат друг друга, и мы увидим тёмное пятно.

Очевидно, что разность фаз между лучами 1 и 2 зависит от толщины зазора между линзой и пластинкой. Поэтому, смотря сверху мы увидим чередующиеся тёмные и светлые кольца – кольца Ньютона (см. рисунок).

На фото ниже показаны интерференционные полосы для синего света (левая), для красного света (средняя) и для белого света (правая).

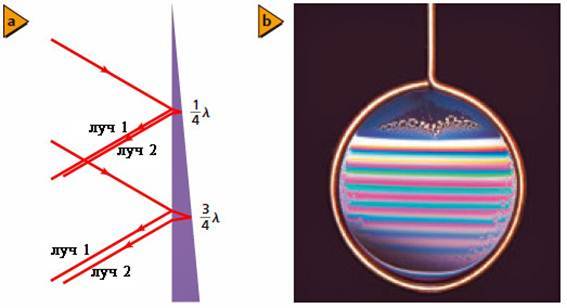
Интерференционные полосы можно наблюдать в свете, отражённом от вертикально расположенной мыльной плёнки (см. рисунок ниже). Толщина плёнки увеличивается сверху вниз, что изменяет разность хода между лучами, отражёнными от обеих поверхностей плёнки. На рисунке а схематически показан верхний красный луч, падающий слева на фиолетовую плёнку (в разрезе). Этот луч сразу отражается и получает обозначение (луч 1). Другая часть того же луча преломляется в плёнке, отражается от другой её поверхности (луч 2) и продолжает двигаться рядом с лучом 1. Если при этом разница фаз между лучами 1 и 2 станет кратной периоду колебаний, то лучи будут усиливать друг друга, и мы увидим яркую полосу. Если же эта разница фаз составит нечётное число полупериодов (Т/2, 3Т/2, 5Т/2 и т.д.), то они уничтожат друг друга, а мы увидим тёмную полосу.

Следует отметить, что волны при отражении изменяют фазу на 180° (или p), если отражаются от более оптически плотной среды, например, при отражении света в воздухе от воды. Если отражение происходит от менее оптически плотной среды, то изменение фазы волны не происходит.

где l0 – длина волны света в вакууме.

Дифракцией называют явления, связанные со свойством волн огибать препятствия, т.е отклоняться от прямолинейного распространения.

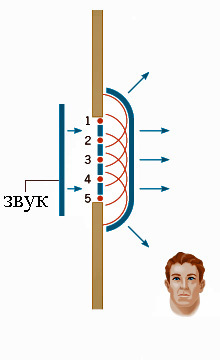
На рисунке ниже показано, как меняют направление звуковые волны после прохождения через отверстие в стене. Согласно принципа Гюйгенса области 1-5 становятся вторичными источниками сферических звуковых волн. Видно, что вторичные источники в областях 1 и 5 приводят к огибанию волнами препятствий.

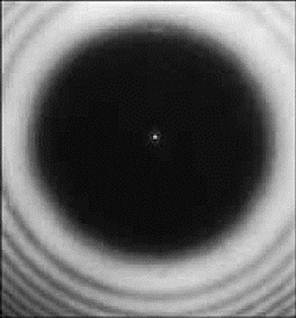
Ниже показано фото тени от монеты на экране при освещении её источником монохроматического света. Видно, что в центре тени есть яркое пятно, образованное интерференцией лучей, огибающих край монеты. Интерференция этих лучей приводит к появлению чередующихся тёмных и ярких колец, окружающих тёмный диск тени. Этот эксперимент тоже является иллюстрацией явления дифракции света.

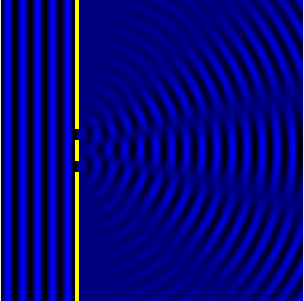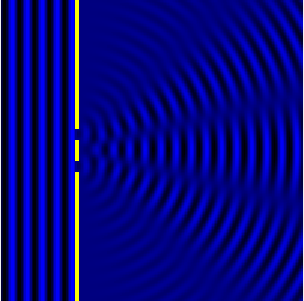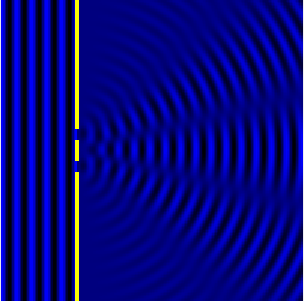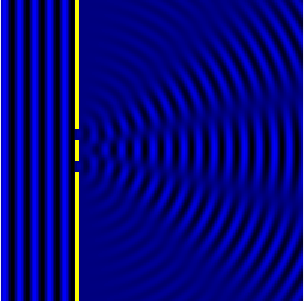
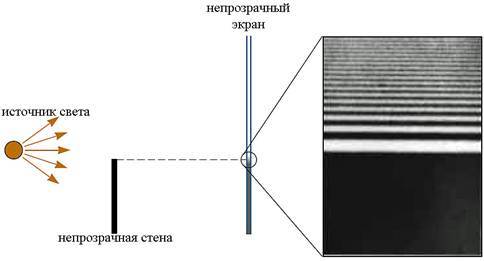
Ниже показано увеличенное фото тени верхнего края непрозрачной стены на экране. Видно, что переход из тёмной части тени в освещённую происходит не резко, а через последовательность чередующихся тёмных и ярких полос. Эти полосы являются результатом дифракции лучей света на краю препятствия и последующей их интерференции.

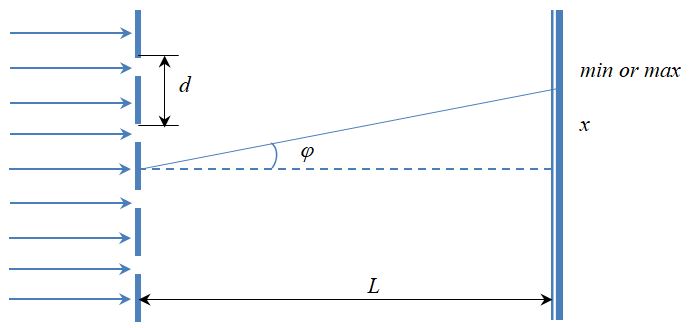
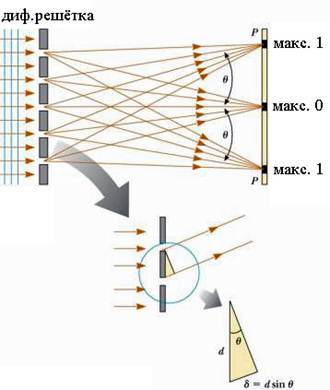
Если расстояние L до экрана, на котором наблюдают дифракционную картину, гораздо больше ширины a щели (см. рисунок ниже), то угол, под которым виден первый дифракционный минимум номер n (см. yn на рисунке), можно вычислить из соотношения

Дифракция света наблюдается, если он проходит через круглое отверстие (см. левый рисунок). При этом дифракционная картина состоит из центрального яркого пятна, окружённого чередой тёмных и ярких колец. При этом угловой диаметр q1 центрального яркого пятна равен

Таким образом, чем больше будет диаметр входной линзы или зеркала телескопа, тем больше звёзд мы увидим на небе.

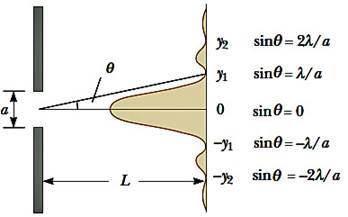
Дифракционная решётка – это прозрачная пластинка, на которую через одинаковое расстояние d (период решётки) нанесены параллельные штрихи. Плоский фронт световой волны падает слева на дифракционную решётку (см. рисунок) и претерпевает дифракцию на её штрихах. После интерференции прошедших через решётку лучей появляются направления, вдоль которых наблюдаются дифракционные максимумы и минимумы интенсивности света.

Угол qn, под которым виден первый дифракционный максимум номер n, легко вычислить, если считать, что расстояние до экрана Р гораздо больше периода решётки d:

На рисунке справа показано, как дифракционная решётка расщепляет голубой луч лазера.

Дифракционная решётка не только может отклонять лучи, как призма, но и разлагать их в спектр. Справа показано, что происходит с белым светом, после того, как он проходит через дифракционную решётку. Видно, что дифракционная картина в этом случае представляет собой наложение дифракционных картин для цветов, образующих белый свет

Явления дифракции и интерференции света помогают Природе раскрашивать всё живое, не прибегая к использованию красителей

Источник

Дифракция волн

Определение и основные сведения о дифракции волн

Волны могут огибать края препятствий. Если размер препятствия сравним с длиной волны, то огибая препятствие, волна смыкается за препятствием. Например, если из воды в пруду торчит ветка. Создадим волну, бросив камень в воду. Эта волна обогнет торчащую из воды ветку, и будет распространяться за ней так, как – будто ветки не было. Однако если размеры препятствия будут больше по сравнению с длиной волны, то огибание не произойдет и за препятствием образуется «тень», волна за него не приникнет. Любой вид волн может огибать препятствия (световые волны, звуковые, механические и т.д.).

При дифракции происходит искривление поверхности волны у краев препятствия. Особенно явно дифракция проявляется в том случае, если размеры препятствия сравнимы с длинами волн.

Явление дифракции можно объяснить при помощи принципа Гюйгенса, так как любую точку поля волны следует рассматривать как источник вторичных волн, которые распространяются по всем направлениям, в том числе и в область геометрической тени препятствия. Исторически явление дифракции начали изучать в оптике, изучая свойства света.

Дифракция света. Основные положения теории Френеля

Дифракция света – это пакет явлений, связанных с волновой природой света, которые можно наблюдать при его распространении в веществе с выраженными неоднородностями. Явления, которые подтверждают явление дифракции световой волны: отклонение света от прямолинейного распространения при прохождении сквозь отверстия в непрозрачных экранах, огибание границ непрозрачных тел.

Рассматривая дифракцию света Френель выдвинул ряд положений, которые принимаются без доказательства и составивших принцип Гюйгенса – Френеля:

Френель предложил свой метод разбиения поверхности волны на зоны, которые помогают упрощать решения задач.

При решении задач выделяют: дифракцию в сходящихся лучах (дифракция Френеля) и дифракцию в параллельных лучах (дифракция Фрауггофера).

Примеры решения задач

Явление дифракции накладывает ограничения на возможности телескопа. Из-за дифракции у края оправы объектива прибора будет наблюдаться не точка, как изображение, например, звезды, а совокупность светлых и темных колец. В том случае, если две звезды расположены близко друг к другу (угловое расстояние между ними мало), то кольца налагаются друг на друга, и нет возможности различить какое число звезд действительно имеется.

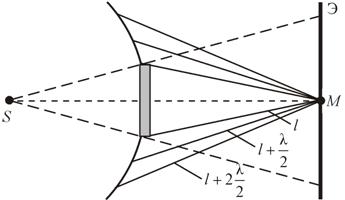
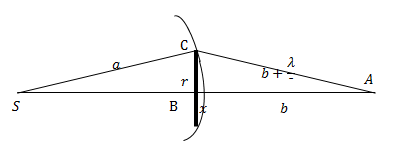
Задание	Посередине между точечным источником света и экраном расположен непрозрачный диск радиусом r. Длина волны света равна 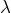. Каково расстояние от источника до экрана, на котором наблюдается картина дифракции, если диск закрывает только центральную зону Френеля?
Решение	Сделаем рисунок.

Рассматривая прямоугольный треугольник SBC (рис.1) запишем:

Для прямоугольного треугольника ABC имеем:

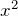
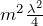
Величины и – малы и ими можно пренебречь. Следовательно, выражение (2.1) можно упростить до вида:

И из формулы (2.3) найти x:

Выражение (2.2) упрощаем до:

Подставим в (2.5) найденный x, получим:

где мы использовали условие задачи: .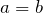

Выразим b и используем то, что 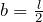, для нахождения искомого расстояния (l):

Источник

Дифракция света

Дифракцией света называется явление отклонения света от прямолинейного направления распространения при прохождении вблизи препятствий. Как показывает опыт, свет при определенных условиях может заходить в область геометрической тени. Если на пути параллельного светового пучка расположено круглое препятствие (круглый диск, шарик или круглое отверстие в непрозрачном экране), то на экране, расположенном на достаточно большом расстоянии от препятствия, появляется дифракционная картина – система чередующихся светлых и темных колец. Если препятствие имеет линейный характер (щель, нить, край экрана), то на экране возникает система параллельных дифракционных полос.

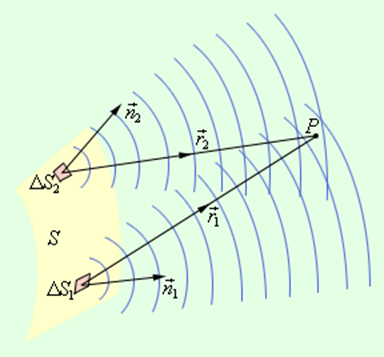
Дифракционные явления были хорошо известны еще во времена Ньютона, но объяснить их на основе корпускулярной теории света оказалось невозможным. Первое качественное объяснение явления дифракции на основе волновых представлений было дано английским ученым Т.Юнгом. Независимо от него в 1818 г. французский ученый О.Френель развил количественную теорию дифракционных явлений. В основу теории Френель положил принцип Гюйгенса, дополнив его идеей об интерференции вторичных волн. Принцип Гюйгенса в его первоначальном виде позволял находить только положения волновых фронтов в последующие моменты времени, т. е. определять направление распространения волны. По существу, это был принцип геометрической оптики. Гипотезу Гюйгенса об огибающих вторичных волнах Френель заменил физически ясным положением, согласно которому вторичные волны, приходя в точку наблюдения, интерферируют друг с другом. Принцип Гюйгенса–Френеля также представлял собой определенную гипотезу, но последующий опыт подтвердил ее справедливость. В ряде практически важных случаев решение дифракционных задач на основе этого принципа дает достаточно хороший результат. Рис. 3.8.1 иллюстрирует принцип Гюйгенса–Френеля.

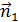
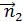
Принцип Гюйгенса–Френеля. ΔS₁ и ΔS₂ – элементы волнового фронта, и – нормали

Пусть поверхность S представляет собой положение волнового фронта в некоторый момент. В теории волн под волновым фронтом понимают поверхность, во всех точках которой колебания происходят с одним и тем же значением фазы (синфазно). В частности, волновые фронта плоской волны – это семейство параллельных плоскостей, перпендикулярных направлению распространения волны. Волновые фронта сферической волны, испускаемой точечным источником – это семейство концентрических сфер.

Для того чтобы определить колебания в некоторой точке P, вызванное волной, по Френелю нужно сначала определить колебания, вызываемые в этой точке отдельными вторичными волнами, приходящими в нее от всех элементов поверхности S (ΔS₁, ΔS₂ и т. д.), и затем сложить эти колебания с учетом их амплитуд и фаз. При этом следует учитывать только те элементы волновой поверхности S, которые не загораживаются каким-либо препятствием.

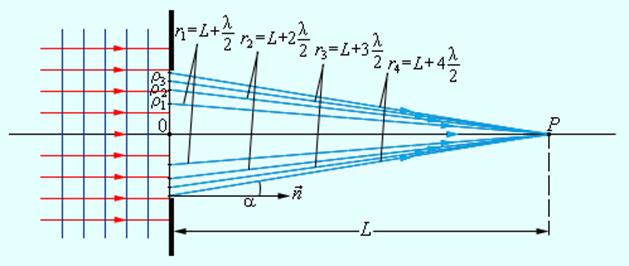
Рассмотрим в качестве примера простую дифракционную задачу о прохождении плоской монохроматической волны от удаленного источника через небольшое круглое отверстие радиуса R в непрозрачном экране (рис. 3.8.2).

Дифракция плоской волны на экране с круглым отверстием

Точка наблюдения P находится на оси симметрии на расстоянии L от экрана. В соответствии с принципом Гюйгенса–Френеля следует мысленно заселить волновую поверхность, совпадающую с плоскостью отверстия, вторичными источниками, волны от которых достигают точки P. В результате интерференции вторичных волн в точке P возникает некоторое результирующее колебание, квадрат амплитуды которого (интенсивность) нужно определить при заданных значениях длины волны λ, амплитуды A₀ падающей волны и геометрии задачи. Для облегчения расчета Френель предложил разбить волновую поверхность падающей волны в месте расположения препятствия на кольцевые зоны (зоны Френеля) по следующему правилу: расстояние от границ соседних зон до точки P должны отличается на половину длины волны, т. е.

…

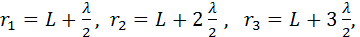
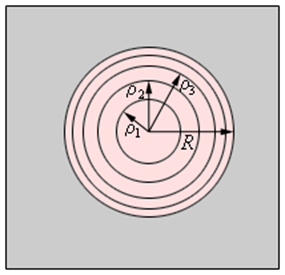
Если смотреть на волновую поверхность из точки P, то границы зон Френеля будут представлять собой концентрические окружности (рис. 3.8.3).

Границы зон Френеля в плоскости отверстия

Из рис. 3.8.2 легко найти радиусы ρm зон Френеля:

где Am – амплитуда колебаний, вызванных m-й зоной.

С хорошим приближением можно считать, что амплитуда колебаний, вызываемых некоторой зоной, равна среднему арифметическому из амплитуд колебаний, вызываемых двумя соседними зонами, т. е.

Так как расстояния от двух соседних зон до точки наблюдения отличаются на λ / 2, следовательно, возбуждаемые этими зонами колебания находится в противофазе. Поэтому волны от любых двух соседних зон почти гасят друг друга. Суммарная амплитуда в точке наблюдения есть

Источник