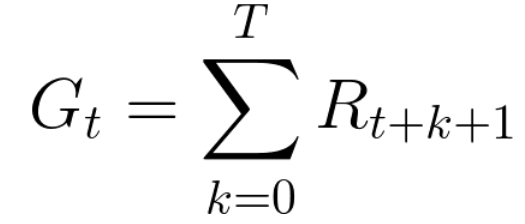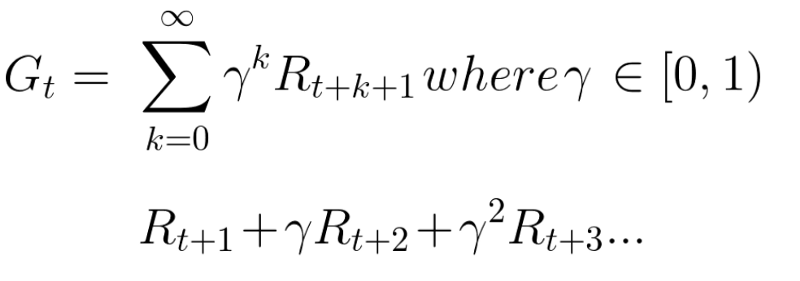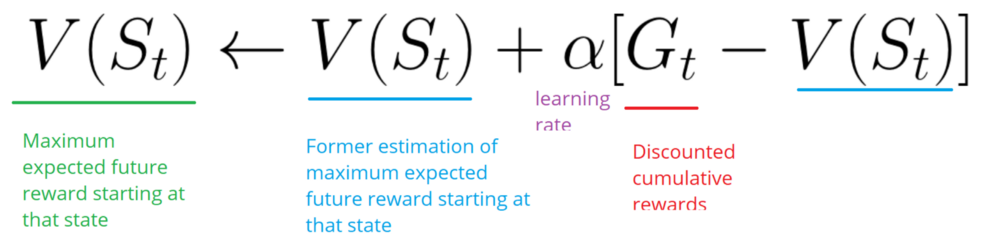reinforcement learning это область машинного обучения
Обучение с подкреплением
| Определение: |
| Обучение с подкреплением (англ. reinforcement learning) — способ машинного обучения, при котором система обучается, взаимодействуя с некоторой средой. |
Содержание
Обучение с подкреплением [ править ]
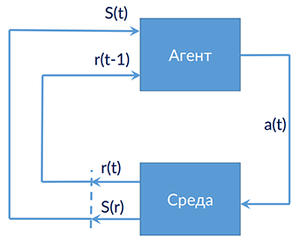
В обучении с подкреплением существует агент (agent) взаимодействует с окружающей средой (environment), предпринимая действия (actions). Окружающая среда дает награду (reward) за эти действия, а агент продолжает их предпринимать.
Алгоритмы с частичным обучением пытаются найти стратегию, приписывающую состояниям (states) окружающей среды действия, одно из которых может выбрать агент в этих состояниях.
Среда обычно формулируется как марковский процесс принятия решений (МППР) с конечным множеством состояний, и в этом смысле алгоритмы обучения с подкреплением тесно связаны с динамическим программированием. Вероятности выигрышей и перехода состояний в МППР обычно являются величинами случайными, но стационарными в рамках задачи.
При обучении с подкреплением, в отличии от обучения с учителем, не предоставляются верные пары «входные данные-ответ», а принятие субоптимальнх решений (дающих локальный экстремум) не ограничивается явно. Обучение с подкреплением пытается найти компромисс между исследованием неизученных областей и применением имеющихся знаний (exploration vs exploitation). Баланс изучения-применения при обучении с подкреплением исследуется в задаче о многоруком бандите.
Формально простейшая модель обучения с подкреплением состоит из:
для МППР без терминальных состояний (где [math]0 \leq \gamma \leq 1[/math] — дисконтирующий множитель для «предстоящего выигрыша»).
Таким образом, обучение с подкреплением особенно хорошо подходит для решения задач, связанных с выбором между долгосрочной и краткосрочной выгодой.
Постановка задачи обучения с подкреплением [ править ]
[math]S[/math] — множество состояний среды
Игра агента со средой:
Алгоритмы [ править ]
Теперь, когда была определена функция выигрыша, нужно определить алгоритм, который будет использоваться для нахождения стратегии, обеспечивающей наилучший результат.
Наивный подход к решению этой задачи подразумевает следующие шаги:
Первая проблема такого подхода заключается в том, что количество доступных стратегий может быть очень велико или бесконечно. Вторая проблема возникает, если выигрыши стохастические — чтобы точно оценить выигрыш от каждой стратегии потребуется многократно применить каждую из них. Этих проблем можно избежать, если допустить некоторую структуризацию и, возможно, позволить результатам, полученным от пробы одной стратегии, влиять на оценку для другой. Двумя основными подходами для реализации этих идей являются оценка функций полезности и прямая оптимизация стратегий.
Поэтому построение искомой оценки при [math]\gamma \in (0, 1)[/math] неочевидно. Однако, можно заметить, что [math]R[/math] образуют рекурсивное уравнение Беллмана:
Подставляя имеющиеся оценки [math]V[/math] и применяя метод градиентного спуска с квадратичной функцией ошибок, мы приходим к алгоритму обучения с временными воздействиями (temporal difference (TD) learning). В простейшем случае и состояния, и действия дискретны и можно придерживаться табличных оценок для каждого состояния.
Другие похожие методы: Адаптивный эвристический критик (Adaptive Heuristic Critic, AHC), SARSA и Q-обучение (Q-learning).
Задача о многоруком бандите (The multi-armed bandit problem) [ править ]
Формулировка [ править ]
[math]A[/math] — множество возможных действий (ручек автомата),
Игра агента со средой:
Выбор действия [math]a_t[/math] на шаге [math]t[/math] влечет награду [math]R(a_t)[/math] при этом [math]R(a)[/math] [math]\forall a \in A[/math] есть случайная величина, распределение которой неизвестно.
Состояние среды у нас от шага к шагу не меняется, а значит множество состояний [math]S[/math] тривиально, ни на что не влияет, поэтому его можно проигнорировать.
Для простоты будем полагать, что каждому действию соответствует некоторое распределение, которое не меняется со временем. Если бы мы знали эти распределения, то очевидная стратегия заключалась бы в том, чтобы подсчитать математическое ожидание для каждого из распределений, выбрать действие с максимальным математическим ожиданием и теперь совершать это действие на каждом шаге.
Задача является модельной для понимания конфликта между exploitation—exploration.
Жадная (greedy) стратегия [ править ]
На каждом шаге [math]t[/math]
В данном случае достаточно попробовать в начале каждую из ручек вместо того, чтобы фокусироваться только на одной. Но если награда случайная величина, то единичной попытки будет не достаточно. Поэтому модифицируем жадную стратегию следующим образом:
На каждом шаге [math]t[/math]
Стратегия Softmax [ править ]
[math]\tau \in (0, \infty)[/math] — параметр, с помощью которого можно настраивать поведение алгоритма.
При [math]\tau \rightarrow \infty[/math] стратегия стремится к равномерной, то есть softmax будет меньше зависеть от значения выигрыша и выбирать действия более равномерно (exploration).
При [math]\tau \rightarrow 0[/math] стратегия стремится к жадной, то есть алгоритм будет больше ориентироваться на известный средний выигрыш действий (exploitation).
Экспонента используется для того, чтобы данный вес был ненулевым даже у действий, награда от которых пока нулевая.
Эвристика: параметр [math]\tau[/math] имеет смысл уменьшать со временем.
Метод UCB (upper confidence bound) [ править ]
Предыдущие алгоритмы при принятии решения используют данные о среднем выигрыше. Проблема в том, что если действие даёт награду с какой-то вероятностью, то данные от наблюдений получаются шумные и мы можем неправильно определять самое выгодное действие.
Алгоритм верхнего доверительного интервала (upper confidence bound или UCB) — семейство алгоритмов, которые пытаются решить эту проблему, используя при выборе данные не только о среднем выигрыше, но и о том, насколько можно доверять значениям выигрыша.
Также как softmax в UCB при выборе действия используется весовой коэффициент, который представляет собой верхнюю границу доверительного интервала (upper confidence bound) значения выигрыша:
[math]b_a = \sqrt<\frac<2 \ln<\sum_a P_a>>
В отличие от предыдущих алгоритмов UCB не использует в своей работе ни случайные числа для выбора действия, ни параметры, которыми можно влиять на его работу. В начале работы алгоритма каждое из действий выбирается по одному разу (для того чтобы можно было вычислить размер бонуса для всех действий). После этого в каждый момент времени выбирается действие с максимальным значением весового коэффициента.
Несмотря на это отсутствие случайности результаты работы этого алгоритма выглядят довольно шумно по сравнению с остальными. Это происходит из-за того, что данный алгоритм сравнительно часто выбирает недоисследованные действия.
Q-learning [ править ]
Таким образом, алгоритм это функция качества от состояния и действия:
Введение в обучение с подкреплением для начинающих
Обучение с подкреплением в – это способ машинного обучения, при котором система обучается, взаимодействуя с некоторой средой.
В последние годы мы наблюдаем прогресс в исследованиях в данной области. Например DeepMind, Deep Q learning в 2014, победа чемпиона мира в Go с помощью алгоритма AlphaGo в 2016, OpenAl и PPO в 2017
В этой статье мы сфокусируемся на изучении различных архитектур, которые активно используются вместе с обучением с подкреплением в наши дни для решения различного рода проблем, а именно Q-learning, Deep Q-learning, Policy Gradients, Actor Critic и PPO.
Из этой статьи, вы узнаете:
Очень важно освоить все эти элементы, прежде чем погружаться в реализацию системы глубинного обучения с подкреплением.
Идея обучения с подкреплением заключается в том, что система будет учиться в среде, взаимодействовать с ней и получать вознаграждение за выполнение действий.
Представьте, что вы ребенок в гостиной. Вы увидели камин и захотели подойти к нему.
Тут тепло, вы хорошо себя чувствуете. Вы понимаете, что огонь – это хорошо.
Но потом вы пытаетесь дотронуться до огня и обжигаете руку. Только что вы осознали, что огонь – это хорошо, но только тогда, когда находитесь на достаточном расстоянии, потому что он производит тепло. Если подойти слишком близко к нему, вы обожжетесь.
Вот как люди учатся через взаимодействие. Обучение с подкреплением – это просто вычислительный подход к обучению на основе действий.
Как выглядит обучение с подкреплением

Давайте в качестве примера представим, что система учится играть в Super Mario Bros. Процесс обучения с подкреплением может быть смоделирован как цикл, который работает следующим образом:
Этот цикл ОП выводит последовательность состояний, действий и вознаграждений.
Цель системы – максимизировать ожидаемое вознаграждение.
Главная идея гипотезы вознаграждения
Почему целью системы является максимизация ожидаемого вознаграждения?
Обучение с подкреплением основано на идее гипотезы вознаграждения. Все цели можно описать максимизацией ожидаемого вознаграждения.
Вознаграждение на каждом временном шаге (t) может быть записано как:
Что эквивалентно:
Однако на самом деле мы не можем просто добавить такие награды. Награды, которые приходят раньше (в начале игры), более вероятны, так как они более предсказуемы, чем будущие вознаграждения.
Допустим, ваш герой – это маленькая мышь, а противник – кошка. Цель игры состоит в том, чтобы съесть максимальное количество сыра, прежде чем быть съеденным кошкой.
Как мы можем видеть на изображении, скорее всего мышь будет есть сыр рядом с собой, нежели сыр, расположенный ближе к кошке (т.к. чем ближе мы к кошке, тем она опаснее).
Как следствие, ценность награды рядом с кошкой, даже если она больше обычного (больше сыра), будет снижена. Мы не уверены, что сможем его съесть.
Перерасчет награды, мы делаем таким способом:
Мы определяем ставку дисконтирования gamma. Она должна быть в пределах от 0 до 1.
Ожидаемые вознаграждения можно рассчитать по формуле:
Другими словами, каждая награда будет уценена с помощью gamma к показателю времени (t). По мере того, как шаг времени увеличивается, кошка становится ближе к нам, поэтому будущее вознаграждение все менее и менее вероятно.
Эпизодические или непрерывные задачи
У нас может быть два типа задач: эпизодические и непрерывные.
Эпизодические задачи
В этом случае у нас есть начальная и конечная точка. Это создает эпизод: список состояний, действий, наград и будущих состояний.
Например в Super Mario Bros, эпизод начинается с запуска нового Марио и заканчивается, когда вы убиты или достигли конца уровня.
Непрерывные задачи
Это задачи, которые продолжаются вечно. В этом случае система должна научиться выбирать оптимальные действия и одновременно взаимодействовать со средой.
Как пример можно привести систему, которая автоматически торгует акциями. Для этой задачи нет начальной точки и состояния терминала. Что касается нашей задачи, то герой будет бежать, пока мы не решим остановить его.
Борьба методов: Монте-Карло против Временной разницы
Существует два основных метода обучения:
Монте-Карло
Когда эпизод заканчивается, система смотрит на накопленное вознаграждение, чтобы понять насколько хорошо он выполнил свою задачу. В методе Монте-Карло награды получают только в конце игры.
Затем, мы начинаем новую игру с новыми знаниями. С каждым разом система проходит этот уровень все лучше и лучше.
Возьмем эту картинку как пример:
Временная разница: обучение на каждом временном шаге
Этот метод не будет ждать конца эпизода, чтобы обновить максимально возможное вознаграждение. Он будет обновлять V в зависимости от полученного опыта.
Метод вызывает TD (0) или One step TD (обновление функции value после любого отдельного шага).
Он будет только ждать следующего временного шага, чтобы обновить значения. В момент времени t+1 обновляются все значения, а именно вознаграждение меняется на Rt+1, а текущую оценка на V(St+1).
Разведка или эксплуатация?
Прежде чем рассматривать различные стратегии решения проблем обучения с подкреплением, мы должны охватить еще одну очень важную тему: компромисс между разведкой и эксплуатацией.
Помните, что цель нашей системы заключается в максимизации ожидаемого совокупного вознаграждения. Однако мы можем попасть в ловушку.
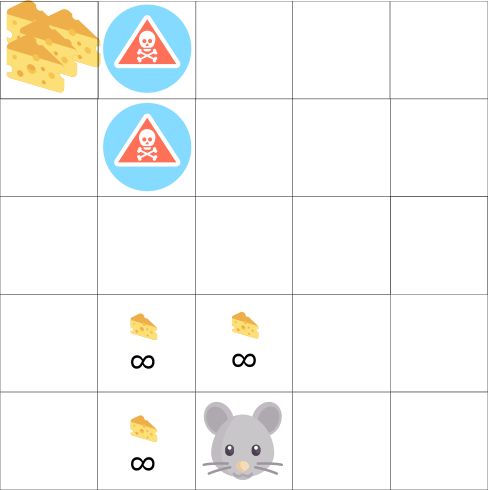
В этой игре, наша мышь может иметь бесконечное количество маленьких кусков сыра (+1). Однако на вершине лабиринта есть гигантский кусок сыра (+1000).
Но, если мы сосредоточимся только на вознаграждении, наша система никогда не достигнет того самого большого куска сыра. Вместо этого она будет использовать только ближайший источник вознаграждений, даже если этот источник мал (эксплуатация).
Но если наша система проведет небольшое исследование, она найдет большую награду.
Это то, что мы называем компромиссом между разведкой и эксплуатацией. Мы должны определить правило, которое поможет справиться с этим компромиссом.
Три подхода к обучению с подкреплением
Теперь, когда мы определили основные элементы обучения с подкреплением, давайте перейдем к трем подходам для решения проблем, связанных с этим обучением.
На основе значений
В обучении с подкреплением на основе значений целью является оптимизация функции V(s).
Функция value – это функция, которая сообщает нам максимальное ожидаемое вознаграждение, которое получит система.
Значение каждой позиции – это общая сумма вознаграждения, которую система может накопить в будущем, начиная с этой позиции.
Система будет использовать эту функцию значений для выбора состояния на каждом шаге. Она принимает состояние с наибольшим значением.
На основе политики
В обучении с подкреплением на основе политики мы хотим напрямую оптимизировать функцию политики π (s) без использования функции значения.
Политика – это то, что определяет поведение системы в данный момент времени.
Это позволяет нам сопоставить каждую позицию с наилучшим действием.
Существует два типа политики:
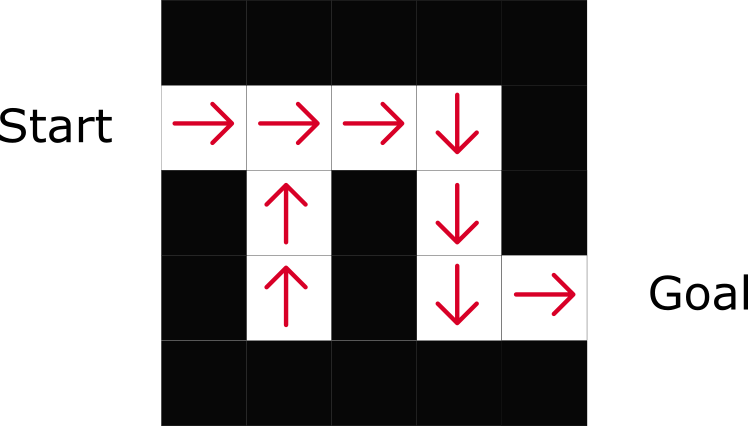
Как можно заметить, политика прямо указывает на лучшие действия для каждого шага.
На основе модели
В подходе на основании модели мы моделируем среду. Это означает, что мы создаем модель поведения среды.
Проблема каждой среды заключается в том, что понадобятся различные представления данной модели. Вот почему мы особо не будем раскрывать эту тему.
В этой статье было довольно много информации. Убедитесь, что действительно поняли весь материал, прежде чем продолжить изучение. Важно освоить эти элементы перед тем как начать самую интересную часть: создание ИИ, который играет в видеоигры.
Что не так с обучением с подкреплением (Reinforcement Learning)?
Еще в начале 2018 года вышла статья Deep Reinforcement Learning Doesn’t Work Yet («Обучение с подкреплением пока не работает»). Основная претензия которой сводилась к тому, что современные алгоритмы обучения с подкреплением требуют для решения задачи примерно столько же времени, как и обычный случайный поиск.
Изменилось ли что-то с того времени? Нет.
Обучение с подкреплением считается одним из трех основных путей к созданию сильного ИИ. Но трудности, с которыми сталкивается эта область машинного обучения, и методы, которыми ученые пытаются бороться с этими трудностями, наводят на мысль что, возможно, с самим этим подходом имеются фундаментальные проблемы.
Постойте, что значит один из трех? А остальные два какие?
С учетом успеха нейронных сетей в последние годы и анализом того, как они работают с высокоуровневыми когнитивными способностями, считавшимися ранее характерными только для человека и высших животных, на сегодняшний день в научном сообществе сложилось мнение, что можно выделить три основных подхода к созданию сильного ИИ на основе нейронных сетей, которые можно считать более менее реалистичными:
1. Обработка текстов
В мире накоплено огромное количество книг и текста в интернете, в том числе учебников и справочников. Текст удобен и быстр для обработки на компьютере. Теоретически, этого массива текстов должно хватить для обучения сильного разговорного ИИ.
При этом подразумевается, что в этих текстовых массивах отражено полное устройство мира (как минимум, оно описано в учебниках и справочниках). Но это совершенно не факт. Тексты как вид представления информации сильно оторваны от реального трехмерного мира и течения времени, в котором мы живем.
Хорошими примерами ИИ, обученными на текстовых массивах, являются чат-боты и автоматические переводчики. Так как для перевода текста нужно понять смысл фразы и пересказать его новыми словами (на другом языке). Существует распространенное заблуждение, что правила грамматики и синтаксиса, включая описание всех возможных исключений, полностью описывают конкретный язык. Это не так. Язык — это лишь вспомогательный инструмент в жизни, он легко меняется и адаптируется под новые ситуации.
Проблема обработки текста (хоть экспертными системами, хоть нейронными сетями) в том, что не существует набора правил, какие фразы в каких ситуациях нужно применять. Обратите внимание — не правил построения самих фраз (чем занимается грамматика и синтаксис), а именно какие фразы в каких жизненных ситуациях. В одной и той же ситуации люди произносят на разных языках фразы, которые вообще никак друг с другом не связаны с точки зрения структуры языка. Сравните фразы при крайней степени удивления: «о, боже!» и «o, holy shit!». Ну и как между ними провести соответствие, зная языковую модель? Да никак. Так случайно сложилось исторически. Нужно знать ситуацию и что в ней обычно говорят на конкретном языке. Именно из-за этого автоматические переводчики пока такие несовершенные.
Можно ли выделить эти знания чисто из массива текстов — неизвестно. Но если автоматические переводчики станут идеально переводить, не делая глупых и нелепых ошибок, то это будет доказательством, что создание сильного ИИ только на основе текста возможно.
2. Распознавание изображений
Посмотрите на это изображение
Глядя на эту фотографию мы понимаем, что съемка велась ночью. Судя по флагам, ветер дует справа налево. А судя по правостороннему движению, дело не происходит в Англии или Австралии. Никакая эта информация не указана явно в пикселях картинки, это внешние знания. На фото есть лишь признаки, по которым мы можем воспользоваться знаниями, полученными из других источников.
О том и речь… И найдите себе девушку, наконец
Поэтому считается, что если обучить нейронную сеть распознавать объекты на картинке, то у нее сложится внутреннее представление о том, как устроен реальный мир. И это представление, полученное по фотографиям, уж точно будет соответствовать нашему реальному и настоящему миру. В отличие от массивов текстов, где это не гарантировано.
Ценность нейронных сетей, обученных на массиве фотографий ImageNet (а теперь и OpenImages V4, COCO, KITTI, BDD100K и другие) вовсе не в факте распознавания котика на фото. А в том, что хранится в предпоследнем слое. Именно там находится набор высокоуровневых features, описывающих наш мир. Вектора в 1024 числа достаточно, чтобы из него получить описание 1000 разных категорий объектов с 80% точностью (и в 95% случаев правильный ответ будет в 5 ближайших вариантах). Только вдумайтесь в это.
Именно поэтому эти features из предпоследнего слоя так успешно используются в совершенно различных задачах по компьютерному зрению. Через Transfer Learning и Fine Tuning. Из этого вектора в 1024 числа можно получить, например, карту глубины по картинке
(пример из работы, где используется практически не измененная предобученная сеть Densenet-169)
Или определять позу человека. Применений много.
Как следствие, распознавание изображений потенциально можно использовать для создания сильного ИИ, так как оно действительно отражает модель нашего реального мира. От фотографии к видео один шаг, а видео — это и есть наша жизнь, так как около 99% информации мы получаем зрительно.
Но по фотографии совершенно непонятно, как мотивировать нейронную сеть думать и делать выводы. Ее можно обучить отвечать на вопросы вроде «сколько карандашей лежит на столе?» (этот класс задач называется Visual Question Answering, пример такого датасета: https://visualqa.org). Или давать текстовое описание тому, что происходит на фото. Это класс задач Image Captioning.
Но является ли это интеллектом? Развив этот подход, в недалеком будущем нейронные сети смогут отвечать по видео на вопросы вроде «На проводах сидело два воробья, один из них улетел, сколько осталось воробьев?». Это уже настоящая математика, в чуть более усложненных случаях недоступная животным и находящаяся на уровне человеческого школьного образования. Особенно, если кроме воробьев, там рядом будут сидеть синички, но их не нужно учитывать, так как вопрос был только про воробьев. Да, это определенно будет интеллект.
3. Обучение с подкреплением (Reinforcement Learning)
Идея очень проста: поощрять действия, ведущие к награде, и избегать ведущих к неудаче. Это универсальный способ обучения и, очевидно, он со всей определенностью может привести к созданию сильного ИИ. Поэтому к Reinforcement Learning такой большой интерес в последние годы.
Конечно, лучше всего сильный ИИ создавать комбинируя все три подхода. На картинках и с обучением с подкреплением можно получить ИИ уровня животных. А добавив к картинкам текстовые названия объектов (шутка, конечно же — заставив ИИ просматривать видео, где люди взаимодействуют и разговаривают, как при обучении младенца), и дообучив на текстовом массиве для получения знаний (аналог нашей школы и университета), в теории можно получить ИИ человеческого уровня. Способный разговаривать.
У обучения с подкреплением есть один большой плюс. В симуляторе можно создать упрощенную модель мира. Так, для фигурки человека достаточно всего 17 степеней свободы, вместо 700 в живом человеке (примерное число мышц). Поэтому в симуляторе можно решать задачу в очень маленькой размерности.
Забегая вперед, современные алгоритмы Reinforcement Learning не способны произвольно управлять моделью человека даже с 17 степенями свободы. То есть не могут решить задачу оптимизации, где на входе 44 числа и на выходе 17. Удается это сделать только в очень простых случаях, с тонкой ручной настройкой начальных условий и гиперпараметров. И даже в этом случае, например чтобы научить модель гуманоида с 17 степенями свободы бегать, причем начиная с положения стоя (что намного проще), нужно несколько суток расчетов на мощном GPU. А чуть более сложные случаи, например научиться вставать из произвольной позы, может вообще никогда не обучиться. Это провал.
Кроме того, все Reinforcement Learning алгоритмы работают с удручающе маленькими нейронными сетями, а с обучением больших не справляются. Крупные сверточные сети используются только чтобы снизить размерность картинки до нескольких features, которые и подаются на вход алгоритмам обучения с подкреплением. Тот же бегающий гуманоид управляется Feed Forward сетью с двумя-тремя слоями по 128 нейронов. Серьезно? И на основе этого мы пытаемся построить сильный ИИ?
Чтобы попытаться понять, почему так происходит и что не так с обучением с подкреплением, надо сначала ознакомиться с основными архитектурами в современном Reinforcement Learning.
Физическое устройство мозга и нервной системы настроено эволюцией под конкретный вид животного и его условия обитания. Так, у мухи в процессе эволюции развилась такая нервная система и такая работа нейромедиаторов в ганглиях (аналог мозга у насекомых), чтобы быстро уворачиваться от мухобойки. Ну хорошо, не от мухобойки, а от птиц, которые их ловили 400 миллионов лет (шутка, птицы сами появились 150 млн лет назад, скорее от лягушек 360 млн лет). А носорогу достаточно такой нервной системы и мозга, чтобы медленно повернуться в сторону цели и начать бежать. А там, как говорится, у носорога плохое зрение, но это уже не его проблемы.
Но помимо эволюции, у каждой конкретной особи, начиная с рождения и в течении всей жизни, работает именно обычный механизм обучения с подкреплением. В случае млекопитающих, да и насекомых тоже, эту работу выполняет дофаминовая система. Ее работа полна тайн и нюансов, но все сводится к тому, что в случае получения награды, дофаминовая система, через механизмы памяти, как-то закрепляет связи между нейронами, которые были активны непосредственно до этого. Так формируется ассоциативная память.
Которая, в силу своей ассоциативности, потом используется при принятии решений. Проще говоря, если текущая ситуация (текущие активные нейроны в этой ситуации) по ассоциативной памяти активируют нейроны памяти об удовольствии, то особь выбирает действия, которые она делала в похожей ситуации и которые запомнила. «Выбирает действия» — это плохое определение. Выбора нет. Просто активированные нейроны памяти об удовольствии, закрепленные дофаминовой системой для данной ситуации, автоматически активируют моторные нейроны, приводящие к сокращению мышц. Это если необходимо немедленное действие.
Искусственному обучению с подкреплением, как области знаний, необходимо решить обе эти задачи:
1. Подобрать архитектуру нейросети (что для нас уже сделала эволюция)
Хорошая новость в том, что высшие когнитивные функции, выполняющиеся в неокортексе у млекопитающих (и в полосатом теле у врановых), выполняются в примерно однородной структуре. Видимо, для этого не нужно какой-то жестко прописанной «архитектуры».
Разноплановость областей мозга, вероятно, объясняется чисто историческими причинами. Когда по мере эволюции новые части мозга нарастали поверх базовых, оставшихся от самых первых животных. По принципу работает — не трогай. С другой стороны, у разных людей одинаковые части мозга реагируют на одинаковые ситуации. Это может объясняться как ассоциативностью (features и «нейроны бабушки» естественным образом сформировались в этих местах в процессе обучения), так и физиологией. Что сигнальные пути, закодированные в генах, ведут именно к этим областям. Единого мнения тут нет, но можно почитать, например, эту недавнюю статью: «Biological and artificial intelligence».
2. Научиться обучать нейронные сети по принципам обучения с подкреплением
Именно этим, в основном, и занимается современный Reinforcement Learning. И какие успехи? Не очень.
Наивный подход
Казалось бы, обучать нейросеть с подкреплением очень просто: делаем случайные действия, и если получили награду, то считаем сделанные действия «эталонными». Ставим их на выход нейросети как стандартные labels и обучаем нейронную сеть методом обратного распространения ошибки, чтобы она выдавала именно такой выход. Ну, самое обычное обучение нейросети. А если действия привели к неудаче, то либо игнорируем этот случай, либо подавляем эти действия (ставим эталонными на выходе какие-нибудь другие, например любое другое случайное действие). В общем и целом, эта идея повторяет дофаминовую систему.
Но если вы попробуете так обучать любую нейронную сеть, неважно насколько сложной архитектуры, реккурентную, сверточную или обычную прямого распространения, то… Ничего не выйдет!
Считается, что полезный сигнал настолько мал, что теряется на фоне шума. Поэтому стандартным методом обратного распространения ошибки сеть не обучается. Награда случается очень редко, может один раз из сотен или даже тысяч шагов. А даже LSTM запоминает максимум 100-500 точек истории, и то лишь в очень простых задачах. А на более сложных если будет 10-20 точек истории, то уже хорошо.
Но корень проблемы именно в очень редких наградах (по крайней мере в задачах, представляющих практическую ценность). На данный момент мы не умеем обучать нейросети, которые запоминали бы единичные случаи. С чем мозг справляется с блеском. Можно что-то, случившееся всего один раз, запомнить на всю жизнь. И, кстати, большая часть обучения и работы интеллекта строится именно на таких случаях.
Это что-то вроде жуткого дисбаланса классов из области распознавания изображений. Способов бороться с этим просто нет. Лучшее, что пока смогли придумать — это просто подавать на вход сети наравне с новыми ситуациями, сохраненные в искусственном специальном буфере удачные ситуации из прошлого. То есть, постоянно обучать не только новым случаям, но и удачным старым. Естественно, нельзя бесконечно увеличивать такой буфер, да и непонятно что именно в нем хранить. Еще пытаются как-то на время фиксировать пути внутри нейросети, бывшие активными во время удачного случая, чтобы последующее обучение их не перезаписывало. Довольно близкая аналогия к происходящему в мозге, на мой взгляд, хотя особых успехов в этом направлении тоже пока не добились. Так как новые обученные задачи в своем расчете используют и результаты выхода нейронов из замороженных путей, то в итоге сигнал только по этим замороженным интерферирует с новыми, и старые задачи перестают работать. Есть еще один любопытный подход: обучать сеть новым примерам/задачам только в ортогональном направлении к предыдущим задачам (https://arxiv.org/abs/1810.01256). Это не перезаписывает предыдущий опыт, но резко ограничивает емкость сети.
Отдельным классом алгоритмов, призванных бороться с этой бедой (а заодно дарящих надежду достичь сильного ИИ), идут разработки в Meta-Learning. Это попытки обучить нейросеть сразу нескольким задачам. Не в смысле, что распознавать разные картинки в одной задаче, а именно разным задачам в разных доменах (каждый со своим распределением и ландшафтом решений). Скажем, распознавать картинки и одновременно ездить на велосипеде. Успехи пока тоже не очень, так как обычно все сводится к тому, чтобы заранее подготовить нейросеть с общими универсальными весами, а потом быстро, всего за несколько шагов градиентного спуска, доадаптировать их к конкретной задаче. Примеры алгоритмов метаобучения — MAML и Reptile.
В общем, только эта проблема (невозможность учиться на единичных удачных примерах) ставит крест на современном обучении с подкреплением. Вся мощь нейросетей перед этим печальным фактом пока бессильна.
Этот факт, что самый простой и очевидный способ не работает, заставил исследователей вернуться к классическому табличному Reinforcement Learning. Который как наука появился еще в седой древности, когда нейросети не были даже в проекте. Но теперь, вместо ручного подсчета значений в таблицах и в формулах, давайте в качестве целевых функций использовать такой мощный аппроксиматор, как нейронные сети! В этом вся суть современного Reinforcement Learning. И главное его отличие от обычного обучения нейросетей.
Q-learning и DQN
Reinforcement Learning (еще до нейросетей) зародился как довольно простая и оригинальная идея: давайте делать, опять же, случайные действия, а потом для каждой ячейки в таблице и каждого направления движения, посчитаем по специальной формуле (получившей название уравнение Беллмана, это слово вы будете встречать практически в каждой работе по обучению с подкреплением), насколько хороша эта ячейка и выбранное направление. Чем выше получится это число, тем с большей вероятностью этот путь ведет к победе.
В какой ячейке вы бы ни появились, двигайтесь по нарастанию зеленого цвета! (в сторону максимального числа по бокам текущей ячейки).
Это число получило название Q (от слова quality — качество выбора, очевидно), а метод — Q-learning. Заменив формулу расчета этого числа на нейронную сеть, а точнее обучая нейронную сеть по этой формуле (плюс еще пара трюков, связанных чисто с математикой обучения нейросетей), в Deepmind получили метод DQN. Это который в 2015 году победил в куче Atari игр и положил начало революции в Deep Reinforcement Learning.
К сожалению, этот метод по своей архитектуре работает только с дискретными discrete действиями. В DQN на вход нейросети подается текущий state (текущая ситуация), а на выходе нейросеть предсказывает число Q. А так как на выходе сети перечислены сразу все возможные действия (каждый со своим предсказанным Q), то получается что нейросеть в DQN реализует классическую функцию Q(s,a) из Q-learning. Выдает Q для state и action (поэтому обозначение Q(s,a) как функции от s и a). Мы просто ищем обычным argmax по массиву среди выходов сети ячейку с максимальным числом Q и делаем действие, которое соответствует индексу этой ячейки.
Причем можно всегда выбирать действие с максимальным Q, тогда такая политика будет называться детерменистской. А можно выбирать действие как случайное из доступных, но пропорционально их Q-значениям (т.е. действия с высоким Q будут выбираться чаще, чем с низким). Такая политика называется стохастическая. У стохастического выбора плюс в том, что автоматически реализуется поиск и исследование мира (Exploration), так как каждый раз выбираются разные действия, иногда не кажущиеся самыми оптимальными, но могущие в будущем привести к большой награде. И тогда мы обучимся и повысим этим действиям вероятность, чтобы теперь они чаще выбирались согласно их вероятности.
В дальнейшем было разработано много оригинальных и местами гениальных алгоритмов на основе DQN, позволивших, в том числе, работать с continuous действиями (за счет хитростей и введения дополнительных нейросетей): DDQN, DuDQN, BDQN, CDQN, NAF, Rainbow. Пожалуй, сюда можно также отнести Direct Future Prediction (DFP), который роднится с DQN архитектурой сети и дискретными действиями. Вместо предсказания числа Q для всех действий, DFP напрямую предсказывает сколько на следующем шаге будет здоровья или патронов, если выбрать это действие. Причем на один шаг вперед и на несколько шагов вперед. Нам остается лишь перебрать все выходы сети и найти максимальное значение интересующего нас параметра и выбрать соответствующее этому элементу массива действие, в зависимости от текущих приоритетов. Например, если мы ранены, то можем среди выходов сети искать действие, ведущее к максимальному увеличению здоровья.
Но что еще важнее, за последующее время были разработаны новые архитектуры специально для Reinforcement Learning.
Policy Gradient
Давайте на вход сети подавать текущий state, а на выходе сразу предсказывать действия (либо сами действия, либо распределение вероятностей для них в стохастической политике). Мы просто действуем, применяя actions, предсказанные нейросетью. А потом смотрим, какую награду R набрали за эпизод. Эта награда может быть либо выше начальной (когда выиграли в игре), либо ниже (проиграли в игре). Также можно награду сравнивать со некоей средней наградой. Выше она средней или ниже.
Собственно, динамику полученной награды R в результате действий, которые подсказала нейросеть, можно использовать для вычисления градиента по специальной формуле. И применить этот градиент к весам нейросети! И дальше использовать обычное обратное распространение ошибки. Просто вместо «эталонных» действий на выходе сети в качестве labels (мы ведь не знаем какие они должны быть), используем изменение награды для расчета градиента. По этому градиенту сеть обучится, чтобы предсказывать действия, которые ведут к увеличению награды R.
Это классический Policy Gradient. Но у него есть недостаток — надо ждать окончания эпизода, чтобы посчитать куммулятивную награду R, прежде чем изменять веса сети согласно ее изменению. А из преимуществ — гибкая система поощрений и наказаний, которая не только работает в обе стороны, но также зависит от величины награды. Большая награда сильнее поощряет действия, которые к ней привели.
Actor-critic, DDPG
А теперь представьте, что у нас есть две сети — одна предсказывает какие действия надо совершить, а вторая оценивает насколько эти действия хороши. То есть, выдает Q-число для этих действий, как в алгоритме DQN. На вход первой сети подается state, а она предсказывает action(s). Вторая сеть на вход тоже получает state, но еще и действия action, предсказанные первой сетью, а на выходе выдает число Q как функцию от них обоих: Q(s,a).
Собственно, это число Q(s,a), выданное второй сетью (ее называют critic, критик), точно также можно использовать для вычисления градиента, которым обновлять веса первой сети (которую называют актером, actor), как мы делали выше с наградой R. Ну а вторая сеть обновляется обычным путем, согласно реальному прохождению эпизода. Этот метод получил название actor-critic. Его плюс по сравнению с классическим Policy Gradient, что веса сети можно обновлять на каждом шаге, не дожидаясь окончания эпизода. Что ускоряет обучение.
В таком виде это сеть DDPG. Так как она предсказывает напрямую действия actions, то прекрасно работает с continuous действиями. DDPG является прямым continuous конкурентом DQN с его дискретными действиями.
Advantage Actor Critic (A3C/A2C)
Следующим шагом стало использование для обучения первой сети не просто предсказания критиком critic числа Q(s,a) — насколько хороши действия, предсказанные актером actor, как это было в DDPG. А насколько эти предсказанные действия оказались лучше или хуже, чем мы ожидали.
Это очень близко к тому, что происходит в биологическом мозге. Из экспериментов известно, что максимальный выброс дофамина происходит не во время самого получения удовольствия, а во время ожидания, что скоро получим удовольствие. Впрочем, если ожидания не оправдались, то наступают ужасные последствия, большие чем в обычном случае (в организме присутствует специальная система наказания, обратная системе вознаграждения).
Для этого для расчета градиентов стали использовать не число Q(s,a), а так называемое Advantage: A(s,a) = Q(s,a) — V(s). Число A(s,a) показывает не абсолютное качество Q(s,a) выбранных действий, а относительное преимущество — насколько после предпринятых действий станет лучше, чем текущая ситуация V(s). Если A(s,a) > 0, то градиент будет изменять веса нейросети, поощряя предсказанные сетью действия. Если A(s,a)