в чем заключается процесс обучения алгоритма k ближайших соседей
Классификатор kNN
kNN расшифровывается как k Nearest Neighbor или k Ближайших Соседей — это один из самых простых алгоритмов классификации, также иногда используемый в задачах регрессии. Благодаря своей простоте, он является хорошим примером, с которого можно начать знакомство с областью Machine Learning. В данной статье рассмотрен пример написания кода такого классификатора на python, а также визуализация полученных результатов.
Задача классификации в машинном обучении — это задача отнесения объекта к одному из заранее определенных классов на основании его формализованных признаков. Каждый из объектов в этой задаче представляется в виде вектора в N-мерном пространстве, каждое измерение в котором представляет собой описание одного из признаков объекта. Допустим нам нужно классифицировать мониторы: измерениями в нашем пространстве параметров будут величина диагонали в дюймах, соотношение сторон, максимальное разрешение, наличие HDMI-интерфейса, стоимость и др. Случай классификации текстов несколько сложнее, для них обычно используется матрица термин-документ (описание на machinelearning.ru).
Для обучения классификатора необходимо иметь набор объектов, для которых заранее определены классы. Это множество называется обучающей выборкой, её разметка производится вручную, с привлечением специалистов в исследуемой области. Например, в задаче Detecting Insults in Social Commentary для заранее собранных тестов комментариев человеком проставлено мнение, является ли этот комментарий оскорблением одного из участников дискуссии, само же задание является примером бинарной классификации. В задаче классификации может быть более двух классов (многоклассовая), каждый из объектов может принадлежать более чем к одному классу (пересекающаяся).
Алгоритм
Исходные данные
Рассмотрим работу классификатора на примере. Для начала, нам нужно сгенерировать данные, на которых будут производиться эксперименты:
Для простоты я выбрал двумерное пространство, в котором случайным образом на участке от 0 до 5 по каждой из осей выбирается местоположение мат.ожидания двумерного гауссиана со среднеквадратичным отклонением 0.5. Значение 0.5 выбрано, чтобы объекты оказались достаточно хорошо разделимыми (правило трех сигм).
Чтобы посмотреть на полученную выборку, нужно выполнить следующий код:
Вот пример полученного в результате выполнения этого кода изображения:
Получение обучающей и тестовой выборки
Итак, у нас имеется набор объектов, для каждого из которых задан класс. Теперь нам нужно разбить это множество на две части: обучающую выбору и тестовую выборку. Для этого служит следующий код:
Реализация классификатора
Теперь, имея обучающую выборку, можно реализовать и сам алгоритм классификации:
Для определения расстояния между объектами можно использовать не только евклидово расстояние: также применяются манхэттенское расстояние, косинусная мера, критерий корелляции Пирсона и др.
Примеры выполнения
Теперь можно оценить, насколько хорошо работает наш классификатор. Для этого сгенерируем данные, разобьем их на обучающую и тестовую выборку, произведем классификацию объектов тестовой выборки и сравним реальное значение класса с полученным в результате классификации:
Для оценки качества работы классификатора используются различные алгоритмы и различные меры, более подробно можно почитать здесь: wiki
Теперь осталось самое интересное: показать работу классификатора графически. В приведенных ниже картинках я использовал 3 класса, в каждом по 40 элементов, значение k для алгоритма взял равным трем.
Для вывода этих картинок использован следующий код:
Заключение
kNN — один из простейших алгоритмов классификации, поэтому на реальных задачах он зачастую оказывается неэффективным. Помимо точности классификации, проблемой этого классификатора является скорость классификации: если в обучающей выборке N объектов, в тестовой выборе M объектов, а размерность пространства — K, то количество операций для классификации тестовой выборки может быть оценено как O(K*M*N). И тем не менее, алгоритм работы kNN является хорошим примером для начала знакомства с Machine Learning.
Классификация данных методом k-ближайших соседей
Преимуществом статистических методов является их хорошая математическая обоснованность, недостатком — низкая объясняющая способность. Использование вероятностных оценок позволяет с высокой точностью предсказать к какому классу относится объект, но не позволяет сказать почему. Поэтому результаты статистических методов классификации могут оказаться сложными для понимания и интерпретации результатов.
Одной из важнейших задач анализа данных является классификация — отнесение объектов предметной области к заранее определённым группам, называемым классами. При этом каждому классу должны принадлежать объекты, близкие по своим свойствам. Обобщая свойства известных объектов класса на новые, отнесённые к нему объекты, можно получать знания о них.
Задача классификации решается с помощью аналитических моделей, называемых классификаторами. Классифицировать объект означает предъявить набор его признаков (обычно представленных в виде вектора) на вход модели-классификатора, которая должна присвоить ему метку или номер класса. В настоящее время разработано большое количество различных видов классификаторов, для построения которых используются как статистические методы (логистическая регрессия, дискриминантный анализ), так и методы машинного обучения (нейронные сети, деревья решений и др.).
Необходимость использования в анализе данных большого числа разнообразных методов классификации, обусловлена тем, что решаемые с её помощью задачи могут иметь свои особенности, связанные, например, с представлением исходных данных, их количеством и качеством, что требует выбора адекватного классификатора. Поэтому выбор классификатора, соответствующего особенностям решаемой задачи анализа, является важным фактором получения правильного решения.
Отнесение классификации к интеллектуальным технологиям анализа данных обусловлено тем, что в повседневной жизни сознание человека, в поле которого постоянно попадают новые объекты окружающего мира, сопоставляет их с уже известными объектами и оценивает степень их сходства. Затем, на основе это оценки объект ассоциируется с определённой группой (классом). Таким образом, классификация является наиболее «естественным» для человеческого интеллекта способом получения знаний о процессах и явлениях, происходящих в окружающем мире.
Учитывая сказанное, можно предположить, что все методы классификации в том или ином виде будут использовать формализованное понятие «сходства», мера которого будет оцениваться с помощью некоторой функции. В статистических методах анализа мерой сходства является вероятность принадлежности объекта классу, которая оценивается для каждого класса, после чего выбирается тот из них, для которого эта вероятность наибольшая.
В метрических методах мерой сходства является расстояние (например, евклидово) в векторном пространстве, где каждый объект представлен своим вектором признаков. Логика здесь проста: новый объект скорее всего принадлежит к тому же классу, что и большинство соседних с ним объектов. Метрические методы как правило используются для построения классификаторов на основе машинного обучения.
Преимуществом статистических методов является их хорошая математическая обоснованность, недостатком — низкая объясняющая способность. Использование вероятностных оценок позволяет с высокой точностью предсказать к какому классу относится объект, но не позволяет сказать почему. Поэтому результаты статистических методов классификации могут оказаться сложными для понимания и интерпретации результатов.
Недостатком метрических методов является их эвристический характер — они могут дать неточное и неоднозначное решение, но считающееся приемлемым в большинстве практически значимых случаев. Однако при этом они имеют высокую объясняющую способность и поэтому их результаты проще интерпретировать. В простейшем случае можно использовать правило: объект относится к тому же классу, что и большинство его ближайших соседей.
Типичным представителем методов классификации, использующих эту логику, является метод k-ближайших соседей — k-nearest neighbors algorithm (KNN). Метод был впервые разработан Эвелином Фиксом и Джозефом Лоусоном Ходжесом в 1951 году, и позднее развит Томасом Ковером.
Метод относится к классу непараметрических, т.е. не требует предположений о том, из какого статистического распределения была сформирована обучающее множество. Следовательно, классификационные модели, построенные с помощью метода KNN также будут непараметрическими. Это означает, что структура модели не задаётся жёстко изначально, а определяется данными.
Поскольку признаки, на основе которых производится классификация могут иметь различную физическую природу и, соответственно, диапазоны значений, для улучшения результатов классификации будет полезно выполнить нормализацию обучающих данных.
Алгоритм
На фазе классификации предъявляется новый объект, для которого метка класса не задана. Для него определяются k ближайших (в смысле некоторой метрики) предварительно классифицированных наблюдений. Затем выбирается класс, которому принадлежит большинство из k ближайших примеров-соседей, и к этому же классу относится классифицируемый объект.
Поясним работу алгоритма с помощью рисунка.
Рисунок 1 – Работа алгоритма KNN
Определение класса нового объекта
В простейшем случае класс нового объекта может быть определён простым выбором наиболее часто встречающегося класса среди k примеров. Однако на практике это не всегда удачное решение, например, в случае когда частота появления для двух или более классов оказывается одинаковой. Кроме этого разумно предположить, что не все обучающие имеют одинаковую значимость для определения класса. В этом случае используют некоторую функцию, с помощью которой определяется класс, называемую функцией сочетания (combination function).
В обычном случае используют так называемое простое невзвешенное голосование (simple unweighted voting). При это предполагается, что все k примеров имеют одинаковое право «голоса» независимо от расстояние до классифицируемого объекта.
Однако, логично предположить, что чем дальше пример расположен от классифицируемого объекта в пространстве признаков, тем ниже его значимость для определения класса. Поэтому для улучшения результатов классификации вводят взвешивание примеров в зависимости от их удалённости. В этом случае используют взвешенное голосование (weighted voting).
Выбор значения параметра k
Кроме этого, следует учитывать, что использование небольших значений k увеличивает влияние шумов на результаты классификации, когда небольшие изменения в данных приводят к большим изменениям в результатах классификации. Но при этом границы классов оказываются более выраженными (класс при голосовании побеждает с большим счётом).
Напротив, если значение параметра слишком велико, то в процессе классификации принимает участие много объектов, относящихся к разным классам. Такая классификация оказывается слишком грубой и плохо отражает локальные особенности набора данных. Таким образом, выбор параметра k является компромиссом между точностью и обобщающей способностью модели.
При больших значениях параметра k уменьшается зашумленность результатов классификации, но снижается выраженность границ классов.
В задачах бинарной классификации бывает целесообразно выбрать k как нечетное число, так как это позволяет избежать равенства «голосов» при определении класса для нового наблюдения.
Особенности работы алгоритма
Если значения признаков непрерывные, то в качестве меры расстояния между объектами обычно используется расстояние Евклида, а если категориальные, то может использоваться расстояние Хэмминга.
Алгоритма KNN является чувствительным к дисбалансу классов в обучающих данных: алгоритм «склонен» к смещению решения в сторону доминирующего класса, поскольку относящиеся к нему объекты просто чаще попадают в число ближайших соседей. Одним из способов решения данной проблемы является применение различных способов взвешивания при «голосовании».
Рисунок 2 – Обратное соседство
Ещё одной проблемой алгоритма KNN, характерной, впрочем, и для большинства методов классификации, является различная значимость признаков с точки зрения определения класса объектов. Учет фактора значимости признаков в алгоритме может позволить повысить точность классификации.
Для этого аналитик или эксперт на основе субъективной, либо некоторой формальной оценки может задать уровень значимости признака, выразив его с помощью числового коэффициента (обозначим его s от англ significance — значимость), который учитывается при вычислении расстояния между примерами и классифицируемым объектом:
Численный пример
Рассмотрим простой численный пример работы алгоритма KNN, проиллюстрированный на рисунке 3.
Рисунок 3 – Численный пример
Пусть имеется набор данных о заёмщиках банка часть из которых допустили просрочку по платежу (таблица 1). Признаками являются возраст и среднемесячный доход. Метками класса в поле «Просрочено» будут «Да» и «Нет».
На рисунке 3 оранжевыми кружками представлены объекты класса «Нет», а фиолетовыми класса «Да». Синим квадратом отображается классифицируемый объект (новый заёмщик).
Задача заключается в том, чтобы выполнить классификацию нового заёмщика для которого A_1=42 и A_2=34 с целью оценить возможность просрочки им платежей.
Таким образом, из трёх ближайших соседей (на рисунке расположены внутри круга) классифицируемого объекта два имеют класс «Да», а один — «Нет». Следовательно, путём простого невзвешенного голосования определяем его класс как «Да». На основании работы классификатора делаем вывод, что заёмщик с заданными характеристиками может допустить просрочку по выплате кредита.
Области применения алгоритма
Алгоритм KNN может применяться практически во всех задачах классификации, особенно в тех случаях, когда оценить параметры вероятностного распределения данных сложно или невозможно. Наиболее типичными приложениями алгоритма KNN являются:
Достоинства и недостатки алгоритма
В заключение отметим достоинства и недостатки алгоритма KNN. К достоинствам алгоритма можно отнести.
К недостаткам алгоритм KNN можно отнести:
🤖 Метод k-ближайших соседей (k-nearest neighbour)
Пример классификации k-ближайших соседей.
Теоретическая составляющая алгоритма k-NN
Помимо простого объяснения, необходимо понимание основных математических составляющих алгоритма k-ближайших соседей.
Формула вычисления Евклидова расстояния:
MinMax-нормализация осуществляется следующим образом:
в данном случае все значения будут находиться в диапазоне от 0 до 1; дискретные бинарные значения определяются как 0 и 1.
где σ – среднеквадратичное отклонение. В данном случае большинство значений попадает в диапазон.
Каков порядок действий?
Реализация на языке Python
Набор данных состоит из 15 столбцов, таких как sex (пол), fare (плата за проезд), p_class (класс каюты), family_size (размер семьи), и т. д. Главным признаком, который мы и должны предсказать в соревновании, является survived (выжил пассажир или нет).
Дополнительный анализ показал, что находящиеся в браке люди имеют больший шанс на то, чтобы быть спасенными с корабля. Поэтому были добавлены еще 4 столбца, переименованные из Name (Имя), которые обозначают мужчин и женщин в зависимости от того, были они женаты или нет (Mr, Mrs, Mister, Miss).
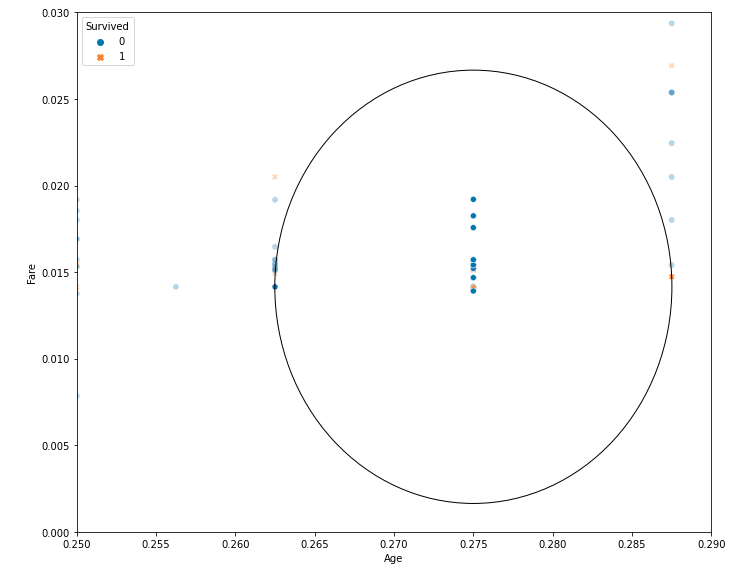
Чтобы наглядно продемонстрировать функциональность k-NN для предсказания выживания пассажира, мы рассматриваем только два признака: age (возраст), fare (плата за проезд).
Здесь вероятность выживания составляет 0.3 – 30%.
Результат работы кода:
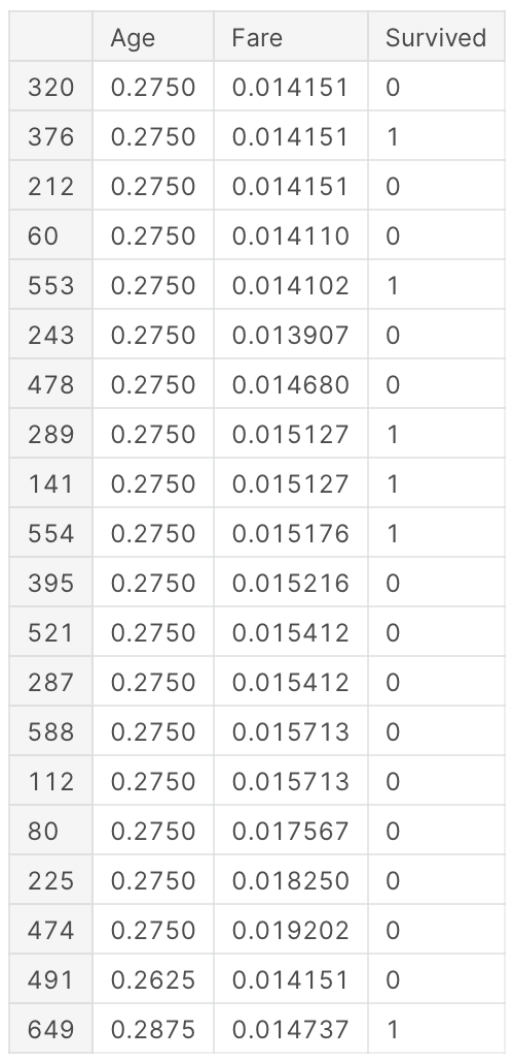
Как видите, на графике показаны 20 ближайших соседей, 14 из которых связаны с теми, кто не выжил (вероятность 0,7 – 70%), а 6 связаны с выжившими (вероятность 0,3 – 30%).
Мы можем просмотреть первые 20 ближайших соседей для заданных параметров при помощью следующего кода:
Результатом будет таким:
Выбор Оптимального значения для k-NN
Не существует конкретного способа определить наилучшее значение для k, поэтому нам нужно попробовать несколько значений, чтобы найти лучшее из них. Но чаще всего наиболее предпочтительным значением для k является 5:
Преимущества и Недостатки
В заключение
Метод k-ближайших соседей (k-nearest neighbors) – это простой алгоритм машинного обучения с учителем, который можно использовать для решения задач классификации и регрессии. Он прост в реализации и понимании, но имеет существенный недостаток – значительное замедление работы, когда объем данных растет.
Алгоритмы K-ближайших соседей и K-средних на Python
Одно из самых популярных приложений машинного обучения — решение задач классификации. Задачи классификации — это ситуации, когда у вас есть набор данных, и вы хотите классифицировать наблюдения из этого набора в определенную категорию.
Известный пример — спам-фильтр для электронной почты. Gmail использует методы машинного обучения с учителем, чтобы автоматически помещать электронные письма в папку для спама в зависимости от их содержания, темы и других характеристик.
Две модели машинного обучения выполняют большую часть работы, когда дело доходит до задач классификации:
Из этого руководства вы узнаете, как применять алгоритмы K-ближайших соседей и K-средних в коде на Python.
Модели K-ближайших соседей
Алгоритм K-ближайших соседей является одним из самых популярных среди ML-моделей для решения задач классификации.
Обычным упражнением для студентов, изучающих машинное обучение, является применение алгоритма K-ближайших соседей к датасету, категории которого неизвестны. Реальным примером такой ситуации может быть случай, когда вам нужно делать предсказания, используя ML-модели, обученные на секретных правительственных данных.
В этом руководстве вы изучите алгоритм машинного обучения K-ближайших соседей и напишите его реализацию на Python. Мы будем работать с анонимным набором данных, как в описанной выше ситуации.
Используемый датасет
Первое, что вам нужно сделать, это скачать набор данных, который мы будем использовать в этом руководстве. Вы можете скачать его на Gitlab.
Далее вам нужно переместить загруженный файл с датасетом в рабочий каталог. После этого откройте Jupyter Notebook — теперь мы можем приступить к написанию кода на Python!
Необходимые библиотеки
Чтобы написать алгоритм K-ближайших соседей, мы воспользуемся преимуществами многих Python-библиотек с открытым исходным кодом, включая NumPy, pandas и scikit-learn.
Начните работу, добавив следующие инструкции импорта:
Импорт датасета
Следующий шаг — добавление файла classified_data.csv в наш код на Python. Библиотека pandas позволяет довольно просто импортировать данные в DataFrame.
Поскольку датасет хранится в файле csv, мы будем использовать метод read_csv :
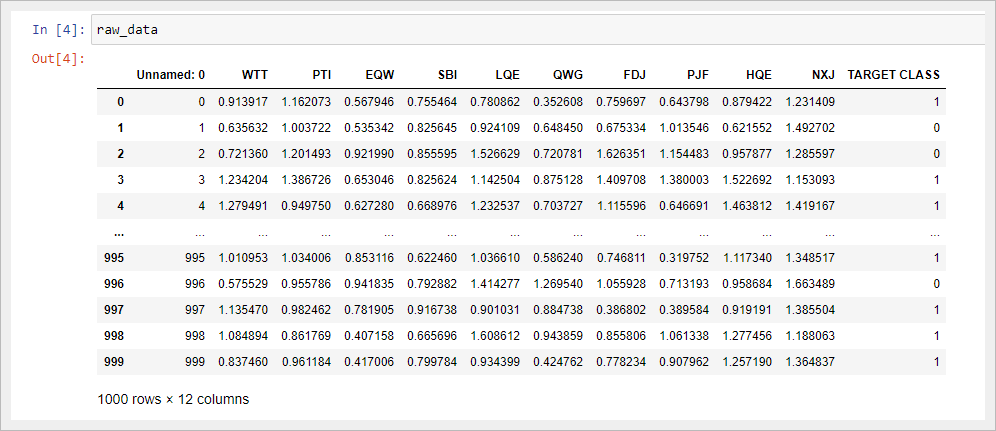
Отобразив полученный DataFrame в Jupyter Notebook, вы увидите, что представляют собой наши данные:
Стоит заметить, что таблица начинается с безымянного столбца, значения которого равны номерам строк DataFrame. Мы можем исправить это, немного изменив команду, которая импортировала наш набор данных в скрипт Python:
Затем давайте посмотрим на показатели (признаки), содержащиеся в этом датасете. Вы можете вывести список имен столбцов с помощью следующей инструкции:
Поскольку этот набор содержит секретные данные, мы понятия не имеем, что означает любой из этих столбцов. На данный момент достаточно признать, что каждый столбец является числовым по своей природе и поэтому хорошо подходит для моделирования с помощью методов машинного обучения.
Стандартизация датасета
Поскольку алгоритм K-ближайших соседей делает прогнозы относительно точки данных (семпла), используя наиболее близкие к ней наблюдения, существующий масштаб показателей в датасете имеет большое значение.
Из-за этого специалисты по машинному обучению обычно стандартизируют набор данных, что означает корректировку каждого значения x так, чтобы они находились примерно в одном диапазоне.
К счастью, библиотека scikit-learn позволяет сделать это без особых проблем.
Для начала нам нужно будет импортировать класс StandardScaler из scikit-learn. Для этого добавьте в свой скрипт Python следующую команду:
Во-первых, давайте создадим экземпляр класса StandardScaler с именем scaler следующей инструкцией:
Теперь мы можем обучить scaler на нашем датасете, используя метод fit:
Теперь мы можем применить метод transform для стандартизации всех признаков, чтобы они имели примерно одинаковый масштаб. Мы сохраним преобразованные семплы в переменной scaled_features :
В качестве результата мы получили массив NumPy со всеми точками данных из датасета, но нам желательно преобразовать его в формат DataFrame библиотеки pandas.
К счастью, сделать это довольно легко. Мы просто обернем переменную scaled_features в метод pd.DataFrame и назначим этот DataFrame новой переменной scaled_data с соответствующим аргументом для указания имен столбцов:
Теперь, когда мы импортировали наш датасет и стандартизировали его показатели, мы готовы разделить этот набор данных на обучающую и тестовую выборки.
Разделение датасета на обучающие и тестовые данные
Мы будем использовать функцию train_test_split библиотеки scikit-learn в сочетании с распаковкой списка для создания обучающих и тестовых датасетов из нашего набора секретных данных.
Во-первых, вам нужно импортировать train_test_split из модуля model_validation библиотеки scikit-learn:
Вы можете создать эти переменные следующим образом:
Теперь, когда наш датасет разделен на данные для обучения и данные для тестирования, мы готовы приступить к обучению нашей модели!
Обучение модели K-ближайших соседей
Начнем с импорта KNeighborsClassifier из scikit-learn:
Теперь мы можем обучить нашу модель, используя метод fit и переменные x_training_data и y_training_data :
Теперь давайте сделаем несколько прогнозов с помощью полученной модели!
Делаем предсказания с помощью алгоритма K-ближайших соседей
В частности, вот так вы можете делать предсказания и присваивать их переменной predictions :
Давайте посмотрим, насколько точны наши прогнозы, в следующем разделе этого руководства.
Оценка точности нашей модели
В руководстве по логистической регрессии мы видели, что scikit-learn поставляется со встроенными функциями, которые упрощают измерение эффективности классификационных моделей машинного обучения.
Для начала импортируем в наш отчет две функции classification_report и confusion_matrix :
Точно так же вы можете сгенерировать матрицу ошибок:
Глядя на такие метрики производительности, похоже, что наша модель уже достаточно эффективна. Но ее еще можно улучшить.
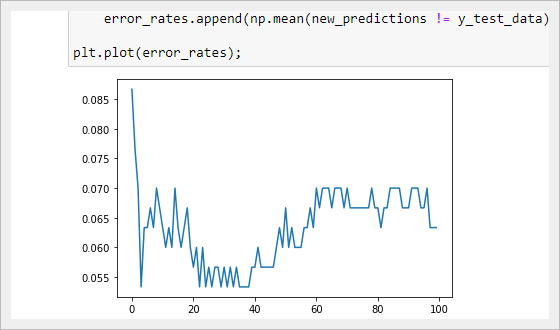
Выбор оптимального значения для K с помощью метода «Локтя»
В этом разделе мы будем использовать метод «локтя», чтобы выбрать оптимальное значение K для нашего алгоритма K-ближайших соседей.
Метод локтя включает в себя итерацию по различным значениям K и выбор значения с наименьшей частотой ошибок при применении к нашим тестовым данным.
Реализация описанного цикла для значений K от 1 до 100:
Модели кластеризации методом K-средних
Алгоритм кластеризации K-средних обычно является первой моделью машинного обучения без учителя, которую изучают студенты.
Он позволяет специалистам по машинному обучению создавать группы точек данных со схожими количественными характеристиками в датасете. Это полезно для решения таких задач, как формирование клиентских сегментов или определение городских районов с высоким уровнем преступности.
В этом разделе вы узнаете, как создать свой первый алгоритм кластеризации K-средних на Python.
Используемый датасет
В этом руководстве мы будем использовать набор данных, созданный с помощью scikit-learn.
Давайте импортируем функцию make_blobs из scikit-learn, чтобы сгенерировать необходимые данные. Откройте Jupyter Notebook и запустите свой скрипт Python со следующей инструкцией:
В частности, вот как вы можете создать набор данных из 200 семплов, который имеет 2 показателя и 4 кластерных центров. Стандартное отклонение для каждого кластера будет равно 1.8.
Теперь, когда наши данные созданы, мы можем перейти к импорту других необходимых библиотек с открытым исходным кодом в наш скрипт Python.
Импортируемые библиотеки
В этом руководстве будет использоваться ряд популярных библиотек Python с открытым исходным кодом, включая pandas, NumPy и matplotlib. Продолжим написание скрипта, добавив следующие импорты:
Первая группа библиотек в этом блоке кода предназначена для работы с большими наборами данных. Вторая группа предназначена для визуализации результатов.
Теперь перейдем к созданию визуального представления нашего датасета.
Визуализация датасета
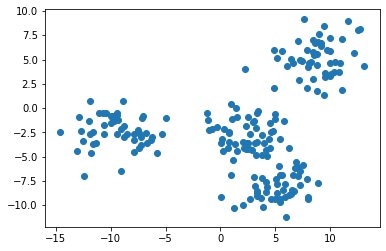
В функции make_blobs мы указали, что в нашем наборе данных должно быть 4 кластерных центра. Лучший способ убедиться, что все действительно так, — это создать несколько простых точечных диаграмм.
Примечание: ваш датасет будет отличаться от моего, поскольку его данные сгенерированы случайным образом.
Представленное изображение, похоже, указывает на то, что в нашем датасете всего три кластера. Нам так кажется потому, что два кластера расположены очень близко друг к другу.
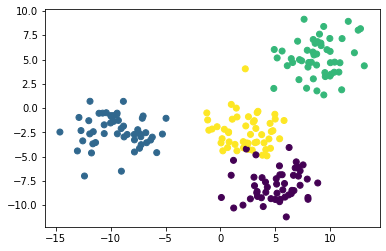
Если при построении мы будем использовать уникальный цвет для каждого кластера, то мы легко различим 4 группы наблюдений. Вот код для этого:
Теперь мы видим, что в нашем наборе данных есть четыре уникальных кластера. Давайте перейдем к построению нашей модели на основе метода K-средних на Python!
Создание и обучение модели кластеризации K-средних
Для того, чтобы начать использовать метод K-средних, импортируем соответствующий класс из scikit-learn. Для этого добавьте в свой скрипт следующую команду:
Затем давайте создадим экземпляр класса KMeans с параметром n_clusters=4 и присвоим его переменной model :
Теперь обучим нашу модель, вызвав на ней метод fit и передав первый элемент нашего кортежа raw_data :
В следующем разделе мы рассмотрим, как делать прогнозы с помощью модели кластеризации K-средних.
Прежде чем двигаться дальше, я хотел бы указать на одно различие, которое вы, возможно заметили, между процессом построения модели, используя метод K-средних (он является алгоритмом кластеризации без учителя), и алгоритмами машинного обучения с учителем, с которыми мы работали ранее в данном курсе.
Оно заключается в том, что нам не нужно разбивать набор данных на обучающую и тестовую выборки. Это важное различие, так как вам никогда не нужно разделять таким образом датасет при построении моделей машинного обучения без учителя!
Применяем нашу модель кластеризации K-средних для получения предсказаний
Специалисты по машинному обучению обычно используют алгоритмы кластеризации, чтобы делать два типа прогнозов:
Теперь, когда наша модель обучена, мы можем легко сгенерировать такие предсказания.
Во-первых, давайте предскажем, к какому кластеру принадлежит каждая точка данных. Для этого обратимся к атрибуту labels_ из объекта model с помощью оператора точки:
Таким образом мы получаем массив NumPy с прогнозами для каждого семпла:
Чтобы узнать, где находится центр каждого кластера, аналогичным способом обратитесь к атрибуту cluster_centers_ :
Получаем двумерный массив NumPy, содержащий координаты центра каждого кластера. Он будет выглядеть так:
Визуализация точности предсказаний модели
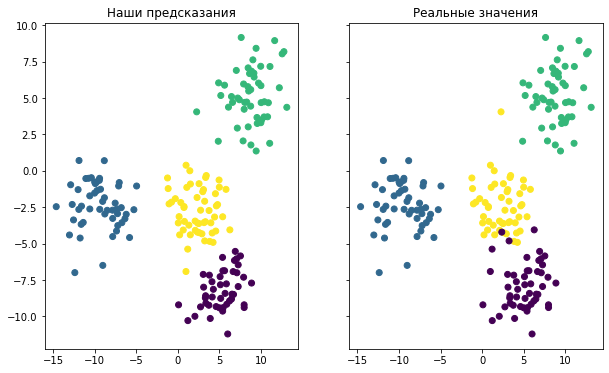
Последнее, что мы сделаем в этом руководстве, — это визуализируем точность нашей модели. Для этого можно использовать следующий код:
Он генерирует две точечные диаграммы. Первая показывает кластеры, используя фактические метки из нашего датасета, а вторая основана на предсказаниях, сделанных нашей моделью. Вот как выглядит результат:
Хотя окраска двух графиков разная, вы можете видеть, что созданная модель довольно хорошо справилась с предсказанием кластеров в нашем наборе данных. Вы также можете заметить, что модель не идеальна: точки данных, расположенные на краях кластеров, в некоторых случаях классифицируются неверно.
И последнее, о чем следует упомянуть, говоря об оценке точности нашей модели. В этом примере мы знали, к какому кластеру принадлежит каждое наблюдение, потому что мы сами создали этот набор данных.
Такая ситуация встречается крайне редко. Метод К-средних обычно применяется, когда не известны ни количество кластеров, ни присущие им качества. Таким образом, специалисты по машинному обучению используют данный алгоритм, чтобы обнаружить закономерности в датасете, о которых они еще ничего не знают.
Заключительные мысли
В этом руководстве вы научились создавать модели машинного обучения на Python, используя методы K-ближайших соседей и K-средних.
Вот краткое изложение того, что вы узнали о моделях K-ближайших соседей в Python:
А вот краткое изложение того, что вы узнали о моделях кластеризации K-средних в Python: