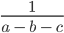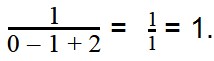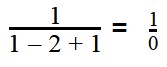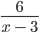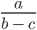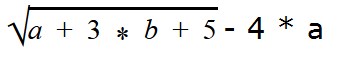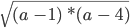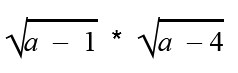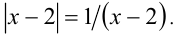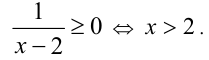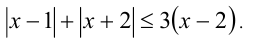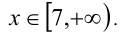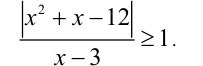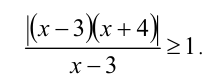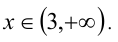Как находить одз с модулем
ОДЗ. Область допустимых значений (ЕГЭ 2022)
ОДЗ – это область допустимых значений, то есть это все значения переменной, при которых выражение имеет смысл.
Например, если перед тобой уравнение \( \displaystyle \sqrt
Часто в задачах бывает очень важно учесть ОДЗ и «вычеркнуть» те решения, которые на самом деле решениями не являются.
Иначе ты сделаешь глупую, очень глупую ошибку и не получишь то, что заслужил на ЕГЭ!
Читай эту статью и ты будешь знать об ОДЗ все!
ОДЗ — коротко о главном
ОДЗ – это область допустимых значений, то есть это все значения переменной, при которых выражение имеет смысл.
Функции, для которых важна ОДЗ:
ОДЗ (Область допустимых значений) — подробнее
Давай разберем пример, наглядно показывающий, что такое ОДЗ:
Решим уравнение \( \displaystyle \sqrt<2x+3>=x\).
Все очень просто, если ты уже освоил тему «Иррациональные уравнения».
Возводим левую и правую части уравнения в квадрат:
Теперь решаем квадратное уравнение. Я воспользуюсь теоремой Виета (если забыл, что это такое, – посмотри тему «Квадратные уравнения»).
Вроде все? А давай-ка теперь сделаем проверку – подставим полученные значения в начальное уравнение:
\( \displaystyle x=3:\text< >\sqrt<2\cdot 3+3>=3\text< >\Leftrightarrow \text< >\sqrt<9>=3\) – все верно.
Да потому, что мы не учли ОДЗ!
По определению квадратный корень из любого числа не может быть отрицательным.
Значит, глядя на уравнение \( \displaystyle \sqrt<2x+3>=x\) мы должны сразу же написать:
Если помнишь тему «Иррациональные уравнения», ты сразу скажешь, что второе условие в этой системе писать необязательно. И правда, мы ведь потом возведем все в квадрат, и получится, что \( \displaystyle 2x+3=<
Итак, с помощью этих рассуждений приходим к такой области допустимых значений:
\( \displaystyle x\ge 0\).
Тогда сразу становится ясно, что корень \( \displaystyle x=-1\) не подходит. И остается единственный ответ \( \displaystyle x=3\).
Всего мы изучаем несколько разных функций, для которых важна ОДЗ. Вот они со своими ОДЗ в удобной табличке.
Область допустимых значений функции
Допустимые и недопустимые значения переменных
В 7 классе заканчивается математика и начинается ее-величество-алгебра. Первым делом школьники изучают выражения с переменными.
Мы уже знаем, что математика состоит из выражений — буквенных и числовых. Каждому выражению, в котором есть переменная, соответствует область допустимых значений (ОДЗ). Если игнорировать ОДЗ, то в результате решения можно получить неверный ответ. Получается, чтобы быстро получить верный ответ, нужно всегда учитывать область допустимых значений.
Чтобы дать верное определение области допустимых значений, разберемся, что такое допустимые и недопустимые значения переменной.
Рассмотрим все необходимые определения, связанные с допустимыми и недопустимыми значениями переменной.
Выражение с переменными — это буквенное выражение, в котором буквы обозначают величины, принимающие различные значения.
Значение числового выражения — это число, которое получается после выполнения всех действий в числовом выражении.
Выражение с переменными имеет смысл при данных значениях переменных, если при этих значениях переменных можно вычислить его значение.
Выражение с переменными не имеет смысла при данных значениях переменных, если при этих значениях переменных нельзя вычислить его значение.
Теперь, опираясь на данные определения, мы можем сформулировать, что такое допустимые и недопустимые значения переменной.
Допустимые значения переменных — это значения переменных, при которых выражение имеет смысл.
Если при переменных выражение не имеет смысла, то значения таких переменных называют недопустимыми.
В выражении может быть больше одной переменной, поэтому допустимых и недопустимых значений может быть больше одного.
Пример 1
Рассмотрим выражение 
В выражении три переменные (a, b, c).
Запишем значения переменных в виде: a = 0, b = 1, c = 2.
Такие значения переменных являются допустимыми, поскольку при подстановке этих значений в выражение, мы легко можем найти ответ: 
Таким же образом можем выяснить, какие значения переменных — недопустимые.
Подставим значения переменных в выражение 
На ноль делить нельзя.
Что такое ОДЗ
ОДЗ — это невидимый инструмент при решении любого выражении с переменной. Чаще всего, ОДЗ не отображают графически, но всегда «держат в уме».
Область допустимых значений (ОДЗ) — это множество всех допустимых значений переменных для данного выражения.
Пример 2
Рассмотрим выражение 
Пример 3
Рассмотрим выражение 
ОДЗ такого выражения будет выглядеть вот так: b ≠ c; a — любое число.
Такая запись означает, что область допустимых значений переменных b, c и a = это все значения переменных, при которых соблюдаются условия b ≠ c; a — любое число.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).
Как найти ОДЗ: примеры решения
Найти ОДЗ — это значит, что нужно указать все допустимые значения переменных для выражения. Часто, чтобы найти ОДЗ, нужно выполнить преобразование выражения.
Чтобы быстро и верно определять ОДЗ, запомните условия, при которых значение выражения не может быть найдено.
Мы не можем вычислить значение выражения, если:
Теперь, приступая к поиску ОДЗ, вы можете сверять выражение по всем этим пунктам.
Давайте потренируемся находить ОДЗ.
Пример 4
Найдем область допустимых значений переменной выражения a 3 + 4 * a * b − 6.
В куб возводится любое число. Ограничений при вычитании и сложении нет. Это значит, что мы можем вычислить значение выражения a 3 + 4 * a * b − 6 при любых значениях переменной.
ОДЗ переменных a и b — это множество таких пар допустимых значений (a, b), где a — любое число и b — любое число.
Ответ: (a и b), где a — любое число и b — любое число.
Пример 5
Найдем область допустимых значений (ОДЗ) переменной выражения 
Здесь нужно обратить внимание на наличие нуля в знаменатели дроби. Одним из условий, при котором вычисление значения выражения невозможно явлется наличие деления на ноль.
Это значит, что мы может сказать, что ОДЗ переменной a в выражении 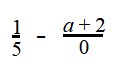— пустое множество.
Пустое множество изображается в виде вот такого символа Ø.
Пример 6
Найдем область допустимых значений (ОДЗ) переменных в выражении 
Если есть квадратный корень, то нам нужно следить за тем, чтобы под знаком корня не было отрицательного числа. Это значит, что при подстановке значений a и b должны быть условия, при которых a + 3 * b + 5 ≥ 0.
Ответ: ОДЗ переменных a и b — это множество всех пар, при которых a + 3 * b + 5 ≥ 0.
Запомните
Например, если х > 6, но х
Зачем учитывать ОДЗ при преобразовании выражения
Иногда выражение просто невозможно решить, если не выполнить ряд тождественных преобразований. К ним относятся: перестановки, раскрытие скобок, группировка, вынесение общего множителя за скобки, приведение подобных слагаемых.
Кроме того, что видов таких преобразований довольно много: нужно понимать, в каких случаях какое преобразование возможно. В этом может помочь определение ОДЗ.
Тождественное преобразование может:
Рассмотрим каждый случай в отдельности.
Пример 7
Поскольку мы должны следить за тем, чтобы в выражении не возникало деление на ноль, определяем условие a ≠ 0.
Это условие отвечает множеству (−∞ ; 0) ∪ (0 ; +∞).
В выражении есть подобные слагаемые, если привести подобные слагаемые, то мы получаем выражение вида a.
ОДЗ для a — это R — множество всех вещественных чисел.
Преобразование расширило ОДЗ — добавился ноль.
Пример 8
Рассмотрим выражение a 2 + a + 4 * a
ОДЗ a для этого выражения — множество R.
В выражении есть подобные слагаемые, выполним тождественное преобразование.
После приведения подобных слагаемых выражение приняло вид a 2 + 5 * a
ОДЗ переменной a для этого выражения — множество R.
Это значит, что тождественное преобразование никак не повлияло на ОДЗ.
Пример 9
Рассмотрим выражение 
Решить такое неравенство можно методом интервалов, что дает нам ОДЗ (−∞; 1] ∪ [4 ; +∞).
Затем выполним преобразование исходного выражения по свойству корней: корень произведения = произведению корней.
Приведем выражение к виду 
Решив систему линейных неравенств, получаем множество [4; + ∞).
Отсюда видно, что тождественные преобразования сузили ОДЗ.
От (−∞; 1] ∪ [4 ; +∞) до [4; + ∞).
Решив преобразовать выражение, внимательно следите за тем, чтобы не допустить сужение ОДЗ.
Запомните, что выполняя преобразование, следует выбирать такие, которые не изменят ОДЗ.
Область допустимых значений (ОДЗ): теория, примеры, решения
Любое выражение с переменной имеет свою область допустимых значений, где оно существует. ОДЗ необходимо всегда учитывать при решении. При его отсутствии можно получить неверный результат.
В данной статье будет показано, как правильно находить ОДЗ, использовать на примерах. Также будет рассмотрена важность указания ОДЗ при решении.
Допустимые и недопустимые значения переменных
Данное определение связано с допустимыми значениями переменной. При введении определения посмотрим, к какому результату приведет.
Начиная с 7 класса, мы начинаем работать с числами и числовыми выражениями. Начальные определения с переменными переходят к значению выражений с выбранными переменными.
Если имеется выражение с переменными, то оно имеет смысл только тогда, когда при их подстановке значение может быть вычислено.
Если имеется выражение с переменными, то оно не имеет смысл, когда при их подстановке значение не может быть вычислено.
То есть отсюда следует полное определение
Существующими допустимыми переменными называют такие значения, при которых выражение имеет смысл. А если смысла не имеет, значит они считаются недопустимыми.
Для уточнения вышесказанного: если переменных более одной, тогда может быть и пара подходящих значений.
Что такое ОДЗ?
Область допустимых значений – важный элемент при вычислении алгебраических выражений. Поэтому стоит обратить на это внимание при расчетах.
Область ОДЗ – это множество значений, допустимых для данного выражения.
Рассмотрим на примере выражения.
Как найти ОДЗ? Примеры, решения
Найти ОДЗ означает найти все допустимые значения, подходящие для заданной функции или неравенства. При невыполнении этих условий можно получить неверный результат. Для нахождения ОДЗ зачастую необходимо пройти через преобразования в заданном выражении.
Существуют выражения, где их вычисление невозможно:
Все это говорит о том, как важно наличие ОДЗ.
Найти ОДЗ выражения x 3 + 2 · x · y − 4 .
Решение
В куб можно возводить любое число. Данное выражение не имеет дроби, поэтому значения x и у могут быть любыми. То есть ОДЗ – это любое число.
Ответ: x и y – любые значения.
Решение
Видно, что имеется одна дробь, где в знаменателе ноль. Это говорит о том, что при любом значении х мы получим деление на ноль. Значит, можно сделать вывод о том, что это выражение считается неопределенным, то есть не имеет ОДЗ.
Решение
Решение
Почему важно учитывать ОДЗ при проведении преобразований?
При тождественных преобразованиях важно находить ОДЗ. Бывают случаи, когда существование ОДЗ не имеет место. Чтобы понять, имеет ли решение заданное выражение, нужно сравнить ОДЗ переменных исходного выражения и ОДЗ полученного.
Рассмотрим на примере.
Рассмотрим пример с наличием подкоренного выражения.
Нужно избегать преобразований, которые сужают ОДЗ.
Следует придерживаться тождественных преобразований, которые ОДЗ не изменят.
Если имеются примеры, которые его расширяют, тогда его нужно добавлять в ОДЗ.
При наличии логарифмов дело обстоит немного иначе.
При решении всегда необходимо обращать внимание на структуру и вид данного по условию выражения. При правильном нахождении области определения результат будет положительным.
ОДЗ. Модуль. Метод интервалов для неравенств
Зачем при решении примеров мы находим ОДЗ?
Насколько это важно и как правильно находить ОДЗ (на примерах).
Как правильно раскрывать модуль.
Как легко решать нервенства с помощью метода интервалов
Если необходимо увеличить шрифт в Лекциях, зайдите в Настройки своего браузера и измените Масштаб.
§ 1. Вступление (стр.1)
— Как работать над Лекциями
— Понятие о выражении с переменной
— Арифметические выражения
— Алгебраические выражения
— Транцендентные выражения
§ 2. ОДЗ (стр.2)
Развитие чисел
— множество натуральных чисел
— множество целых чисел
— множество рациональных чисел (стр.3)
— множество действительных чисел
— числовая ось
Какие математические действия никогда не выполняются на множестве действительных чисел? (стр.4)
Деление на ноль
Корень четной степени из отрицательного числа
Коротко о комплексных числах (стр.5)
Понятие «неотрицательного» числа
Знаки неравенства строгие и нестрогие
Практическое нахождение ОДЗ
Как находить ОДЗ для транцендентных выражений (стр.6)
§ 3. Объединение и пересечение множеств (стр.7)
§ 4. Модуль числа. Выражение под знаком модуля (стр.8)
Примеры на закрепление понятия «модуль» (стр.9)
§ 5. «Арифметический» корень (стр.10)
Арифметический корень из числа
Арифметический корень из выражения
§ 6. Одночлен и многочлен (стр.11)
Одночлен и многочлен
Выделение полного квадрата из квадратного трехчлена
Координаты вершины параболы (стр.12)
Деление многочлена на одночлен и многочлен без остатка и с остатком (стр.13)
§ 7. Основное свойство дроби (стр.14)
Основное свойство дроби
Как избавиться от иррациональности в знаменателе
§ 8. Переменная величина. Понятие функции (стр.15)
§ 9. «Метод интервалов» для решения неравенств
Описание метода интервалов (стр.16)
Примеры на метод интервалов (стр.17)
Раскрытие модулей на ОДЗ
Раскрытие модулей на ОДЗ
При решении задач с модулями не всегда сразу возникает необходимость в применении метода интервалов или каких-либо других способов избавления от модулей. Иногда бывает достаточно провести анализ ОДЗ, и в результате по крайней мере часть модулей удаётся однозначно раскрыть. Рассмотрим три примера.
Пример №274.
Решить уравнение 
Решение:
Очевидно,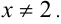 
Более того, так как левая часть уравнения неотрицательна, то и равная ей правая часть должна быть неотрицательна, т.е. 
Но при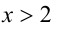 
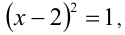
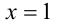
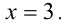
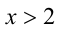
модуль раскрывается положительно, и, решая полученное уравнение 
находим 
или 
Только второе число удовлетворяет условию 
и поэтому будет решением.
Пример №275.
Решить уравнение 
Решение:
Заметим, что левая часть уравнения положительна (как сумма двух неотрицательных слагаемых, одновременно не обращающихся в нуль). Следовательно,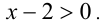 
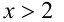
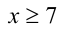
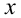
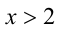
Но при 
оба модуля раскрываются положительно, и, решая полученное неравенство, находим 
. Так как все такие 
удовлетворяют условию , то они являются решениями. Ответ: 
Пример №276.
Решение:
Очевидно,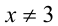
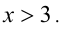
. Более того, так как дробь, по условию, больше 1, то она, как минимум, положительна. При этом числитель дроби положителен, а значит, и знаменатель должен быть положительным, т.е. 
Перепишем неравенство в виде:
Видно, что при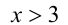 
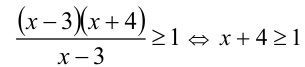
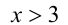
подмодульное выражение положительно, следовательно, модуль однозначно раскрывается, и получаем неравенство 
— верно при. Ответ: 
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института