Как находить смешанное произведение векторов
Смешанное произведение векторов, его свойства, примеры и решения
Для того, чтобы подробно рассмотреть такую тему, нужно охватить еще несколько разделов. Тема напрямую связана с такими терминами, как скалярное и векторное произведение. В этой статье мы постарались дать точное определение, указать формулу, которая поможет определить произведение, используя координаты векторов. Помимо этого, статья включает в себя разделы с перечислением свойств произведения и представлены подробный разбор типовых равенств и задач.
Термин
Для того, чтобы определить, в чем заключается данный термин, нужно взять три вектора.
Умножение в системе координат
Мы можем умножить вектора, если они указаны на координатной плоскости.
Для выполнения скалярного произведения в системе координат необходимо сложить результаты, полученный во время умножения координат.
Мы также можем определить смешанное произведение векторов, если в заданной системе координат указаны координаты векторов, которые умножаются.
Таким образом, можно сделать вывод, что:
Свойства операции над векторами Из особенностей, которые выделяются в скалярном или векторном произведении, можно вывести особенности, которые характеризуют смешанное произведение. Ниже мы приведем основные свойства.
Помимо приведенных свойств, следует уточнить, что если множитель нулевой, то результатом умножения также станет нуль.
Результатом умножения также будет нуль в том случае, если два или больше множителей равны.
Свойства операции умножения чаще всего требуются во время решения задач.
Для того, чтобы подробно разобрать данную тему, возьмем несколько примеров и подробно их распишем.
Для того, чтобы найти решение этого равенства, следует преобразовать его левую часть. Для этого необходимо воспользоваться третьим свойством смешанного произведения, которое гласит:
Необходимо доказать, что модуль смешанного произведения трех векторов не больше, чем произведения их длин.
Решение
Разбор типовых задач
Смешанное произведение также возможно определить с помощью длины вектора, которая уже известна, и угла между ними. Разберем этот тезис в примере.
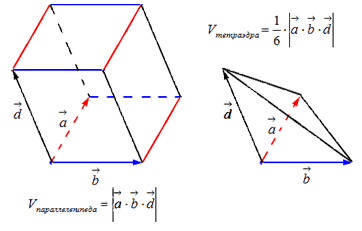
Геометрический смысл
Данная формула и является геометрическим смыслом.
Для того, чтобы закрепить знания, разберем несколько типичных примеров
V п а р а л л е л е п и п и д а = 18