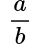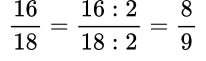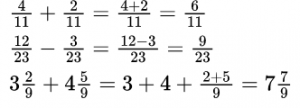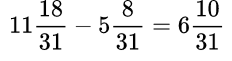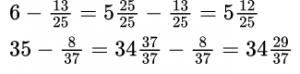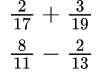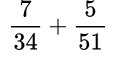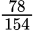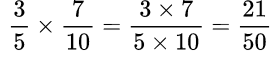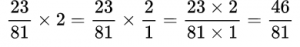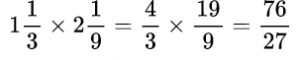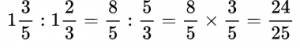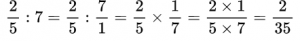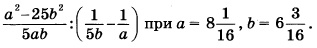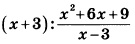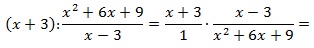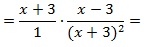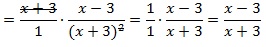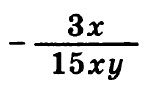Как научиться решать дроби 6 класс
Обыкновенные дроби
теория по математике 📈 числа и вычисления
Обыкновенная дробь – это запись числа в виде:
где число a называют числителем, а число b – знаменателем дроби.
Основное свойство дроби
Если числитель и знаменатель дроби умножить или разделить на одно и то же число, то получится равная ей дробь.
Пример №1. У первой дроби можно разделить числитель и знаменатель на одно и то же число 14, и получится равная ей дробь. Или как у второй дроби можно умножить числитель и знаменатель на одно и то же число, допустим, на 5.
Сократить дробь – значит разделить числитель и знаменатель на одно и то же число.
Пример №2. Чтобы сократить данную дробь надо вспомнить признаки делимости и увидеть, что числитель и знаменатель дроби — четные числа, значит, их можно разделить на 2, то есть дробь сокращается на 2:
Пример №3. По признаку делимости числитель и знаменатель делятся на 5, значит, сокращается данная дробь на 5.
Сложение и вычитание обыкновенных дробей с одинаковыми знаменателями
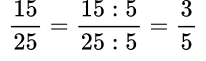
При сложении (вычитании) обыкновенных дробей с одинаковыми знаменателями нужно знаменатель оставить тем же, а числители сложить (вычесть). Если дроби смешанные, то отдельно складывают (вычитают) целые части.
Решения можно записывать короче, выполняя устно сложение или вычитание целых частей, а также – числителей.
Вычитание обыкновенной дроби из целого числа
Чтобы вычесть дробь из единицы, нужно единицу представить в виде неправильной дроби, числитель и знаменатель которой равны знаменателю вычитаемой дроби.
Пример №5. Представляем единицу в виде дроби и получаем вычитание дробей с одинаковыми знаменателями (числители можно вычесть устно).
Вычитание обыкновенной дроби из бóльшего числа
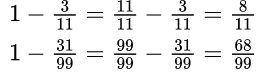
Чтобы вычесть обыкновенную дробь из числа, большего 1, необходимо представить эту дробь в виде смешанного числа, числитель и знаменатель которой равны также знаменателю вычитаемой дроби.
Сложение и вычитание дробей с разными знаменателями
Сложение и вычитание дробей с разными знаменателями требует предварительного приведения дробей к общему знаменателю. Существуют несколько приемов, которыми можно воспользоваться для нахождения общего знаменателя.
Нахождение общего знаменателя
Наименьшее общее кратное (НОК) – это наименьшее число, которое делится без остатка на данные знаменатели одновременно. Обычно его находят устно при выполнении действий с дробями.
Правило нахождения НОК рассмотрим на примере чисел 12 и 15. Пример №7. 1. Нужно разложить на простые множители каждое число:
2. Затем найти одинаковые множители (подчеркиваем):
В данном случае это только множитель 3.
3. Взять одно из данных чисел и домножить на оставшиеся (не подчеркнутые) множители другого числа:
12 домножаем на 5: 12×5=60, или
15 домножаем на 2 и 2: 15×2×2=60
Таким образом, НОК =60. Обычно достаточно просто внимательно посмотреть на числа и в уме подобрать для них НОК.
Перемножение знаменателей. Приём №2.
Нам необходимо просто перемножить знаменатели. Обычно этот прием используется тогда, когда даны простые числа (которые делятся на 1 и на само себя) и на множители их не разложить.
Пример №8. 
Для нахождения общего знаменателя в первом случае: 17×19=323, во втором: перемножаем 11 и 13, получаем 143.
Последовательный подбор. Приём №3.
Данный способ можно применить для небольших чисел устно: возьмем больший из знаменателей, умножим его на 2 и проверим, делится ли это число на второй знаменатель. Если нет, то умножим последовательно на 3, 4 и проверим аналогично.
Пример №9. Возьмем число 51, умножим на 2, получим 102 — видим, что 102 делится на 34, поэтому 102 и будет общий знаменатель.
После того, как мы научились находить общий знаменатель, приступаем непосредственно к алгоритму сложения (или вычитания) обыкновенных дробей с разными знаменателями.
Находим общий знаменатель. Можно использовать прием, когда умножаем 11 и 14, так как 11 — простое число. Следовательно, общий знаменатель равен 154. Находим дополнительный множитель к каждому числителю:
Выполняем умножение в числителе: 
Выполняем сложение дробей с одинаковыми знаменателями: 
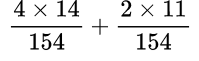
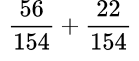
Умножение обыкновенных дробей
При умножении обыкновенных дробей получают дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей.
При умножении обыкновенной дроби и целого числа необходимо целое число представить в виде дроби, числитель которой равен этому числу, а знаменатель равен 1 (что по сути означает перемножение числителя единственной первой дроби и целого числа, знаменатель же остается от первой дроби, так не меняется при умножении на единицу).
Если даны смешанные дроби, то необходимо сначала смешанную дробь перевести в неправильную, а затем выполнить умножение.
Пример №11. Здесь числитель 3 умножили на числитель 7, знаменатель 5 на знаменатель 10.
Пример №12. Случай, когда мы находим произведение дроби и целого числа. Целое число представили в виде дроби со знаменателем 1.
Пример №13. Нам даны смешанные дроби, переводим их в неправильные для выполнения умножения.
Деление обыкновенных дробей
При делении обыкновенных дробей необходимо делимое (то есть первую дробь) умножить на перевернутую вторую дробь, то есть дробь, обратную второй.
Если даны смешанные числа, то перед выполнением деления их необходимо перевести в обыкновенные неправильные дроби.
Если дробь нужно разделить на целое число, то его сначала нужно представить в виде дроби, а затем выполнить деление по правилу.
Пример №14. Делимое умножаем на число, обратное делителю.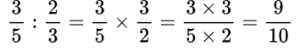 
Пример №15. Смешанные дроби сначала переводим в неправильные, а затем выполняем деление. 
Пример №16. Деление дроби на целое число, где целое число 7 представлено в виде обыкновенной дроби.
Найдите значение выражения:
Упрощение заданного выражения нужно начать с преобразований в скобках. Здесь следует привести дроби к общему знаменателю:
теперь переходим от деления дробей к их умножению: 
затем 1) сокращаем дроби на 5ab; 2) в числителе первой дроби раскладываем выражение, используя формулу сокращенного умножения для разности квадратов:
сокращаем выражение на (a–5b): 
Представим числовые значения для a и b в виде неправильных дробей (для удобства вычислений): 
Подставим полученные значения в выражение и найдем конечный результат: 
Ответ: 39
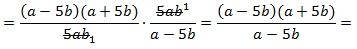
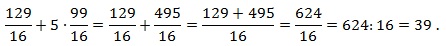
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите значение выражения при x = 12:
Выполним тождественные преобразования выражения, чтобы упростить его. 1-й шаг – переход от деления дробей к их умножению:
далее в знаменателе второй дроби сворачиваем выражение по формуле сокращенного умножения (используем ф-лу для квадрата суммы):
теперь сокращаем выражение (в числителе первой дроби и в знаменателе второй) и приходим к окончательно упрощенному виду:
Подставляем числовое значение для х в полученное выражение и находим результат:
Ответ: 0,6
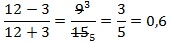
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите значение выражения
В первую очередь в заданиях такого типа необходимо упростить выражение, а затем подставить числа. Приведем выражение к общему знаменателю — это b, для этого умножим первое слагаемое на b, после этого получим в числителе:
Приведем подобные слагаемые — это 9b² и — 9b², в числителе остается 5a. Запишем конечную дробь:
Вычислим её значение, подставив числа из условия:
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите значение выражения:
Итак, в данном задании при вычитании дробей нам необходимо привести их к общему знаменателю. Общий знаменатель — это 15 x y, для этого необходимо первую дробь домножить на 5 y — и числитель и знаменатель, естественно:
Далее, после того как дроби приведены к общему знаменателю, можно производить вычисления. Вычислим числитель:
5 y — (3 x + 5 y) = 5 y — 3 x — 5 y = — 3 x
Тогда дробь примет вид:
Выполнив простые сокращения числителя и знаменателя на 3 и на x, получим: — 1/5 y
Подставим значение y = 0,5: — 1 / (5 • 0,5) = — 1 / 2,5 = — 0,4
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите значение выражения:
В данном случае, в отличие от первого, мы будем упрощать выражение вынося за скобки, а не раскрывая их.
Сразу можно заметить, что b присутствует у первой дроби в числителе, а у второй — в знаменателе, поэтому можем их сократить. Семь и четырнадцать тоже сокращаются на семь:
Далее выносим из числителя второй дроби a:
Подставляем значение a = 13:
pазбирался: Даниил Романович | обсудить разбор | оценить
Какое из данных ниже чисел является значением выражения?
Заметим, что в знаменателе присутствует разность (4 — √14), от которой нам необходимо избавиться. Как же это сделать?
Для этого вспоминаем формулу сокращенного умножения, а именно разность квадратов! Чтобы правильно её применить в этом задании необходимо помнить правила обращения с дробями. В данном случае вспоминаем, что дробь не изменяется, если числитель и знаменатель домножить на одно и то же число или выражение. Для разности квадратов нам не хватает выражения (4 + √14), значит, домножим на него числитель и знаменатель.
После этого в числителе получим 4 + √14, а в знаменателе разность квадратов: 4² — (√14)². После этого знаменатель легко вычисляется:
Суммарно наши действия выглядят так:
pазбирался: Даниил Романович | обсудить разбор | оценить
Аналогично предыдущим заданиям вычисляем знаменатель: для этого приводим дроби к общему знаменателю — это 84. Для этого первую дробь умножаем на 4, а вторую на 3, получим:
1/21 + 1/28 = 4/84 + 3/84
Итак, мы получили в знаменателе 7/84, теперь делим числитель на знаменатель — это все равно что умножить 1 на обратную 7/84 дробь:
1 / ( 7 / 84 ) = 1 •84/7 = 84/7
Далее остается поделить 84 на 7:
pазбирался: Даниил Романович | обсудить разбор | оценить
Можно решать задачу напрямую — вычисляя значения последовательно, это не должно составить труда, однако решение будет долгим и с большими вычислениями. Здесь можно заметить, что 1/3 присутствует как в уменьшаемом — 6 • (1/3)², так и в вычитаемом — 17 • 1/3, поэтому её можно легко вынести за скобку.
Проведя вычисления в скобках, получим:
pазбирался: Даниил Романович | обсудить разбор | оценить
Как решать дроби. Решение дробей.
В статье покажем, как решать дроби на простых понятных примерах. Разберемся, что такое дробь и рассмотрим решение дробей!
Понятие дроби вводится в курс математики начиная с 6 класса средней школы.
В первом случае торт разрезали поровну и взяли одну половину, т.е. 1/2. Во втором случае торт разрезали на 7 частей, из которых взяли 4 части, т.е. 4/7.
Если часть от деления одного числа на другое не является целым числом, ее записывают в виде дроби.
Например, выражение 4:2 = 2 дает целое число, а вот 4:7 нацело не делится, поэтому такое выражение записывается в виде дроби 4/7.
Иными словами дробь — это выражение, которое обозначает деление двух чисел или выражений, и которое записывается с помощью дробной черты.
Например, 5 целых 3/4.
Данная запись означает, что для того, чтобы получить целую 6 не хватает одной части от четырех.
Если вы хотите запомнить, как решать дроби за 6 класс, вам надо понять, что решение дробей, в основном, сводится к понимаю нескольких простых вещей.
Как решать дроби. Примеры.
К дробям применимы самые разные арифметические операции.
Приведение дроби к общему знаменателю
Например, необходимо сравнить дроби 3/4 и 4/5.
Чтобы решить задачу, сначала найдем наименьший общий знаменатель, т.е. наименьшее число, которое делится без остатка на каждый из знаменателей дробей
Наименьший общий знаменатель(4,5) = 20
Затем знаменатель обоих дробей приводится к наименьшему общему знаменателю
Ответ: 15/20 Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
Я вообще не умею решать дроби, но понятие немного есть. И поэтому стараюсь как можно скорее научиться решать дроби как дважды два четыре. Мне легче с формулами сложные примеры решить чем решать дроби!
говорит та самая красотка которая не навидит дроби
Действия с дробями: правила, примеры, решения
Правила выполнения действий с числовыми дробями общего вида
Существуют правила, по которым идет выполнение действий с обыкновенными дробями. Оно подходит и для дробей общего вида:
Обоснование правил
Существуют следующие математические моменты, на которые следует опираться при вычислении:
С их помощью можно производить преобразования вида:
Примеры
В предыдущем пункте было сказано про действия с дробями. Именно после этого дробь нуждается в упрощении. Подробно эта тема была рассмотрена в пункте о преобразовании дробей.
Для начала рассмотрим пример сложения и вычитания дробей с одинаковым знаменателем.
Решение
Имеется другой способ решения. Для начала производится переход к виду обыкновенной дроби, после чего выполняем упрощение. Это выглядит таким образом:
Так как даны равные знаменатели, значит, что мы выполняем вычисление дроби при одинаковом знаменателе. Получим, что
Имеются примеры вычисления дробей с разными знаменателями. Важный пункт – это приведение к общему знаменателю. Без этого мы не сможем выполнять дальнейшие действия с дробями.
Процесс отдаленно напоминает приведение к общему знаменателю. То есть производится поиск наименьшего общего делителя в знаменателе, после чего добавляются недостающие множители к дробям.
Если складываемые дроби не имеют общих множителей, тогда им может стать их произведение.
Решение
2 3 5 + 1 + 1 2 = 2 · 2 2 · 3 5 + 1 + 1 · 3 5 + 1 2 · 3 5 + 1 = = 4 2 · 3 5 + 1 + 3 5 + 1 2 · 3 5 + 1 = 4 + 3 5 + 1 2 · 3 5 + 1 = 5 + 3 5 2 · 3 5 + 1
Ответ: 2 3 5 + 1 + 1 2 = 5 + 3 5 2 · 3 5 + 1
Когда имеем дело с дробями общего вида, тогда о наименьшем общем знаменателе обычно дело не идет. В качестве знаменателя нерентабельно принимать произведение числителей. Для начала необходимо проверить, имеется ли число, которое меньше по значению, чем их произведение.
Рассмотрим примеры умножений дробей общего вида.
Решение
Используя правило перехода от деления к умножению на обратную дробь, получим дробь, обратную данной. Для этого числитель и знаменатель меняются местами. Рассмотрим на примере:
5 · 3 3 2 + 1 : 10 9 3 = 5 · 3 3 2 + 1 · 9 3 10
После чего должны выполнить умножение и упростить полученную дробь. Если необходимо, то избавиться от иррациональности в знаменателе. Получаем, что
Выполнение действие с дробями, содержащими переменные
Примеры сложения и вычитания дробей с переменными
Решение
Рассмотрим двоякий способ решения.
Первый способ заключается в том, что знаменатель первой дроби подвергается разложению на множители при помощи квадратов, причем с ее последующим сокращением. Получим дробь вида
В таком случае необходимо избавляться от иррациональности в знаменателе.
В последнем примере получили, что приведение к общему знаменателю неизбежно. Для этого необходимо упрощать дроби. Для сложения или вычитая всегда необходимо искать общий знаменатель, который выглядит как произведение знаменателей с добавлением дополниетльных множителей к числителям.
Решение
После чего получаем, что
Ответ:
Примеры умножения дробей с переменными
При умножении дробей числитель умножается на числитель, а знаменатель на знаменатель. Тогда можно применять свойство сокращения.
Решение
Необходимо выполнить умножение. Получаем, что
Деление
Возведение в степень
Порядок выполнения действий с дробями
Действия над дробями выполняются по определенным правилам. На практике замечаем, что выражение может содержать несколько дробей или дробных выражений. Тогда необходимо все действия выполнять в строгом порядке: возводить в степень, умножать, делить, после чего складывать и вычитать. При наличии скобок первое действие выполняется именно в них.
Решение
1 + 1 x = 1 1 + 1 x = x x + 1 x = x + 1 x
Тема дроби 6 класс, правильные, неправильные, смешанные. Примеры решения дроби 6 класс. Действия с дробями 6 класс, деление, умножение, сокращение
С дробями ученики знакомятся еще в 5 классе. Раньше людей, которые умели производить действия с дробями, считали очень умными. Первой дробью была 1/2, то есть половина, дальше появились 1/3 и т.д. Несколько веков примеры считались слишком сложными. Сейчас же разработаны подробные правила по преобразованию дробей, сложению, умножению и другим действиям. Достаточно немного разобраться в материале, и решение будет даваться легко.
Повторение обычные дроби 6 класс
Обыкновенная дробь, которую называют простой дробью, записывается как деление двух чисел: m и n.
m — это делимое, то есть числитель дроби, а делитель n называют знаменателем.
Выделяют правильные дроби (m n).
Правильная дробь меньше единицы (к примеру 5/6 — это значит, что от единицы взято 5 частей; 2/8 — от единицы взято 2 части). Неправильная дробь равна или больше 1 (8/7 — единицей будет 7/7 и плюсом взята еще одна часть).
Так, единица, это когда числитель и знаменатель совпали (3/3, 12/12, 100/100 и другие).
Действия с обыкновенными дробями 6 класс
С простыми дробями можно производить следующие действия:
Примеры действий с дробями рассмотрим ниже.
Сокращенные дроби 6 класс
Сократить — значит поделить верхнюю и нижнюю часть дроби на какое-либо одинаковое число.
На рисунке представлены просты примеры сокращения. В первом варианте можно сразу догадаться, что числитель и знаменатель делятся на 2.
На заметку! Если число четное, то оно по-любому делится на 2. Четные числа — это 2, 4, 6…328 (заканчивается на четное) и т. д.
Во втором случае при делении 6 на 18 сразу видно, что числа делятся на 2. Разделив, получаем 3/9. Эта дробь делится еще на 3. Тогда в ответе получается 1/3. Если перемножить оба делителя: 2 на 3, то выйдет 6. Получается, что дробь была разделена на шестерку. Такое постепенное деление называется последовательным сокращением дроби на общие делители.
Кто-то сразу поделит на 6, кому-то понадобится деление частями. Главное, чтобы в конце осталась дробь, которую уже никак не сократить.
Отметим, что если число состоит из цифр, при сложении которых получится число, делящееся на 3, то и первоначальное также можно сократить на 3. Пример: число 341. Складываем цифры: 3 + 4 + 1 = 8 (8 на 3 не делится, значит, число 341 нельзя сократить на 3 без остатка). Другой пример: 264. Складываем: 2 + 6 + 4 = 12 (делится на 3). Получаем: 264 : 3 = 88. Это упростит сокращение больших чисел.
Помимо метода последовательного сокращения дроби на общие делители есть и другие способы.
НОД — это самый большой делитель для числа. Найдя НОД для знаменателя и числителя, можно сразу сократить дробь на нужное число. Поиск осуществляется путем постепенного деления каждого числа. Далее смотрят, какие делители совпадают, если их несколько (как на картинке ниже), то нужно перемножить.
Смешанные дроби 6 класс
Все неправильные дроби можно превратить в смешанные, выделив в них целую часть. Целое число пишется слева.
Часто приходится из неправильной дроби делать смешанное число. Процесс преобразования на примере ниже: 22/4 = 22 делим на 4, получаем 5 целых (5 * 4 = 20). 22 — 20 = 2. Получаем 5 целых и 2/4 (знаменатель не меняется). Поскольку дробь можно сократить, то делим верхнюю и нижнюю часть на 2.
Смешанное число легко превратить в неправильную дробь (это необходимо при делении и умножении дробей). Для этого: целое число умножим на нижнюю часть дроби и прибавим к этому числитель. Готово. Знаменатель не меняется.
Вычисления с дробями 6 класс
Смешанные числа можно складывать. Если знаменатели одинаковые, то сделать это просто: складываем целые части и числители, знаменатель остается на месте.
При сложении чисел с разными знаменателями процесс сложнее. Сначала приводим числа к одному самому маленькому знаменателю (НОЗ).
В примере ниже для чисел 9 и 6 знаменателем будет 18. После этого нужны дополнительные множители. Чтобы их найти, следует 18 разделить на 9, так находится дополнительное число — 2. Его умножаем на числитель 4 получилась дробь 8/18). То же самое делают и со второй дробью. Преобразованные дроби уже складываем (целые числа и числители отдельно, знаменатель не меняем). В примере ответ пришлось преобразовать в правильную дробь (изначально числитель оказался больше знаменателя).
Обратите внимание, что при разности дробей алгоритм действий такой же.
При умножении дробей важно поместить обе под одну черту. Если число смешанное, то превращаем его в простую дробь. Далее умножаем верхнюю и нижнюю части и записываем ответ. Если видно, что дроби можно сократить, то сокращаем сразу.
В указанном примере сокращать ничего не пришлось, просто записали ответ и выделили целую часть.
В этом примере пришлось сократить числа под одной чертой. Хотя сокращать можно и готовый ответ.
При делении алгоритм почти такой же. Сначала превращаем смешанную дробь в неправильную, затем записываем числа под одной чертой, заменив деление умножением. Не забываем верхнюю и нижнюю часть второй дроби поменять местами (это правило деления дробей).
При необходимости сокращаем числа (в примере ниже сократили на пятерку и двойку). Неправильную дробь преобразуем, выделив целую часть.
Основные задачи на дроби 6 класс
На видео показано еще несколько задач. Для наглядности использованы графические изображения решений, которые помогут наглядно представить дроби.
Примеры умножения дроби 6 класс с пояснениями
Перемножающиеся дроби записываются под одной линией. После этого их сокращают путем деления на одни и те же числа (например, 15 в знаменателе и 5 в числителе можно разделить на пятерку).
Сравнение дробей 6 класс
Чтобы сравнить дроби, нужно запомнить два простых правила.
Правило 1. Если знаменатели разные
Правило 2. Когда знаменатели одинаковые
Например, сравним дроби 7/12 и 2/3.
В качестве тренировки можно выполнить следующие задания.
Сложение дробей 6 класс с разными знаменателями
Совет: если сложно найти наименьший общий знаменатель у дробей (особенно, если значения их небольшие), то можно перемножить знаменатель первой и второй дроби. Пример: 2/8 и 5/9. Найти их знаменатель просто: 8 умножаем на 9, получится 72.
Решение уравнений с дробями 6 класс
В решении уравнений требуется вспомнить действия с дробями: умножение, деление, вычитание и сложение. Если неизвестен один из множителей, то произведение (итог) делится на известный множитель, то есть дроби перемножаются (вторая переворачивается).
Если неизвестно делимое, то знаменатель умножается на делитель, а для поиска делителя нужно делимое разделить на частное.
Представим простые примеры решения уравнений:
Здесь требуется лишь произвести разность дробей, не приводя к общему знаменателю.
На видео представлено решение более сложных уравнений.
Многоэтажные дроби 6 класс примеры с пояснениями
Многоэтажной дробью называют дробь, записанную в несколько строк. Пример решения многоэтажной дроби:
Как решали пример способом 1:
Ответ получился в виде неправильной дроби. Ее можно преобразовать в 2 целых и 1/2.
Во втором способе числитель и знаменатель умножили на 4, чтобы сократить нижнюю часть, а не переворачивать знаменатель.
Об Авторе
Смотрите также
Сценарий новогодний Деда Мороза и Снегурочки дома, Новый год семьей с детьми дома: игры с Дедом Морозом и Снегурочкой, загадки, хороводы, подарки. Новый год папа Дед Мороз, слова деда Мороза и Снегурочки в стихах: весело и дружно встретим Новый год
Короткие новогодние сценки для детей: веселые игры для детей на Новый год, смешные новогодние сценки по ролям, короткие сказки сценки для детского сада, начальной школы, ученикам 6 7 класса
Тест Гоголь ночь перед Рождеством 5 класс. Вечера на хуторе близ Диканьки повесть Гоголя 5 класс: пересказ, краткое содержание, жанр произведения, суть повести, главные герои, цитаты
4 комментария
Отличная статья, ставлю пятерку.
Имея высшее техническое образование и помогая внучке в шестом классе я с удовольствием узнал, что внучка и без меня хорошо в дробях разбирается, а я уже и подзабыл НОК. Спасибо.
Как у вас в последнем примере из 5/2 получилось 1 целая 3/5? Будет же 2 целых 1/2
большое спасибо, примите наши извинения за досадную ошибку