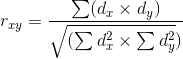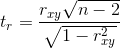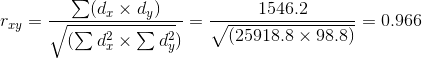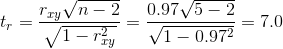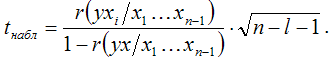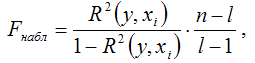какой критерий используют для оценки значимости коэффициента корреляции
Пример. Значимость коэффициента корреляции
Линейное уравнение регрессии имеет вид y=ax+b
1. Параметры уравнения регрессии.
Средние значения
Дисперсия
Среднеквадратическое отклонение
Коэффициент корреляции
Связь между признаком Y фактором X сильная и прямая.
Уравнение регрессии
| x | y | x 2 | y 2 | x·y | y(x) | (y- y ) 2 | (y-y(x)) 2 | (x-x p ) 2 |
| 1 | 0.4 | 1 | 0.16 | 0.4 | 0.4357 | 0.2359 | 0.0013 | 9 |
| 2 | 0.6 | 4 | 0.36 | 1.2 | 0.5857 | 0.0816 | 0.0002 | 4 |
| 3 | 0.7 | 9 | 0.49 | 2.1 | 0.7357 | 0.0345 | 0.0013 | 1 |
| 4 | 0.9 | 16 | 0.81 | 3.6 | 0.8857 | 0.0002 | 0.0002 | 0 |
| 5 | 1.1 | 25 | 1.21 | 5.5 | 1.0357 | 0.0459 | 0.0041 | 1 |
| 6 | 1.3 | 36 | 1.69 | 7.8 | 1.1857 | 0.1716 | 0.0131 | 4 |
| 7 | 1.2 | 49 | 1.44 | 8.4 | 1.3357 | 0.0988 | 0.0184 | 9 |
| 28 | 6.2 | 140 | 6.16 | 29 | 6.2 | 0.6686 | 0.0386 | 28 |
2. Оценка параметров уравнения регрессии.
Значимость коэффициента корреляции определяется по формуле (см. п. VI):
Библиотека постов MEDSTATISTIC об анализе медицинских данных
Ещё больше полезной информации в нашем блоге в Инстаграм @medstatistic
Критерии и методы
КРИТЕРИЙ КОРРЕЛЯЦИИ ПИРСОНА
– это метод параметрической статистики, позволяющий определить наличие или отсутствие линейной связи между двумя количественными показателями, а также оценить ее тесноту и статистическую значимость. Другими словами, критерий корреляции Пирсона позволяет определить, изменяется ли (возрастает или уменьшается) один показатель в ответ на изменения другого? В статистических расчетах и выводах коэффициент корреляции обычно обозначается как rxy или Rxy.
1. История разработки критерия корреляции
Критерий корреляции Пирсона был разработан командой британских ученых во главе с Карлом Пирсоном (1857-1936) в 90-х годах 19-го века, для упрощения анализа ковариации двух случайных величин. Помимо Карла Пирсона над критерием корреляции Пирсона работали также Фрэнсис Эджуорт и Рафаэль Уэлдон.
2. Для чего используется критерий корреляции Пирсона?
Критерий корреляции Пирсона позволяет определить, какова теснота (или сила) корреляционной связи между двумя показателями, измеренными в количественной шкале. При помощи дополнительных расчетов можно также определить, насколько статистически значима выявленная связь.
Например, при помощи критерия корреляции Пирсона можно ответить на вопрос о наличии связи между температурой тела и содержанием лейкоцитов в крови при острых респираторных инфекциях, между ростом и весом пациента, между содержанием в питьевой воде фтора и заболеваемостью населения кариесом.
3. Условия и ограничения применения критерия хи-квадрат Пирсона
Например, рост ребенка зависит от его возраста, то есть чем старше ребенок, тем он выше. Если мы возьмем двух детей разного возраста, то с высокой долей вероятности рост старшего ребенка будет больше, чем у младшего. Данное явление и называется зависимостью, подразумевающей причинно-следственную связь между показателями. Разумеется, между ними имеется и корреляционная связь, означающая, что изменения одного показателя сопровождаются изменениями другого показателя.
В другой ситуации рассмотрим связь роста ребенка и частоты сердечных сокращений (ЧСС). Как известно, обе эти величины напрямую зависят от возраста, поэтому в большинстве случаев дети большего роста (а значит и более старшего возраста) будут иметь меньшие значения ЧСС. То есть, корреляционная связь будет наблюдаться и может иметь достаточно высокую тесноту. Однако, если мы возьмем детей одного возраста, но разного роста, то, скорее всего, ЧСС у них будет различаться несущественно, в связи с чем можно сделать вывод о независимости ЧСС от роста.
Приведенный пример показывает, как важно различать фундаментальные в статистике понятия связи и зависимости показателей для построения верных выводов.
4. Как рассчитать коэффициента корреляции Пирсона?
Расчет коэффициента корреляции Пирсона производится по следующей формуле:
5. Как интерпретировать значение коэффициента корреляции Пирсона?
Более точную оценку силы корреляционной связи можно получить, если воспользоваться таблицей Чеддока:
| Абсолютное значение rxy | Теснота (сила) корреляционной связи |
| менее 0.3 | слабая |
| от 0.3 до 0.5 | умеренная |
| от 0.5 до 0.7 | заметная |
| от 0.7 до 0.9 | высокая |
| более 0.9 | весьма высокая |
Оценка статистической значимости коэффициента корреляции rxy осуществляется при помощи t-критерия, рассчитываемого по следующей формуле:
Полученное значение tr сравнивается с критическим значением при определенном уровне значимости и числе степеней свободы n-2. Если tr превышает tкрит, то делается вывод о статистической значимости выявленной корреляционной связи.
6. Пример расчета коэффициента корреляции Пирсона
Целью исследования явилось выявление, определение тесноты и статистической значимости корреляционной связи между двумя количественными показателями: уровнем тестостерона в крови (X) и процентом мышечной массы в теле (Y). Исходные данные для выборки, состоящей из 5 исследуемых (n = 5), сведены в таблице:
Σ(X) = 951 + 874 + 957 + 1084 + 903 = 4769
Σ(Y) = 83 + 76 + 84 + 89 + 79 = 441
Mx = Σ(X) / n = 4769 / 5 = 953.8
My = Σ(Y) / n = 441 / 5 = 82.2
Корреляционный анализ
Корреляционный анализ
Корреляционный анализ – раздел математической статистики, исследующий зависимости между двумя или более случайными величинами. Термин «Correlation» означает взаимосвязь, взаимоотношение.
Функциональная зависимость и корреляция
Еще Гиппократ обратил внимание на то, что между телосложением и темпераментом людей, между строением их тела и предрасположенностью к заболеваниям существует определенная взаимосвязь.
В области физической культуры и спорта можно привести много примеров такой взаимосвязи. Например, от уровня силы во многом зависит результат, показанный спортсменом в таких видах спорта, как тяжелая атлетика, пауэрлифтинг, гиревой спорт, метание диска и толкание ядра и т.д. Результат в беге на 100 м во многом зависит от процента содержания в мышцах спортсменов быстрых мышечных волокон (II типа). Доказано, что у выдающихся спринтеров этот показатель превышает 80%. Чтобы определить, насколько сильна взаимосвязь между переменными (признаками) используется корреляционный анализ.
Две случайные величины X и Y могут быть:
В качестве меры связи между случайными величинами используется коэффициент корреляции. Коэффициент корреляции для генеральной совокупности обозначается ρ. Однако, как правило, он неизвестен. Поэтому он оценивается по экспериментальным данным, представляющим выборку объема n, полученную при совместном измерении двух переменных (признаков) X и Y. Коэффициент корреляции, определяемый по выборочным данным называется выборочным коэффициентом корреляции (или просто коэффициентом корреляции). Его принято обозначать символом r. Наиболее часто в качестве оценок генерального коэффициента корреляции используется коэффициент корреляции Пирсона (r) и коэффициент корреляции Спирмена (rs).
Коэффициент корреляции Пирсона ( r )
Чтобы правильно применять корреляционный анализ в научных исследованиях, нужно учитывать условия применения этого метода.
Условия, при которых возможен расчет коэффициента корреляции Пирсона:
Коэффициент корреляции Спирмена ( r S)
При расчете коэффициента корреляции Спирмена требования к исходным данным менее строгие, а именно:
Свойства оценок коэффициентов корреляции
| n | 0,05 | 0,01 | 0,001 |
| 3 | 0,9969 | 0,999877 | 0,99999877 |
| 4 | 0,950 | 0,9900 | 0,9990 |
| 5 | 0,878 | 0,9597 | 0,99114 |
| 6 | 0,811 | 0,9172 | 0,9741 |
| 7 | 0,754 | 0,875 | 0,9509 |
| 8 | 0,707 | 0,834 | 0,9244 |
| 9 | 0,666 | 0,798 | 0,898 |
| 10 | 0,632 | 0,765 | 0,872 |
| 20 | 0,444 | 0,561 | 0,679 |
| 30 | 0,361 | 0,463 | 0,570 |
| 40 | 0,312 | 0,402 | 0,501 |
| 50 | 0,279 | 0,361 | 0,451 |
В итоговой таблице необходимо указать объем выборки, чтобы читающий мог оценить значимость (достоверность) вычисленных коэффициентов корреляции. Иногда в публикациях приводятся только значимые коэффициенты корреляции, а вместо незначимых ставится прочерк. В таблице 2 авторы указали, что объем выборки равен n = 32. Критическое значение коэффициента корреляции при n = 32 и a = 0,05 составляет r0,05 = 0,349 (В.С.Иванов, 1990). Следовательно, все коэффициенты корреляции достоверны.
Таблица 2 — Значения коэффициентов корреляции между результатами в скоростно-силовых тестах и результатом в толкании ядра с разгоном n=32, спортивный результат группы варьировал от 12,00 м до 20,50. Критическое значение коэффициента корреляции при n = 32 и a = 0,05 составляет r0,05 = 0,349 (по: Я.Е.Ланка, Ан.А.Шалманов, 1982).
Значимость коэффициента корреляции, доверительный интервал
Проверка гипотезы для коэффициента корреляции
Пусть r обозначает выборочный коэффициент корреляции, полученный по извлеченным из двумерного нормального распределения пар наблюдений (x1, y1),…,(xn, yn).
Коэффициент корреляции 
(1)
где оценки среднего равны:

Проверим значимость коэффициента корреляции.
Очевидно, достаточно большое по абсолютной величине значение величины r будет стремиться опровергнуть нулевую гипотезу.
Насколько большое должно быть абсолютное значение величины r?
Для того чтобы проверить гипотезу, мы должны знать распределение величины r.
Собственное распределение величины r довольно сложное, поэтому мы применим преобразование:

Итак, выборочное распределение этой статистики есть распределение Стьюдента с n-2 степенями свободы.
При заданном уровне значимости (α) определяем критическое значение tкр.
Принимаем решение об отклонении или не отклонении нулевой гипотезы:


Вычисление уровня значимости коэффициента корреляции
Для определения фактического уровня значимости коэффициента корреляции запишем:
Где Т подчиняется распределению Стьюдента с n-2 степенями свободы, а значение величины t вычисляется в соответствии с формулой (2).
Вычисление уровня значимости эквивалентно определению площади под правым и левым хвостами функции, ограниченной значениями -t и t.
Построение доверительного интервала для коэффициента корреляции
Распределение выборочного коэффициента корреляции сложное, поэтому часто пользуются преобразованием Фишера для аппроксимации точного распределения коэффициента корреляции.
При больших значениях n распределение выборочного коэффициента корреляции r стремится к нормальному z.
Для преобразованного z стандартная ошибка среднего равна
Таким образом, двусторонний доверительный интервал для z будет определяться:
Нижняя граница:
Верхняя граница:
Для 

Для построения доверительного интервала для коэффициента корреляции сделаем обратное преобразование, получим:
Проверка гипотезы о значимости частного и множественного коэффициентов корреляции
Предположим, что по данным выборочной совокупности была построена линейная модель множественной регрессии. Задача состоит в проверке значимости частных и множественного коэффициентов корреляции.
Рассмотрим процесс проверки значимости частных коэффициентов корреляции.
Основная гипотеза состоит в предположении о незначимости частных коэффициентов корреляции, т. е.
Обратная или конкурирующая гипотеза состоит в предположении о значимости частных коэффициентов корреляции, т.е.
Данные гипотезы проверяются с помощью t-критерия Стьюдента.
Наблюдаемое значение t-критерия (вычисленное на основе выборочных данных) сравнивают со значением t-критерия, которое определяется по таблице распределения Стьюдента и называется критическим.
При проверке значимости частного коэффициента корреляции критическое значение t-критерия определяется как tкрит( ;n–l–1), где а – уровень значимости, n – объём выборочной совокупности, l – число оцениваемых по выборке параметров, (n–l–1) – число степеней свободы, которое определяется по таблице распределений t-критерия Стьюдента.
При проверке основной гипотезы вида Н0:r(yxi/x1…xn-1)=0 наблюдаемое значение t-критерия Стьюдента рассчитывается по формуле:
При проверке основной гипотезы возможны следующие ситуации.
Если наблюдаемое значение t-критерия (вычисленное по выборочным данным) по модулю больше критического значения t-критерия (определённого по таблице распределения Стьюдента), т. е. |tнабл|›tкрит, то с вероятностью а основная гипотеза о незначимости частного коэффициента корреляции отвергается, и между переменными xi и y существует корреляционная связь при постоянных значениях остальных переменных, включённых в модель регрессии.
Если наблюдаемое значение t-критерия (вычисленное по выборочным данным) по модулю меньше или равно критического значения t-критерия (определённого по таблице распределения Стьюдента), т. е. |tнабл|≤tкрит, то основная гипотеза о незначимости частного коэффициента корреляции принимается, и между переменными xi и y отсутствует корреляционная связь при постоянных значениях остальных переменных, включённых в модель регрессии. Следовательно, включение независимой переменной xi в данную модель регрессии является необоснованным.
Рассмотрим процесс проверки значимости коэффициента множественной корреляции.
Основная гипотеза состоит в предположении о незначимости коэффициента множественной корреляции, т. е.
Обратная или конкурирующая гипотеза состоит в предположении о значимости коэффициента множественной корреляции, т. е.
Данные гипотезы проверяются с помощью F-критерия Фишера-Снедекора через коэффициент множественной детерминации.
Наблюдаемое значение F-критерия (вычисленное на основе выборочных данных) сравнивают со значением F-критерия, которое определяется по таблице распределения Фишера-Снедекора, и называется критическим.
При проверке значимости коэффициента множественной корреляции критическое значение F-критерия определяется как Fкрит(a;k1;k2), где а – уровень значимости, k1=l–1 и k2=n–l – число степеней свободы, n – объём выборочной совокупности, l – число оцениваемых по выборке параметров.
При проверке основной гипотезы вида Н0:R(y,xi)=0 наблюдаемое значение F-критерия Фишера-Снедекора рассчитывается по формуле:
где R 2 (y,xi) – коэффициент множественный детерминации.
При проверке основной гипотезы возможны следующие ситуации.
Если наблюдаемое значение F-критерия (вычисленное по выборочным данным) больше критического значения F-критерия (определённого по таблице распределения Фишера-Снедекора), т. е. Fнабл>Fкрит, то с вероятностью а основная гипотеза о незначимости коэффициента множественной корреляции отвергается, и он признаётся значимым. В этой ситуации включение в модель регрессии всех исследуемых переменных считается обоснованным.
Если наблюдаемое значение F-критерия (вычисленное по выборочным данным) меньше или равно критического значения F-критерия (определённого по таблице распределения Фишера-Снедекора), т. е. Fнабл≤Fкрит, то основная гипотеза о незначимости коэффициента множественной корреляции принимается, и он признаётся незначимым. В этой ситуации построение модели регрессии на основе исследуемых переменных считается необоснованным.